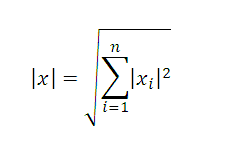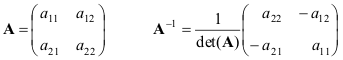Как найти нормированные векторы

Была ли эта статья полезной?

Нежное введение в векторные нормы в машинном обучении

Дата публикации 2018-02-05

Вычисление длины или величины векторов часто требуется либо непосредственно как метод регуляризации в машинном обучении, либо как часть более широких векторных или матричных операций.

В этом уроке вы узнаете, как рассчитать длину или величину вектора, называемую векторной нормой.

После завершения этого урока вы узнаете:

• Норма L1, которая рассчитывается как сумма абсолютных значений вектора.
• Норма L2, которая рассчитывается как квадратный корень из суммы квадратов векторных значений.
• Максимальная норма, которая рассчитывается как максимальные значения вектора.

• Обновление март / 2018: Исправлена ​​опечатка в уравнении максимальной нормы.
• Обновление сентябрь / 2018: Исправлена ​​опечатка, связанная с размером заданных векторов.

Обзор учебника

Этот урок разделен на 4 части; они есть:

1. Вектор Норма
2. Вектор L1 Норма
3. Вектор L2 Норма
4. Вектор Макс Норм

Вектор Норма

Вычисление размера или длины вектора часто требуется либо непосредственно, либо как часть более широкой операции над вектором или векторной матрицей.

Длина вектора называется векторной нормой или величиной вектора.

Длина вектора представляет собой неотрицательное число, которое описывает экстент вектора в пространстве, и иногда его называют величиной или нормой вектора.

Длина вектора всегда является положительным числом, за исключением вектора со всеми нулевыми значениями. Он рассчитывается с использованием некоторой меры, которая суммирует расстояние вектора от начала векторного пространства. Например, источником векторного пространства для вектора с 3 элементами является (0, 0, 0).

Обозначения используются для представления векторной нормы в более широких вычислениях, а тип вычисления векторной нормы почти всегда имеет свои собственные уникальные обозначения.

Мы рассмотрим несколько общих вычислений векторной нормы, используемых в машинном обучении.

Вектор L1 Норма

Длина вектора может быть вычислена с использованием нормы L1, где 1 – верхний индекс L, например, L ^ 1.

Обозначения для нормы L1 вектора: || v || 1, где 1 – индекс. Таким образом, эту длину иногда называют нормой такси или нормой Манхэттена.

Норма L1 рассчитывается как сумма абсолютных значений вектора, где абсолютное значение скаляра использует обозначение | a1 |. По сути, норма – это вычисление манхэттенского расстояния от начала векторного пространства.

Норма L1 вектора может быть вычислена в NumPy с помощью функции norm () с параметром для указания порядка нормы, в данном случае 1.

Сначала определяется вектор 1 × 3, затем вычисляется норма вектора L1.

При выполнении примера сначала печатается определенный вектор, а затем норма L1 вектора.

Норма L1 часто используется при подборе алгоритмов машинного обучения в качестве метода регуляризации, например метод, позволяющий сохранять коэффициенты модели малыми, и, в свою очередь, модель менее сложной.

Вектор L2 Норма

Длина вектора может быть вычислена с использованием нормы L2, где 2 – верхний индекс L, например, L ^ 2.

Обозначения для L2-нормы вектора: || v || 2, где 2 – индекс.

Норма L2 вычисляет расстояние векторной координаты от начала векторного пространства. Как таковая, она также известна как евклидова норма, поскольку она рассчитывается как евклидово расстояние от начала координат. Результатом является положительное значение расстояния.

Норма L2 рассчитывается как квадратный корень из суммы квадратов векторных значений.

Норму L2 вектора можно рассчитать в NumPy с помощью функции norm () с параметрами по умолчанию.

Сначала определяется вектор 1 × 3, затем вычисляется норма вектора L2.

При выполнении примера сначала печатается определенный вектор, а затем норма L2 вектора.

Как и норма L1, норма L2 часто используется при подборе алгоритмов машинного обучения в качестве метода регуляризации, например метод, позволяющий сохранять коэффициенты модели малыми и, в свою очередь, модель менее сложной.

Безусловно, норма L2 чаще используется, чем другие векторные нормы в машинном обучении.

Вектор Макс Норм

Длина вектора может быть рассчитана с использованием максимальной нормы, также называемой максимальной нормой.

Максимальная норма вектора называется L ^ inf, где inf – верхний индекс и может быть представлен символом бесконечности. Обозначения для максимальной нормы: || x || inf, где inf – индекс.

Максимальная норма вычисляется как возвращающая максимальное значение вектора, отсюда и название.

Максимальная норма вектора может быть вычислена в NumPy с помощью функции norm () с параметром порядка, установленным в inf.

Сначала определяется вектор 1 × 3, затем вычисляется максимальная норма вектора.

При запуске примера сначала печатается определенный вектор, а затем максимальная норма вектора

Максимальная норма также используется в качестве регуляризации в машинном обучении, например, в весах нейронных сетей, называемой максимальной нормализацией.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Создайте 5 примеров, используя каждую операцию, используя ваши собственные данные.
• Реализуйте каждую матричную операцию вручную для матриц, определенных как списки списков.
• Найдите документы по машинному обучению и найдите 1 пример каждой используемой операции.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

• Введение в линейную алгебру, 2016
• Глава 2, Линейная алгебра,Глубокое обучение, 2016

статьи

Резюме

В этом уроке вы обнаружили различные способы вычисления длины или величины вектора, называемые векторной нормой.

В частности, вы узнали:

• Норма L1, которая рассчитывается как сумма абсолютных значений вектора.
• Норма L2, которая рассчитывается как квадратный корень из суммы квадратов векторных значений.
• Максимальная норма, которая рассчитывается как максимальные значения вектора.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Нормальный вектор прямой, координаты нормального вектора прямой

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

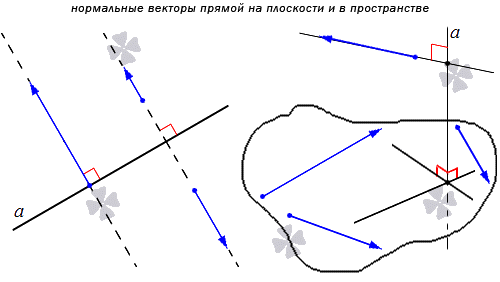
Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.

Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .

Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Задана прямая вида 2 x + 7 y – 4 = 0 _, найти координаты нормального вектора.

По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Указать нормальный вектор для заданной прямой y – 3 = 0 .

По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y – 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .

Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.

Найти координаты нормального вектора, если дано уравнение прямой x 1 3 – y = 1 .

Для начала необходимо перейти от уравнения в отрезках x 1 3 – y = 1 к уравнению общего вида. Тогда получим, что x 1 3 – y = 1 ⇔ 3 · x – 1 · y – 1 = 0 .

Отсюда видно, что координаты нормального вектора имеют значение 3 , – 1 .

Ответ: 3 , – 1 .

Если прямая определена каноническим уравнением прямой на плоскости x – x 1 a x = y – y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x – x 1 a x = y – y 1 a y ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0

Для решения можно выбирать любой удобный способ.

Найти нормальный вектор заданной прямой x – 2 7 = y + 3 – 2 .

Из прямой x – 2 7 = y + 3 – 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , – 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , – 2 ) .

Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , – 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x – 2 · n y = 0 .

Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 – 2 · n y = 0 ⇔ n y = 7 2 .

Значит, нормальный вектор имеет координаты 1 , 7 2 .

Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем

x – 2 7 = y + 3 – 2 ⇔ 7 · ( y + 3 ) = – 2 · ( x – 2 ) ⇔ 2 x + 7 y – 4 + 7 3 = 0

Полученный результат координат нормального вектора равен 2 , 7 .

Ответ: 2 , 7 или 1 , 7 2 .

Указать координаты нормального вектора прямой x = 1 y = 2 – 3 · λ .

Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:

x = 1 y = 2 – 3 · λ ⇔ x = 1 + 0 · λ y = 2 – 3 · λ ⇔ λ = x – 1 0 λ = y – 2 – 3 ⇔ x – 1 0 = y – 2 – 3 ⇔ ⇔ – 3 · ( x – 1 ) = 0 · ( y – 2 ) ⇔ – 3 · x + 0 · y + 3 = 0

Отсюда видно, что координаты нормального вектора равны – 3 , 0 .

Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .

Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .

Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x – x 1 a x = y – y 1 a y = z – z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .

Линейная алгебра для разработчиков игр

Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.

Зачем нам линейная алгебра?

Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.

Что такое вектор?

В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора: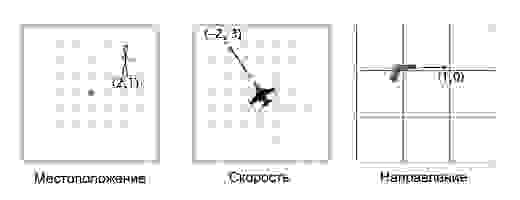

Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.

Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).

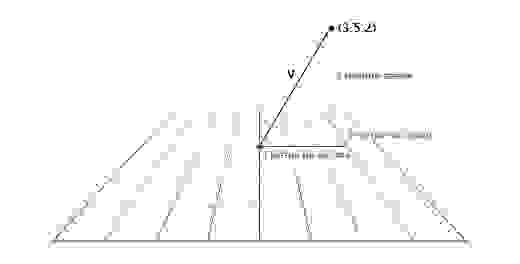
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.

Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.

Сложение векторов

Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:

(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)

Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.

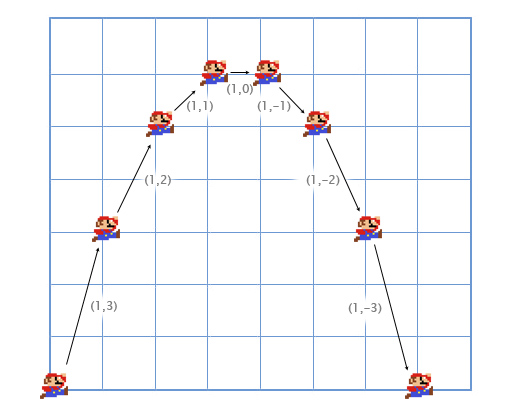
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.

Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.

Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).

Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).

Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.

Вычитание векторов

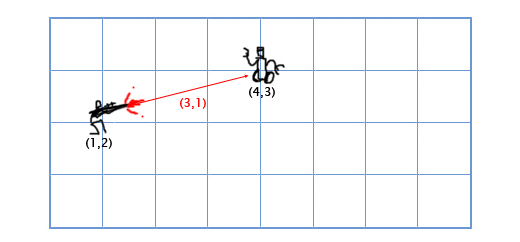
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:

(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).

Умножение вектора на скаляр

Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:

0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).

Длина вектора

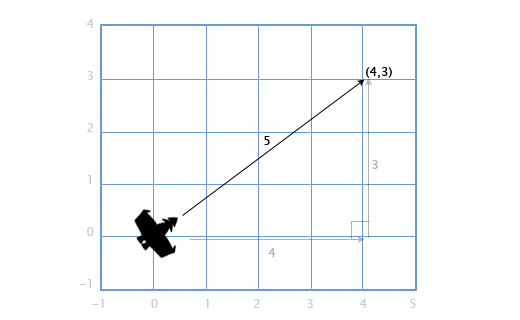
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.

Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2

В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).

Итак, скорость нашего корабля равна:

|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5

Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )

Расстояние

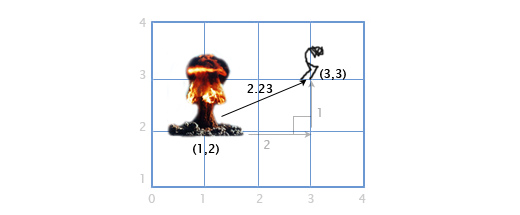
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.

Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23

Нормализация

Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?

Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.

Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:

(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1

Скалярное произведение векторов

Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе

(a1, a2) • (b1, b2) = a1b1 + a2b2

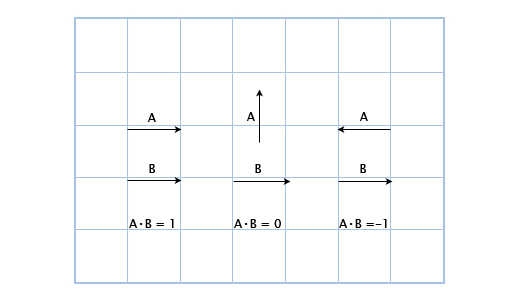
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:

Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.

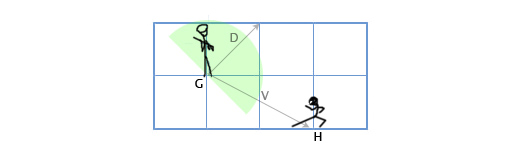
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:

V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1

Так как единица больше нуля, то главный герой находится в поле зрения стражника.

Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:

Где Θ (произносится как «theta») — угол между векторами A и B.

Это позволяет нам найти Θ (угол) с помощью выражения:

Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:

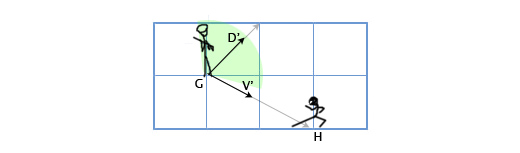
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.

D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)

Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72

Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.

Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:

Векторное произведение

Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?

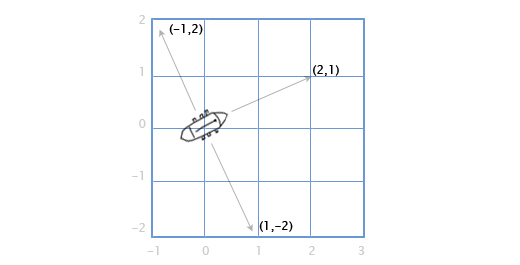
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).

А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
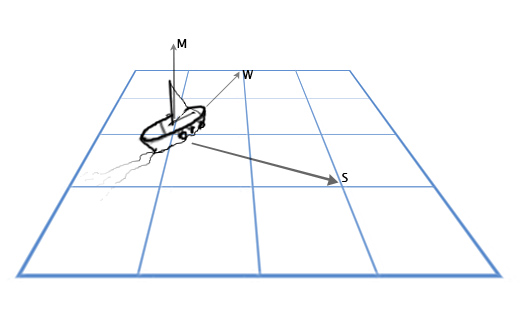
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».

Для решения этой задачи мы используем векторное произведение: S = M x W.

Подставим теперь нужные нам значения:

S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)

Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.

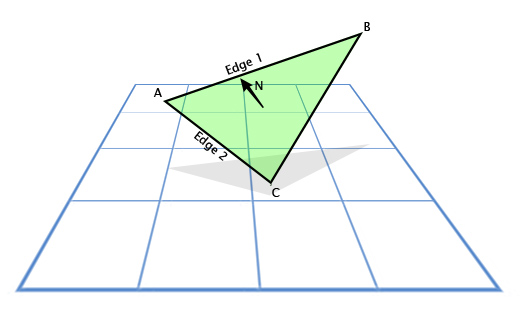
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.

Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».

Вот так это выглядит в коде:

В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.

Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).

Для начала изучим «строительные блоки» матрицы преобразований.

Базисный вектор

Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:

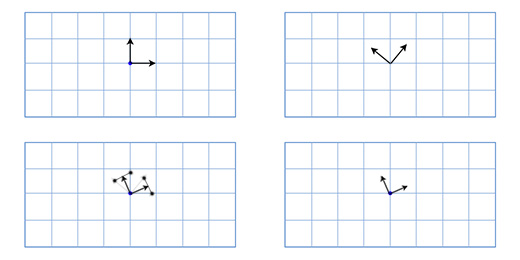
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:

Применяя эту функцию ко всем трём точкам, мы получим следующую картину:

Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).

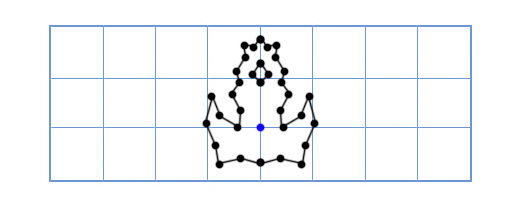
Пусть теперь наш корабль выглядит вот так:

Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»

Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.

По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.

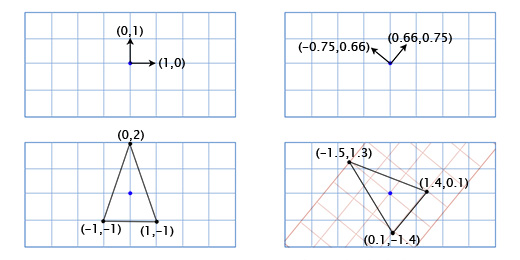
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:

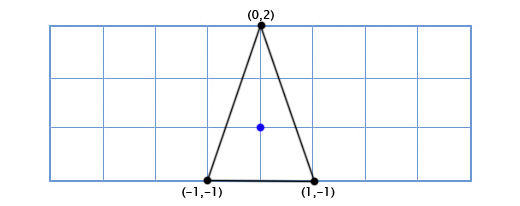
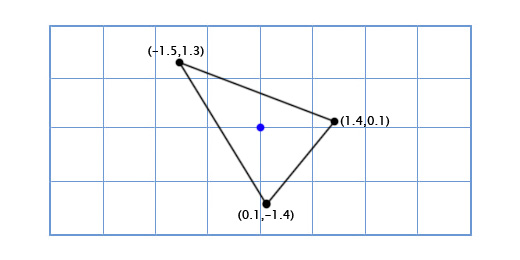
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:

0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)

Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:

-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)

Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y

1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)

Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.

Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:

Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.

Матрицы

Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:

Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:

Будучи записанным по-другому, это выражение выглядит так:

Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:

Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:

Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:

Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.

К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:

И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:

Теперь, когда мы перемножаем их, мы получаем:

(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)

Что, в свою очередь, может быть записано как:

x(a, b) + y(c, d) + (e, f)

Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.

Трехмерные матрицы

Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:

Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:

И добавляем единицу [1] в вектор, как здесь:

Вращение в двухмерном пространстве

Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:

Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:

(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))

Затем, мы включаем координатную ось Y (0, 1). Получим:

(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))

Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:

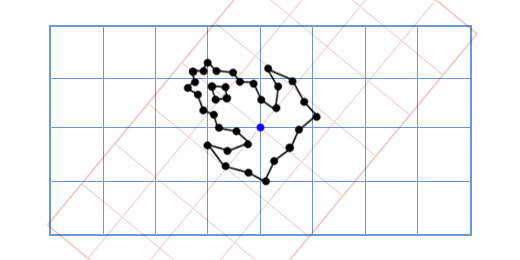
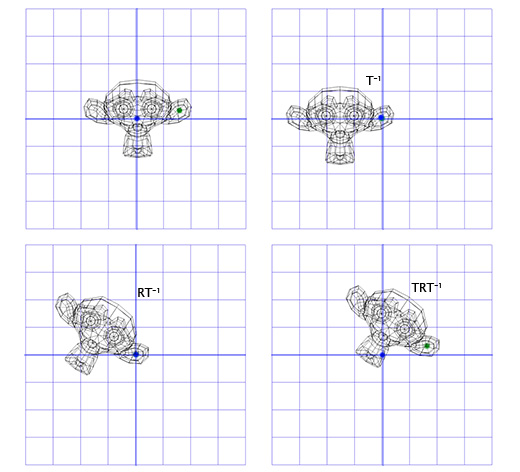
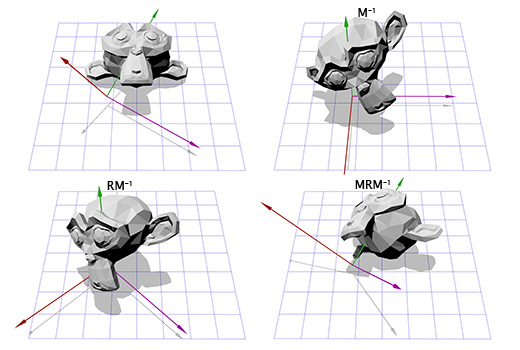
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.

Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:

Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:

Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.

Теперь рассмотрим трёхмерное вращение.

Трёхмерное вращение

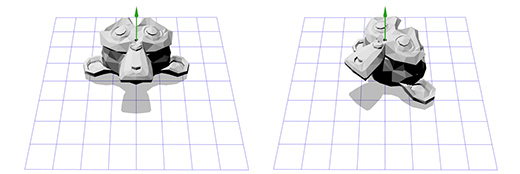
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:

Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.

То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?

Вращение, определяемое осью и углом (Axis-angle rotation)

Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.

Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?

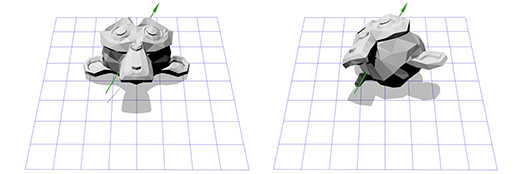
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:

Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.

Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.

У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.

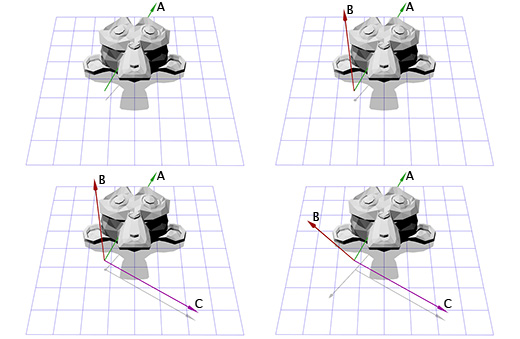
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.

На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:

Тут показана иллюстрация для каждого шага:

Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.

Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.

Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.

Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.

Эйлеровские углы

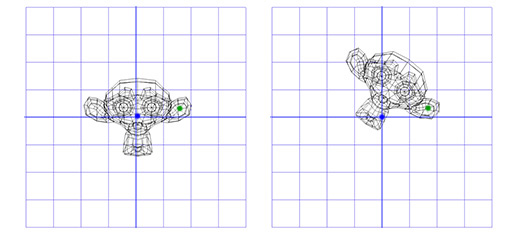
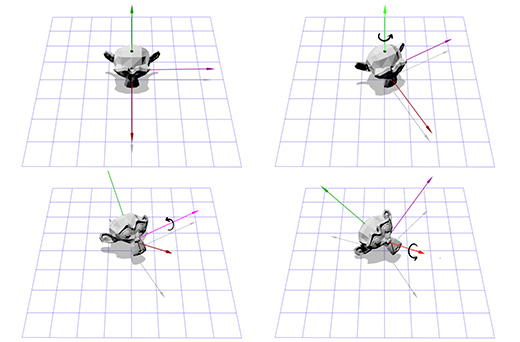
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.

Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).

Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.

Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.

Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.

Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?

Вращение с помощью матриц

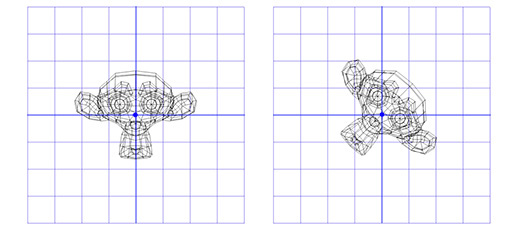
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:

Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.

Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).

Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.

Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.

Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.

Кватернионы

Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.

Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.

Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.

Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.

Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.

«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.

Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-prjamoj-koordinaty-normalnogo-vek/

http://habr.com/ru/post/131931/

[/spoiler]

Скалярное
произведение вектора самого на себя
называется скалярным квадратом. Эта
величина

определяет
квадрат длины вектора x.
Для обозначения длины (называемой
также нормой вектора)
используется обозначение

Например,

Рис.
16 Норма вектора

Вектор
единичной длины (||x||
= 1) называется нормированным. Ненулевой
вектор (x ≠ 0)
можно нормировать, разделив его на
длину, т.е. x =
||x||
(x/||x||)
= ||x|| e.
Здесь e =x/||x||
— нормированный вектор.

Векторы называются
ортонормированными, если все они
нормированы и попарно ортогональны.

Содержание

1.10. Угол между векторами

Скалярное
произведение определяет и угол φ
между двумя векторами x и y

Если вектора
ортогональны, то cosφ = 0 и φ = π/2, а если
они колинеарны, то cosφ = 1 и φ = 0.

Содержание 

1.11. Векторное представление матрицы

Каждую
матрицу A размера I×J можно
представить как набор векторов

Здесь
каждый вектор a_j является j-ым
столбцом, а вектор-строка b_i является i-ой
строкой матрицы A

Содержание 

1.12. Линейно зависимые векторы

Векторы
одинаковой размерности (N)
можно складывать и умножать на число,
также как матрицы. В результате получится
вектор той же размерности. Пусть имеется
несколько векторов одной
размерности x₁, x₂,…,x_K и
столько же чисел α α₁,
α₂,…,α_K.
Вектор 

y =
α₁x₁+
α₂x₂+…+
α_Kx_K  

называется линейной
комбинацией векторов x_k.

Если
существуют такие ненулевые числа α_k ≠
0, k =
1,…, K,
что y = 0,
то такой набор векторов x_k называется линейно
зависимым.
В противном случае векторы называются
линейно независимыми. Например,
векторы x₁ =
(2, 2)^t и x₂ =
(−1, −1)^t линейно
зависимы, т.к. x₁ +2x₂ = 0

Содержание 

1.13. Ранг матрицы

Рассмотрим
набор из K векторов x₁, x₂,…,x_K размерности N.
Рангом этой системы векторов называется
максимальное число линейно-независимых
векторов. Например в наборе

имеются
только два линейно независимых вектора,
например x₁ и x₂,
поэтому ее ранг равен 2. 

Очевидно,
что если векторов в наборе больше, чем
их размерность (K>N),
то они обязательно линейно зависимы. 

Рангом
матрицы (обозначается
rank(A))
называется ранг системы векторов, из
которых она состоит. Хотя любую матрицу
можно представить двумя способами
(векторы столбцы или строки), это не
влияет на величину ранга, т.к. 

rank(A)
= rank(A^t).

Содержание

1.14. Обратная матрица

Квадратная
матрица A называется
невырожденной, если она имеет
единственную обратную матрицу A^-1,
определяемую условиями

  AA⁻¹ = A⁻¹A = I.

Обратная матрица
существует не для всех матриц. Необходимым
и достаточным условием невырожденности
является 

det(A)
≠ 0 или rank(A)
= N.

Обращение матрицы
— это сложная процедура, для выполнения
которой существуют специальные программы.
Например,

Рис.
17 Обращение матрицы

Приведем формулы
для простейшего случая — матрицы 2×2

Если
матрицы A и B невырождены,
то 

(AB)⁻¹ = B⁻¹A⁻¹.

Содержание

1.15. Псевдообратная матрица

Если
матрица A вырождена
и обратная матрица не существует, то в
некоторых случаях можно
использовать псевдообратную матрицу,
которая определяется как такая матрица A⁺,
что

AA⁺A = A.

Псевдобратная
матрица — не единственная и ее вид
зависит от способа построения. Например
для прямоугольной матрицы можно
использовать метод
Мура-Пенроуза.

Если число столбцов
меньше числа строк, то 

A⁺=(A^tA)⁻¹A^t

Например, 

 

Рис.
17a Псевдообращение
матрицы

Если же число
столбцов больше числа строк, то

A⁺=A^t(AA^t)⁻¹

Содержание

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #