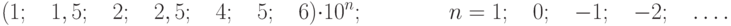Как найти нормируемая погрешность

Как найти нормируемая погрешность

Аннотация: Рассмотрим подробный порядок операций, выполняемых при обработке результатов измерений. Содержание всех описываемых действий рассмотрено в предыдущих разделах. Проводимые расчеты основываются на предположении о нормальном распределении погрешностей, когда систематические погрешности уже учтены на предыдущих этапах работы с экспериментальными данными.

Нормирование погрешностей средств измерений

Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.

Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.

Обычно нормирующее значение принимают равным:

  1. большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
  2. сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
  3. длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
  4. номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
  5. модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.

Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.

Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.

Указанное нормирование является гарантией взаимозаменяемости средств измерений.

Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.

Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.

Подход к нормированию погрешностей средств измерений заключается в следующем:

  1. в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
  2. порознь нормируют все свойства средств измерений, влияющие на их точность.

Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.

Классы точности средств измерений

Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.

Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.

Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.

Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.

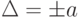
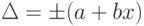
Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: $Delta=pm a$ или $Delta=pm (a+bx)$, где x – значение измеряемой величины или число делений, отсчитанное по шкале;
a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.

В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, “Класс точности М”, а на приборе – буквой “М”. Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле $gamma=Delta/x_{N}=pm p$, где xN – нормирующее значение, выраженное в тех же единицах, что и $Delta$; p – отвлеченное положительное число, выбираемое из ряда значений:

(1;quad 1,5;quad 2;quad 2,5;quad 4;quad 5;quad 6)cdot10^{n};qquadqquad n =1;quad 0;quad -1;quad - 2;quadldots.

Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.

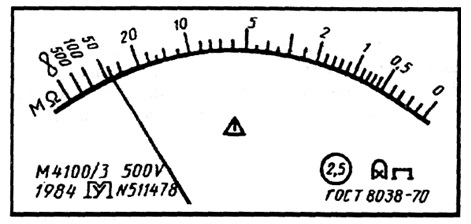
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка 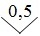, где 0,5 – значение числа р (рис. 3.1).

Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой

Рис.
3.1.
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой

В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).

Лицевая панель амперметра класса точности 1,5 с равномерной шкалой

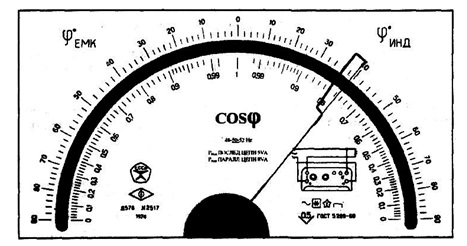
Рис.
3.2.
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой

В том случае если абсолютная погрешность задается формулой 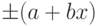$pm (a+bx)$, пределы допускаемой относительной основной погрешности

delta=Delta/x=pm[c+d(|x_{k}/x|-1)] (
3.1)

где с, d – отвлеченные положительные числа, выбираемые из ряда: 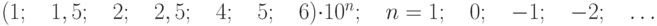$(1;quad 1,5;quad 2;quad 2,5;quad 4;quad 5;quad 6)cdot10^{n};quad n=1;quad 0;quad -1;quad - 2;quadldots$; – больший (по модулю) из пределов измерений. При использовании формулы 3.1 класс точности обозначается в виде “0,02/0,01”, где числитель – конкретное значение числа с, знаменатель – числа d (рис. 3.3).

Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой

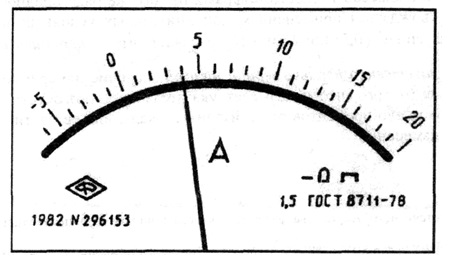
Рис.
3.3.
Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой

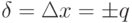
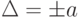
Пределы допускаемой относительной основной погрешности определяются по формуле $delta=Delta x=pm q$, если $Delta=pm a$. Значение постоянного числа q устанавливается так же, как и значение числа p. Класс точности на прибор обозначается в виде , где 0,5 – конкретное значение q (рис. 3.4).

Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой

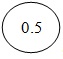
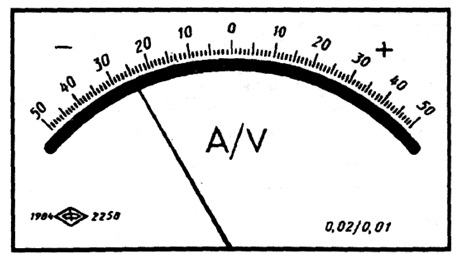
Рис.
3.4.
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой

В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.

Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.

Контрольные вопросы

  1. Поясните, что такое класс точности СИ.
  2. Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
  3. Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
  4. Как нормируются приборы по классам точности?
  5. Какие метрологические характеристики описывают погрешность средств измерений?
  6. Как осуществляется нормирование метрологических характеристик средств измерений?
Источник

Нормирование погрешностей средств измерения

Точность
средств измерения определяется предельно
допустимыми погрешностями, которые
могут иметь место при его использовании.

Нормированием
погрешностей средств измерений
называют
процедуру назначения допустимых границ
основной и дополнительных погрешностей,
а также выбор формы указания этих границ
в нормативно-технической документации.

Пределы
допускаемой основной и дополнительных
погрешностей определяются разработчиками
для каждого типа средств измерений на
стадии его проектирования и подготовки
производства. В зависимости от назначения
средства измерений и характера изменения
погрешности в пределах диапазона
измерений для средств измерений
различного типа нормируется предельно
допустимое значение: либо основной
абсолютной погрешности, либо основной
приведенной погрешности, либо основной
относительной погрешности.

Для
каждого типа средств измерений характер
изменения погрешности в пределах
диапазона измерений зависит от принципа
действия этого средства измерений и
может быть самым разнообразным. Однако,
как показала практика, среди этого
многообразия часто удается выделить
три типовых случая, предопределяющих
выбор формы представления пределов
допускаемой погрешности.

Типовые
варианты отклонения реальных передаточных
характеристик средств измерений от
номинальной характеристики (т.е.
зависимости показаний средства измерения
x
от действительного значения xд,
поданного на его вход) и соответствующие
им графики изменения предельных значений
абсолютной и относительной погрешностей
в зависимости от измеряемой величины
приведены на рис. 1.

Если
реальная передаточная характеристика
средства измерений смещена по отношению
к номинальной (1-й график на рис. 1, а),
то предельное значение абсолютной
погрешности средства измерения
(1-й
график на рис. 1, б)
не зависит от измеряемой величины.

Предельное
значение основной абсолютной погрешности
средства измерений, не изменяющееся от
значения измеряемой величины, называют
аддитивной
погрешностью.

Если
угол наклона реальной передаточной
характеристики средства измерений
отличается от номинального (2-й график
на рис. 1, а),
то предельное значение абсолютной
погрешности будет линейно зависеть от
измеряемой величины (2-й график на рис.
1, б).

Предельное
значение основной абсолютной погрешности
средства измерений, линейно изменяющееся
от значения измеряемой величины, называют
мультипликативной
погрешностью.

Если
реальная передаточная характеристика
средства измерений смещена по отношению
к номинальной и угол ее наклона отличается
от номинального (3-й график на рис. 1, а),
то в этом случае имеет место как
аддитивная, так и мультипликативная
составляющая предельного значения
основной абсолютной погрешности.

Аддитивная
погрешность определяется, например,
неточной установкой нулевого значения
перед началом измерений, уходом нуля в
процессе измерений, наличием термоэдс
в контактных соединениях и т.д.

а

б

в

Рис.
1. Иллюстрации
к выбору формы представления пределов
допус-
каемой
основной погрешности:

а
– типовые варианты отклонения реальных
передаточных характеристик средств
измерений от номинальной характеристики;
б
– пределы допускаемой абсолют-

ной погрешности; в
–
пределы допускаемой относительной
погрешности

Мультипликативная
погрешность определяется, например,
изменением коэффициентов усиления или
ослабления входных сигналов (например,
при изменении температуры окружающей
среды или вследствие старения элементов),
изменением значений, воспроизводимых
мерами, встроенными в измерительные
приборы, изменением жесткости пружин,
создающих противодействующий момент
в электромеханических приборах, и т.д.

Ширина
полосы неопределенности значений
абсолютной (рис. 1, б)
и относительной (рис. 1, в)
погрешностей характеризует разброс и
изменение в процессе эксплуатации
индивидуальных характеристик средств
измерений определенного типа.

А.
Нормирование пределов допускаемой
основной погрешности для средств
измерений с преобладающей аддитивной
погрешностью.

Для
средств измерений с преобладающей
аддитивной погрешностью (1-е графики на
рис. 1) одним числом (∆max=
±а)
удобно нормировать предельно допустимое
значение основной абсолютной погрешности.
В этом случае фактическая абсолютная
погрешность измерения ∆ может иметь
различные значения в различных точках
шкалы, но не должна превышать предельно
допустимой величины (∆ ≤ ±а).
В многопредельных измерительных приборах
с преобладающей аддитивной погрешностью
для каждого предела измерений пришлось
бы указывать свое значение предельно
допустимой абсолютной погрешности. К
сожалению, как видно из 1-го графика на
рис. 1, в,
нормировать одним числом предел
допускаемой относительной погрешности
в различных точках шкалы не представляется
возможным. По этой причине для средств
измерений с преобладающей аддитивной
погрешностью часто нормируют одним
числом значение так называемой основной
приведенной
относительной
погрешности:

,

где
xN
– нормирующее значение.

Таким
способом, например, нормируются
погрешности большинства электромеханических
и электронных приборов со стрелочными
индикаторами. В качестве нормирующего
значения xN
обычно используется предел измерений
(xN
= xmax),
удвоенное значение предела измерений
(если нулевая отметка находится в
середине шкалы) или длина шкалы (для
приборов с неравномерной шкалой). Если
xN
= xmax,
то значение приведенной погрешности γ
равно пределу допускаемой относительной
погрешности средства измерений в точке,
соответствующей пределу измерений. По
заданному значению предела допускаемой
основной приведенной погрешности легко
определить предел допускаемой основной
абсолютной погрешности для каждого
предела измерений многопредельного
прибора:

.

После
этого для любой отметки шкалы x
может быть произведена оценка предельно
допустимой основной относительной
погрешности:

.

Б.
Нормирование пределов допускаемой
основной погрешности для средств
измерений с преобладающей мультипликативной
погрешностью.

Как
видно из рис. 1 (2-й график), для средств
измерений с преобладающей мультипликативной
погрешностью одним числом удобно
нормировать предел допускаемой основной
относительной погрешности (рис. 1, в)
δmax
= ± b.
В этом случае фактическая относительная
погрешность измерений на различных
участках шкалы может иметь различные
значения, но не должна превышать предельно
допустимой величины (δ ≤ ± b).
По заданному значению предельно
допустимой относительной погрешности
δmax
для любой точки шкалы может быть
произведена оценка предельно допустимой
абсолютной погрешности:

.

К
числу средств измерений с преобладающей
мультипликативной погрешностью относится
большинство многозначных мер, счетчики
электрической энергии, счетчики воды,
расходомеры и др. Следует отметить, что
для реальных средств измерений с
преобладающей мультипликативной
погрешностью не удается полностью
устранить аддитивную погрешность. По
этой причине в технической документации
всегда указывается наименьшее значение
измеряемой величины, для которого предел
допускаемой основной относительной
погрешности еще не превышает заданного
значения δmax.
Ниже этого наименьшего значения
измеряемой величины погрешность
измерений не нормируется и считается
неопределенной.

В.
Нормирование пределов допускаемой
основной погрешности для средств
измерений с соизмеримыми аддитивной и
мультипликативной погрешностями.

Если
аддитивная и мультипликативная
составляющие погрешности средства
измерений соизмеримы (3-й график на рис.
1), то задание предельно допустимой
погрешности одним числом не представляется
возможным, поскольку предельные значения
абсолютных погрешностей будут определяться
выражением

.

В
этом случае нормируется либо предел
допускаемой абсолютной основной
погрешности (указываются предельно
допустимые значения a
и b),
либо (чаще всего) предел допускаемой
относительной основной погрешности. В
последнем случае выражение для оценки
численных значений предельно допустимых
относительных погрешностей в различных
точках шкалы приобретает следующий
вид:

,

где
xmax
– предел измерений; x
– измеренное значение; с
– предел допускаемой относительной
погрешности в конце диапазона измерения
данного прибора; d
– аддитивная относительная погрешность
прибора.

Рассмотренным
выше способом (указанием численных
значений с
и d)
нормируются, в частности, предельно
допустимые значения относительной
основной погрешности цифровых
измерительных приборов. В этом случае
предел основной относительной погрешности
каждого экземпляра средств измерений
определенного типа не должен превышать
установленных для этого типа средств
измерений значений предельно допустимой
погрешности:

.

При этом значение
абсолютной основной погрешности не
должно превышать величины

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Основные погрешности средств измерения нормируются путем задания пределов допускаемой основной погрешности, при которой средство измерения (СИ) по техническим требованиям может быть допущено к применению.

Для того чтобы оценить погрешность, которую внесет данное СИ в конечный результат, пользуются предельными значениями погрешности для данного типа СИ.

Предел допускаемой основной абсолютной погрешности D может быть представлен одним из трех способов:

– постоянным для любых значений X числом, характеризующим аддитивную погрешность,

D = ± а;                                                                      (6.1)

– в виде двухчленной формулы, включающей аддитивную и мультипликативную погрешности,

D = ± (а + bх);                                                            (6.2)

– в виде уравнения

D=f(х)                                                                     (6.3)

При сложной зависимости (6.3) допускается представлять погрешность в виде графика и таблицы.

Пределы допускаемой относительной погрешности для случая (6.1) в процентах выражают формулой

                                                        (6.4)

для случая  (6.2) – формулой

 

где Хк – предел измерений;

 – имеет смысл приведенной погрешности в  конце диапазона измерений (при Х=Хк);

     – имеет смысл приведенной погрешности в начале  диапазона измерений (при Х = 0), причем c > d.

Предел допускаемой приведенной погрешности в процентах выражается формулой

                                                         (6.5)

где р – отвлеченное положительное число.

Согласно ГОСТ 8.401-80 для указания нормированных пределов допускаемых погрешностей значения р, q, с, d выражаются в процентах и выбираются из ряда чисел: (1;1,5;2;2,5;3;4;5 и 6)  ´10n , где n=+1;0;-1;-2;-3 и т.д.

В настоящее время в эксплуатации большое число средств измерений, метрологические характеристики которых нормируются на основе классов точности.

Класс точности – обобщенная характеристика средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значение которых устанавливают в соответствующих стандартах.

Класс точности позволяет судить о том, в каких пределах находится погрешность средст измерений одного типа, но не характеризует точности измерений, выполняемых такими средствами, так как погрешность зависит и от метода измерений, и от условий измерений и т.д.

С использованием чисел указанного выше ряда чисел разработаны следующие условные обозначения классов точности СИ, наносимые на них.

1. Класс точности указывают просто одним из чисел приведенного выше предпочтительного ряда р (например, 1,5). Это используют для СИ, у которых предел допускаемой приведенной погрешности постоянен (присутствует только аддитивная погрешность), как в (6.1), Xn в (6.5) выражена в единицах измеряемой величины. Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой или степенной (с показателем  степени не более двух) шкалой.

2.   Класс точности указывает числом из приведенного выше ряда, под которым ставится треугольная скобка, например,        . Такое обозначение применяют для приборов с резко неравномерной шкалой, для которых  Хn выражают в единицах длины шкалы (мм, см, условных делениях). В этом случае при измерении, кроме значения измеряемой величины, обязательно должен быть записан отсчет X в единицах длины шкалы и предел Хn в этих же единицах, иначе нельзя будет вычислить погрешность результата. Таким способом обозначают класс точности омметров.

3. Число, обозначающее класс точности, обводят кружком например,       . Такое обозначение применяют для СИ, у которых предел допускаемой относительной погрешности постоянен во всем диапазоне измерений (имеется только мультипликативная погрешность, (a в (6.2) равна нулю) и его определяют по (6.4). Таким способом нормируют погрешности измерительных мостов, магазинов, масштабных преобразователей. При этом обычно указывают границы рабочего диапазона, для которых справедлив данный класс точности.

4. Класс точности обозначается двумя числами, записываемыми через косую черту, т. е. в виде условной дроби c/d, например, 0,02 / 0,01. Такое обозначение применяют для СИ, у которых погрешность нормирована по двухчленной формуле (6.2). Таким способом указывают классы точности цифровых вольтметров, высокоточных потенциометров постоянного тока и других высокоточных приборов.

Источник

Добавить комментарий