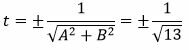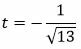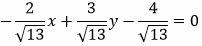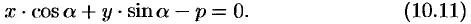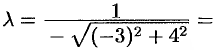Простейшей
из линий является прямая. Разным способам
задания прямой соответствуют в
прямоугольной системе координат разные
виды ее уравнений.
Уравнение
прямой с угловым коэффициентом.
Пусть
на плоскости
задана произвольная прямая, не
параллельная оси
.
Ее положение вполне определяется
ординатой
точки
пересечения с осью
и углом
между осью
и прямой (см. рис. 10.10).
Под
углом
(
)
наклона
прямой понимается наименьший угол, на
который нужно повернуть вокруг точки
пересечения прямой и оси
против часовой стрелки ось
до ее совпадения с прямой.
Возьмем
на прямой произвольную точку
(см. рис. 10.10). Проведем через точку
ось
,
параллельную оси
и одинаково с ней направленную. Угол
между осью
и прямой равен
.
В системе
точка
имеет координаты
и
.
Из определения
тангенса угла следует равенство
,
т. е.
.
Введем
обозначение
,
получаем
уравнение
,
(10.1)
которому
удовлетворяют координаты любой точки
прямой. Можно убедиться, что координаты
любой точки
,
лежащей вне данной прямой, уравнению
(10.1) не удовлетворяют.
Определение.
Число
называется угловым
коэффициентом прямой,
а уравнение (10.2) — уравнением
прямой с угловым коэффициентом.
Если
прямая проходит через начало координат,
то
и, следовательно, уравнение этой
прямой будет иметь вид
.
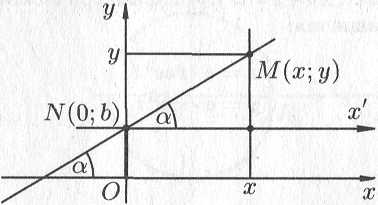
Рис. 10.10
Если
прямая параллельна оси
,
то
,
следовательно,
и уравнение (10.1) примет вид
(10.2)
Если
прямая параллельна оси
,
то
,
уравнение (10.1) теряет смысл, т. к. для
нее угловой коэффициент
не существует. В этом случае уравнение
прямой будет иметь вид
,
(10.3)
где
— абсцисса точки пересечения прямой с
осью
.
Отметим, что уравнения (10.2) и (10.3) есть
уравнения первой степени.
Общее
уравнение прямой.
Рассмотрим
уравнение первой степени относительно
и
в общем виде
,
(10.4)
где
,
,
— произвольные
числа, причем
и
не
равны нулю одновременно.
Покажем, что
уравнение (10.4) есть уравнение прямой
линии. Возможны два случая.
Если
,
то уравнение (10.4) имеет вид
,
причем
,
т.е.
— Это есть уравнение прямой, параллельной
оси
и проходящей через точку
.
Если
,
то из уравнения (10.4) получаем
.
Это есть уравнение прямой с угловым
коэффициентом
.
Итак,
уравнение (10.4) есть уравнение прямой
линии, оно называется общим уравнением
прямой.
Некоторые частные
случаи общего уравнения прямой:
-
если
,
то уравнение приводится к виду
.
Это есть уравнение прямой, параллельной
оси;
-
если
,
то прямая параллельна оси;
-
если
,
то получаем
.
Уравнению удовлетворяют координаты
точки
,
прямая проходит через начало координат.
Уравнение
прямой, проходящей через данную точку
в данном направлении.
Пусть
прямая проходит через точку
и ее направление характеризуется угловым
коэффициентом
.
Уравнение этой прямой можно записать
в виде
,
где
— пока неизвестная величина. Так как
прямая проходит через точку
,
то координаты точки удовлетворяют
уравнению прямой:
.
Отсюда
.
Подставляя
значение
в уравнение
,
получим искомое уравнение прямой
,
т. е.
(10.5)
Определение.
Уравнение
(10.5) с различными значениями
называют также уравнениями пучка прямых
с центром в точке
.
Из
этого пучка нельзя определить лишь
прямую, параллельную оси
.
Уравнение
прямой, проходящей через две точки.
Пусть
прямая проходит через точки
и
.
Уравнение
прямой, проходящей через точку
,
имеет вид
,
(10.6)
где
— пока неизвестный коэффициент.
Так
как прямая проходит через точку
,
то координаты этой точки должны
удовлетворять уравнению (10.6):
.
Отсюда находим
.
Подставляя найденное значение
в уравнение (10.6), получим уравнение
прямой, проходящей через точки
и
:
(10.7)
Предполагается,
что в этом уравнении
,
.
Если
,
то прямая, проходящая через точки
и
параллельна оси ординат. Ее уравнение
имеет вид
.
Если
,
то уравнение прямой может быть записано
в виде
,
прямая
параллельна оси абсцисс.
Уравнение
прямой в отрезках.
Пусть
прямая пересекает ось
в точке
,
а ось
— в точке
(см. рис. 10.11). В этом случае уравнение
(10.7) примет вид
,
т.е.
Это
уравнение называется уравнением
прямой в отрезках,
так как числа
и
указывают, какие отрезки отсекает
прямая на осях координат.
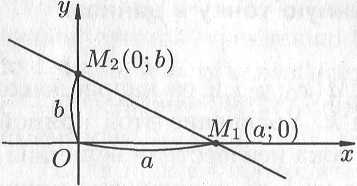
Рис. 10.11
Уравнение
прямой, проходящей через данную точку
перпендикулярно данному вектору.
Найдем
уравнение прямой, проходящей через
заданную точку
перпендикулярно данному ненулевому
вектору
.
Возьмем
на прямой произвольную точку
и рассмотрим вектор
(см. рис. 10.12). Поскольку векторы
и
перпендикулярны, то их скалярное
произведение равно нулю:
,
то есть
(10.8)

Рис. 10.12
Определение.
Уравнение
(10.8) называется уравнением прямой,
проходящей через заданную точку
перпендикулярно заданному вектору.
Вектор
,
перпендикулярный
прямой, называется нормальным
вектором
этой прямой.
Уравнение (10.8)
можно переписать в виде
(10.9)
где
и
— координаты
нормального вектора,
— свободный член. Уравнение (10.9) есть
общее уравнение прямой (см. (10.4)).
Полярное
уравнение прямой.
Найдем
уравнение прямой в полярных координатах.
Ее положение можно определить, указав
расстояние
от полюса
до данной прямой и угол
между полярной осью
и осью
,
проходящей через полюс
перпендикулярно данной прямой (см. рис.
10.13).
Для
любой точки
на данной прямой имеем:
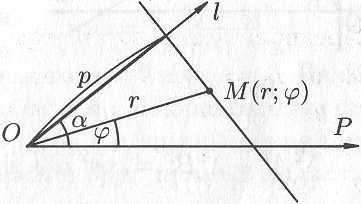
Рис. 10.13
С другой стороны,
.
Следовательно,
(10.10)
Полученное
уравнение (10.10) и есть уравнение прямой
в полярных координатах.
Нормальное
уравнение прямой.
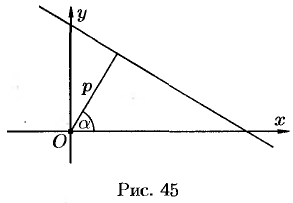
Пусть
прямая определяется заданием
и
(см. рис. 10.14). Рассмотрим прямоугольную
систему координат
.
Введем полярную систему, взяв
за полюс и
за полярную ось. Уравнение прямой можно
записать в виде
,
т. е.
.
Но,
в силу формул, связывающих прямоугольные
и полярные координаты, имеем:
,
.
Следовательно, уравнение (10.10) прямой в
прямоугольной системе координат примет
вид
(10.11)
Уравнение
(10.11) называется нормальным
уравнением прямой.
Покажем, как
привести уравнение (10.4) прямой к виду
(10.11).
Умножим
все члены уравнения (10.4) на некоторый
множитель
.
Получим
.
Это уравнение должно обратиться в
уравнение (10.11). Следовательно, должны
выполняться равенства:
,
,
.
Из первых двух равенств находим
, т.е.
.
Множитель
называется нормирующим множителем.
Согласно
третьему равенству
знак нормирующего множителя противоположен
знаку свободного члена
общего уравнения прямой.
Рис. 10.14
Пример
10.2.
Привести
уравнение
к нормальному виду.
Решение.
Находим нормирующий множитель
.
Умножая
данное уравнение на
,
получим искомое нормальное
уравнение
прямой:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормиро́вочный мно́житель — фактор, на который домножается математическое выражение, чтобы после этого какой-либо значимый параметр оказался равным 1. Подбор нормировочного множителя называется нормированием (нормировкой).
Чаще всего имеется в виду ситуация, когда на нормировочный фактор домножаются неотрицательная функция или все члены числового ряда, чтобы интеграл от функции по области определения или сумма членов ряда равнялись единице. Тогда фактор представляет собой положительное число или алгебраическое выражение, не зависящее от аргументов функции. Подобная нормировочная процедура применяется в теории вероятностей и в различных областях физики (статфизике, квантовой механике, теории спектров и других). После нормировки функция может рассматриваться как плотность распределения, а ряд как ряд распределения.
Однако понятия «нормировочный множитель», «нормировка» используются и в иных, не связанных со статистикой ситуациях. Целью нормировки при этом может быть приведение данных к в чём-то более удобному виду.
Нормировочный множитель в статистике[править | править код]
Задачи, прямо или косвенно относящиеся к статистике, составляют основную сферу применения нормировочных множителей. Общий смысл состоит в наложении требования равенства суммарной вероятности всех возможных событий единице[1].
Процедура нормировки[править | править код]
Если 


,
при этом функция 
Если 


,
при этом последовательность 

Потребность в нормировке[править | править код]
Наиболее значимые и часто встречающиеся распределения, как правило, записываются уже с нормировкой, то есть никаких дополнительных процедур не требуется. Например, нормальное распределение величины 

,
Здесь предполагается область определения 

Однако в менее распространённых ситуациях подбор нормировочного множителя может потребоваться. Скажем, иногда нужно сузить область определения 




Примеры из области физики[править | править код]
Пример 1. Распределение Максвелла для модулей скоростей молекул идеального газа имеет вид 






Пример 2. Состояние частицы в квантовой механике задаётся волновой функцией 




Пример 3. Непрерывный электромагнитный или акустический спектр может быть задан в виде некоей функции 









Нормировочные факторы вне статистики[править | править код]
Нормировочные множители также используются, когда желательно добиться того, чтобы какая-то величина (не обязательно имеющая смысл полной вероятности) оказалась равной единице.
- Нормировка
(и, соответственно, подбор нормировочного множителя) могут потребоваться не только для вышеупомянутого физического случая волновой функции, но и для собственных функций в более широком классе задач[3].
Примечания[править | править код]
- ↑ А. И. Волковец, А. Б. Гуринович Теория вероятностей и математическая статистика. Минск, БГУИР (2003), см. ф-лы: (4.9), (8.7), (10.8).
- ↑ П. С. Парфенов Квантовая механика. Методическое пособие к практикуму по квантовой физике. СПб: ИТМО (2012), см. 1.1.4. Нормирование волновых функций.
- ↑ Н. Н. Воробьев Теория рядов. М.: Наука (1979), см. гл. 8, § 3: Нормированные и ортогональные функции.
- ↑ И. Мальцевская Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач, см. на образовательном сервисе Zaochnik.
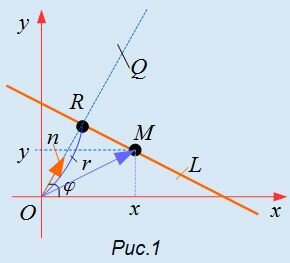
Пусть l – произвольная прямая (рис. 102).
Обозначим через p расстояние от начала координат до прямой l, а через φ – угол между осью Ох и нормальным вектором прямой l. Угол будем отсчитывать от оси Оx в направлении, противоположном движению часовой стрелки. Очевидно, что положение прямой на плоскости полностью определяется заданием величин p и φ. Выразим коэффициенты уравнения прямой l через p и φ.
Пусть M0 – точка пересечения прямой l и перпендикулярной ей прямой, проходящей через начало координат, n0 – единичный нормальный вектор прямой l, т. е. |n0| = 1. Координаты точки M0 и вектора n0 выражаются через заданные величины p и φ следующим образом:
Известно уравнение прямой, проходящей через точку (х0; у0) с нормальным вектором <А; В):
х cos φ + у sin φ – р (cos 2 φ + sin 2 φ) = 0.
х cos φ + у sin φ – р = 0.
Оно называется нормированным уравнением прямой.
В нормированном уравнении все коэффициенты имеют геометрический смысл: коэффициенты при переменных х и у – координаты единичного нормального вектора прямой; свободный член (-р) равен расстоянию от начала координат до прямой, взятому со знаком «минус». Подчеркнем еще раз, что в нормированном уравнении прямой свободный член меньше или равен нулю.
Рассмотрим, например, уравнение х – у + 5√ 2 = 0. Оно не является нормированным: вектор (1; -1) не единичный, так как | n | =√ 2 =/=1; свободный член уравнения положителен. Умножим обе части уравнения на (- 1 /√ 2 ). Тогда уравнение прямой примет вид
и станет нормированным, так как теперь вектор (- 1 /√ 2 ; 1 /√ 2 ) очевидно, единичный, а свободный член уравнения отрицателен. Нормальный вектор рассматриваемой прямой образует с осью Оx угол φ такой, что cos φ = – 1 /√ 2 , sin φ = 1 /√ 2 ,
т. е. φ = 135°. Прямая проходит на расстоянии 5 единиц длины от начала координат.
всегда можно привести к нормированному виду (нормировать). Если С 0 сводится к предыдущему умножением обеих частей уравнения на -1. Поэтому, если С > 0, то за нормирующий множитель следует взять число ( -frac<1><sqrt> )
Задача. Вычислить расстояние от начала координат до прямой 6x – 8y + 25 = 0.
Тaк как С = 25 > 0, то, умножив обе части уравнения на нормирующий множитель
получим нормированное уравнение данной прямой
Учитывая геометрический смысл свободного члена нормированного уравнения прямой, видим, что искомое расстояние равно 2,5.
Нормальное уравнение прямой
В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 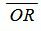
Выразим уравнение прямой L через два параметра: длину отрезка 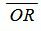
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора 
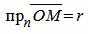 |
(3) |
Скалярное произведение векторов n и 
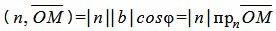 , , |
(4) |
где 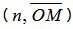


Поскольку n единичный вектор, то (4) можно записать так:
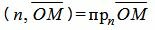 . . |
(5) |
Учитывая, что n=<cosφ, sinφ>, 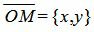
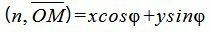 . . |
(6) |
Тогда из уравнений (3), (5), (6) следует:
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой .
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
Подставляя вычисленные значения в (7) получим:
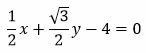
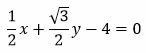
Приведение общего уравнения прямой на плоскости к нормальному виду
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи “Общее уравнение прямой на плоскости”), то существует такое число t, что
| tAx=cosφ, tB=sinφ, tC=−r. | (9) |
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 =cos 2 φ+sin 2 φ=1. | (10) |
Упростим выражение и найдем t:
t 2 A 2 +t 2 B 2 =t 2 (A 2 +B 2 )=1,
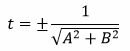 . . |
(11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение прямой
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
Так как C>0, то знак t отрицательный:
Умножим уравнение (12) на t:
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
Отметим, что число 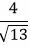
Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
Пусть дана некоторая прямая L. Проведём через начало координат прямую n, перпендикулярно данной и назовём её нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L. На нормали введём направление от точки O к точке N.
Обозначим через угол, на которой нужно повернуть против часовой стрелки ось Ox до совмещения её положительного направления с направлением нормали, через p длину отрезка ON.
. (1)
будет нормальным уравнением прямой.
С помощью нормального уравнения прямой можно определить расстояние от данной точки плоскости до прямой. Пусть – точка, не лежащая на прямой, заданной нормальным уравнением. Требуется определить расстояние d от точки до прямой. Это расстояние определяется по формуле
. (2)
Общее уравнение прямой можно привести к нормальному виду. Пусть
– общее уравнение прямой, а
– её нормальное уравнение.
Так как оба уравнения определяют одну и ту же прямую, их коэффициенты пропорциональны.
Очевидно, для получения нормального уравнения следует все члены общего уравнения умножить на постоянный множитель , вычисляемый по формуле
. (3)
В этой формуле берётся знак, противоположный знаку C в общем уравнении прямой.
Таким образом, получаем уравнение
, (4)
которое и будет нормальным уравнением прямой на плоскости.
Пример 1. Привести общее уравнение прямой к нормальному виду.
Решение. Вычисляем нормирующий множитель:
(знак, противоположный C).
Умножаем все члены общего уравнения на нормирующий множитель и получаем:
.
Пример 2. Привести общее уравнение прямой к нормальному виду.
Решение. Вычисляем нормирующий множитель:
(знак, противоположный C).
Умножаем все члены общего уравнения на нормирующий множитель и получаем:
.
Пример 3. Найти расстояние от точки до прямой .
Решение. Приведём данное уравнение к нормальному виду. Вычисляем нормирующий множитель:
(знак, противоположный C).
Умножаем все члены общего уравнения на нормирующий множитель и получаем нормальное уравнение:
.
По формуле (2) находим искомое расстояние:
.
[spoiler title=”источники:”]
http://matworld.ru/analytic-geometry/normalnoe-uravnenie-prjamoj.php
http://function-x.ru/line6.html
[/spoiler]
что такое нормировочный множитель….объясните пожалуйста,и как его находить? спасибо за ответы
Ученик
(104),
закрыт
9 лет назад
Саша Русанов
Высший разум
(209180)
9 лет назад
Норм. множитель встречаются в разных областях . Смысл в том , чтобы сумма каких либо объектов или объект нормировались на 1.
Например , есть вектор ( a,b,c) с длиной(нормой) L . А нам нужен вектор такого же напрвления , но единичной длины. N = ( a,b,c)/L =( a,b,c)/sqrt(a^2+b^2+c^2)/
M =1/ sqrt(a^2+b^2+c^2) и есть нормирующий множитель.
Вероятности тоже нормированы на 1. – Вероятность полной системы событий равна 1.
Нормальное уравнение прямой
Пусть прямая определяется заданием 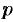
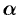
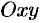
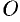
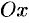
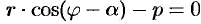
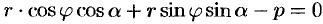
Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем: 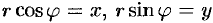
Уравнение (10.11) называется нормальным уравнением прямой.
Покажем, как привести уравнение (10.4) прямой к виду (10.11).
Умножим все члены уравнения (10.4) на некоторый множитель 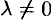
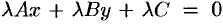
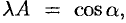
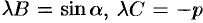
равенств находим
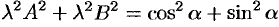
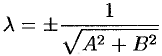
Множитель 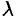
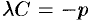
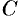
Пример №10.2.
Привести уравнение 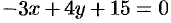
Решение:
Находим нормирующий множитель 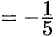
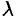
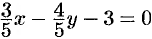
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
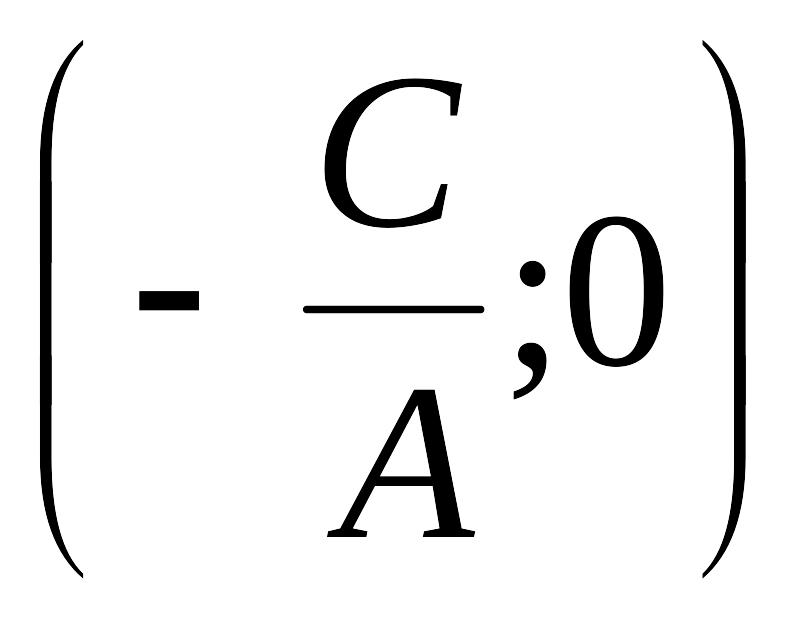
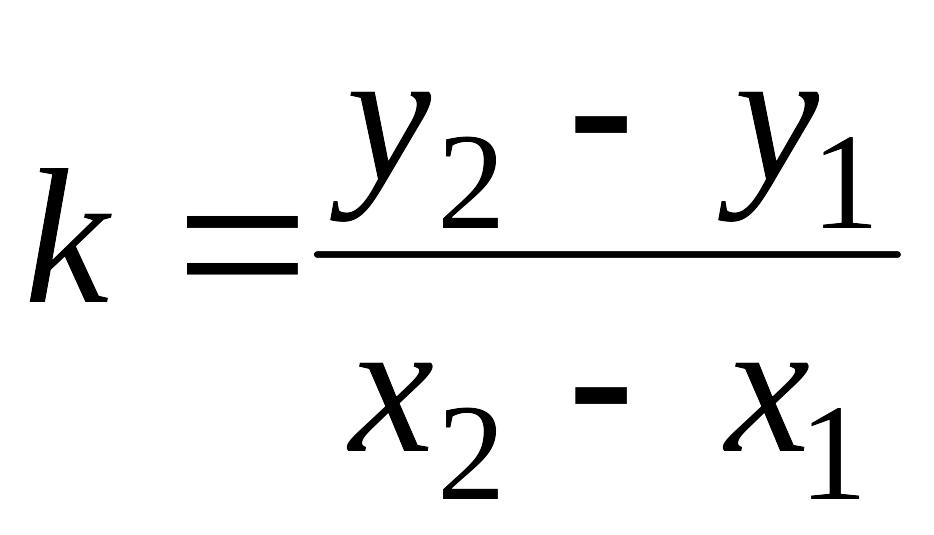
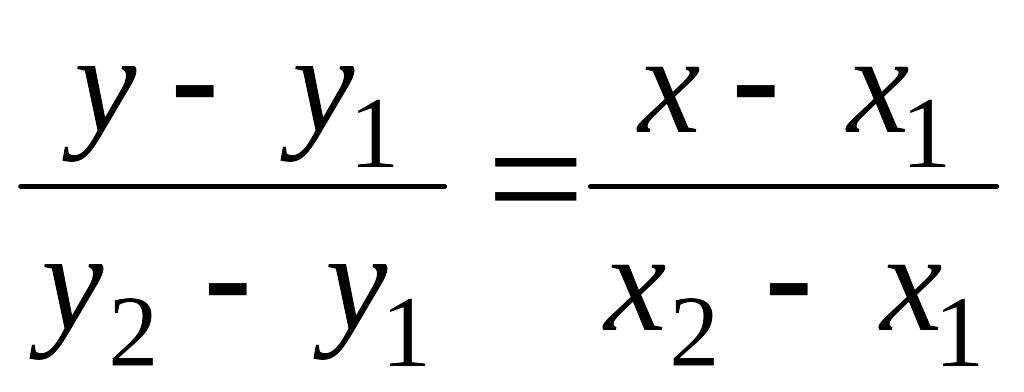
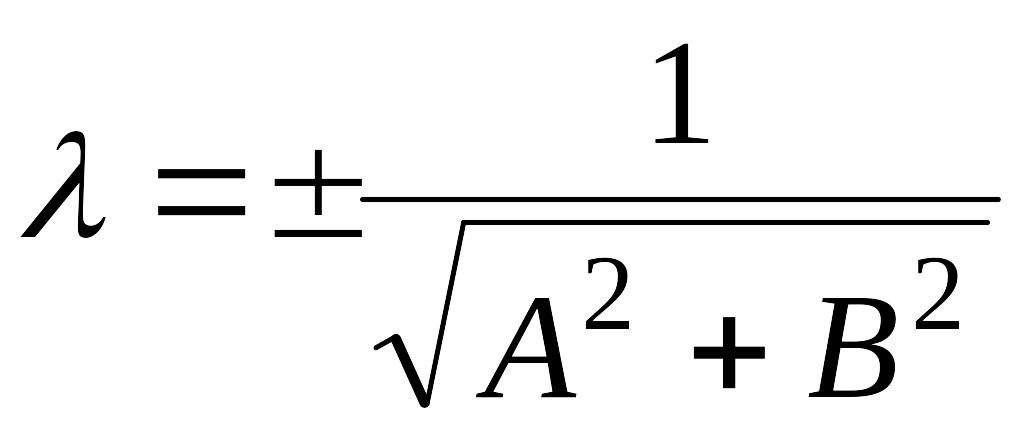
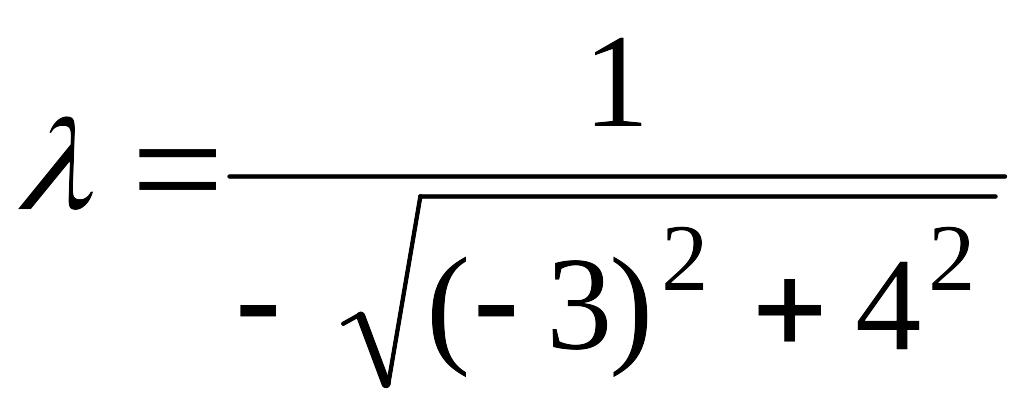
![{displaystyle A=left[int _{x_{1}}^{x_{2}}phi (x),dxright]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0fcca8f170a090edda6c2d612c11b340ce4f64d)
![{displaystyle A=left[sum limits _{n}p(x_{n})right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4fd74d778c97c0ea3fd48c4a7c67c5406b8047)