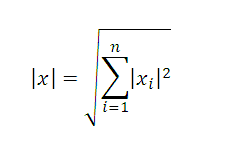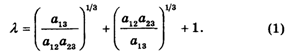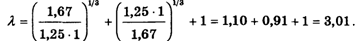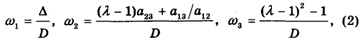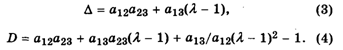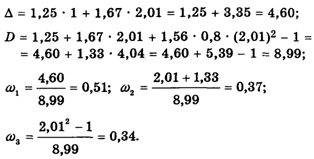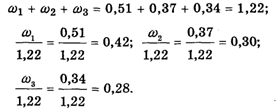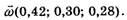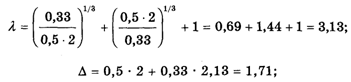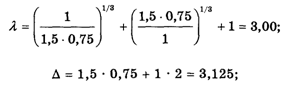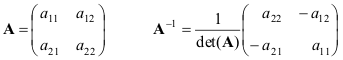Как найти нормирующий вектор

Была ли эта статья полезной?

9.3. Метод собственного вектора

Математические методы позволяют эффективно ана­лизировать весьма сложные и большие системы, модели которых состоят из нескольких уровней. Например, из­вестная модель мировой динамики Форрестера и Медоуза рассматривает ресурсы, население, уровень жизни, капиталовложения, загрязнение среды. Анализ состояния окружающей среды приводит к модели, уровнями которой могут быть: 1) типы загрязнителей SO2, NO4, CO2, CO, стоки вод, твердые отходы, земля), 2) способы очистки, 3) очистительные устройства. Изучение вопро­са об общем благосостоянии страны целесообразно про­водить по таким уровням: 1) экономика, оборона, здра­воохранение; 2) отрасли промышленности; 3) ресурсы; 4) демография. Уровни располагаются по их значимо­сти, т. е. образуют Иерархию. Анализ таких Иерархиче­ских систем, сводится прежде всего к тому, чтобы для каждого уровня выбрать Приоритеты и в соответствии с ними расположить объекты этого уровня. Основная цель анализа: выяснить, насколько влияют факторы самого низкого уровня на общую цель. Покажем на конкретном примере, как это делают Методом соб­ственного вектора. Этот метод позволяет расположить рассматриваемые объекты по степени их значимости путем попарного сравнения по различным независимым признакам.

На должность юриста крупного предприятия претендуют трое (обозначим их А, В, С). Директор предприя­тия в большом затруднении, т. к. среди претендентов нет такого, кто превосходил бы остальных по всем парамет­рам. Один имеет больший опыт, зато другой имеет луч­шее образование и опубликовал несколько научных работ; третий известен своей исключительной ответствен­ностью и добросовестностью и т. д. Как выбрать Наи­лучшего по совокупности качеств? Тут директор вспомнил, что в институте экологии и права, где он учился, им преподавали математику, и, в частности, рассказывали о применении математических методов в теории принятия решений. Покопавшись в своих архи­вах, директор нашел лекции по математике и решил воспользоваться методом собственных векторов, приме­няемом при изучении иерархических систем.

Во-первых, он выбрал 3 основных критерия, по которым будут сравниваться кандидаты: профессионализм и опыт (критерий К1), ответственность и добросовест­ность (К2), организаторские способности (K3). По такому важному критерию как честность и порядочность пре­тендентов сравнить было невозможно — у всех троих в характеристиках было написано по этому поводу прак­тически одно и то же. Первая задача состояла в том, чтобы расположить эти критерии в порядке важности. Вторая задача состояла в том, чтобы сравнить кандида­тов между собой по каждому из этих критериев, припи­сав каждому из них определенный балл.

Этап первый: сравнение критериев.

Исходя из своего жизненного и профессионального опыта, директор полагал, что критерий К1 важнее, чем критерии К2 и К3, причем, если сравнивать их количе­ственно, в баллах, то К1 : К2

5 : 3. При этом, если, сравнивать последние два качества между со­бой, то они примерно равноценны, т. е. можно считать, что K2 : K3

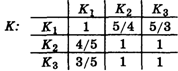
1 : 1. Далее директор составил матрицу К Размером 3´3, т. е. таблицу с тремя строками и тремя столбцами, куда занес отношения указанных баллов:

Число, стоящее на пересечении строки с номером I и столбца с номером J, обычно обозначают АIj. Поэтому у нас A11 = 1, A22 = 1, А33 = 1, A12 = 5/4, A13 = 5/3, А23 = 1, и т. д. Заметьте, что числа Aij и АJi являются взаимно обратными.

Все дальнейшие вычисления будем проводить вместе с директором приближенно, округляя до сотых долей, причем нам понадобятся только числа А12 = 1,25; A13 = 1,67 и A23 = 1.

Прежде всего находят так называемое Главное собственное число L матрицы К по формуле

Пользуясь калькулятором, получаем:

Теперь находим координаты W1, W2 и W3 так называемо­го Главного собственного вектора матрицы К по фор­мулам

Подставляя сюда наши значения А12 = 1,25; A13 = 1,67;

A23 = 1, последовательно получаем:

Теперь собственный вектор 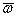(W1, W2, W3) Нужно Норми­ровать, т. е. каждую координату разделить на сумму всех координат. Имеем:

Сумма полученных чисел равна единице. Обозначим вектор, координатами которого являются эти числа, также буквой :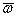

Этот вектор называется Вектором приоритетов. Соглас­но теории, качества К1, К2 и K3 можно расположить по приоритету с баллами 0,42; 0,30 и 0,28 соответственно.

Этап второй: сравнение претендентов по качеству К1. Из имеющихся у него документов (характеристик, рекомендаций, отзывов, научных публикаций) директор сумел сравнить между собой каждую пару претендентов по качеству К1. У него получилось А : В

1 : 2 (т. е. у В Балл в 2 раза выше, чем у А), А : С

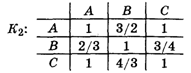
2 : 1. Поэтому матрица К1 попарных сравнений получилась такая

Из нее видно, что А12 = 0,5, А13 = 0,33, А23 = 2. Подстав­ляя эти числа в формулы (1)-(4), как и в предыдущем случае находим:

Итак, в этом случае вектор приоритетов будет 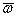(0,17; 0,48; 0,35), т. е., если сравнивать, претендентов по качеству К1, то они получают баллы 0,17, 0,48 и 0,35 соответственно.

Этап третий: сравнение претендентов по качеству K2:

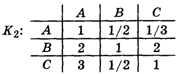
Как было видно из документов, каждые двое из пре­тендентов работали некоторое время в одной и той же фирме и вели примерно одинаковые дела. Просмотрев последние и оценив качество исполнения, директор по­лучил следующие отношения при попарном сравнении по критерию K2: А : В

3 : 4. Запишем матрицу К2 попарных сравнений:

Вектор приоритетов будет 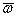(0,38; 0,26; 0,36), так что по качеству К2 претенденты получают баллы 0,38, 0,26 и 0,36 соответственно.

Этап четвертый: сравнение по качеству K3. Поскольку никто из претендентов прежде не нахо­дился на руководящей работе, то директор, исходя из весьма туманных соображений и своей интуиции, смог только оценить вероятность того, что тот или иной пре­тендент станет хорошим руководителем. Получились вероятности 0,8, 0,7 и 0,6 соответственно. Таким обра­зом, удалось обойтись без попарного сравнения. 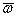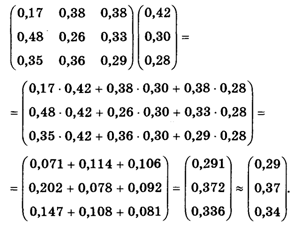Разде­лив каждое из указанных чисел на их сумму 0,8 + 0,7 + 0,6 = 2,1, находим вектор приоритетов: (0,38; 0,33; 0,29).

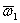
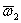
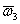
Этап пятый: получение окончательно результата. Согласно теории, окончательное распределение мест получается следующим образом. Составим из векторов , и матрицу 3´3, записав их координаты в столбцы:

Затем умножим эту матрицу на матрицу-столбец

Составленную из координат вектора 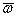. По правилу ум­ножения матриц,

Итак, окончательное распределение мест следующее:

Претендент А набрал 0,29 балла, претендент В — 0,37 балла, претендент C — 0,34 балла. Метод собственного вектора отдал предпочтение претенденту В.

Предупреждение: не попадайте под гипнотическое воздействие чисел! Несмотря на объективность матема­тических методов, полученный результат нельзя рас­сматривать как истину в последней инстанции. Хотя бы потому, что выбор исходного материала (т. е. чисел А12, а13 и А23, входящих в матрицы К1, К2, К3), был в зна­чительной степени субъективным. Поэтому и претен­дент С, имеющий примерно такой же балл, как и В, Также имеет шанс на успех, в особенности, если он не курит или согласен на меньшую зарплату.

1. Описанным методом можно сравнивать любое число кандидатов и по любому числу критериев, однако при большом их числе придется пользоваться другими формулами, приведенными, например, в книге Т. Саати «Принятие решений».

2. Вычислительные трудности, разумеется, можно переложить на ЭВМ.

3. Мы сознательно упростили ситуацию, опустив не­которые тонкости, связанные с оценкой метода. О них также можно прочитать в книге Т. Саати.

4. Еще раз отметим, в чем сила описанного метода. Сравнить каждые два объекта между собой по одному критерию довольно просто, и это дает возможность сравнительно легко заполнить матрицу попарных срав­нений. Но затем, с помощью несложных вычислений, мы находим ответ уже на довольно трудный вопрос: ка­кой из рассматриваемых объектов превосходит осталь­ные по совокупности всех критериев.

Метод собственного вектора можно применять для анализа самых разнообразных проблем, о которых шла речь в начале параграфа. Например, автор упомянутой выше книги проанализировал этим методом рост терро­ризма для агентства по контролю над вооружениями и разоружением в Вашингтоне.

В качестве самостоятельной задачи попробуйте оце­нить претендентов на должность мэра Вашего города, выбрав критерии по своему усмотрению.

Как найти нормированный собственный вектор

Найдем такие вектора (называются собственными векторами) v
и такие числа – значения (называются собственными значениями) l
матрицы A, для v, l и A выполняется:
A*v = l*v.

Также вычисляется кратность собственных значений и находит характеристическое уравнение матрицы.

© Контрольная работа РУ – калькуляторы онлайн

Где учитесь?

Для правильного составления решения, укажите:

Собственные векторы матрицы

Онлайн калькулятор нахождение собственных чисел и собственных векторов – Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.

[spoiler title=”источники:”]

http://www.kontrolnaya-rabota.ru/s/matrix/sobstvennyie/

http://allcalc.ru/node/648

[/spoiler]

Скалярное
произведение вектора самого на себя
называется скалярным квадратом. Эта
величина

определяет
квадрат длины вектора x.
Для обозначения длины (называемой
также нормой вектора)
используется обозначение

Например,

Рис.
16 Норма вектора

Вектор
единичной длины (||x||
= 1) называется нормированным. Ненулевой
вектор (x ≠ 0)
можно нормировать, разделив его на
длину, т.е. x =
||x||
(x/||x||)
= ||x|| e.
Здесь e =x/||x||
— нормированный вектор.

Векторы называются
ортонормированными, если все они
нормированы и попарно ортогональны.

Содержание

1.10. Угол между векторами

Скалярное
произведение определяет и угол φ
между двумя векторами x и y

Если вектора
ортогональны, то cosφ = 0 и φ = π/2, а если
они колинеарны, то cosφ = 1 и φ = 0.

Содержание 

1.11. Векторное представление матрицы

Каждую
матрицу A размера I×J можно
представить как набор векторов

Здесь
каждый вектор a_j является j-ым
столбцом, а вектор-строка b_i является i-ой
строкой матрицы A

Содержание 

1.12. Линейно зависимые векторы

Векторы
одинаковой размерности (N)
можно складывать и умножать на число,
также как матрицы. В результате получится
вектор той же размерности. Пусть имеется
несколько векторов одной
размерности x₁, x₂,…,x_K и
столько же чисел α α₁,
α₂,…,α_K.
Вектор 

y =
α₁x₁+
α₂x₂+…+
α_Kx_K  

называется линейной
комбинацией векторов x_k.

Если
существуют такие ненулевые числа α_k ≠
0, k =
1,…, K,
что y = 0,
то такой набор векторов x_k называется линейно
зависимым.
В противном случае векторы называются
линейно независимыми. Например,
векторы x₁ =
(2, 2)^t и x₂ =
(−1, −1)^t линейно
зависимы, т.к. x₁ +2x₂ = 0

Содержание 

1.13. Ранг матрицы

Рассмотрим
набор из K векторов x₁, x₂,…,x_K размерности N.
Рангом этой системы векторов называется
максимальное число линейно-независимых
векторов. Например в наборе

имеются
только два линейно независимых вектора,
например x₁ и x₂,
поэтому ее ранг равен 2. 

Очевидно,
что если векторов в наборе больше, чем
их размерность (K>N),
то они обязательно линейно зависимы. 

Рангом
матрицы (обозначается
rank(A))
называется ранг системы векторов, из
которых она состоит. Хотя любую матрицу
можно представить двумя способами
(векторы столбцы или строки), это не
влияет на величину ранга, т.к. 

rank(A)
= rank(A^t).

Содержание

1.14. Обратная матрица

Квадратная
матрица A называется
невырожденной, если она имеет
единственную обратную матрицу A^-1,
определяемую условиями

  AA⁻¹ = A⁻¹A = I.

Обратная матрица
существует не для всех матриц. Необходимым
и достаточным условием невырожденности
является 

det(A)
≠ 0 или rank(A)
= N.

Обращение матрицы
— это сложная процедура, для выполнения
которой существуют специальные программы.
Например,

Рис.
17 Обращение матрицы

Приведем формулы
для простейшего случая — матрицы 2×2

Если
матрицы A и B невырождены,
то 

(AB)⁻¹ = B⁻¹A⁻¹.

Содержание

1.15. Псевдообратная матрица

Если
матрица A вырождена
и обратная матрица не существует, то в
некоторых случаях можно
использовать псевдообратную матрицу,
которая определяется как такая матрица A⁺,
что

AA⁺A = A.

Псевдобратная
матрица — не единственная и ее вид
зависит от способа построения. Например
для прямоугольной матрицы можно
использовать метод
Мура-Пенроуза.

Если число столбцов
меньше числа строк, то 

A⁺=(A^tA)⁻¹A^t

Например, 

 

Рис.
17a Псевдообращение
матрицы

Если же число
столбцов больше числа строк, то

A⁺=A^t(AA^t)⁻¹

Содержание

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #