Как найти норму элемента в пространстве

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 июня 2021 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. норма.

Норма — функционал, заданный на векторном пространстве и обобщающий понятие длины вектора или абсолютного значения числа.

Определение[править | править код]

Норма вектора[править | править код]

Норма в векторном пространстве над полем вещественных или комплексных чисел — это функционал , обладающий следующими свойствами:

1. 
2. (неравенство треугольника);
3. 

Эти условия являются аксиомами нормы.

Векторное пространство с нормой называется нормированным пространством, а условия (1—3) — также аксиомами нормированного пространства.

Из аксиом нормы очевидным образом вытекает свойство неотрицательности нормы:

.

Действительно, из третьего свойства следует: , а из свойства 2 — .

Чаще всего норму обозначают в виде: . В частности,  — это норма элемента векторного пространства .

Вектор с единичной нормой называется единичным или нормированным.

Любой ненулевой вектор можно нормировать, то есть разделить его на свою норму: вектор имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.

Норма матрицы[править | править код]

Нормой матрицы называется вещественное число , удовлетворяющее первым трём из следующих условий:

1. , причём только при ;
2. , где ;
3. ;
4. .

Если выполняется также и четвёртое свойство, норма называется субмультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы субмультипликативны.

Матричная норма из называется согласованной с векторной нормой из и векторной нормой из если справедливо:

для всех .

Норма оператора[править | править код]

Норма оператора  — число, которое определяется так:

,

где  — оператор, действующий из нормированного пространства в нормированное пространство .

Это определение эквивалентно следующему:

• Свойства операторных норм:

1. , причём только при ;
2. , где ;
3. ;
4. .

В конечномерном случае, оператору в некотором базисе соответствует матрица — матрица оператора. Если норма на пространстве(пространствах), где действует оператор, допускает одно из стандартных выражений в базисе, то свойства нормы оператора повторяют аналогичные свойства нормы матрицы.

Свойства нормы[править | править код]

1. 
2. 
3. [косинус угла]
4. 
5. 

Эквивалентность норм[править | править код]

Примеры[править | править код]

Линейные нормированные пространства[править | править код]

• Любое предгильбертово пространство можно считать нормированным, так как скалярное произведение порождает естественную норму

где (обычно подразумевается, что это натуральное число).
В частности:

• Нормы функций в  — пространстве вещественных (или комплексных) непрерывных функций на отрезке [0,1]:

«L0 норма»[править | править код]

Особым случаем является (L0-«норма»), определяемая как количество ненулевых элементов вектора. Строго говоря, это не является нормой, так как не выполняется третья аксиома нормы. В основном таким видом «нормы» пользуются в задачах разреженного кодирования, в частности в Compressive sensing, где нужно найти наиболее разреженное представление вектора (с наибольшим количеством нулей), то есть с наименьшей -нормой. С помощью этой «нормы» может быть определенно расстояние Хэмминга.

Некоторые виды матричных норм[править | править код]

• Порожденные нормы :

Здесь  — сопряжённая к матрица,  — след матрицы.

Связанные понятия[править | править код]

Топология пространства и норма[править | править код]

Норма задаёт на пространстве метрику (в смысле — функцию расстояния метрического пространства), порождая таким образом метрическое пространство, а значит топологию, базой которой являются всевозможные открытые шары, то есть множества вида . Понятия сходимости, определённой на языке теоретико-множественной топологии в такой топологии и определённой на языке нормы, при этом совпадают.

См. также[править | править код]

• Полунорма
• Метрика
• Скалярное произведение

Примечания[править | править код]

Нормой называют
функционал 
,
удовлетворяющий следующим аксиомам:

1. 
   ,

2. 
   ,

3. 
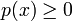
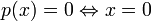
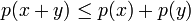
    (аксиома
   треугольника),

4. 
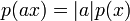
    для
   любого числа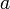 
    (абсолютная
   однородность).

Таким
образом, норма – это полунорма, на которую
наложено дополнительное условие: норма
равна нулю только на нулевом элементе.

Нормированным
пространством называют
линейное пространство с заданной на
нём нормой.

Норму
элемента линейного пространства 
 обозначают 
.

Полное
нормированное пространство
называется банаховым
пространством.

Евклидово
пространство.
Скалярным произведением в
действительном линейном
пространстве 
 называется
функционал от двух переменных 
,
определённый для любых 
 и
удовлетворяющий следующим аксиомам:

1. 
   ,

2. 
   ,

3. 
   ,

4. 
   ,

5. 
   .

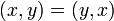
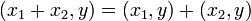
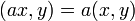
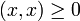
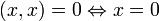
Евклидово
пространство —
это линейное пространство с заданным
в нём скалярным произведением.

В
евклидовом пространстве норма естественным
образом определяется через скалярное
произведение:

Ортогонализация —
это процесс построения ортонормированной
системы на основе линейно независимой
системы векторов.

Теорема
1 (Об ортогонализации). Рассмотрим
линейно независимую систему

элементов
евклидова пространства 
.
В пространстве 
 существует
ортогональная система элементов

,
причём каждый элемент 
 есть
линейная комбинация вида

,каждый
элемент 
 представляется
в виде
,при
этом, каждый элемент 
 определяется
с точностью до множителя 
.

Вопрос 9. Матрицы и основные действия над матрицами. Свойства действий над матрицами.

  Матрица
может состоять как из одной строки, так
и из одного столбца. Вообще говоря,
матрица может состоять даже из одного
элемента.

Определение. Если
число столбцов матрицы равно числу
строк (m=n), то матрица называетсяквадратной.

Определение. 
Матрица вида:= E,называется единичной
матрицей.

 Определение. Если a_mn = a_nm ,
то матрица называется симметрической.

Определение. Квадратная
матрица вида  называется диагональной матрицей.

Сложение
и вычитание матриц
сводится к соответствующим операциям
над их элементами. Самым главным свойством
этих операций является то, что
они определены
только для матриц одинакового размера.
Таким образом, возможно определить
операции сложения и вычитания матриц:

Определение. Суммой
(разностью) матриц
является матрица, элементами которой
являются соответственно сумма (разность)
элементов исходных матриц.

c_ij = a_ij  b_ij
С = А + В = В + А.

Операция умножения
(деления) матрицы
любого размера на произвольное число
сводится к  умножению (делению) каждого
элемента матрицы на это число.

 (А+В)
=А  В
А() = А  А 

Операция
умножения матриц

Определение: Произведением матриц
называется матрица, элементы которой
могут быть вычислены по следующим
формулам: AB = C;

Из
приведенного определения видно, что
операция умножения матриц определена
только для матриц, число
столбцов первой из которых равно числу
строк второй.

Свойства
операции умножения матриц. 

1)Умножение
матриц не
коммутативно,
т.е. АВ  ВА
даже если определены оба произведения.
Однако, если для каких – либо матриц
соотношение АВ=ВА выполняется, то такие
матрицы называютсяперестановочными.

Самым
характерным примером может служить
единичная матрица, которая является
перестановочной с любой другой матрицей
того же размера.

Перестановочными
могут быть только квадратные матрицы
одного и того же порядка.

АЕ
= ЕА = А

Очевидно,
что для любых матриц выполняются
следующее свойство: AO = O;  OA = O,

где
О – нулевая матрица.

 2)
Операция перемножения матриц ассоциативна, т.е.
если определены произведения АВ и (АВ)С,
то определены ВС и А(ВС), и выполняется
равенство: (АВ)С=А(ВС). 

3)
Операция умножения матриц дистрибутивна по
отношению к сложению, т.е. если имеют
смысл выражения  А(В+С) и (А+В)С, то
соответственно: А(В + С) = АВ + АС

(А
+ В)С = АС + ВС.

4)
Если произведение АВ определено, то для
любого числа  верно
соотношение: (AB)
= (A)B = A(B). 

5)
Если определено произведение АВ , то
определено произведение В^ТА^Т и
выполняется равенство:(АВ)^Т =
В^ТА^Т,
где индексом Т обозначается транспонированная матрица.

 6)
Заметим также, что для любых квадратных
матриц det (AB) = detAdetB.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Теперь дадим основное

Определение 1. Пусть X — линейное пространство над полем действительных или комплексных чисел.

Функция ставящая каждому вектору в соответствие действительное число называется нормой в линейном пространстве X, если она удовлетворяет следующим трем условиям:

(невырожденность);

(однородность);

(неравенство треугольника).

Определение 2. Линейное пространство с определенной на нем нормой называется линейным нормированным пространством.

Определение 3. Значение нормы на векторе называется нормой этого вектора.

Норма вектора всегда неотрицательна (и, как видно из а), равна нулю только для нулевого вектора).

Действительно, для любого в силу с) и с учетом а) и получаем

Из с) и принципа индукции следует общее неравенство

а с учетом b) из с) легко вывести также полезное неравенство

Любое линейное нормированное пространство имеет естественную метрику

То, что так определенная функция удовлетворяет аксиомам метрики, непосредственно следует из свойств нормы.

Благодаря наличию в X линейной структуры метрика в X обладает двумя дополнительными специфическими свойствами:

т. е. метрика инвариантнаотносительно переносов, и

т. е. она однородна.

Определение 4. Если линейное нормированное пространство является полным как метрическое пространство относительно естественной метрики (3), то оно называется полным нормированным пространством или банаховым пространством.

Пример 5. Если для вектора при положить

то, как следует из неравенства Минковского, мы получим норму в Пространство наделенное этой нормой, будем обозначать символом

Можно проверить, что

и что

при Таким образом, естественно положить

Тогда из (4) и (5) следует, что

Из этого неравенства, как, впрочем, и из самого определения (4) нормы видно, что является полным нормированным пространством.

Пример 6. Предыдущий пример полезно обобщить следующим образом. Если есть прямое произведение нормированных пространств, то в X можно ввести норму вектора

положив

где есть норма вектора пространстве

Естественно, неравенства (8) и в этом случае остаются в силе. В дальнейшем, когда рассматривается прямое произведение нормирований пространств, всегда, если нет специальных оговорок, предполагается, что в нем норма определена в соответствии с формулой (9) (включая случай

Пример 7. Пусть 1. Обозначим через множество таких последовательностей действительных или комплексных чисел, что ряд сходится, и для положим

Используя неравенство Минковского, легко видеть, что является линейным нормированным пространством относительно стандартных линейных операций и нормы (10). Это бесконечномерное пространство, по отношению к которому является линейным подпространством конечной размерности.

Для нормы (10) справедливы все неравенства (8), кроме последнего. Нетрудно проверить, что является банаховым пространством.

Пример 8. В линейном пространстве числовых функций, непрерывных на отрезке чаще всего рассматривается следующая норма:

Проверку аксиом нормы мы оставляем читателю. Заметим, что эта норма порождает уже знакомую нам метрику (см. гл. IX, § 5) на и нам известно, что возникающее при этом метрическое пространство полно. Таким образом, линейное пространство с нормой (11) является банаховым.

Пример 9. В можно ввести и иную норму

которая сводится к (11) при

Легко видеть (см., например, гл. IX, § 5), что при пространство с нормой (12) не является полным.

Пусть в линейном пространстве $ mathbb V_{} $ определена функция, которая ставит в соответствие каждому вектору $ X subset mathbb V $ вещественное число, называемое нормой
вектора¹⁾ $ X_{} $, и обозначаемое $ | X | $; при этом функция
подчиняется аксиомам:

1.

если $ | X |= 0 $, то $ X=mathbb O $;

2.

$ | X + Y | le |X | + |Y | $ для $ forall { X, Y } subset mathbb V $ (неравенство треугольника);

3.

$ | alpha , X |=|alpha |cdot | X | $ для $ forall X in mathbb V $ и $ forall alpha in mathbb R $ если пространство вещественно и
$ forall alpha in mathbb C $ если оно комплексно (однородность нормы).

Пространство $ mathbb V $ с введенной в нем нормой называется нормированным (линейным) пространством.

Из этих аксиом вытекает следующее свойство нормы, которое часто включают в состав аксиом.

Т

Теорема. Любая норма должна быть неотрицательной функцией:
$$ | X | ge 0 quad npu quad forall Xin mathbb V , . $$

Доказательство. Действительно, из аксиомы

3

вытекает, что норма нулевого вектора должна быть равна $ 0_{} $:
$$ | mathbb O | = | 0 cdot mathbb O |= 0 | mathbb O | = 0 , . $$
Из аксиом

2

и

3

тогда следует:
$$ 0= | mathbb O | = | X-X |le | X| +|-X |= 2 |X | quad npu quad forall X in mathbb V . $$

♦

В широком классе вещественных пространств норма может быть введена естественным образом.

Т

Теорема. Любое евклидово пространство $ mathbb E $ является нормированным пространством.

Действительно введем в пространстве $ mathbb E $ норму как длину вектора:
$$ | X | = sqrt{langle X, X rangle } , . $$
Аксиомы скалярного произведения гарантируют выполнение аксиом нормы.

Тем не менее, норму можно вводить и независимо от скалярного произведения.

Нормированные пространства включают в себя евклидовы пространства, но не сводятся к последним.

В пространстве $ mathbb R^n $ вещественных векторов-строк $ X=(x_1,dots,x_n) $ евклидова норма определяется
$$ |X|_2 = sqrt{x_1^2+dots+ x_n^2} , . $$
Это определение можно считать частным случаем из целого класса гёльдеровых норм
$$
|X|_p=left( |x_1|^p+dots+|x_n|^p right)^{1/p}
$$
при $ p in mathbb N $. Эта норма называется также $ p $-нормой или $ ell_p $-нормой. Она, очевидно может быть распространена и на случай комплексного пространства $ mathbb C^n $.

Норма $ ell_1 $
$$ |X|_1 = |x_1|+dots+|x_n| $$
называется еще манхэттенской нормой.

При переходе в $ p $-норме к пределу при $ p to + infty $ получаем бесконечную норму
$$ |X|_{infty}= max_{jin {1,dots,n}} |x_j| , . $$

П

Пример. Для $ X=(1,-2,3,4) $ имеем:

$$ |X|_1=10, |X|_2=sqrt{30} approx 5.477226, |X|_3=sqrt[3]{100} approx 4.641588, dots, |X|_{infty}=4 , . $$

Различные способы задания нормы в одном и том же линейном пространстве порождают различные формы окрестности вектора (точки) этого пространства. Для примера изобразим $ 1 $-окрестность начала координат в $ mathbb R^2 $ (“единичный круг”):

?

А вот при $ 0<p<1 $ и $ n>1 $ формула $ |X|_p $ норму не задает! Почему? — Посмотрите на форму астроиды.

Т

Теорема. Любая норма является выпуклой функцией на любом выпуклом подмножестве пространства $ mathbb V $.

Действительно, на основании аксиом

2

и

3

для нормы выполняется неравенство Йенсена.

В пространстве $ mathbb P_n $ полиномов с вещественными коэффициентами степеней, не превышающих $ n $ скалярное произведение может определяться как посредством скаярного произведения векторов коэффициентов, так и формулой
$$
langle f(x), g(x) rangle = int_{a}^b f(t)g(t) d,t
$$
при некоторых фиксированных вещественных константах $ a_{} $ и $ b_{} $, $ a_{}<b $. Последний случай порождает определение нормы полинома
$$ |f(x)| = left(int_{a}^b f^2(t) d,t right)^{1/2} , . $$
Эта последняя распространяется на бесконечномерное пространство функций, которое обозначается $ mathbf L^2 $.

Любую матрицу $ A $ порядка $ m times n $ с вещественными или комплексными элементами можно векторизовать, т.е. считать ее вектором из $ mathbb R^{mn} $ или из $ mathbb C^{mn} $. Любая норма, введенная в этих пространствах, породит и норму в линейном пространстве матриц.

П

Пример 1.
Для матрицы $ Ain mathbb C^{mtimes n} $ евклидова норма или норма Фробениуса вводится формулой:

$$| A |_F = sqrt{sum_{j,k} |a_{jk}|^2} .$$
С использованием операции вычисления следа матрицы, эту формулу для вещественных матриц можно переписать в виде
$$
| A |_F = sqrt{ operatorname{Sp}_{}, (A cdot A^{^{top}})}= sqrt{ operatorname{Sp}_{}, (A^{^{top}}A)} , .
$$

♦

Т

Теорема. Евклидова норма вещественной матрицы не меняется при умножении этой матрицы на произвольную ортогональную.

Доказательство. Имеем:
$$ |A |_F= operatorname{Sp}_{}, (A cdot A^{^{top}}) , . $$
Пусть $ Q in mathbb R^{mtimes m} $ — ортогональная матрица, тогда
$$ |QA |_F= operatorname{Sp}_{}, (QA cdot A^{^{top}} Q^{^{top}}) = $$
и на основании свойства следа $ operatorname{Sp}(A_1 A_2)=operatorname{Sp} (A_2 A_1) $ для квадратных матриц $ A_1 $ и $ A_2 $:
$$ = operatorname{Sp}_{}, (A cdot A^{^{top}} Q^{^{top}}Q) = operatorname{Sp}_{}, (A cdot A^{^{top}} E) = |A |_F $$
поскольку матрица $ Q $ — ортогональная. Аналогично доказывается утверждение теоремы при умножении матрицы $ A $ справа на ортогональную матрицу $ P in mathbb R^{ntimes n} $.

♦

Аналоги гёльдеровых норм $ | cdot |_1 $ и $ | cdot |_{infty} $ кажутся очевидными:
$$ sum_{j,k} |a_{jk}| quad u quad max_{j,k} |a_{jk}| $$
соответственно.
Однако по некоторым соображениям, приведенным ниже, эти аналоги вводят другими способами.

Суммируем модули элементов матрицы по столбцам и выбираем максимальное из полученных чисел:
$$ | A |_1 = max_{kin {1,dots,n}} sum_{j=1}^m |a_{jk}| , . $$
Для матрицы, состоящей из одного столбца, получим норму $ | cdot |_1 $ в $ mathbb C^m $.

Теперь суммируем модули элементов матрицы по строкам и выбираем максимальное из полученных чисел:
$$ displaystyle | A |_{infty} = max_{jin {1,dots,m}} sum_{k=1}^n |a_{jk}| , . $$
Для матрицы, состоящей из одного столбца, получим норму $ | cdot |_{infty} $ в $ mathbb C^m $.

Для матриц имеется еще одна операция: их можно умножать. Ввести эту операцию можно разными способами, но мы ограничимся самым распространенным. При умножении матрицы на столбец:
$$ A_{mtimes n} X_{ntimes 1} $$
получаем вектор-столбец $ Y_{mtimes 1} $. Как связаны между собой нормы матрицы $ A $ и столбцов $ X $ и $ Y $? В каждом из этих пространств $ mathbb C^{mtimes n} $, $ mathbb C^{n} $ и $ mathbb C^{m} $ нормы могут быть определены произвольным образом. Желательно их как-то согласовать. С этой целью (а также имея в виду некоторые приложения) для норм матриц вводят еще одну аксиому (в дополнение к основным аксиомам):

4.

Для произвольных матриц $ A $ и $ B $, для которых определено произведение $ A cdot B $, должно быть выполнено неравенство
$$ |A cdot B | le |A | cdot | B | , . $$

П

Пример 2. Эта аксиома сразу же блокирует желание выбора в качестве кандидата нормы $ max_{j,k} |a_{jk}| $:

$$
left( begin{array}{cc} 1 & 1 \ 0 & 1 end{array} right)^2 =
left( begin{array}{cc} 1 & 2 \ 0 & 1 end{array} right) , .
$$

♦

Применение аксиомы

4

к произведению матрицы на столбец приводит к следующему:
$$ |AX|le |A | cdot |X| quad Rightarrow quad frac{|AX|}{|X|} le |A| quad npu quad forall X in mathbb C^n, Xne mathbb O_{ntimes 1} , . $$
При заданных нормах столбцов в $ mathbb C^n $ и $ mathbb C^m $ получили условие на норму матрицы. А теперь зададим эту норму условием минимально допустимой жёсткости
$$
|A|=max_{Xne mathbb O} frac{|AX|}{|X|}
$$
и посмотрим к чему это приведет (если приведет — достижимость $ max $ еще нужно доказывать!). Забегая вперед, дадим определение: таким образом вводимая норма матрицы $ A $ называется матричной нормой, подчиненной векторным нормам в $ mathbb C^n $ и $ mathbb C^m $ (или индуцированной²⁾ этими последними).

П

Пример 3. В пространстве $ mathbb R^{3times 2} $ рассмотрим норму $ | cdot |_1 $. Пусть, для определенности, для ненулевой матрицы $ A $ справедливо:

$$ | A|_{1}= max (|a_{11}|+|a_{21}|+|a_{31}|, |a_{12}|+|a_{22}|+|a_{32}| )=|a_{11}|+|a_{21}|+|a_{31}| , . $$
Имеем для любого ненулевого вектора $ (x_1,x_2) subset mathbb R^2 $:

$$
L(x_1,x_2)=frac{|a_{11}x_1+a_{12}x_2|+|a_{21}x_1+a_{22}x_2|+|a_{31}x_1+a_{32}x_2|}{|x_1|+ |x_2| }le
$$
$$
le frac{|a_{11}|cdot |x_1|+|a_{12}| cdot |x_2|+|a_{21}|cdot |x_1|+|a_{22}|cdot |x_2|+|a_{31}| cdot|x_1|+|a_{32}| cdot |x_2|}{|x_1|+ |x_2| }=
$$
$$
=frac{(|a_{11}|+|a_{21}|+|a_{31}|)|x_1|+(|a_{12}|+|a_{22}|+|a_{32}|)|x_2|}{|x_1|+ |x_2|}
$$
$$
le frac{(|a_{11}|+|a_{21}|+|a_{31}|)(|x_1|+|x_2|)}{|x_1|+ |x_2|}=|a_{11}|+|a_{21}|+|a_{31}| , .
$$
В то же время, при $ x_1 ne 0 $ имеем
$$ L(x_1,0)=|a_{11}|+|a_{21}|+|a_{31}| , $$
т.е. $ max L(x_1,x_2) $ достижим. Матричная норма $ | cdot |_{1} $ является подчиненной для норм $ | cdot |_{1} $, введенных в пространствах векторов-столбцов $ mathbb R^2 $ и $ mathbb R^3 $.

♦

П

Пример 4. В пространстве $ mathbb R^{3times 2} $ рассмотрим норму $ | cdot |_{infty} $. Пусть, для определенности, для ненулевой матрицы $ A $ справедливо:

$$ | A|_{infty}= max (|a_{11}|+|a_{12}|, |a_{21}|+|a_{22}|, |a_{31}|+|a_{32}| )=|a_{11}|+|a_{12}| , . $$
Имеем для любого ненулевого вектора $ (x_1,x_2) subset mathbb R^2 $:

$$
frac{max(|a_{11}x_1+a_{12}x_2|,|a_{21}x_1+a_{22}x_2|,|a_{31}x_1+a_{32}x_2|)}{max( |x_1|, |x_2|) }le
$$
$$
le frac{max(|a_{11}|cdot |x_1|+|a_{12}|cdot |x_2|,|a_{21}|cdot |x_1|+|a_{22}|cdot |x_2|,|a_{31}|cdot |x_1|+|a_{32}|cdot| x_2|)}{max( |x_1|, |x_2|) }le
$$
$$
le frac{max((|a_{11}|+|a_{12}|)max( |x_1|, |x_2|),(|a_{21}|+|a_{22}|)max( |x_1|, |x_2|),|a_{31}|+|a_{32}|)max( |x_1|, |x_2|))}{max( |x_1|, |x_2|) }le
$$
$$
le max (|a_{11}|+|a_{12}|, |a_{21}|+|a_{22}|, |a_{31}|+|a_{32}| )=|a_{11}|+|a_{12}| , .
$$
С другой стороны, для $ widetilde x_1=operatorname{sign} (a_{11}), widetilde x_2=operatorname{sign} (a_{12}) $ получаем
$$ max ( |a_{11}widetilde x_1+a_{12} widetilde x_2|,|a_{21}widetilde x_1+a_{22} widetilde x_2|,|a_{31}widetilde x_1+a_{32} widetilde x_2| )
=
$$
$$
=
max ( |a_{11}|+|a_{12}|,|a_{21}widetilde x_1+a_{22} widetilde x_2|,|a_{31}widetilde x_1+a_{32} widetilde x_2| ) ge |a_{11}|+|a_{12}| , .
$$
Из двух выведенных неравенств следует, что матричная норма $ | cdot |_{infty} $ является подчиненной для норм $ | cdot |_{infty} $, введенных в пространствах векторов-столбцов $ mathbb R^2 $ и $ mathbb R^3 $.

♦

А вот с евклидовыми нормами ситуация оказывается посложнее…

П

Пример 5. Пусть в пространствах векторов-столбцов $ mathbb R^{m} $ и $ mathbb R^{n} $ заданы евклидовы нормы

$$ | (y_1,dots,y_m)^{top} |=sqrt{y_1^2+dots+y_m^2}, | (x_1,dots,x_n)^{top} |=sqrt{x_1^2+dots+x_n^2} , . $$
Тогда
$$ |AX|_{2} = sqrt{X^{^{top}}A^{^{top}} A X} $$
и
$$
frac{|AX|_2}{|X|_2}=sqrt{frac{X^{^{top}}A^{^{top}} A X}{X^{^{top}}X}} , .
$$
Матрица $ A^{^{top}} A $ является симметричной и положительно полуопределенной, т.е. все ее собственные числа неотрицательны. По доказанному в

☞

ПУНКТЕ, подкоренное выражение имеет максимальное значение равное максимальному собственному числу
матрицы $ A^{^{top}} A $. В результате, матричную спектральную норму³⁾ $ |cdot |_2 $ определяют равенством:
$$ |A|_2=sigma_{max} $$
где $ sigma_{max} $ означает максимальное сингулярное число матрицы $ A $.

Для матрицы $ A $, состоящей из одного столбца $ A=(a_1,dots,a_m)^{^{top}} $, матрица $ A^{^{top}} A =a_1^2+dots+a_m^2 $. Следовательно,
$$ sigma_{max} =sqrt{a_1^2+dots+a_m^2} , $$
и спектральная матричная норма совпадает с евклидовой нормой в $ mathbb R^m $.

Таким образом, спектральная матричная норма $ | cdot |_2 $ оказывается подчиненной евклидовой векторной норме $ | cdot |_2 $.

♦

В терминах сингулярных чисел матрицы $ A $ норму Фробениуса $ | A |_{F} $ из примера $ 1 $ можно записать в виде
$$ | A |_{F}= sqrt{sum_{j} sigma_j^2} , $$
где суммирование идет по квадратам всех сингулярных чисел матрицы $ A $. Из этого замечания следуют очевидные неравенствв:
$$ | A |_2 le | A |_{F} le sqrt{mathfrak r} | A |_2 quad npu forall A, operatorname{rank} A = mathfrak r , . $$

?

Доказать, что равенство в левом неравенстве достигается тогда и только тогда когда $ mathfrak r le 1 $.

П

Пример 6. Для

$$
A=
left(begin{array}{rr}
3 & -2 \
1 & 1 \
-5 & 1
end{array}
right)
$$
имеем

$$
|A|_F= sqrt{9+4+1+1+25+1}=sqrt{41} approx 6.4031,
$$
$$
|A|_1 = max {3+1+5, 4+1+1} = 9, |A|_{infty} = max {3+2, 1+1, 5+1}=6
$$
Для нахождения $ |A|_2 $ вычисляем
$$
A^{^{top}} A =
left(
begin{array}{rr}
35 & -10 \
-10 & 6
end{array}
right) , .
$$
Характеристический полином $ det (A^{^{top}} A-lambda E) equiv lambda^2-41, lambda+ 110 $ имеет корни
$$ lambda_1=frac{41+sqrt{1241}}{2}, lambda_2=frac{41-sqrt{1241}}{2} $$
и $ |A|_2 =sqrt{lambda_1} approx 6.173647 $.

♦

С вычислительной точки зрения спектральная норма $ | cdot |_2 $ наиболее «дорогая»: она требует вычисления собственного числа матрицы. К счастью, как правило, можно организовать это вычисление без промежуточного вычисления характеристического полинома. В самом деле, для приближенного вычисления максимального собственного числа положительно полуопределенной симметричной матрицы $ A^{^{top}} A $ можно воспользоваться методом степенных итераций.

?

Верно ли равенство $ |A^{-1}|= |A|^{-1} $ для квадратной невырожденной матрицы $ A $?

Т

Теорема [Шур]. Для спектра $ {lambda_1,dots,lambda_n} $ квадратной матрицы $ A in mathbb R^{ntimes n} $ имеют место неравенства

$$ sqrt{sum_{j=1}^n |lambda_j|^2} le |A|_{_F} ; $$

$$ sqrt{sum_{j=1}^n | mathfrak{Re} (lambda_j)|^2} le left|frac{1}2(A+A^{top})right|_{_F} ; $$

$$ sqrt{sum_{j=1}^n | mathfrak{Im} (lambda_j)|^2} le left|frac{1}2(A-A^{top})right|_{_F} . $$