Matrix norm
| [1-6] /6 | Disp-Num |
|
- Purpose of use
- Homework check
[1] 2022/10/16 08:40 20 years old level / High-school/ University/ Grad student / Useful /
- Purpose of use
- To double-check my L2 norm calculations.
- Bug report
- Incoorect L2 norm computed for the following matrix:
2 -1 0 0
-1 2 -1 0
0 -1 2 -1
0 0 -1 2Maximum eigenvalue for this symmetric matrix is 3.61803398875
Not 2.61803398875, as calculated here. - from Keisan
- Thank you for your advice.
We’ve fixed the bug.
[2] 2019/12/09 04:44 20 years old level / High-school/ University/ Grad student / Useful /
- Purpose of use
- Learn L2 norm
[3] 2019/10/15 02:31 20 years old level / High-school/ University/ Grad student / Very /
- Purpose of use
- homework check
[4] 2019/10/01 22:09 Under 20 years old / High-school/ University/ Grad student / Very /
- Purpose of use
- learning how to norm matrix for my work.
The examples helps
[5] 2019/08/18 06:44 40 years old level / An office worker / A public employee / A little /
- Bug report
- The text definition of the L2 norm is incorrect. The calculated result is correct though.
Is says it”s the maximum eigenvalue of A, that is lambda_max(A).
Instead it should say that it”s the largest spectral radius, that is sigma_max(A).
Equivalently that”s the largest eigenvalue of A^T.A (or A^* A for complex matrices).
See e.g. https://en.wikipedia.org/wiki/Matrix_norm - from Keisan
- Thank you for your advice.
We have fixed it.
[6] 2018/01/19 20:51 50 years old level / An engineer / Useful /

Thank you for your questionnaire.
Sending completion
To improve this ‘Matrix norm Calculator’, please fill in questionnaire.
Нормы матриц часто используются при определении погрешности различных численных методов. В частности, в итерационных методах решения систем линейных алгебраических уравнений они применяются для того, чтобы определить погрешность решения, найденного на каждой итерации.
Как правило, используются нормы трех видов.
1) M-норма. Вычисляется по формуле

Пример.Для матрицы 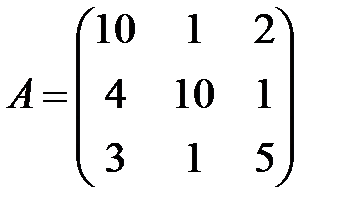
2) L-норма. Вычисляется по формуле

Пример.Для матрицы 
3) K-норма. Вычисляется по формуле
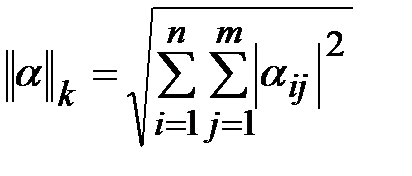
Пример.Для матрицы
k-норма равна
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8444 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Рассмотрим произвольную матрицу A порядка m×n и связанную с нею линейное преобразование y=Ax, где x∈V n , y∈U m . Введем в этих пространствах нормы векторов 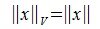
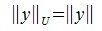
Определим норму матрицы A равенством:
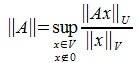 |
(1) |
Из определения нормы матрицы следует:
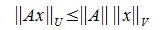 |
(2) |
Пусть для двух матриц A и B порядка m×n определены одни и те же векторные нормы. Тогда имеем соотношение:
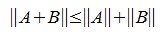 |
(3) |
Кроме того справедливо равенство
где λ любое число.
Пусть для m×n матрицы A и n×k матрицы B определены матричные нормы 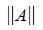
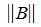
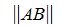
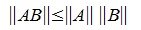
Вычислим норму матрицы A , введя в пространствах V и U конкретные векторные нормы.
1. Пусть в пространствах V и U введена векторная норма
В (5) и (6) неравнетство превращается в равенство, если взять 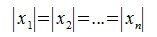
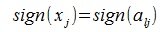
достигает своего максимума. Учитывая высшеизложенное, неравенство (6) и равенство (1), получим:
2. Введем в пространствах V и U векторную норму
Пусть 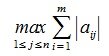
Учитывая (1),(8) и (9) получим l-норму матрицы A:
Норму матрицы, определяемую с помощью формулы (1), называется операторной нормой, подчиненной данной норме векторов.
Отметим, что определение нормы матрицы (1) эквивалентно следующему определению:
Действительно, любой ненулевой вектор x∈V можно представить в виде произведения λx₁, где 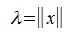
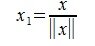
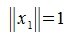
Примеры вычисления нормы матрицы
Вычислим m-норму и l-норму матрицы используя (7) и (10).
Геометрическая интерпретация нормы матрицы
Пусть в линейном пространстве V введена m-норма для всех векторов x∈V:

Найдем норму матрицы
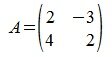
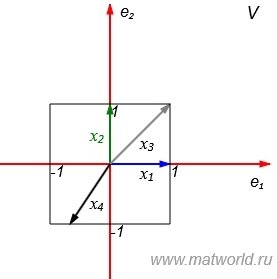
Рассмотрим множество всех векторов, которые имеют норму 1. В двухмерном пространстве это те векторы конечные точки которых находятся на квадрате на рис. 1. Обозначим это множество символом X.
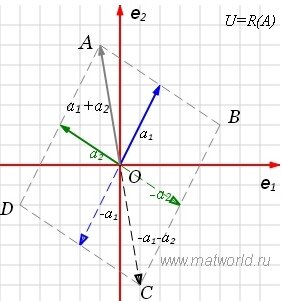
На рисунке рис. 2 изображено пространство столбцов матрицы A. Каждому вектору x∈X соответствует вектор Ax в U. Конечные точки этих векторов находятся на пунктирном четырехугольнике ABCD. m-норма матрицы A – это модуль наибольшго координата наибольшего из векторов, конечная точка которого находится на четырехугольнике ABCD. На рис.2 это векторы 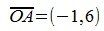
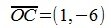
Отметим, что норма матрицы показывает насколько максимально растягивается вектор x при отображении y=Ax. В нашем примере векторы х растягиваются максимально 6 раз.
Программированию нельзя научить, можно только научится
Главная » Уроки по Численным методам » Урок 12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц
Если все миноры матрицы Aпорядка kравны нулю, то все миноры порядка k+1, если такие существуют, тоже равны нулю.
Рангом матрицы A называется наибольший из порядков миноров матрицы A, отличных от нуля.
Максимум ранг может быть равен минимальному числу из количества строк или столбцов матрицы, т.е. если матрица имеет размер 4х5, то максимум ранг будет 4.
Минимум ранг матрицы равен 1, если только вы не имеете дело с нулевой матрицей, там всегда ранг равен нулю.
Ранг невырожденной квадратной матрицы порядка n равен n, так как ее определитель является минором порядка n и у невырожденной матрицы отличен от нуля.
При транспонировании матрицы ее ранг не меняется.
Пусть ранг матрицы равен 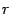
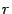
Пример. Дана матрица А. 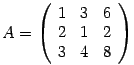
Определитель матрицы 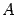
Минор второго порядка 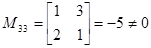
Базисным минором является также минор 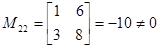
Минор 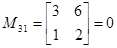
Задание: самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
При элементарных преобразованиях ранг матрицы не меняется.
Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.
Пусть требуется вычислить ранг матрицы 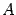
- С помощью перестановки строк и столбцов матрицы добиваемся того, чтобы в левом верхнем углу матрицы стоял ненулевой элемент. Итак, считаем, что
. Первую строку оставляем без изменений.
- Ко второй строке прибавляем первую, умноженную на число
.
- К третьей строке прибавляем первую строку, умноженную на число
.
- Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке. В результате получим матрицу А1, в которой в первом столбце все элементы равны 0, кроме элемента
.
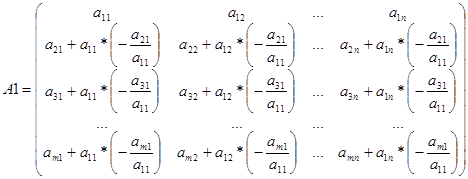
В результате расчетов матрица А1 имеет вид
- Если все строки, начиная со второй, в полученной матрице нулевые, то ее ранг равен 1, так как есть минор первого порядка, отличный от нуля
. В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что
.
- Первую и вторую строки оставляем без изменений.
- К третьей строке прибавляем вторую, умноженную на число
. В результате получим, что второй элемент третьей строки равен нулю.
- Затем к четвертой строке прибавляем вторую, умноженную на число
, и т.д. В результате получаем матрицу
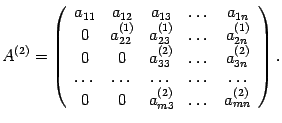
Если все строки, начиная с третьей, нулевые, то 

На каком-то этапе мы придем к матрице, у которой все строки, начиная с (r+1)-ой , равны нулю (или отсутствуют при 



В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.
Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.
В лабораторно-практической работе рассмотрим пример нахождения ранга матрицы.
АЛГОРИТМ НАХОЖДЕНИЯ НОРМЫ МАТРИЦЫ.
Выделяют всего три нормы матрицы.
Первая норма матрицы = максимальному из чисел, полученных при сложении всех элементов каждого столбца, взятых по модулю.
Пример: пусть дана матрица А размера 3х2 (рис.10). В первом столбце стоят элементы: 8, 3, 8. Все элементы положительные. Найдем их сумму: 8+3+8=19. Во втором столбце стоят элементы: 8, -2, -8. Два элемента – отрицательные, поэтому при сложении этих чисел, необходимо подставлять модуль этих чисел (т.е. без знаков “минус”). Найдем их сумму: 8+2+8=18. Максимальное из этих двух чисел – это 19. Значит первая норма матрицы равна 19.

Рисунок 10.
Вторая норма матрицы представляет из себя квадратный корень из суммы квадратов всех элементов матрицы. А это значит мы возводим в квадрат все элементы матрицы, затем складываем полученные значения и из результата извлекаем квадратный корень.
В нашем случае, 2 норма матрицы получилась равна квадратному корню из 269. На схеме, я приближенно извлекла квадратный корень из 269 и в результате получила приблизительно около 16,401. Хотя более правильно не извлекать корень.
Третья норма матрицы представляет из себя максимальное из чисел, полученных при сложении всех элементов каждой строки, взятых по модулю.
В нашем примере: в первой строке стоят элементы: 8, 8. Все элементы положительные. Найдем их сумму: 8+8=16. В второй строке стоят элементы: 3, -2. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 3+2=5. В третьей строке стоят элементы 8, и -8. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 8+8=16. Максимальное из этих трех чисел – это 16. Значит третья норма матрицы равна 16.
Численные методы линейной алгебры
Основные положения численного анализа
Классическим средством изучения математических моделей и исследований на их основе свойств реальных объектов являются аналитические методы, позволяющие получать точные решения в виде математических формул. Эти методы дают наиболее полную информацию о решении задачи, и они до настоящего времени не утратили своего значения. Однако, к сожалению, класс задач, для которого они могут использоваться, весьма ограничен. Поэтому решение, как правило, осуществляется численными методами.
Численные методы — это методы приближенного решения задач прикладной математики, основанные на реализации алгоритмов, соответствующих математическим моделям. Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой. Численные методы, в отличие от аналитических, дают не общие, а частные решения. При этом требуется выполнить достаточное количество арифметических и логических действий над числовыми и логическими массивами.
В численном анализе используются два класса численных методов:
1. Прямые методы, позволяющие найти решение за определенное число операций.
2. Итерационные методы, основанные на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию.
Решения, получаемые численными методами, в силу их приближенности содержат некоторые погрешности. Рассмотрим их источники и типы.
Один из типов погрешностей обусловлен неадекватностью выбранной математической модели исходной физической. Эта неадекватность в большей или меньшей степени присуща всем приближенно решаемым задачам. Данная погрешность является неустранимой. Неточность (неопределенность) задания исходных данных приводит также к неустранимым погрешностям.
Если мы устраним неопределенность в исходных данных и найдем решение с помощью какого-либо численного метода, то получим результат, не в точности соответствующий исходным данным в силу погрешности численного метода. В компьютере все числа представляются в конечном виде, и поэтому при использовании вычислительного алгоритма реализуются ошибки арифметических и других операций над числами, а также ошибки округления.
Дадим некоторые понятия из теории погрешностей вычислительных действий над приближенными величинами.
Пусть [math]x[/math] — точное, но, как правило, неизвестное значение некоторой величины, а [math]widehat{x}[/math] — ее известное приближенное значение.
Абсолютной погрешностью приближения [math]widehat{x}[/math] называется разность [math]Delta=bigl|x-widehat{x}bigr|[/math] (в общем случае [math]Deltawidehat{x}[/math] имеет размерность величины [math]x[/math]).
Относительная погрешность приближения [math]widehat{x}[/math] обозначается [math]delta[/math] и выражается отношением [math]delta= frac{Deltawidehat{x}}{|widehat{x}|}[/math] ([math]delta[/math] — безразмерная величина, [math]widehat{x}ne0[/math]). Часто величина [math]delta[/math] вычисляется в процентах, и тогда она умножается на сто.
Так как величина [math]x[/math], как правило, неизвестна, а погрешность необходимо определять, то в рассмотрение вводится предельная абсолютная погрешность [math]Delta(widehat{x}):[/math]
[math]Deltawidehat{x}= |x-widehat{x}|leqslant Delta(widehat{x}).[/math]
Раскрывая в этом неравенстве модуль, получаем соотношение, задающее отрезок, которому принадлежит точное значение: [math]widehat{x}-Delta(widehat{x}) leqslant xleqslant Delta(widehat{x})[/math]. Таким образом, величина [math]x[/math] находится в ∆-окрестности (дельта-окрестности), определяемой величинами [math]widehat{x}[/math] и [math]Delta(widehat{x})[/math].
Предельная относительная погрешность приближения [math]widehat{x}[/math] определяется отношением [math]delta(widehat{x})= frac{Delta(widehat{x})}{|widehat{x}|}[/math].
Такие погрешности оцениваются при рассмотрении численных методов. Эти оценки могут производиться до выполнения вычислений (априорные оценки) и после них (апостериорные оценки).
Как правило, численный алгоритм решения задачи завершается, если погрешность меньше заданной заранее величины.
Норма матриц: понятие, определение, примеры
При решении многих практических задач необходимо как-то “измерять” матрицы, чтобы говорить, что одна матрица больше другой. Правило, по которому матрице (в частности, матрице-столбцу) ставится в соответствие некоторое неотрицательное число, имеющее смысл меры, определяет понятие норма матрицы.
Нормой матрицы-столбца [math]x=begin{pmatrix}x_1\vdots\x_nend{pmatrix}[/math] называется функция [math]|x|[/math], удовлетворяющая следующим аксиомам:
1. [math]|x|geqslant0[/math] для любого столбца [math]x[/math], причем [math]|x|=0[/math] в том и только в том случае, если [math]x[/math] — нулевой столбец;
2. [math]|alpha x|=|alpha|cdot|x|[/math] для любого действительного числа [math]alpha[/math];
3. [math]|x+y|leqslant|x|+|y|[/math] для любых двух столбцов [math]x[/math] и [math]y[/math] размеров [math](ntimes1)[/math].
Аксиома 3 называется неравенством треугольника.
Примером нормы матрицы-столбца может быть семейство норм
[math]|x|= Biggl(sum_{i=1}^{n}|x_i|^pBiggr)^{1/p},[/math]
где при любом целом положительном [math]p[/math] определяется функция, удовлетворяющая условиям 1-3.
Приведем часто используемые нормы матриц-столбцов.
1. [math]|x|_1=max_{iinmathbb{N}}|x_i|[/math] — максимум среди модулей элементов столбца;
2. [math]textstyle{|x|_2=sumlimits_{i=1}^{n}|x_i|}[/math] — сумма модулей элементов столбца;
3. [math]textstyle{|x|_3=sqrt{sumlimits_{i=1}^{n}x_i^2}}[/math] — квадратный корень из суммы квадратов элементов.
Последняя норма называется евклидовой, так как совпадает с модулем столбца (длиной вектора), т.е. [math]|x|_3=|x|=sqrt{x^Tx}[/math].
Замечания 10.1
1. Можно показать, что справедливы следующие соотношения
[math]|x|_2geqslant|x|_3geqslant|x|_1[/math], а также [math]sqrt{n}cdot|x|_3geqslant|x|_2,~ sqrt{n}cdot|x|_1geqslant|x|_3[/math].
2. Норма может быть использована при анализе сходимости последовательностей матриц-столбцов.
Последовательность матриц-столбцов [math]bigl{x^{(1)},x^{(2)},ldots,x^{(k)},ldotsbigr}[/math] сходится к столбцу [math]x_{ast}[/math], если [math]lim_{kto+infty}x_i^{(k)}=x_{ast i}[/math], для всех [math]i=1,2,ldots,n[/math]. Для того чтобы последовательность [math]bigl{x^{(1)},x^{(2)}, ldots,x^{(k)},ldotsbigr}[/math] сходилась к столбцу х., необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|x^{(k)}-x_{ast}bigr|=0[/math].
3. Для определения псевдорешений систем линейных алгебраических уравнений ранее использовалась евклидова норма [math]|x|_3[/math].
4. Нормы позволяют оценить скорость сходимости последовательностей. Рассмотрим последовательность [math]bigl{x^{(k)}bigr}[/math], сходящуюся к [math]x_{ast}[/math]. Предположим, что все ее элементы различны и ни один из них не совпадает с [math]x_{ast}[/math]. Наиболее эффективный способ оценивания скорости сходимости состоит в сопоставлении расстояния [math]bigl|x^{(k+1)}-x_{ast}bigr|[/math] между [math]x^{(k+1)}[/math] и [math]x_{ast}[/math] с расстоянием [math]bigl|x^{(k)}-x_{ast}bigr|[/math] между [math]x^{(k)}[/math] и [math]x_{ast}[/math].
Последовательность [math]bigl{x^{(k)}bigr}[/math] называется сходящейся с порядком [math]{p}[/math], если [math]{p}[/math] — максимальное число, для которого
[math]0leqslant lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p} < +infty.[/math]
Поскольку величина [math]{p}[/math] определяется предельными свойствами [math]bigl{x^{(k)}bigr}[/math], она называется асимптотической скоростью сходимости.
Если последовательность [math]bigl{x^{(k)}bigr}[/math] — сходящаяся с порядком [math]{p}[/math], то число
[math]c=lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p},.[/math]
называется асимптотическим параметром ошибки. Если [math]p=1,~ c<1[/math], то сходимость линейная, если [math]p=2[/math] — квадратичная, если [math]p=3[/math] — кубическая и т.д. Если [math]p>1[/math] или [math]p=1,~c=0[/math], то сходимость сверхлинейная. Линейная сходимость является синонимом сходимости со скоростью геометрической профессии. Сверхлинейная сходимость является более быстрой, чем определяемая любой геометрической прогрессией.
Пример 10.1. Вычислить нормы матрицы-столбца [math]x=begin{pmatrix} 1&-2&3&-4 end{pmatrix}^T[/math].
Решение.
[math]begin{aligned} mathsf{1)}~, |x|_1&= max_{iinmathbb{N}}|x_i|= maxbigl{|1|,|-2|,|3|,|-4|bigr}=4,;\[5pt] mathsf{2)}~, |x|_2&= sum_{i=1}^{4}|x_i|= |1|+|-2|+|3|+|-4|=10,;\[5pt] mathsf{3)}~, |x|_3&= sqrt{sum_{i=1}^{4}x_i^2}= sqrt{1^2+(-2)^2+3^2+(-4)^2}=sqrt{30},. end{aligned}[/math]
Заметим, что свойство [math]|x|_2geqslant|x|_3geqslant|x|_1[/math], очевидно, выполняется.
Пусть [math]A[/math] — произвольная матрица размеров [math](mtimes n)[/math].
Нормой матрицы [math]A[/math] называется функция [math]|A|[/math], удовлетворяющая следующим аксиомам:
1) [math]|A|geqslant0[/math] для любой матрицы [math]A[/math], причем [math]|A|=0[/math] в том и только в том случае, если [math]A[/math] — нулевая матрица;
2) [math]|alphacdot A|=|alpha|cdot|A|[/math] для любого действительного числа [math]alpha[/math];
3) [math]|A+B|leqslant|A|+|B|[/math] для любых двух матриц [math]A[/math] и [math]B[/math] размеров [math](mtimes n)[/math] (неравенство треугольника);
4) [math]|Acdot B|leqslant|A|cdot|B|[/math] для любых двух матриц, у которых определено произведение.
Матричные нормы удобно определять через нормы матриц-столбцов. Для этого, задавшись какой-нибудь нормой для матриц-столбцов, рассматриваются значения [math]|Ax|[/math] при всевозможных х, удовлетворяющих условию [math]|x|=1[/math]. Максимальное из этих значений, которое найдется всегда, берется в качестве нормы матрицы [math]Acolon, |A|= max_{|x|=1}|Ax|[/math]. Такую матричную норму называют индуцированной.
Заметим, что в качестве определения индуцированной матричной нормы часто используется выражение [math]|A|=sup_{xne0}frac{|Ax|}{|x|}[/math], характеризующее максимальную величину, на которую преобразование, описываемое матрицей [math]A[/math], может растянуть любой ненулевой вектор в заданной норме.
Наиболее употребительными являются следующие формулы для вычисления значений норм матриц с действительными элементами.
1) [math]textstyle{|A|_1= maxlimits_{1leqslant ileqslant m}sumlimits_{j=1}^{n}|a_{ij}|}[/math] — максимум суммы модулей элементов в строке;
2) [math]textstyle{|A|_2= maxlimits_{1leqslant jleqslant n}sumlimits_{i=1}^{m}|a_{ij}|}[/math] максимум суммы модулей элементов в столбце;
3) [math]|A|_3=sqrt{lambda_{max}(A^TA)}[/math] — квадратный корень из максимального собственного значения [math]lambda_i[/math] матрицы [math]A^TA[/math];
4) [math]textstyle{|A|_4= sqrt{sumlimits_{i=1}^{m} sumlimits_{j=1}^{n} a_{ij}^2}}[/math] — квадратный корень из суммы квадратов элементов.
Заметим, что вычисление нормы [math]|A|_3= sqrt{lambda_{max}(A^TA)}[/math] связано с весьма трудоемкими операциями. Поскольку справедливо неравенство
[math]|A|_3=sqrt{lambda_{max}(A^TA)} leqslant |A|_4= sqrt{sumlimits_{i=1}^{m} sum_{j=1}^{n} a_{ij}^2},[/math]
то норма [math]|A|_4[/math] часто используется в оценках вместо [math]|A|_3[/math]. Норма [math]|A|_4[/math] возникает, если матрице [math]A[/math] поставить в соответствие “длинный столбец”:
[math]begin{pmatrix}a_{11},a_{21},ldots, a_{m1},a_{12},a_{22},ldots, a_{m2},ldots,a_{nn} end{pmatrix}^T[/math] и применить норму [math]|x|_3[/math].
Пример 10.2. Вычислить нормы матриц [math]A=begin{pmatrix}1&-2&3\ 4&5&-6\ -7&8&9 end{pmatrix}!,~ B=begin{pmatrix}1&0&0\ 0&1&0\ 0&0&1 end{pmatrix}[/math].
Решение. а)
[math]begin{aligned}|A|_1&= maxbigl{|1|+|-2|+|3|;, |4|+|5|+|-6|;, |-7|+|8|+|9|bigr}= max{6;,15;,24}=24;\[5pt] |A|_2&= maxbigl{|1|+|4|+|-7|;, |-2|+|5|+|8|;, |3|+|-6|+|9|bigr}= max{12;15;18}=18;\[5pt] |A|_4&= sqrt{1^2+(-2)^2+3^2+4^2+5^2+(-6)^2+(-7)^2+8^2+9^2}=\[2pt] &=sqrt{1+4+9+16+25+36+49+64+81}= sqrt{285};end{aligned}[/math]
б) [math]|B|_1=|B|_2=1,,~ |B|_4=sqrt{1+1+1}=sqrt{3}[/math].
Норма матриц может быть использована при анализе сходимости различных численных процедур. Пусть имеется последовательность матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] размеров [math]mtimes n[/math]. Матрица [math]A[/math] называется пределом последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math], если [math]lim_{kto+infty}a_{ij}^{(k)}=a_{ij}[/math] для всех [math]i=1,ldots,m[/math] и [math]j=1,ldots,n[/math]. Это обозначается [math]lim_{kto+infty}A^{(k)}=A[/math].
Для сходимости последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] к матрице [math]A[/math] необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|A^{(k)}-Abigr|=0[/math]. При этом последовательность, составленная из норм матриц [math]A^{(k)}[/math], сходится к норме матрицы [math]A[/math], т.е. [math]lim_{kto+infty} bigl|A^{(k)}bigr|=|A|[/math].
Отметим некоторые свойства предела матриц. Если [math]lim_{kto +infty}A^{(k)}=A,~ lim_{kto+infty}B^{(k)}=B[/math], то:
[math]begin{array}{ll}mathsf{1)}~ limlimits_{kto+infty}bigl[A^{(k)}pm B^{(k)}bigr]=Apm B;&qquad mathsf{2)}~ limlimits_{kto+infty}bigl[A^{(k)}cdot B^{(k)}bigr]=Acdot B;\\[-5pt] mathsf{3)}~ limlimits_{kto+infty}bigl[A^{(k)}bigr]^{-1}=A^{-1};&qquad mathsf{4)}~ limlimits_{kto+infty}bigl[CA^{(k)}bigr]=CA,~ limlimits_{kto+infty}bigl[A^{(k)}Dbigr]=AD.end{array}[/math]
где считается, что все операции определены.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Вычисление нормы и чисел обусловленности матрицы
1
норма матрицы представляет из себя
максимальное из чисел, полученных при
сложении всех элементов каждого столбца,
взятых по модулю. Не путайте со сложением
матриц!
Р
ассмотрим
на примере: пусть дана матрица размера
3х2. В первом столбце стоят элементы: 8,
3, 8. Все элементы положительные. Найдем
их сумму: 8+3+8=19. В втором столбце стоят
элементы: 8, -2, -8. Два элемента – отрицательные,
поэтому при сложении этих чисел,
необходимо подставлять модуль этих
чисел (т.е. без знаков “минус”).
Найдем их сумму: 8+2+8=18. Максимальное из
этих двух чисел – это 19. Значит первая
норма матрицы равна 19.
2
норма матрицы представляет из себя
квадратный корень из суммы квадратов
всех элементов матрицы. А это значит мы
возводим в квадрат все элементы матрицы,
затем складываем полученные значения
и из результата извлекаем квадратный
корень.
В
нашем случае, 2 норма матрицы получилась
равна квадратному корню из 269. На схеме,
я приближенно извлекла квадратный
корень из 269 и в результате получила
приблизительно около 16,401. Хотя более
правильно не извлекать корень.
3
норма матрицы представляет из себя
максимальное из чисел, полученных при
сложении всех элементов каждой строки,
взятых по модулю.
В
нашем примере: в первой строке стоят
элементы: 8, 8. Все элементы положительные.
Найдем их сумму: 8+8=16. В второй строке
стоят элементы: 3, -2. Один из элементов
отрицательный, поэтому при сложении
этих чисел, необходимо подставлять
модуль этого числа. Найдем их сумму:
3+2=5. В третьей строке стоят элементы 8,
и -8. Один из элементов отрицательный,
поэтому при сложении этих чисел,
необходимо подставлять модуль этого
числа. Найдем их сумму: 8+8=16. Максимальное
из этих трех чисел – это 16. Значит третья
норма матрицы равна 16.
Число
обусловленности квадратной матрицы A
определяется, как
k(A)
= ||A||·||A -1||
Число
обусловленности имеет следующее
значение: если машинная точность, с
которой совершаются все операции с
вещественными числами, равна ε, то при
решении системы линейных уравнений Ax
= b результат будет получен с относительной
погрешностью порядка ε·k(A). Хотя число
обусловленности матрицы зависит от
выбора нормы, если матрица хорошо
обусловлена, то её число обусловленности
будет мало при любом выборе нормы, а
если она плохо обусловлена, то её число
обусловленности будет велико при любом
выборе нормы. Таким образом, обычно
норму выбирают исходя из соображений
удобства. На практике наиболее широко
используют 1-норму, 2-норму и ∞-норму,
задающиеся формулами:
В
Matlab
используется следующие функции поиска
нормы:
Пусть
А —матрица. Тогда n=norm(A) эквивалентно
п=погп(А,2) и возвращает вторую норму, т.
е. самое большое сингулярное число А.
Функция n=norm(A, 1) возвращает первую норму,
т. е. самую большую из сумм абсолютных
значений элементов матрицы по столбцам.
Норма неопределенности n=norm(A, inf) возвращает
самую большую из сумм абсолютных значений
элементов матрицы по рядам. Норма
Фробениуса
(Frobenius) norm(A, ‘fro’) = sqrt(sum(diag(A’A))).
Пример:
»
A=[2,3,1;1,9,4;2,6,7]
A
=
2
3 1
1
9 4
2
6 7
»
norm(A,1)
ans
=
18
Числа
обусловленности матрицы определяют
чувствительность решения системы
линейных уравнений к погрешностям
исходных данных. Следующие функции
позволяют найти числа обусловленности
матриц.
cond(X)
— возвращает число обусловленности,
основанное на второй норме, то есть
отношение самого большого сингулярного
числа X к самому малому. Значение cond(X),
близкое к 1, указывает на хорошо
обусловленную матрицу;
с
= cond(X,p) — возвращает число обусловленности
матрицы, основанное на р-норме:
norm(X,p)*norm(inv(X),p), где р определяет способ
расчета:
р=1
— число обусловленности матрицы,
основанное на первой норме;
р=2
— число обусловленности матрицы,
основанное на второй норме;
p=
‘fro’ — число обусловленности матрицы,
основанное на норме Фробе-ниуса
(Frobenius);
р=’inf’
— число обусловленности матрицы,
основанное на норме неопределенности.
с
= cond(X) — возвращает число обусловленности
матрицы, основанное на второй норме.
Пример:
»
d=cond(hilb(4))
d
=
1.5514е+004
condeig(A)
— возвращает вектор чисел обусловленности
для собственных значений А. Эти числа
обусловленности — обратные величины
косинусов углов между левыми и правыми
собственными векторами;
[V.D.s]
= condeig(A) — эквивалентно
[V,D] = eig(A): s = condeig(A);.
Большие
числа обусловленности означают, что
матрица А близка к матрице с кратными
собственными значениями.
Пример:
»
d=condeig(rand(4))
d
=
1.0766
1.2298
1.5862
1.7540
rcond(A)
— возвращает обратную величину
обусловленности матрицы А по первой
норме, используя оценивающий обусловленность
метод LAPACK. Если А — хорошо обусловленная
матрица, то rcond(A) около 1.00, если плохо
обусловленная, то около 0.00. По сравнению
с cond функция rcond реализует более
эффективный в плане затрат машинного
времени, но менее достоверный метод
оценки обусловленности матрицы.
Пример:
»
s=rcond(hilb(4))
s
=
4.6461е-005
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень, умножить матрицу на число, сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы 
Кнопка 



Рис.1
При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки 
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы 
Рис.2
Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку “A+B “,”A-B” или “A×B”.
Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки
.
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку “обратное “.
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу
или
с помощью радиокнопки
.
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку “определитель “.
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу
или
с помощью радиокнопки
.
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку “ранг “.
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки
.
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку “псевдообратное “.
Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу
или
с помощью радиокнопки
.
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку “полный ранг строк ” или “полный ранг столбцов”.
Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу
или
с помощью радиокнопки
.
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку “скелетное разложение “.
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку “решение AX=B”.
Учтите, что матрицы 
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу
или
с помощью радиокнопки
.
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку “Треугольный вид”.
LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
Для LU(LUP)-разложения:
- Выберите матрицу
или
с помощью радиокнопки
.
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку “LU-разложение”.
Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу
или
с помощью радиокнопки
.
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку “ядро (·)”.
Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.
Для ортогонализации или ортонормализации матрицы:
- Выберите матрицу
или
с помощью радиокнопки
.
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку “Ортогонализация Г.-Ш. (·)” или “Ортонормализация Г.-Ш. (·)”.


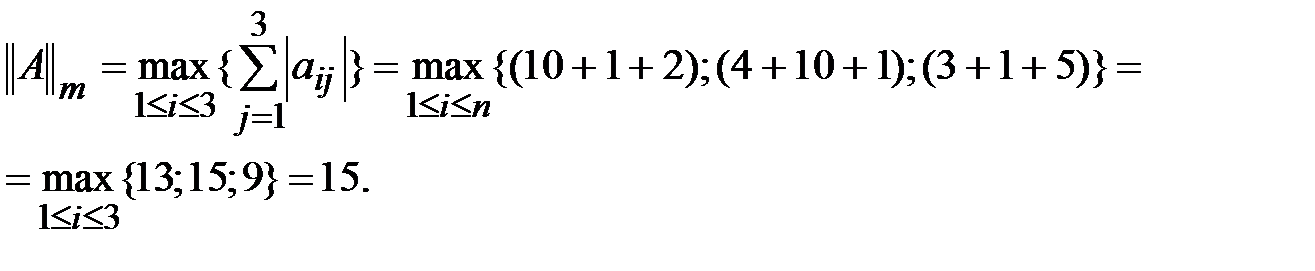
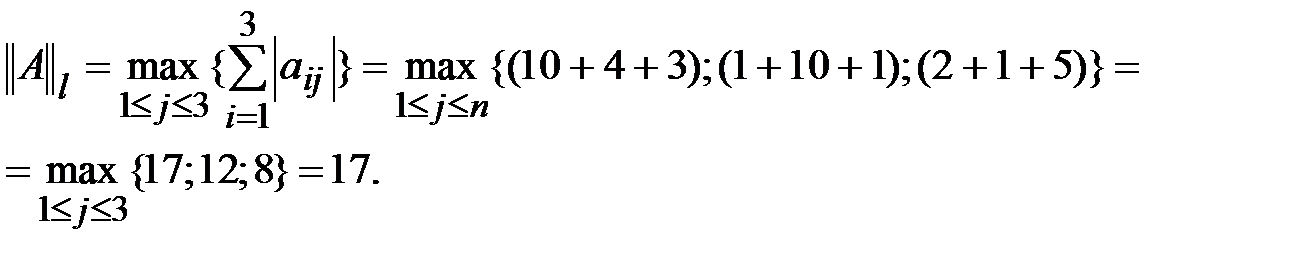

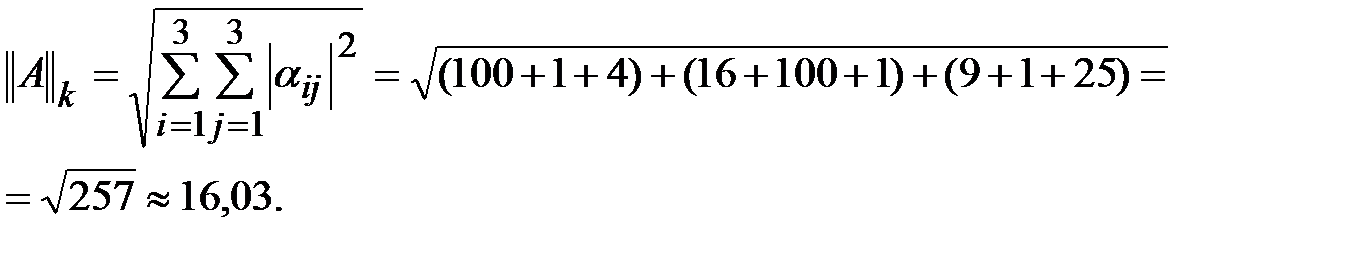
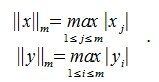
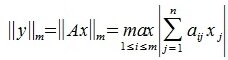
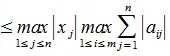
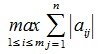
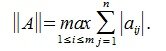
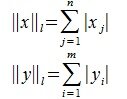
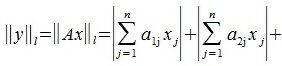
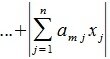
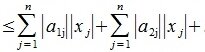
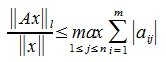
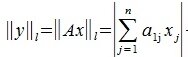
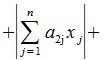
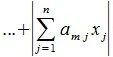
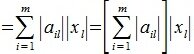
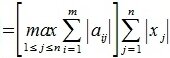
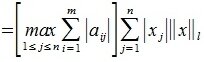
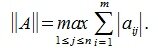
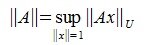
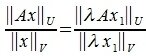
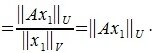
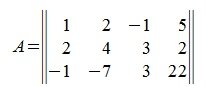
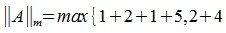
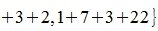
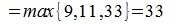
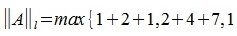
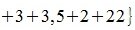
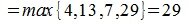
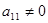 . Первую строку оставляем без изменений.
. Первую строку оставляем без изменений.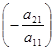 .
.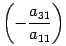 .
.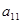 .
.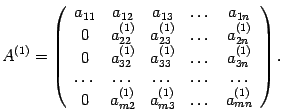
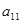 . В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что
. В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что 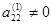 .
.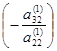 . В результате получим, что второй элемент третьей строки равен нулю.
. В результате получим, что второй элемент третьей строки равен нулю.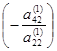 , и т.д. В результате получаем матрицу
, и т.д. В результате получаем матрицу







