
Привет всем читателям Блога Вебинвестора! Думаю, каждый из вас сталкивался с начислением процентов на денежную сумму — по депозиту, по кредиту, расчётом доходности инвестиций и так далее. Так вот, если повторить эту процедуру много раз, вложения начинают расти всё быстрее и быстрее благодаря эффекту сложного процента! Воистину, это один из главных секретов, как с помощью инвестирования увеличить количество нулей в сумме на вашем банковском счёте.
Эта статья входит в бесплатное обучение инвестициям с нуля на Блоге Вебинвестора. В комментариях к статье вы можете оставлять любые вопросы по теме и я постараюсь подробно на них ответить.
Приглашаю подписываться на мой Telegram-канал Блог Вебинвестора! Там вы найдёте еженедельные отчёты по инвестициям, аналитические материалы, комментарии по важным новостям и многое другое. Также прошу делиться ссылкой на блог в социальных сетях и мессенджерах:
Что такое простой и сложный процент
и чем они отличаются
Понятие простых и сложных процентов — один из самых важных уроков по финансовой грамотности, которые вы должны знать. Они встречаются в нашей жизни повсюду: от ежедневных покупок (кэшбек, бонусы) до инвестирования (проценты на депозит, дивиденды, комиссии и т.д.) и оказывают незаметное, но существенное влияние на ваш кошелек на длинной дистанции. Чтобы наглядно увидеть различия между простыми и сложными процентами, давайте рассмотрим примеры.
Простой процент — прибыль в % начисляется только на первоначальную сумму вклада и сразу выводится.
Допустим, вы открыли депозит 10000$ под 10% годовых, проценты начисляются раз в год. По схеме простого процента каждые 12 месяцев вы будете получать 1000$ прибыли, но она не остаётся на депозите и сразу же выводится. В итоге прирост прибыли будет выглядеть так:

Всё «просто» — каждый год плюс тысяча в карман. Простой процент используется в случаях, когда база начисления процентов не изменяется. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты начисляются на первоначальную сумму вклада плюс всю полученную до этого прибыль. Понятия «реинвестирование» и «капитализация» по сути означают использование сложного процента.
Для сравнения пусть будет тот же депозит 10000$ под 10%, но банк в этот раз разрешает оставить прибыль на счёте. Вот что произойдёт с вкладом за 10 лет:

В первый год разницы нет — всё та же тысяча, но поскольку сумма на депозите теперь растёт, уже на втором году прибыль увеличивается: 2100$ вместо 2000$, за третий год 3310$ вместо 3000$ и так далее. За 10 лет доходность нашего депозита составила 159% вместо 100% когда мы выводили прибыль. Неплохая прибавка, не так ли? А вот что случится еще через несколько десятилетий:

Впечатляет! Чем дольше открыт депозит, тем сильнее работает эффект сложного процента — за 50 лет можно увеличить депозит не в 6, а более чем в 100 раз. Вот как это выглядит на графике:

без капитализации депозит растёт линейно,
а с капитализацией — по экспоненте
Теперь киношные истории про забытые банковские счета, на которых накопились миллионы долларов выглядят вполне реальными 🙂 Конечно, 50 лет это много, но правило сложного процента неплохо работает и на более коротких промежутках времени — всё зависит от доходности вклада. Если хочется заработать больше, стоит использовать более прибыльные способы инвестирования: акции, драгоценные металлы, криптовалюты, валютный рынок и так далее.
Думаю, суть понятна, теперь давайте пройдемся по математической стороне вопроса, а потом рассмотрим несколько типичных примеров задач.
⬆️ К СОДЕРЖАНИЮ ⬆️
Формулы простых и сложных процентов
Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:
- К0 — начальная сумма вклада;
- К — конечная сумма вклада;
- R — ставка доходности, переводится из процентов в число (10% = 0.1);
- N — количество периодов (лет).
Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита. Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N).
Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.
⬆️ К СОДЕРЖАНИЮ ⬆️
Примеры решения задач
по сложным процентам
В этом разделе мы пройдемся по некоторым типичным задачам на сложные проценты. Также вы найдете шаблоны расчётов в Excel, в которых можно поменять вводные данные и получить нужное вам решение.
Задача №1. Рассчитать прибыль по вкладу на 5 лет под 10% годовых, начальная сумма вложений 100000 рублей (с капитализацией).
Находим конечную сумму вклада по формуле сложных процентов:
Вычисляем прибыль:
Результат: инвестор через 5 лет получит 61051 рублей прибыли.
Задача №2. Рассчитать прибыль по вкладу на 10 лет под 10% годовых с капитализацией. Начальная сумма вложений 50000 рублей, дополнительно каждый год начиная с первого счёт пополняется на 10000 рублей.
Сначала находим конечную сумму по формуле сложного процента с регулярными пополнениями:

Учитывая, сколько инвестировано за 10 лет (50000 сразу и еще 9 раз по 10000), вычисляем прибыль:
Результат: инвестор через 10 лет получит 139061 рубль прибыли, инвестировав 140000 рублей.
Задача №3. Рассчитать, сколько времени понадобится инвестору, чтобы увеличить капитал с 500000 до 1000000 рублей. Средняя доходность портфеля — 12% годовых, прибыль реинвестируется.
У нас есть все необходимые данные, используем одну из производных формул сложных процентов:

Решение: инвестору понадобится чуть больше 6 лет.
Задача №4. Посчитать среднюю процентную ставку, которая позволит превратить 100000 рублей в 500000 рублей за 10 лет путём инвестирования. Прибыль реинвестируется.
Используем одну из производных формул сложных процентов:

Решение: инвестору нужно вложить деньги под 17.5% годовых (довольно сложно на практике, кстати).
Думаю, этого достаточно. Если ваша задача не похожа ни на одну из предыдущих, возможно вам поможет информация из следующего раздела статьи.
⬆️ К СОДЕРЖАНИЮ ⬆️
Калькулятор сложных процентов в Excel
Конечно же, задачи на сложные проценты целесообразнее решать в MS Excel по уже известным вам из предыдущих разделов формулам. По ходу статьи вы уже могли скачать некоторые примеры типичных задач, но если этого мало — предлагаю полную подборку калькуляторов по сложным процентам, реализованную в одном Excel-файле. Получить его можно бесплатно, просто заполните форму ниже:
Если письмо не пришло, проверяйте папку «Спам», иногда попадает туда. Если не видите форму подписки, оставьте комментарий к статье и я добавлю ваш электронный адрес вручную.
Вот какие задачи по простым и сложным процентам может решать «Коллекция калькуляторов для инвестора»:
- расчёт конечной суммы вклада;
- расчёт начальной суммы вклада;
- расчёт необходимой процентной ставки;
- расчёт срока инвестирования;
- расчёт конечной суммы вклада с учётом регулярных пополнений и капитализацией;
- ожидаемый пассивный доход в каждом из случаев.
В будущем я планирую добавить много калькуляторов по самым разным темам, оставляйте свои пожелания в комментариях!
Пример одного из калькуляторов для расчёта сложных процентов в Excel:

Дополнительно к каждому калькулятору автоматически строится график доходности вклада с капитализацией и без:

А также уже знакомые вам таблицы:

Думаю, файл будет полезен и для практического использования, и в обучающих целях — в готовом виде есть все формулы, по которым можно считать сложные проценты в Excel.
⬆️ К СОДЕРЖАНИЮ ⬆️
Как использовать сложные проценты
в инвестировании
Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.
Статья в тему: Как деньги делают еще больше денег или Что такое реинвестирование
Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты. Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:

Источники: statbureau.org
Даже если оставить удачный бескризисный отрезок 2010-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2014 года, очевидно, находится в еще большем минусе.
Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.
Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:

Источник: ru.investing.com
Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция. По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы.
Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:
- Акции, в особенности американские. Сейчас это один из немногих активов, которые растут большую часть времени. Кроме того, многие компании платят дивиденды, которые можно реинвестировать и еще сильнее разгонять сложный процент. Плюс, рост цен на сами акции способен перекрыть влияние инфляции, а комиссии зависят от объема торгов, а не от вашего вклада. Взгляните на самых богатых людей планеты — почти все сделали состояние, владея большим количеством акций в своих компаниях.
- Инвестиционные фонды (в т.ч. ETF). Чаще всего это тоже инвестиции в акции, но вам не нужно самостоятельно подбирать портфель — аналитики фонда все сделают за вас. Если в портфеле фонда есть дивидендные акции, вы опять же сможете реинвестировать выплаты. При комиссии за участие ниже 1% в год катастрофического влияния на доходность ваших инвестиций не будет.
- Облигации. Обычно они дают чуть большую доходность, чем банковский депозит и способны практически без рисков приносить небольшую прибыль с учётом инфляции. В любом случае в вашем инвестиционном портфеле должны быть надёжные долгосрочные вложения, и облигации для этих целей подходят неплохо. Расходы при вложении в облигации идут на услуги фондового брокера и не зависят от общей суммы инвестиций.
Оптимальный портфель инвестора предполагает использование всех этих инструментов, поскольку генерируемый ими денежный поток позволяет гибко управлять вложениями: делать ребалансировку, выводить прибыль или реинвестировать. Использовать правило сложных процентов можно в любых инвестициях, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.
⬆️ К СОДЕРЖАНИЮ ⬆️
Использование сложных процентов — теоретически очень выгодное занятие, но как всегда дьявол кроется в деталях. Тем не менее, реинвестирование/капитализация остаётся одним из главных инструментов для накопления большого капитала, грех его игнорировать. И даже вне инвестирования начисление процентов по простому или сложному принципу встречается часто, поэтому полезно знать как это все работает. Надеюсь, подробный разбор формул и решения задач будут вам полезны.
Удачных инвестиций и не болейте!

Г.А. МЕДВЕДЕВ
НАЧАЛЬНЫЙ КУРС
ФИНАНСОВОЙ МАТЕМАТИКИ
Москва ТОО «Остожье»
2000
УДК 51:336(075.3)
ББК 22.1я721+65.9(2)26я721 М42
ПРИ УЧАСТИИ ООО «НОВОЕ ЗНАНИЕ»
Рекомендовано к изданию Советом факультета прикладной математики и информатики
и
Советом специального факультета бизнеса и информационных технологий Белорусского государственного университета
Медведев Г.А.
М42 Начальный курс финансовой математики: Учеб.пособие.-М.: ТОО
«Остожье»,2000. – 267с.
|
ISBN 5-86095-117-5 |
|
|
В пособии излагаются основные методы |
финансовых расчетов, |
составляющих предмет финансовой математики. Для понимания этих методов достаточно иметь знания в объеме математики старших классов средней школы. Изложение материала в книге снабжено большим количеством примеров, которых достаточно для понимания этого материала и для иллюстрации расчетов. В книге приводятся упражнения по всем рассматриваемым разделам, что позволяет использовать ее в качестве учебного пособия для факультативного изучения финансовой математики в школах (лицеях или гимназиях), а также на первых курсах вузов на специальностях с экономическим или финансовым уклоном, например таких как «Актуарная математика», «Финансы и кредит», «Экономическая кибернетика» и др. Кроме того, книга может служить
|
учебным пособием по дисциплине |
специализации «Основы математики |
|
финансов» в тех вузах, где такая дисциплина предусмотрена. |
|
|
УДК 51:336(075.3) |
|
|
ББК 22.1я721+65.9(2)26я721 |
|
|
©Г.А.МЕДВЕДЕВ |
|
|
ISBN 5-86095-117-5 |
© ОФОРМЛЕНИЕ. ИЗДАТЕЛЬСТВО |
|
«НОВОЕ ЗНАНИЕ»,2000 |
ПРЕДИСЛОВИЕ
В настоящее время интерес к финансовой деятельности заметно вырос, однако культура финансовых расчетов еще невысока. Особенно это касается случаев, когда такие расчеты делаются при анализе платежей, которые разнесены во времени или составляют потоки (последовательности, серии) регулярно повторяющихся выплат. До последнего времени нашим обществом практически совершенно не использовались ценные бумаги, векселя и другие финансовые атрибуты; имеется слабое представление об определении их рыночной цены. Пока еще основная масса людей недостаточно информирована о разнообразных формах получения и использования процентных денег.
Представляется целесообразным ознакомить широкого читателя с основами финансовых расчетов, составляющих предмет финансовой математики. Для понимания этих основ достаточно иметь знания в объеме
|
математики старших |
классов |
средней школы. |
Поэтому предлагаемая |
|
|
читателю |
книга в |
первую очередь адресована старшим школьникам и |
||
|
студентам |
первых |
курсов |
и предназначена |
для ознакомления с |
математическими основами финансов, их применением для расчетов, считающихся обычными в странах с развитой финансовой культурой. Не секрет, что пока многие работники финансовых учреждений также недостаточно осведомлены об этом. Для них эта книга также будет полезной. Кроме того, каждому человеку, имеющему свободные деньги, следует уметь ими распорядиться с целью их приумножения. Эта книга научит их делать необходимые расчеты для достижения этой цели и производить правильный выбор, если имеются различные варианты.
Изложение материала в книге сделано по уже сложившемуся классическому стандарту. Дается понятие о процентных деньгах; простых и сложных процентах; дисконтировании (учете изменения стоимости денег со временем из-за возможности получения процентов); эквивалентности платежей; аннуитетов (серий регулярных платежей) и вечных рент. Эти понятия используются для описания элементов практической финансовой деятельности, таких как оформление векселей и их купля/продажа; амортизация (постоянная выплата) долгов; купля/продажа в рассрочку; образование целевых денежных фондов; расчет инвестиций; оперирование с простейшими ценными бумагами-облигациями; определение их рыночной цены; амортизация и обесценивание оборудования.
3
В настоящее время литературы на русском языке по финансовой математике практически нет. Автору известно лишь руководство Е.М. Четыркина «Методы финансовых и коммерческих расчетов», Москва, Дело Лтд. 1995. Поэтому при написании этой книги автору пришлось использовать иностранные источники. Он опирался, в основном, на следующие учебники (перечислим их по возрастанию сложности) :
1.R. Cissell, H. Cissell, D. Flaspohler. Mathematics of Finance. Houghton Mifflin Company, Boston, 1990 (восьмое издание), 720 с.
2.P.Hummel, C. Seebeck. Mathematics of Finance. McGraw-Hill Inc., New York, 1980 (третье издание), 370 с.
3.S. Kellison. The Theory of Interest. Irwin Inc., Boston, 1991 (второе издание), 446 с.
4.H. Gerber. Life Insurance Mathematics. Springer-Ferlag, Berlin, 1996 (второе издание), 157 с.
5.J. McCutcheon, W. Scott. An Introduction to the Mathematics of Finance.
Butterworth-Heinemann, Oxford, 1996 (восьмое издание), 463 с.
Предлагаемая читателю книга по уровню сложности занимает место между первым и вторым из этих учебников.
Традицией финансовых работников является использование «Таблиц для финансовых расчетов». Вместе с тем появление и широкое распространение вычислительной техники в большой степени понизило роль этих таблиц, так как возможности компьютерного применения значительно шире, а получение результатов быстрее и удобнее. Поэтому при изложении уделяется некоторое внимание употреблению таблиц. К сожалению из-за ограниченности объема сами таблицы в книге не приводится, но в приложении приведено описание этих таблиц, а также приведены формулы, по которым они составляются. Так что каждый читатель, которому доступны даже простейшие вычислительные средства (от программируемых калькуляторов и выше) может сосчитать необходимые значения функций по приведенным формулам. Читатели, которым доступно использование персональных компьютеров, могут воспользоваться дискетой с компьютерной программой, которая специально подготовлена для работы с этой книгой и обеспечивает расчеты в более широком диапазоне, чем это позволяют сделать «Таблицы для финансовых расчетов».
Профессор Медведев Г.А. Белорусский государственный университет
220050 г. Минск, пр. Ф. Скорины 4. Тел. (017) 2095448.
4
Глава 1. ПРОЦЕНТНЫЕ ДЕНЬГИ
1.1 ПРОЦЕНТЫ
Всякий собственник, имеющий квартиру или гараж, которые он не использует, может сдать их в наем, получая за это определенную плату. Точно также человек, имеющий деньги, которые он не использует, может их дать взаймы другому лицу (или, используя более общий термин, – инвестировать) за определенное вознаграждение. Доход от инвестированного капитала или, в более узком смысле, вознаграждение за использование денег, называется процентными деньгами или кратко процентами. Сумма денег, данных взаймы, называется основной или капиталом. Обычно заем дается на определенное время – период. Сумма процентных и основных денег, полагающаяся в конце периода, называется итогом. В общем случае отношение процента за период к основной сумме (капиталу) называется нормой процента. Эта норма чаще всего выражается в форме процентов, при расчетах используются эквивалентные десятичные (реже – натуральные) дроби. При заключении конкретных сделок для обозначения нормы процентов обычно используется другое название – процентная ставка.
ПРИМЕР Иванов взял в сберегательном банке ссуду 10000 рб. Если банк начисляет 250 рб процентных денег за использование этой суммы в течение 6 месяцев, какой будет норма процента за этот период ?
РЕШЕНИЕ Обозначим норму процента за шести месячный период через i. Тогда i = 250/10000 = 0.025 = 2.5%.
1.2 ПРОСТОЙ ПРОЦЕНТ
Пусть P будет основной суммой. r – нормой процента за 1год и t – продолжительность периода времени в годах. Если процент вычисляется по формуле
и если процент выплачивается в конце периода времени, тогда выплачиваемые процентные деньги называются простым процентом. В этом случае норма процента за рассматриваемый период времени равна rt. Для простого процента норма, как правило, дается для периода продолжительностью 1 год.
5
Если S обозначает итоговую сумму, тогда
Равенства (1) и (2) называются основными уравнениями простого процента. Любая задача для простых процентов может быть решена при помощи этих двух равенств. Следует заметить, что они содержат пять различных переменных, а именно S, P, I, r и t. Если любые три заданы (исключая случай задания трех первых одновременно), остальные две могут быть найдены с помощью (1) и (2). Для удобства можно добавить еще одно равенство. Если исключить из (1) и (2) переменную I, получим выражение итоговой суммы S через P, r и t.
|
S = P(1 + rt) |
(3) |
||||
|
Так как для простого процента r |
всегда дается как |
годовая норма, время |
|||
|
t должно измеряться в годах. |
Когда |
время дается в месяцах, t равно |
|||
|
числу |
месяцев, |
поделенному |
на 12. Когда время дается в днях, |
||
|
используется два |
различных способа для подсчета |
t. Чаще используется |
|||
|
деление |
числа |
дней на 360. |
Если |
t вычисляется таким способом, |
полученный процент называется обыкновенным простым процентом.
Второй способ – использовать деление числа дней на 365 (366 в високосном году). Если t вычисляется таким образом, полученный процент называется точным простым процентом.
ПРИМЕР 1 Найти простой процент за ссуду 3000 рб на 5 месяцев при норме 0,07%.
РЕШЕНИЕ Мы имеем P = 3000, r = 0,07 и t = 5/12.
I = Prt = 3000 × 0,07 × (5/12) = 87,5 рб.
ПРИМЕР 2 Найти точный простой процент и итоговую сумму, если 5000 рб даны взаймы на 100 дней при норме 4%.
РЕШЕНИЕ P = 5000, r = 0,04 и t = 100/365
I = 5000 × 0,04 × (100/365) = 54,8 рб
S = 5000 + 54,8 = 5054,8 рб.
6
ПРИМЕР 3 Человеку, который инвестировал 100000 рб, возмещены 101000 рб девяносто днями позже. С какой нормой зарабатывались эти деньги при обыкновенном простом проценте ?
|
РЕШЕНИЕ P = 100000, S = 101000 и t = 90/360 |
= 1/4. Теперь, так как |
|
S = P + I , I = S – P = 101000 – 100000 = 1000. Но |
I = Prt , поэтому |
r = I/(Pt) = 1000/(100000 × (1/4)) = 0,04 = 4%.
ПРИМЕР 4 Через 60 дней после займа Иванов выплатил ровно 10000 рб. Сколько было занято, если 10000 рб включают основную сумму и обыкновенный простой процент при 12% ?
РЕШЕНИЕ S = 10000, r = 0,12 и t = 60/360 = 1/6. Подставляя эти значения в S = P(1 + rt) , получим
10000 = P × (1,02) откуда P = 10000/ 1,02 = 9804 рб.
Для вычисления простых процентов без использования современной вычислительной техники применяются различные практические приемы. Наиболее известный из них – шести процентный способ, который основан на том, что на каждый рубль при норме 6% обыкновенный простой процент за 60 дней равен 0,01 рб. Теперь, приводя реальную норму к 6% и реальный период к 60 дням для определения обыкновенного простого процента достаточно перемножить эти приведенные величины и полученное произведение умножить на один процент от основной суммы. Полученный результат и будет обыкновенным простым процентом.
Кроме этого для определения простых процентов не прибегая к вычислениям, используются таблицы. В финансовой математике часто можно решать поставленную задачу несколькими методами. В этих условиях всегда следует искать наиболее простой способ, который сократит и ваш труд и риск числовых ошибок. Решение задач несколькими способами часто является желательным с целью проверки результата.
УПРАЖНЕНИЯ 1
(В этих и всех последующих упражнениях, когда результат не выражается целыми числами, вычисления производить с точностью до второго десятичного знака после запятой, если в условиях не оговорено другое.)
7
|
1. Выразить следующие |
проценты |
в |
виде |
соответствующих |
|
|
натуральных и десятичных дробей с точностью |
до |
четвертого |
|||
|
десятичного знака : a) 4 %, |
b) 2 1/4 |
%, |
c) 3&2 |
% , |
d) 3 1/3 % , |
|
e) 0,8 % , f) 1/6 % . |
2.Представить каждую из следующих дробей в виде процентов с точностью до сотой доли процента ; a) 0,035 , b) 3/40 , c) 0,04 (1/3) , d) 5/16 , e) 8,40/280 , f) 40/1250.
3.Найти значения 1 + rt и выразить результат в виде натуральных и десятичных дробей : a) r = 6%, t = 1/2; b) r = 1 1/4 %, t = 1/3; c) r = 5%,
t = 3/4; d) r = 3.2, t = 1/12; e) r = 3.2%, t = 1/8.
4.Вычислить (1 + 0,07(7/12))5000 рб с точностью до 1 рб.
5.Найти простой процент для 7000 рб за 5 месяцев при 3%.
6.Вычислить 6000рб/(1 + 0,05(1/4)) с точностью до 1 рб.
7.Найти простой процент и итоговую сумму, если 7000 рб инвестируются на 4 месяца при 6 1/3 %.
8.Найти обыкновенный и точный простой процент для 4600 рб за 120 дней при 7% в обычном году.
9.Найти обыкновенный простой процент и итоговую сумму для 150000 рб при 5 1/4 % за 90 дней.
|
10. Банк начисляет 5 рб обыкновенного простого |
процента |
за |
|
использование 300 рб в течение 60 дней. Какова |
норма простого |
|
|
процента таких сделок ? |
11.При приобретении товаров покупатель может заплатить или 500 рб сразу или 520 рб через 4 недели. Если он займет деньги, чтобы заплатить наличными, какая норма простого процента может быть допустима для возмещения займа ?
12.Найти P если S = 4800 рб, r = 7% и t = 1/4.
13.Найти S если P = 7000 рб, r = 8% и t = 1/6.
14.Какая основная сумма приведет к итогу 7800 рб за 5 месяцев, если норма процента равна 8% ?
15.Какая основная сумма приведет к итогу 13900 рб через 90 дней при норме 8% обыкновенного простого процента ?
16.Сколько дней понадобится, чтобы 7000 рб заработали 100 рб, если они инвестируются при 9% обыкновенного простого процента ?
Найти точный и обыкновенный простые проценты :
17.P = 28000, r = 7%, t = 189 дней.
18.P = 96800, r = 6%, t = 227 дней.
19.P = 69500, r = 4,5%, t = 95 дней.
20.P = 18700, r = 12%, t = 128 дней.
8
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 1
Определите,
какой из вариантов кредитования (по уровню доходности по ставке простых
процентов) наиболее выгоден для заемщика:
– сумма
первоначального долга 120000 рублей; срок кредитования 250 дней; наращенная
сумма долга 130000 рублей;
– сумма
первоначального долга 120000 рублей; срок кредитования 180 дней; наращенная
сумма долга 128000 рублей;
– сумма
первоначального долга 120000 рублей; срок кредитования 320 дней; наращенная
сумма долга 136000 рублей;
Задача 2
Клиент взял
в банке кредит на 180 дней по номинальной ставке 16% и в конце срока вернул всю
сумму долга с процентами, что составило 310 тыс. руб. Определить сумму
выданного кредита.
Задача 3
На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.
Задача 5
5 июня клиент взял кредит 200 тыс. руб. При
погашении кредита единым платежом клиент заплатил 230 тыс. руб. Определить срок
операции и дату погашения кредита, если в операции использовалась простая
процентная ставка 18% годовых (точные проценты с фактическим сроком операции).
Задача 6
Через 120
дней с момента подписания кредитного договора заемщик должен вернуть банку 750
тыс. руб. Процентная ставка по кредиту равна 18% годовых. Чему равна
первоначальная сумма долга?
Задача 7
Банк
принимает депозиты на 3 месяца по ставке 50% годовых, на 6 месяцев по ставке
70% годовых и на год по ставке 90% годовых. Определить суммы, которые может
получить владелец депозита 4500 руб., выбрать наиболее выгодный вариант
размещения вклада.
Задача 8
Банк
объявил следующие условия выдачи ссуды на один год: за первый квартал ссудный
процент 50%; за второй квартал – 75%; за третий – 100%; за четвертый квартал –
125%. Определить сумму к возврату в банк, если ссуда составляет 200000 руб.
Задача 9
Найдите
простой процент, начисленный за четыре месяца по ставке 1% на сумму 10 тыс.
руб.
Задача 10
Ссуда в
размере 50 тыс. руб. была выдана на полгода при условии начисления на нее
простых процентов по ставке 20%. Определите сумму погашения.
Задача 11
Банк
начисляет 10 тыс. руб. за использование 800 руб. в течение 60 дней. Найдите
простую процентную ставку, если применяются обыкновенные проценты.
Задача 12
Какая
сумма необходима для того, чтобы накопить за пять лет 70 тыс. руб., если на эту
сумму будут начисляться простые проценты по ставке 8%?
Задача 13
За
сколько дней сумма 800 тыс. руб. увеличится до 900 тыс. руб., если на исходную
сумму начисляются обыкновенные простые проценты по ставке 9%?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Сумма 100
тыс. руб. была получена в долг 20 января с условием начисления на нее точных
простых процентов по ставке 25% и возвращения денег через год в сумме 120 тыс.
руб. Определите дату погашения долга, если год високосный.
Задача 15
В один и
тот же день в банк были вложены сумма 20 000 руб. под 4 % годовых и сумма 18
000 руб. под 5 % годовых. Вычислите, через сколько лет оба дохода будут
одинаковыми.
Задача 16
Ставка процентов банка по вкладам до
востребования, составлявшая в начале года 10% годовых, через полгода была
снижена до 8% годовых, а еще через 3 месяца до 6% годовых. Определите общую сумму, полученную клиентом банка
через год, если им был внесен вклад в размере 10 тыс. руб.
Задача 17
Банк
предлагает разместить вкладчику 700 000 руб. на срочный депозит в трех
вариантах: а) на 1 день под 6% годовых с последующим реинвестированием
ежедневно в течение месяца; б) на 10 дней под 10% годовых с последующим
реинвестированием каждую декаду в течение месяцев; в) на 1 месяц под 18%
годовых. Определить наиболее выгодный вариант вложения денежных средств.
Задача 18
Какая сумма была внесена на счет в
банке, если по истечении 5 лет на счета стало 5200 руб. Начисление процентов
осуществлялось по схеме простых процентов по ставке 10% за каждое полугодие?
Задача 19
Ссуда в
размере 10 тыс. руб. выдается по учетной ставке простых процентов 8% годовых.
Определить срок ссуды в годах, если заемщик хочет получить 9,5 тыс. руб.
Задача 20
Проценты
по ссуде размером 5 тыс. р., выданной на два месяца, составила 125 р. Какова
процентная ставка?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 21
Кредит для покупки товара на сумму
50 тыс. руб. открыт с 12.02 до 02.10 включительно под 18% годовых. Какую сумму
заплатит должник в конце срока при начислении простых процентов? (временная база – ACT/360)
Задача 22
Найти простой процент для 7000 руб.
за пять месяцев при 3% годовых.
Задача 23
Какой капитал, будучи отдан в рост
под 7,5%, обратится через год вместе с процентными деньгами в 1343 рубля 75
копеек?
Задача 24
Ссуда
800000 руб. выдана на квартал по простой ставке процентов 20% годовых.
Определить наращенную сумму.
Задача 25
Какую сумму необходимо положить в
банк на 9 месяцев, чтобы накопить 900 руб., если он принимает вклады на
условиях 30% годовых?
Задача 26
Определите размер наращенной суммы
за один год, если первоначальная сумма равна 10 тыс. руб., первые полгода
годовая ставка простых процентов равна 18%, а вторые 21%.
Задача 27
Вклад в размере 250 000 руб.
помещен в банк по ставке 15% годовых. Спустя некоторое время получатель снял со
своего вклада 290 000 руб. Необходимо найти срок размещения вклада в
банке.
Задача 28
Через сколько лет сумма вклада
утроится, если банк работает по ставке 18% годовых.
Задача 29
Банк «Российский кредит» принимает
вклады до востребования по простой ставке 40% годовых. Определить сумму
начисленных процентов и сумму долга с начисленными процентами на вклад 2000 руб.,
размещенный на полгода.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 30
Вкладчик положил в банк 3000 руб.,
который выплачивает в год 6% (простых). Какая сумма будет на счету вкладчика
через 170 дней?
Задача 31
В банк было положено 150000 руб.
Сколько процентов (простых) выплачивает банк в год? Если через 2 года 9 месяцев
на счету было 270000 руб.
Задача 32
Найти
сумму начисленных простых процентов I и конечную сумму S, если
вклад P=1107.08 руб. размещен на t=10 месяцев при годовой
ставке i=70.7%.
Задача 33
Сколько
дней t понадобится, чтобы сумма в P=2228.23 рублей
«заработала» I=2.77 рублей, если она инвестируются при ставке i=23.7%
обыкновенного простого процента?
Задача 34
В банк положены на срочный
сберегательный счет 10000 руб. на 2 года по простой ставке 9% годовых с
дальнейшей пролонгацией на последующие 3 года по простой ставке 5% годовых:
а) Найдите наращенную сумму по
истечении 5 лет;
б) Найдите наращенную сумму по
истечении 5 лет, если через 2 года вклад изымается и кладется на новый счет на
3 года по простой ставке 5% годовых.
Укажите, какой вариант является
более предпочтительным а) или б)
Задача 35
Вами открыт вклад под 21% годовых.
На него начислен процентный платеж в сумме 21 тыс. руб. Найдите величину
вклада, если он был открыт на 21 год.
Задача 36
Ссуда в размере 30 000 руб. выдана
на полгода по простой ставке 100% годовых. Определить наращенную сумму.
Задача 37
Определите годовую ставку простых
процентов, при которой сумма в 5 тыс. руб. за три квартала возрастет до 6,5
тыс. руб.
Задача 38
В банк помещен капитал под 20%
годовых (обыкновенные проценты). По истечении 270 дней его величина составила
575 тыс. руб. Определить величину помещенного в банк капитала и сумму
начисленных процентов.
Задача 39
Банк
принимает депозиты на 3 месяца по ставке 15% годовых, на 8 месяцев по ставке
17% годовых и на год по ставке 19% годовых. Определить суммы, которые может
получить владелец депозита 14500 руб. Выбрать наиболее выгодный вариант
размещения вклада.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 40
Определить
срок в годах, при начислении простых процентов, по следующим данным:
Процентная
ставка 18%
Вклад –
2000 руб.
Вклад с
процентами – 10200 руб.
Задача 41
По
контракту кредитор предоставил в долг 60000 руб. Заемщик должен уплатить 70000
руб. через 90 дней. Определить доходность финансовой операции для кредитора в
виде процентной ставки i простых процентов.
Задача 42
Годовая ставка простых процентов в
банке составляет 12%. Через сколько лет вложенная сумма а) удвоится; б)
утроится?
Задача 43
В банк
положено 10000 руб., а через 2,5 года на счете было 120000 руб. Определить
ставку процентов банка.
Задача 44
За
сколько лет удвоится сумма долга, если применяется простая годовая ставка 17%?
Задача 45
При
открытии сберегательного счета при ставке 8% годовых 20 апреля на счет была
положена сумма 1 млн. рублей. Затем 5 июля этого же года было добавлено 500
тыс. руб. 10 сентября сняли сумму 750 тыс. рублей, а 20 ноября того же года
счет был закрыт.
Какую
сумму получил вкладчик при закрытии счета?
Задача 46
Какую
сумму надо положить в банк, выплачивающий 4% простых в год, чтобы получить 50
тыс. руб. а) через 4 месяца, б) через 1 год, в) через 2 года 9 месяцев?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 47
Договор
предусматривает следующие ставки простых процентов: за первый квартал j1=20%, за второй квартал j2=18%, за третий квартал j3=16%, за четвертый квартал j4=14%. Определить
коэффициент наращения за год.
Задача 48
Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.
Задача 49
На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?

Если нравится – подписывайтесь на телеграм-канал Бробанк.ру и не пропускайте новости
Высшее образование в Международном Восточно-Европейском Университете по направлению “Банковское дело”. С отличием окончила Российский экономический институт имени Г.В. Плеханова по профилю “Финансы и кредит”. Десятилетний опыт работы в ведущих банках России: Альфа-Банк, Ренессанс Кредит, Хоум Кредит Банк, Дельта Кредит, АТБ, Связной (закрылся). Является аналитиком и экспертом сервиса Бробанк по банковской деятельности и финансовой стабильности. rusanova@brobank.ru
Открыть профиль
Специалист сервиса Бробанк.ру в этой статье расскажет о простой формуле. Разберем формулу простого расчета процентов, как ею пользоваться и как провести расчет вклада. После этого останется только подставить свои цифры. Также расскажем, от чего зависят ставки по депозитам.
-
Как банки начисляют проценты по вкладам
-
Как выглядит формула простых процентов по вкладу
-
Как рассчитать вклад на специальном калькуляторе
-
Считаем вклад Тинькофф по простой формуле
-
Считаем вклад Тинькофф по сложной формуле
-
Что влияет на ставку по вкладу
Как банки начисляют проценты по вкладам
Процентная ставка — показатель доходности депозита. Сравнивая вклады в разных банках, вы смотрите на ставки. В каком она больше, тому и отдаете предпочтение. Но сам показатель процента не говорит о том, какой именно доход будет в итоге получен вкладчиком.
Ставка 8% годовых не значит, что вы получите 8% прибыли. Точный доход зависит от срока договора, формулы расчета процентов и операций, которые вкладчик проводит со счетом.
Варианты формул расчета:
- Простая. Применяется, когда банк начисляет доход по вкладу и передает его вкладчику. Начисление проводится ежемесячно, ежеквартально, ежегодно или в конце срока. Клиент получает деньги и распоряжаться ими на свое усмотрение.
- Сложная. Применяется для вкладов с капитализацией. Банк каждый месяц или квартал начисляет проценты, которые остаются на счете, увеличивая сумму вклада. В итоге доход становится выше.
Банк указывает ставку в годовом эквиваленте. Но срок вклада может составлять 3, 6, 9, 18 месяцев и так далее. Поэтому за основу можно брать доход за месяц. Например, если это ставка 8% годовых, ежемесячная прибыль составит 8/12, то есть округленно 0,67%. Такой вариант расчета прибыли можно использовать, если сумма вклада не меняется весь срок.
Как выглядит формула простых процентов по вкладу
Если по депозиту нет капитализации, проценты сразу выдают вкладчику или выплачивают по окончании срока размещения, при расчете дохода применяется формула простого процента.
Она выглядит так:
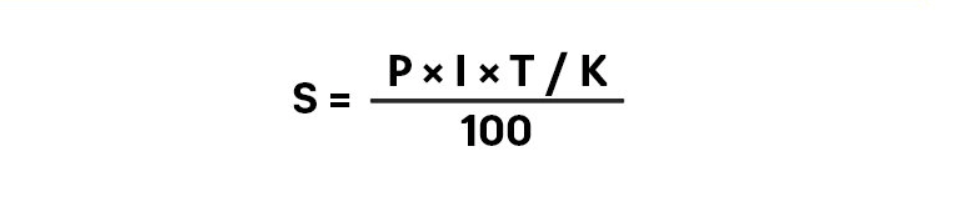
Подпись: Так выглядит формула простых процентов по вкладу.
Расшифровка формулы:
S — прибыль вкладчика
P — сумма вклада
I — процентная ставка
T — количество дней вклада
K — количество дней в году
Теперь рассчитаем прибыль вкладчика по простой формуле. Для примера возьмем депозит Газпромбанка «Копить»:
- 500 000 рублей;
- на 181 день;
- ставка для этого срока — 7,48% годовых;
- капитализации нет;
- доход клиент получит в конце срока.
Подставляем значения в формулу простых процентов по вкладу:
(500000 × 7,48 × 181 )/ 366 : 100 = 18495.
Сумма начисленных процентов составит 18 495 рублей. Именно столько получит вкладчик, если выберет вариант получения дохода одной суммой в конце срока.

Но вкладчик Газпромбанка может выбрать вариант получения процентов ежемесячно. В определенное число каждого месяца банк будет переводить ему начисленный доход на расчетный счет или карту.
В этом случае в срок подставляем количество дней в текущем месяце. Например, для мая, в котором 31 день, расчет будет таким:
(500000 × 7,48 × 31 / 366) : 100 = 3167
Если в месяце 30 дней, клиент получит 3065 рублей.
Каждый месяц потенциальный вкладчик будет получать от Газпромбанка 3167 или 3065 рублей.
Если речь о вкладе с возможностью пополнения или снятия, каждый месяц сумма может быть разной, поэтому и размер дохода не будет постоянным. Каждый месяц проводится отдельный расчет.

| Сумма от | 15 000Р |
| Проц. ставка | До 9,5% |
| Срок | До 3 лет |
| Макс. сумма | Любая |
| Пополнение | Нет |
| Снятие | Нет |
Как рассчитать вклад на специальном калькуляторе
На практике не обязательно знать формулу расчета процентов. Банки начисляют доход честно, применяя сложные или простые проценты. А вкладчики пользуются калькуляторами вкладов, в которые уже запрограммированы все формулы и схемы расчетов.
Сервис Бробанк.ру разработал калькулятор вкладов, которым все могут пользоваться бесплатно. Для расчетов переходите на страницу калькулятора.
Он выглядит так:
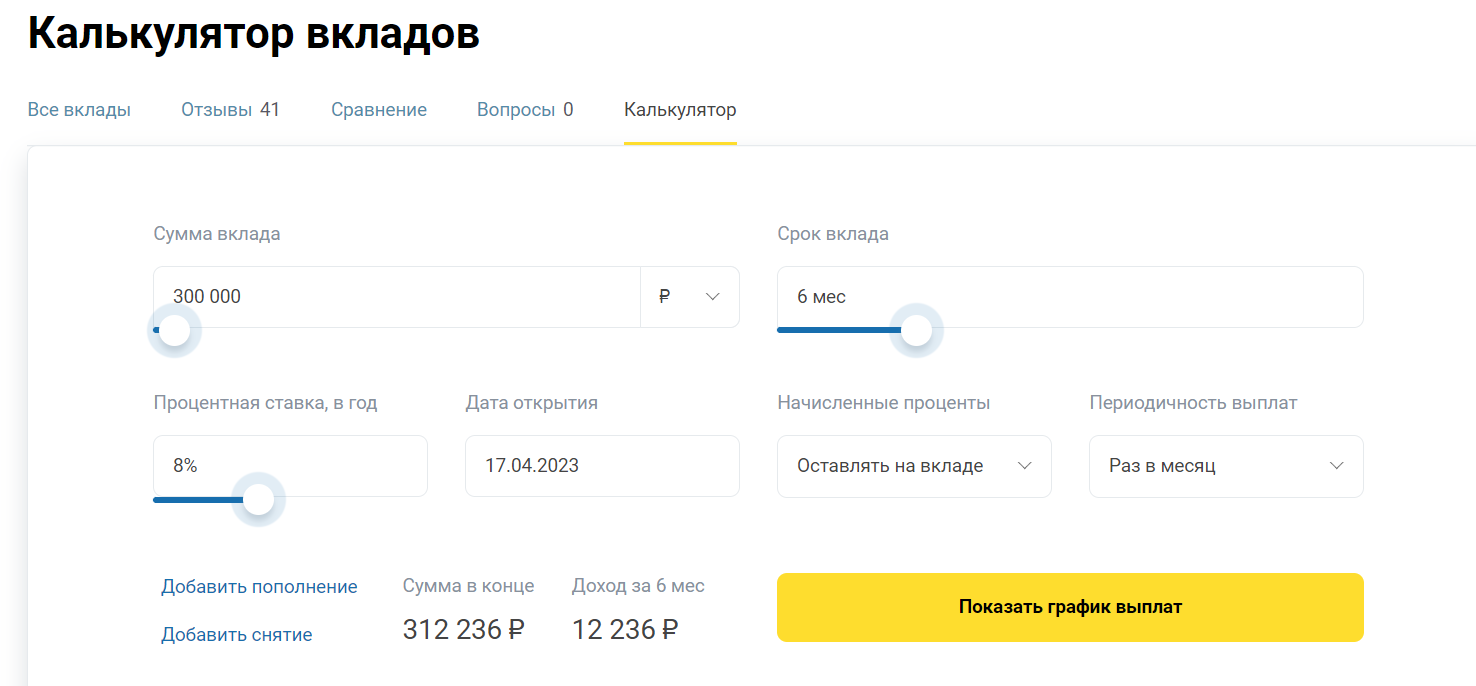
Так выглядит калькулятор расчета доходности вкладов на Бробанк.ру.
Для верного расчета определенного вклада внимательно изучите сетку тарифов. Не используйте процент, указанный как максимальный. В тарифах найдете точное значение для выбранного срока.
Считаем вклад Тинькофф по простой формуле
Например, вас заинтересовал вклад Тинькофф, годовая ставка в котором зависит от срока и от наличия у клиента подписки ПРО.
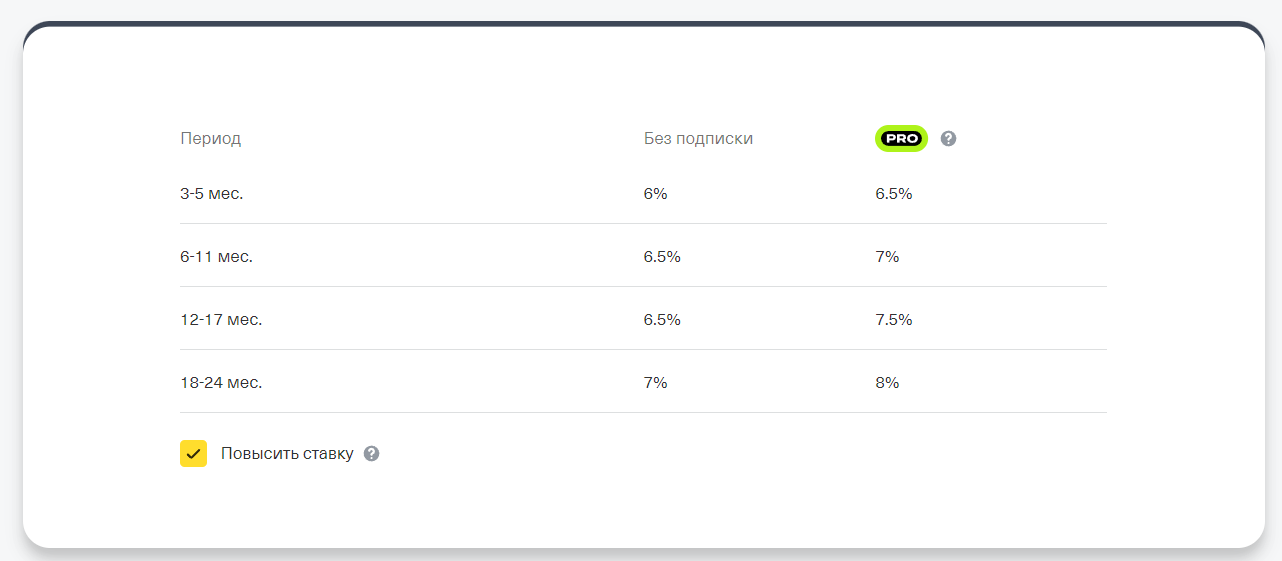
Ставки по вкладам в банке Тинькофф на момент создания материала — на апрель 2023 года.
Рассчитаем на универсальном калькуляторе доходность вклада Тинькофф со следующими параметрами:
- размер вложений — 500 000 рублей;
- договор заключается на 18 месяцев;
- у клиента нет подписки ПРО, ставка — 7%;
- выплата процентов — раз в месяц.
Вносим эти данные в калькулятор, и сразу видно, какую прибыль принесет открытие депозита в Тинькофф на 1,5 года — 52 644 рубля.
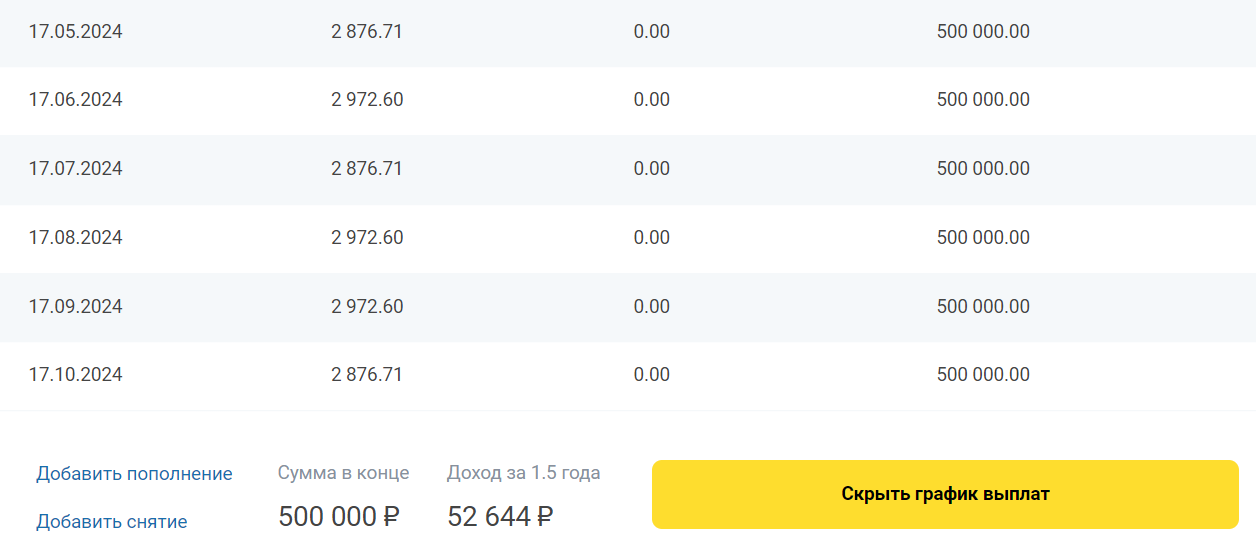
Пример расчета вклада Тинькофф на калькуляторе Бробанк по формуле простого процента.
Считаем вклад Тинькофф по сложной формуле
С капитализацией калькулятор считает прибыль по формуле сложных процентов. В этом случае в опциях выбирайте вариант «Оставлять проценты на вкладе». Расчет процентов будет таким:
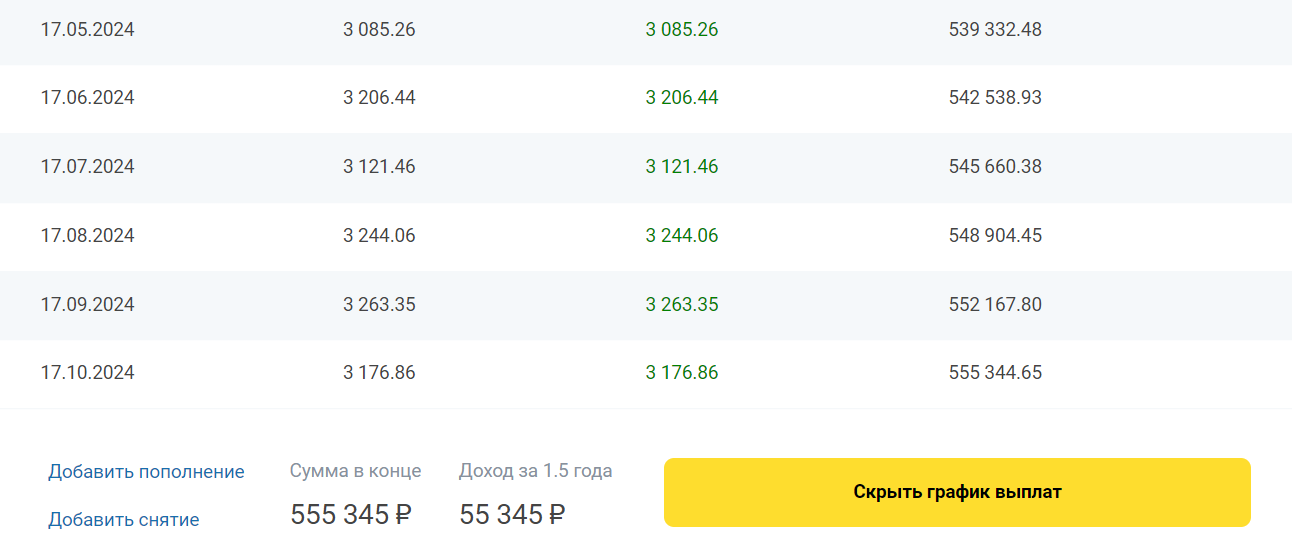
Пример расчета вклада Тинькофф на калькуляторе Бробанк по формуле сложного процента.
С капитализацией доход составит 55 345 рублей, без нее — 52 544. Делаем вывод — сложный вариант начисления процентов более выгодный для вкладчика, чем простой. По возможности лучше выбирайте программы с капитализацией.

| Сумма от | 50 000Р |
| Проц. ставка | До 8% |
| Срок | До 2 лет |
| Макс. сумма | 30 млн руб. |
| Пополнение | Возможно |
| Снятие | Возможно |
Что влияет на ставку по вкладу
На прибыль по вкладу влияет не формула расчета процентов, а характеристики вклада и сетка тарифов по программе. Наиболее выгодный вариант размещения средств — классический вклад без снятия и пополнения. Менее выгодный — с частичным снятием.
Ставки по вкладу зависят:
- от срока. Для каждого возможного срока по программе может быть установлена своя ставка;
- от суммы на счете. Например, если на счете лежат 100 000 рублей, процент один, а если 1 000 000 — другой;
- от схемы выплаты процентов: ежемесячно, в конце срока, сразу наперед при открытии счета;
- от клиента. Зарплатным клиентам банки часто увеличивают процент;
- от способа открытия вклада. Некоторые банки увеличивают ставку, если клиент открывает депозит онлайн.

Так что, смотрите не на формулу расчетов процентов, а на сетку тарифов по выбранной программе. А для анализа дохода используйте универсальный калькулятор вкладов на Бробанк.ру — он считает по тем же простым и сложным формулам.
Частые вопросы
Когда банки делают расчет процентов по вкладу по простой формуле?
Если речь о вкладе без капитализации, банк рассчитывает прибыль, когда вкладчик получает проценты на руки, или они выплачиваются банком в конце срока.
Какой вариант расчета выгоднее?
По сложной формуле расчет более выгоден для вкладчика. Если он не забирает проценты, они ежемесячно суммируются с телом вклада и прибыль становится больше.
Можно ли при открытии вклада выбрать формулу расчета процентов?
Нет, это происходит автоматически. Если вклад без капитализации, используется простая формула. Если с ней — сложная.
По какой формуле делается расчет после пролонгации?
Если в предыдущий период расчет велся по простой формуле, после пролонгации ничего не изменится. Договор продлевают на тех же условиях, поменяться может только ставка — устанавливается та, что действует на день пролонгирования.
Можно ли изменить схему начисления процентов?
Нет. Какие условия были установлены при заключении договора, такие и будут действовать весь срок вклада.
Комментарии: 0
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
