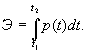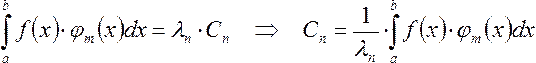Как найти норму сигнала

Тема 2:  метрология  сигналов

Физическая величина более точно определяется уравнением, чем измерением.

Макс Планк (XVIII-XIX в).

(Немецкий физик – теоретик).

Теоретикам свойственно намекать о важности своих занятий. Сам себя не похвалишь, как оплеванный ходишь. Между тем, уравнение только математическая модель физической величины. А без измерений понятия точности вообще не существует. 

Борис Старцев (XX в).

(Уральский геофизик – практик).

Содержание:  2.1. Пространство сигналов. Линейное пространство сигналов. Координатный базис пространства. Норма сигналов. Метрика сигналов. 2.2. Мощность и энергия сигналов. Понятия мощности и энергии сигналов. Скалярное произведение сигналов. 2.3. Обобщенный ряд Фурье. Ортогональные сигналы. Разложение сигнала в ряд Фурье. Ортонормированные системы функций. Разложение энергии сигнала.  2.4.  Функции  корреляции  сигналов. Корреляционные функции сигналов.  Взаимная корреляционная функция. Литература.

В данной теме метрология сигналов рассматривается, в основном, на уровне понятий и базовых определений, предваряя их более подробное изучение в дальнейших темах курса. Это объясняется тем, что при детальном изучении каких-либо характеристик или свойств сигналов их рассмотрение не может выполняться в отрыве от других метрологических характеристик рассматриваемых типов сигналов и требует определенной ориентировки в общей метрологии сигналов, хотя бы на уровне понятий.

Рекомендуемые материалы

2.1.  Пространство сигналов [1,3,16].

Важнейшее свойство аналоговых и дискретных сигналов заключается в том, что их линейные комбинации также являются аналоговыми или дискретными сигналами. Линейные комбинации цифровых сигналов, в силу их ограничения по разрядности, в принципе относятся к разряду нелинейных операций, однако последним фактором можно пренебречь, если ошибки, которые вносятся в результаты наблюдений при квантовании отсчетов, достаточно малы по сравнению с шумами зарегистрированной информации.  При дискретизации и квантовании данных непосредственно на входах в ЭВМ последнее выполняется практически всегда, поскольку ошибки определяются разрядностью ЭВМ и программными системами обработки данных, которые обычно не ниже 6-12 десятичных разрядов.

Линейное пространство сигналов.  Пусть L{s₁(t), s₂(t), …}- множество сигналов, которые имеют какие-то общие свойства и определенную структуру связи между сигналами. Например, множество может состоять из сигналов вида s_n(t) = A_ncos(w_nt+j_n)  – гармонических колебаний с определенными значениями амплитуд, частот и начальных фаз. Путем введения  структурных ограничений множество сигналов может быть превращено в функциональное пространство сигналов. Так, множество сигналов L образует линейное пространство сигналов,  если для него справедливы следующие аксиомы:

1. Для любых  сигналов u(t) Î L и v(t) Î L  существует их сумма s(t) = u(t)+v(t), которая также содержится в L, при этом операция суммирования коммутативна: u(t)+v(t) = v(t)+u(t), и ассоциативна: u(t)+(v(t)+x(t)) = (u(t)+v(t))+x(t).

2. Для любого сигнала  s(t) Î L и числа  a определен сигнал y(t) = as(t), у(t) Î L.

3. Множество L содержит такой нулевой элемент Æ, что для всех сигналов u(t) Î L выполняется равенство u(t)+Æ = u(t).

Сигналы могут описываться как вещественными, так и комплексными функциями, и линейные пространства также могут быть вещественными или комплексными.

Множество L, для которого выполняются данные аксиомы, при анализе сигналов и систем может рассматриваться как специальным образом сконструированное многомерное (в пределе – бесконечномерное) геометрическое пространство. Сигналы таких линейных пространств часто называют векторами в силу аналогии их свойств со свойствами векторов. Соответственно, для математического анализа систем и сигналов в линейном пространстве может использоваться математика векторов.

Пример. Множество сигналов L состоит из импульсных сигналов произвольной формы с амплитудой не более 10 вольт. Образуют ли эти сигналы линейное пространство?

Нет, не образуют, так как не выполняется, по крайней мере, первая аксиома линейного пространства (сумма двух сигналов с амплитудой более 5 вольт превышает 10 вольт). Требуются дополнительные структурные ограничения по параметрам сигналов.

Координатный базис пространства. В пространстве сигналов можно выделить координатный базис пространства – подмножество векторов {е₁, е₂, е₃, …} со свойствами координатных осей, по которым можно разложить произвольный сигнал, принадлежащий линейному пространству.

Совокупность векторов e_i пространства L является линейно независимой и образует координатный базис пространства, если равенство a_ie_i = Æ  выполняется только в случае одновременного обращения в нуль всех числовых коэффициентов a_i. При этом произвольный сигнал s(t) может быть разложен по координатному базису e_i  в виде

s(t) =с_ie_i,                                                  (2.1.1)

где числа с_i – проекции сигнала s(t) на координатный базис.

   Пример. 

   Линейное пространство образовано сигналами, которые описываются многочленом вида

   s(t) =c_ntⁿ.

   Координатным базисом в пространстве является система одночленов

   {е₀ = 1, е₁ = t, e₂ =  t², … , е_n = tⁿ}.

Норма сигналов. Линейное пространство сигналов L является нормированным, если каждому сигналу пространства однозначно сопоставлено число ||s(t)|| – норма (norm) сигнала, и выполняются следующие аксиомы:

1. Норма неотрицательна и равна нулю тогда и только тогда, когда сигнал равен нулю (||s(t)|| = Æ, при s(t) = Æ).

2. Для любого числа b должно быть справедливо равенство: ||bs(t)|| = |b| × ||s(t)||.

3. Если v(t) и u(t) – сигналы из пространства L, то должно выполняться неравенство треугольника: ||v(t)+u(t)|| £ ||v(t)|| + ||u(t)||.

В линейном пространстве сигналов норма является аналогом длины векторов. В математике существуют различные формы норм. Для анализа сигналов чаще всего используются квадратичные нормы:

||s(t)|| =.                                     (2.1.2)

            Соответственно, для дискретных сигналов:

||s(t)|| =.                                     (2.1.2′)

            Для комплексных сигналов:

||s(t)|| =,                               (2.1.2”)

где s*(t) – величины, комплексно сопряженные с s(t).

Метрика сигналов. Линейное пространство сигналов L является метрическим, если каждой паре сигналов u(t) Î L и v(t) Î L однозначно сопоставляется неотрицательное число r(u(t),v(t)) –  метрика (metric) или расстояние между векторами, и выполняются аксиомы:

1. r(u(t),v(t)) = r(v(t),u(t)) – рефлексивность метрики.

2. r(u(t),u(t)) = 0  для любых  u(t) Î L.

3. r(u(t),v(t)) £ r(u(t),a) + r(a,v(t)) для любых  a Î L.

Метрика определяется нормой разности двух сигналов:

r(u(t),v(t)) = || u(t) – v(t) ||.                                      (2.1.3)

В свою очередь норму можно отождествлять с расстоянием от выбранного элемента пространства до нулевого:  ||u(t)|| = r(u(t),Æ).

По метрике сигналов можно судить, например, о том, насколько точно один сигнал может быть аппроксимирован другим сигналом или насколько изменяется выходной сигнал относительно входного при прохождении через какое-либо устройство.

Пример.  Сигнал на интервале (0,Т) представляет собой половину периода синусоиды амплитудой A:  s(t) = A×sin(pt/T),  0 £ t £ T. Требуется аппроксимировать сигнал прямоугольным импульсом  п(t).

Если принять амплитуду импульса п(t) равной В, то квадрат расстояния между сигналами:  r²(s,п) =(A sin(pt/T)-В)² dt = A²T/2 – 4ABT/p + B²T.

Для решения задачи требуется найти минимум выражения r²(s,п). Дифференцируем полученное выражение по В, приравниваем нулю и, решая относительно В, находим значение экстремума: В = 2A/p » 0.64А. Это искомое значение минимума функции r²(s,п), так как вторая производная функции по В положительна. При этом минимальное значение метрики: r_min » 0.31A. Вычислим нормы сигналов при А = 1:

Е_s = А²sin² (pt/T) dt = A² T/2 = 10.  Норма:  ||s(t)|| == 0.707 A » 3.16.

Е_п = B²dt = B² T » 8.1.  Норма:  ||п(t)|| = = B » 2.85.

2.2.  Мощность и энергия сигналов [1,3,16].

Понятия мощности и энергии в теории сигналов не относятся к характеристикам каких-либо физических величин сигналов, а являются их количественными характеристиками, отражающими определенные свойства сигналов и динамику изменения их значений (отсчетов) во времени, в пространстве или по любым другим аргументам.

Для произвольного, в общем случае комплексного,  сигнала s(t) = a(t)+jb(t), где а(t) и b(t) – вещественные функции, мгновенная мощность (instantaneous power) сигнала по определению задается выражением:

            w(t) = s(t)s*(t) = [a(t)+jb(t)][(a(t)-jb(t)] = a²(t)+b²(t) = |s(t)|²,                   (2.2.1)

т.е. функция распределения мгновенной мощности по аргументу сигнала равна квадрату функции его модуля, для вещественных сигналов – квадрату функции амплитуд.

Энергия сигнала (также по определению) равна интегралу от мощности по всему интервалу существования или задания сигнала. В пределе:

                                               Е_s =w(t)dt =|s(t)|²dt.                                       (2.2.2)

По существу, мгновенная мощность является плотностью мощности сигнала, так как измерения мощности возможны только через энергию, выделяемую на интервалах ненулевой длины:

w(t) = (1/Dt)|s(t)|²dt.

Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.

Как правило, сигналы изучаются на определенном интервале Т, для периодических сигналов – в пределах одного периода Т, при этом средняя мощность (average power) сигнала:

                                   W_T(t) = (1/T)w(t) dt = (1/T)|s(t)|² dt.                              (2.2.3)

Понятие средней мощности может быть распространено и на незатухающие сигналы, энергия которых бесконечно велика. В случае неограниченного интервала Т строго корректное определение средней мощности сигнала должно производиться по формуле:

                                                             W_s = w(t) dt.                                         (2.2.3′)

Квадратный корень из значения средней мощности характеризует действующее (среднеквадратическое) значение сигнала (root mean sqare, RMS).

Применительно к электрофизическим системам, данным понятиям мощности и энергии соответствуют вполне конкретные физические величины. Допустим, что функцией s(t) отображается электрическое напряжение на резисторе, сопротивление которого равно R Ом. Тогда рассеиваемая в резисторе мощность, как известно, равна (в вольт-амперах):

w(t) = |s(t)|²/R,

а полная выделенная на резисторе тепловая энергия определяется соответствующим интегрированием мгновенной мощности w(t) по интервалу задания напряжения s(t) на резисторе R. Физическая размерность мощности и энергии в этом случае определяется соответствующей физической размерностью функции напряжения s(t) и сопротивления резистора R. Для безразмерной величины s(t) при R=1 это полностью соответствует выражению (2.2.1). В теории сигналов в общем случае сигнальные функции s(t) не имеют физической размерности и могут быть формализованным отображением  любого процесса или распределения какой-либо физической величины, при этом понятия энергии и мощности сигналов используются в более широком смысле, чем в физике. Они представляют собой специфические метрологические характеристики сигналов.

Из сравнения выражений (2.1.2) и (2.2.2) следует, что энергия и норма сигнала связаны соотношениями: 

E_s = ||s(t)||²,         ||s(t)|| =                                  (2.2.4)

Пример.   Цифровой сигнал задан функцией  s(n) = {0,1,2,3,4,5,4,3,2,1,0,0,0,0….}.

Энергия сигнала:  E_s = s²(n) = 1+4+9+16+25+16+9+4+1 = 85.    Норма:  ||s(n)|| = » 9.22

Скалярное произведение сигналов. Вычислим энергию суммы двух произвольных сигналов u(t) и v(t):

E =[u(t)+v(t)]² dt = E_u + E_v + 2u(t)v(t) dt.                              (2.2.5)

            Как следует из этого выражения, энергии сигналов (а равно и их мощности), в отличие от самих сигналов, в общем случае не обладают свойством аддитивности. Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию:

E_uv = 2u(t)v(t) dt.                                                (2.2.6)

По аналогии с математикой векторов интеграл выражения (2.2.6) называют скалярным произведением вещественных сигналов:

    П_uv = (u(t),v(t)) =u(t)v(t) dt = ||u||×||v|| cos j,                           (2.2.7)

Отсюда, косинус угла между сигналами:

cos j = П_uv/(||u||×||v||).                                               (2.2.8)

Скалярное произведение обладает следующими свойствами:

1. (u,v) ³ 0;

2. (u,v) = (v,u);

3. (au,v) = a(u,v), где а – вещественное число;

4. (u+v, a) = (u,a) + (v,a).

Линейное пространство с таким скалярным произведением называется гильбертовым пространством Н (второе распространенное обозначение – L₂). В нем справедливо фундаментальное неравенство Коши-Буняковского:

|П_uv| £ ||u||×||v||.                                              (2.2.9)

            Для комплексного гильбертова пространства скалярное произведение вычисляется по формуле:

    П_uv =u(t)v*(t) dt.                                           (2.2.7′)

Пример.   Имеется два смещенных во времени прямоугольных импульса с одинаковой амплитудой и длительностью:  s₁(t) = 2 при 0 £ t £ 5, s₁(t) = 0 при других t; и s₂(t) = 2 при 4 £ t £ 9, s₂(t) = 0 при других t.

Энергии сигналов одинаковы:  ||s₁||² = ||s₂||² = s₁²(t)dt =s₂²(t)dt = 20.

Скалярное произведение:  (s₁,s₂) = s₁(t) s₂(t) dt = 8.

         Отсюда имеем:  cos j = (s₁,s₂)/ (||s₁||×||s₂||) = 8/20 = 0.4  и j » 1.16 радиан » 66^о

Скалярное произведение определяет также расстояние между сигналами (метрику сигналов). Для квадрата метрики сигналов имеем:

r²(u,v) =[u(t)-v(t)]² dt = E_u + E_v – 2×||u||×||v|| cos j.

            При j = 0 (cos j = 1) сигналы “совпадают по направлению” и расстояние между ними минимально. При j = p/2 (cos j = 0) сигналы “перпендикулярны друг другу”, иначе говоря – ортогональны, и проекции сигналов друг на друга равны 0. При j = p (cos j = -1) сигналы “противоположны по направлению” и расстояние между сигналами максимально. Фактор расстояния между сигналами играет существенную роль при их селекции в многоканальных системах. Если функции u(t) и v(t) являются случайными, то значение cos j играет роль коэффициента корреляции между случайными процессами U(t) и V(t).

Дискретные сигналы обычно рассматриваются в пространстве Евклида (обозначение пространства – R₂). Скалярное произведение двух сигналов в пространстве Евклида – число:

 П_uv = (u_k,v_k) =u_kv_k,

где n – размерность пространства. При n = 3 это математический прообраз реального трехмерного пространства, в котором сигналы u и v отображаются точками этого пространства.

При обработке данных используются также понятия мощности взаимодействия двух сигналов x(t) и y(t):

      w_xy(t) = x(t) y*(t),                                            (2.2.10)

      w_yx(t) = y(t) x*(t),

      w_xy(t) = w*_yx(t).

Для вещественных сигналов:

                                                           w_xy(t) = w_yx(t) = x(t) y(t).                                      (2.2.10′)

С использованием выражений (2.2.10) интегрированием по соответствующим интервалам вычисляются значения средней мощности взаимодействия сигналов на определенных интервалах Т и энергия взаимодействия сигналов.

2.3.  Обобщенный  ряд  Фурье [1,3,11,16].

Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение (и соответственно нулевую энергию взаимодействия):

П_uv =u(t)v(t) dt = 0.

На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевая энергия взаимодействия двух верхних сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух нижних – взаимным расположением (ненулевые значения сигналов не имеют общих точек).

Из ортогональности по энергии всегда следует ортогональность сигналов по мощности, но не наоборот. Условия ортогональности по мощности и энергии выполняются одновременно только на конечных временных интервалах, при этом энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности.

Совокупность функций {u₀, u₁, u₂, …}, в пределе – бесконечную, называют системой ортогональных функций на отрезке (t₁,t₂), если на этом отрезке данные функции взаимно ортогональны, т.е. выполняется условие:

П_uv =u_i(t)u_j(t) dt = 0,   i = 1,2,…,   j = 1,2,…,  i ¹ j.

Систему ортогональных функций на интервале (t₁,t₂) называют ортонормированной (orthonormal functions), если все функции системы имеют единичную норму, т.е. выполняются условия:

П_uu =u_i²(t) dt = 1,    ||u_i|| == 1,        i = 1,2,….

            Система ортогональных функций, для которой данное условие не выполняется, всегда может быть превращена в ортонормальную путем нормировки, т.е. деления всех функций на их норму. В линейном пространстве сигналов системы ортогональных функций могут использоваться в качестве координатных базисных функций.

Разложение сигнала в ряд Фурье.  Произвольный сигнал s(t) Î H, заданный на интервале (t₁,t₂), может быть разложен по упорядоченной системе ортогональных базисных функций u_i(t)  в обобщенный ряд Фурье:

         s(t) =c_iu_i(t).                                                (2.3.1)

Для нахождения значений коэффициентов с_i умножим обе части данного выражения на базисную функцию u_k(t) с произвольным номером k и проинтегрируем результаты по переменной t, при этом получим:

s(t)u_k(t) dt =c_iu_iu_k dt.

            С учетом ортогональности функций u(t), в правой части этого равенства остается только один член суммы с номером i = k, который представляет собой проекцию сигнала – вектора на соответствующее базисное направление:

      c_k = s(t)u_k(t) dt.                                              (2.3.2)

            При практическом использовании количество членов ряда (2.3.1) ограничивается определенным значением N, при этом для любого значения N совокупность коэффициентов c_i обеспечивают наименьшее по средней квадратической погрешности приближение к заданному сигналу.

            В геометрической интерпретации коэффициенты с_i представляют собой проекции вектор – сигнала s(t) на соответствующие базисные направления u_i(t), т.е. координаты вектора s(t) в N-мерном пространстве (в пределе – бесконечномерном). Соответственно, энергия взаимодействия двух сигналов x(t) и y(t) может вычисляться по скалярному произведению их координатных проекций, которое равно:

П_xy = x(t)y(t) dt =a_iu_i(t)b_ju_j(t)dt =a_i×b_i.                  (2.3.3)

            Косинус угла между векторами x(t) и y(t) с использованием выражения (2.2.8):

    cos j = a_i×b_i /(||x(t)||×||y(t)||).                                       (2.3.4)

Возможность разложения непрерывных сигналов в обобщенные ряды Фурье имеет огромное принципиальное значение, так как позволяет вместо изучения несчетного множества точек сигнала ограничиться счетной системой коэффициентов ряда.

К системам базисных функций, которые используются при разложении сигналов, предъявляют следующие основные требования:

            – для любого сигнала ряды разложения должны сходиться;

            – при ограничении ряда по уровню остаточной погрешности расхождения с заданным сигналом количество членов ряда должно быть минимальным;

            – функции должны иметь достаточно простую аналитическую форму;

            – коэффициенты разложения должны вычисляться относительно просто.

            Согласно теореме Дирехле, любой сигнал s(t), имеющий конечное число точек нарушения непрерывности первого рода и конечный по энергии на интервале (t₁,t₂), может быть разложен по системе ортонормальных функций, если существуют интегралы модуля сигнала и модуля его первой производной:

|s(t)| dt    и   |s'(t)| dt.

Ортонормированные системы функций хорошо известны в математике. Это полиномы Эрмита, Лежандра, Чебышева, функции Бесселя, Лагерра и целый ряд других. При спектральном анализе и обработке сигналов  в основном используются два вида ортонормированных функций: гармонические функции и функции Уолша.

Функции ортонормированного базиса u₀,u₁,u₂,… на интервале [0,T], в пределе – бесконечном, на основе гармонических колебаний с кратными частотами приводятся ниже, вид первых пяти функций, включая постоянную составляющую u₀, показан на рис. 2.3.2.

u₀ = 1/,     u_к(t) =sin(к2pt/T),     u_к(t) = cos(к2pt/T),     к = 1,2,3, …

В качестве базисных функций частотного разложения в общем случае принимаются комплексные экспоненциальные функции exp(pt) при p = jf (преобразование Фурье) и p =  s+jf (преобразование Лапласа), от которых с использованием формул Эйлера

exp(jwt) = cos(wt) + j sin(wt),        exp(-jwt) = cos(wt) – j sin(wt),

cos(wt) = [ехр(jwt)+exp(-jwt)]/2,      sin(wt) = [ехр(jwt)-exp(-jwt)]/2j

всегда можно перейти к синус-косинусным функциям. Термин “частотного” обязан своим происхождением независимой переменной данного разложения временных сигналов, которая измеряется в единицах, обратных единицам времени, т.е. в единицах частоты f = 1/|t|. Однако понятие частотного преобразования не следует связывать только с временным представлением сигналов, т.к. математический аппарат преобразования не зависит от физического смысла переменных. Так, например, при переменной “х”, как единице длины, значение f будет представлять собой пространственную частоту – число периодических изменений сигнала на единице длины с размерностью 1/|х|.

Ортонормированная система функций Уолша, по существу, является предельной модификацией системы периодических функций с кратными частотами, при этом функции принимают значения только ±1. Пример четырех первых функций Уолша на интервале Т от –0,5 до 0,5 приведен на рис. 2.3.3. Ортогональность и нормированность функций следует из принципа их построения. Стандартное математическое обозначение функций Уолша:  wal(k,q), где k = 0,1,2, … – порядковый номер функции, q = t/T – безразмерная координата (нормированная на интервал Т независимая переменная).

Наряду с функциями Уолша применяются также две связанные с ними системы: четные и нечетные функции cal(n,q) = wal(2n,q),  – аналогичные косинусам, и sal(n,q) = wal (2n-1,q), – аналогичные синусам.

При разложении сигналов форма спектров Уолша практически тождественна спектрам гармонических функций.

Разложение энергии сигнала. Допустим, что сигнал s(t) разложен в обобщенный ряд Фурье (2.3.1). Вычислим энергию сигнала непосредственной подстановкой выражения (2.3.1) в выражение (2.2.2):

         E_s =s²(t) dt =c_ic_ju_iu_j dt = c_ic_j u_iu_j dt.             (2.3.5)

В этом выражении в силу ортонормированности базисной системы отличны от нуля только члены с номерами i = j. Отсюда:

E_s =s²(t) dt =c_i²,                                            (2.3.6)

т.е. при корректном разложении сигнала в обобщенный ряд Фурье энергия сигнала не изменяется и равна сумме энергии всех составляющих ряда. Это соотношение называют равенством Парсеваля.

2.4.  Функции  корреляции  сигналов [1, 25].

Функции корреляции сигналов применяются для интегральных количественных оценок формы сигналов и степени их сходства друг с другом.

Автокорреляционные функции (АКФ) сигналов (correlation function, CF). Применительно к детерминированным сигналам с конечной энергией АКФ является количественной интегральной характеристикой формы сигнала и представляет собой интеграл от двух копий сигнала s(t), сдвинутых относительно друг друга на время t:

B_s(t) = s(t) s(t+t) dt.                                         (2.4.1)

            Как следует из этого выражения, АКФ является скалярным произведением сигнала и его копии в функциональной зависимости от переменной величины значения сдвига t. Соответственно, АКФ имеет физическую размерность энергии, а при t = 0 значение АКФ непосредственно равно энергии сигнала и является максимально возможным (косинус угла взаимодействия сигнала с самим собой равен 1):

B_s(0) =s(t)² dt = E_s.

Функция АКФ является непрерывной и четной. В последнем нетрудно убедиться заменой переменной t = t-t в выражении (2.4.1):

B_s(t) = s(t) s(t-t) dt =  s(t-t) s(t) dt = B_s(-t).

            С учетом четности, вычисление АКФ обычно производится только для положительных значений t. Знак +t в выражении (2.4.1) означает, что при увеличении значений t от нуля копия сигнала s(t+t) сдвигается влево по оси t. На практике сигналы обычно также задаются на интервале положительных значений аргументов от 0-Т, что дает возможность продления интервала нулевыми значениями, если это необходимо для математических операций. В этих границах вычислений более удобным является сдвиг копии сигнала влево по оси аргументов, т.е. применение в выражении (2.4.1) функции s(t-t):

B_s(t) = s(t) s(t-t) dt.                                         (2.4.1′)

По мере увеличения значения величины сдвига t для финитных сигналов временное перекрытие сигнала с его копией уменьшается, а, соответственно, косинус угла взаимодействия и скалярное произведение в целом стремятся к нулю:

 = 0.

Пример.   На интервале (0,Т) задан прямоугольный импульс с амплитудным значением, равным А. Вычислить автокорреляционную функцию импульса.

При сдвиге копии импульса по оси t вправо, при 0≤t≤T сигналы перекрываются на интервале от t до Т. Скалярное произведение:

B_s(t) =A² dt = A²(T-t).

При сдвиге копии импульса влево, при -T≤t<0 сигналы перекрываются на интервале от 0 до Т-t. Скалярное произведение:   

B_s(t) =A² dt = A²(T+t).

         При |t| > T сигнал и его копия не имеют точек пересечения и скалярное произведение сигналов равно нулю (сигнал и его сдвинутая копия становятся ортогональными).

         Обобщая вычисления, можем записать:

B_s(t) = .

            В случае сигналов с бесконечной энергией и периодических сигналов АКФ вычисляется по определенному интервалу (периоду) Т, с усреднением скалярного произведения и его сдвинутой копии в пределах этого интервала (одного периода для периодических):

B_s(t) = (1/Т)s(t) s(t-t) dt.                                  (2.4.2)

            При t=0 значение АКФ в этом случае равно не энергии, а средней мощности сигналов в пределах интервала Т.  АКФ периодических сигналов при этом также является периодической функцией с тем же периодом Т.  Так, для сигнала s(t) = A cos(w₀t+j₀) при T=2p/w₀ имеем:

B_s(t) = A cos(w₀t+j₀) A cos(w₀(t-t)+j₀) = (A²/2) cos(w₀t).

            Отметим, что полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств КФ.

            Взаимная корреляционная функция (ВКФ) сигналов (cross-correlation function, CCF) показывает степень сходства сдвинутых экземпляров двух разных сигналов и их взаимное расположение по координате (независимой переменной), для чего используется та же формула (2.4.1), что и для АКФ, но под интегралом стоит произведение двух разных сигналов, один из которых сдвинут на время t:

B₁₂(t) = s₁(t) s₂(t+t) dt.                                      (2.4.3)

При замене переменной t = t-t в формуле (2.4.3), получаем:

B₁₂(t) =s₁(t-t) s₂(t) dt = s₂(t) s₁(t-t) dt = B₂₁(-t)

Вместе с этой лекцией читают “Наследственность и методы ее изучения”.

Отсюда следует, что для ВКФ не выполняется условие четности, а значения ВКФ не обязаны иметь максимум при t = 0. Это можно наглядно видеть на рис. 2.4.1, где заданы два одинаковых сигнала с центрами на точках 0.5 и 1.5. Вычисление по формуле (2.4.3) с постепенным увеличением значений t означает последовательные сдвиги сигнала s2(t) влево по оси времени (для каждого значения s1(t) для подынтегрального умножения берутся значения s2(t+t)).

При t=0 сигналы ортогональны и значение B₁₂(t)=0. Максимум В₁₂(t) будет наблюдаться при сдвиге сигнала s2(t) влево на значение t=1, при котором происходит полное совмещение сигналов s1(t) и s2(t+t). При вычислении значений B₂₁(-t) аналогичный процесс выполняется последовательным сдвигом сигнала s1(t) вправо по временной оси с постепенным увеличением отрицательных значений t, а соответственно значения B₂₁(-t) являются зеркальным (относительно оси t=0) отображением значений B₁₂(t), и наоборот. На рис. 2.4.2 это можно видеть наглядно.

Таким образом, для вычисления полной формы ВКФ числовая ось t должна включать отрицательные значения, а изменение знака t в формуле  (2.4.3) равносильно перестановке сигналов.

            Для периодических сигналов понятие ВКФ обычно не применяется, за исключением сигналов с одинаковым периодом, например, сигналов входа и выхода систем при изучении характеристик систем.

Энергетические характеристики сигналов

Основными
энергетическими характеристиками
сигнала s(t) являются егомощностьиэнергия.

Мгновенная
мощность p(t) для вещественного
сигнала определяется как

а
для комплексного как

где
знак ” * ” означает комплексно
сопряженную функцию.

Если
s(t) – напряжение или ток, тоp(t)
есть мгновенная мощность, выделяемая
на сопротивлении 1 Ом.

Энергия
сигнала на интервале ( t₂ ,t₁
) определяется как интеграл от
мгновенной мощности

Отношение

имеет
смысл средней на интервале ( t₂ ,t₁ ) мощности.

Для
неограниченных по времени периодических
сигналов определяют среднюю за период
мощность

Ортогональные
сигналы.
Два сигнала
называются ортогональными (orthogonal), если
имеют нулевое скалярное произведение

u(t),
v(t)
=u(t)v(t)
dt = 0.

Соответственно,
два таких сигнала в своем функциональном
пространстве являются взаимно
перпендикулярными (угол между сигналами
равен 
= 90^о),
полностью независимыми друг от друга
(некоррелированными, r = cos ,
и имеют нулевую энергию взаимодействия
(E_uv
= 0).

Рис.
2.3.1. Ортогональные сигналы.

На рисунке 2.3.1
приведены примеры взаимно ортогональных
сигналов. Нулевое скалярное произведение
двух левых сигналов обеспечивается их
формой (равна нулю сумма положительных
и отрицательных значений произведения
сигналов), а двух правых – взаимным
расположением (ненулевые значения
сигналов не имеют общих координат).

Попутно заметим,
что энергия и мощность суммы ортогональных
сигналов обладают свойством аддитивности,
т.к. имеют нулевое значение скалярного
произведения и, соответственно, нулевую
энергию взаимодействия.

Норма
сигналов
в линейном пространстве является
аналогом длины векторов, и обозначается
индексом ||s(t)|| – норма
(norm). В математике существуют различные
формы норм. При анализе сигналов обычно
используются квадратичные нормы

||s(t)|| =.
(2.1.2)

Для дискретных
сигналов:

||s(n)|| =.
(2.1.2′)

Для комплексных
сигналов

||s(t)|| =,
(2.1.2”)

где s*(t) – величины,
комплексно сопряженные с s(t).

Линейное пространство
сигналов L является нормированным, если
каждому сигналу пространства s(t)
однозначно сопоставлена его числовая
норма ||s(t)||, и выполняются следующие
аксиомы:

1. Норма неотрицательна
   (||s(t)|| ≥ 0) и равна нулю тогда и только
   тогда, когда сигнал равен нулю (||s(t)|| =
   ,
   при s(t) = ).

2. Для любого числа
   b должно быть справедливо равенство
   ||bs(t)|| = |b| 
   ||s(t)||.

3. Если v(t) и u(t) –
   сигналы из пространства L, то должно
   выполняться неравенство треугольника
   ||v(t)+u(t)|| 
   ||v(t)|| + ||u(t)||.

Пример норм для
двумерных цифровых сигналов приведен
на рис. 2.1.2.

Энергетические спектры сигналов [1].

Скалярное
произведение сигналов.Энергия
суммы двух произвольных сигналов u(t) и
v(t) определяется выражением

E
=[u(t)+v(t)]²
dt = E_u
+ E_v
+ 2u(t)v(t)
dt. (7.2.1)

Как
следует из этого выражения, энергии
сигналов, в отличие от самих сигналов,
в общем случае не обладают свойством
аддитивности. Энергия суммарного сигнала
u(t)+v(t), кроме суммы энергий составляющих
сигналов, содержит в себе и так называемую
энергию взаимодействия сигналов или
взаимную энергию

E_uv= 2u(t)v(t)
dt. (7.2.2)

Интеграл
выражения (7.2.2) для двух вещественных
сигналов является фундаментальной
характеристикой, пропорциональной
взаимной энергии сигналов. Его называют
скалярным произведениемсигналов

П_uv= (u(t),v(t)) =u(t)v(t)
dt = ||u||||v|| cos, (7.2.3)

Скалярное
произведение обладает следующими
свойствами

1. (u,v) 
   0;

2. (u,v) = (v,u);

3. (au,v) = a(u,v), где а –
   вещественное число;

4. (u+v, a) = (u,a) + (v,a).

Линейное
пространство сигналов с таким скалярным
произведением называется гильбертовым
пространствомН. С учетом того, что
cos1, в гильбертовом пространстве справедливо
неравенство Коши-Буняковского

|П_uv|||u||||v||. (7.2.4)

Для
комплексного гильбертова пространства
скалярное произведение также представляет
собой вещественное число и вычисляется
по формуле

П_uv=u(t)v*(t)
dtu*(t)v(t)
dt. (7.2.3′)

Из
выражения (7.2.3) следует, что косинус угла
между сигналами

cos
= П_uv/(||u||||v||). (7.2.5)

При
полной тождественности сигналов
(равенстве амплитуд и временных координат)
имеем = 0, cos= 1, и скалярное произведение становится
равным энергии сигналов:

П_uv=u(t)²dtv(t)²dt||u||²||v||².

Дискретные
сигналы обычно рассматриваются в
пространстве Евклида(обозначение
пространства – R₂). Скалярное
произведение двух сигналов в пространстве
Евклида:

П_uv= (u_k,v_k)
=u_kv_k,

где
n – размерность пространства.

Взаимный
энергетический спектр.Из очевидной
однозначности энергии взаимодействия
сигналов независимо от формы их
математического представления (в
динамической и частотной модели) следует
выражение для скалярного произведения
произвольных вещественных сигналов
u(t) и v(t) через спектральные плотности
сигналов U() и V()
в комплексном гильбертовом пространстве:

П_uv= (1/2)U()V*()
d(1/2)U*()V()
d. (7.2.6)

Функции

W_uv()
= U()V*(),
W_vu()
= U*()V(),
W_uv()
= W_vu*(),
(7.2.7)

для
которых справедливо выражение (7.2.6),
называется взаимными энергетическими
спектрамивещественных сигналов, и
являются функциями распределения
плотности энергии взаимодействия
сигналов (мощности взаимодействия) по
частоте.

В
общем случае, за исключением спектров
четных функций, взаимные энергетические
спектры также являются комплексными
функциями:

U()
= A_u()
+ j B_u(),
V() = A_v()
+ j B_v().

W_uv
= A_uA_v+B_uB_v+j
(B_uA_v
– A_uB_v)
= Re W_uv(w)
+ j Im W_uv().
(7.2.7′)

С
учетом четности реальной части и
нечетности мнимой части энергетических
спектров, интеграл мнимой части выражения
(7.2.7′) равен нулю, а, следовательно,
скалярное произведение сигналов всегда
является вещественным и неотрицательным,
как и энергия сигналов:

П_uv= (1/2)W_uv()
d(1/)Re
W_uv()
d.2.8)

Рис.
7.2.1. Форма и энергетические спектры
сигналов.

На
рис. 7.2.1 приведена форма двух одинаковых
сдвинутых во времени и частично
перекрывающихся лапласовских импульсов
u(t) и v(t), а также суммарный импульс
z(t)=u(t)+v(t). Плотности энергии сигналов
W(f) приведены в относительных единицах
плотности энергии суммарного сигнала
W_z(f) на
нулевой частоте.

Как
видно из графиков, плотности энергии
сигналов являются вещественными
неотрицательными функциями и содержат
только реальные части. В отличие от них,
плотность взаимной энергии сигналов
является комплексной функцией, при этом
модуль плотности по своим значениям на
шкале частот соизмерим со средними
значениями плотности энергии сигналов
на этих частотах и не зависит от их
взаимного расположения на временной
оси. Для сигналов, одинаковых по форме,
модуль взаимной плотности равен значениям
плотности энергии сигналов.

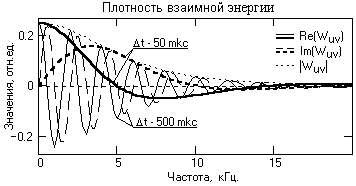
Рис.
7.2.2. Взаимные энергетические спектры
сигналов.

На
рис. 7.2.2 приведены плотности взаимной
энергии тех же сигналов при разной
величине временного сдвига t
между сигналами. Однако при постоянном
значении модуля взаимной энергии
сигналов действительная и мнимая функции
спектра мощности существенно изменяются
при изменении сдвига между сигналами.
При незначительной величине временного
перекрытия сигналов частота осцилляций
реальной и мнимой части плотности
взаимной энергии достаточно велика, а
относительный коэффициент затухания
колебаний (уменьшение амплитудных
значений от периода к периоду) достаточно
мал. Соответственно, при вычислении
скалярного произведения по формуле
(7.2.8) положительные амплитудные значения
осцилляций Re(W_uv)
практически полностью компенсируются
отрицательными значениями и результирующий
интеграл, а равно и энергия взаимодействия
сигналов (удвоенное значение скалярного
произведения), близка к нулевой (стремится
к нулю по мере увеличения сдвига между
сигналами).

При
увеличении степени взаимного перекрытия
сигналов частота осцилляций плотности
взаимной энергии уменьшается (t
= 50 mkc на рис. 7.2.2) и основным по энергии
реальной части спектра становится
центральный низкочастотный пик, площадь
которого не компенсируется площадью
последующей отрицательной полуволны
осцилляции. Соответственно, возрастает
и энергия взаимодействия сигналов. При
полном перекрытии сигналов (при нулевом
фазовом угле между сигналами) осцилляции
исчезают, и энергия взаимодействия
сигналов максимальна.

3.
Специальные математические функции
для описания сигналов (rect-функция,
sign-функция,
sinc-функция,
функция Хэвисайда (включения), функция
Дирака (дельта-функция)).

4.
Помехи радиоприёму. Классификация
помех.

Помехи

Помехами
обычно называют посторонние электрические
возмущения, накладывающиеся на
передаваемый сигнал и затрудняющие его
прием. При большой интенсивности помех
прием становится практически невозможным.

Классификация
помех:

а)
помехи от соседних радиопередатчиков
(станций);

б)
помехи от промышленных установок;

в)
атмосферные помехи (грозы, осадки);

г)
помехи, обусловленные прохождением
электромагнитных волн через слои
атмосферы: тропосферу, ионосферу;

д)
тепловые и дробовые шумы в элементах
радиоцепей, обусловленные тепловым
движением электронов.

Математически
сигнал на входе приемника можно
представить либо в виде суммы передаваемого
сигнала и помехи, и тогда помеху называют
аддитивной, либо простошумом,
либо в виде произведения передаваемого
сигнала и помехи, и тогда такую помеху
называютмультипликативной. Эта
помеха приводит к значительным изменениям
интенсивности сигнала на входе приемника
и объясняет такие явления какзамирания.

Наличие
помех затрудняет прием сигналов при
большой интенсивности помех, распознавание
сигнала может стать практически
невозможным. Способность системы
противостоять мешающему воздействию
помехи носит название помехоустойчивости.

Внешние
естественные активные помехи представляют
собой шумы, возникающие в результате
радиоизлучения земной поверхности и
космических объектов, работы других
радиоэлектронных средств. Комплекс
мероприятий, направленных на уменьшение
влияния взаимных помех РЭС, называется
электомагнитной совместимостью. Этот
комплекс включает в себя как технические
меры совершенствования радиоаппаратуры,
выбор формы сигнала и способа его
обработки, так и организационные меры:
регламентация частоты, разнесение РЭС
в пространстве, нормирование уровня
внеполосных и побочных излучений и др.

5.
Разложение произвольного сигнала по
заданной системе ортогональных функций.
Условия
ортогональности системы действительных
функций.
Интеграл
Дирихле.

Функции
φ(x)
и _Ψ(x)
называются ортогональными,если интеграл
от их произведения равен нулю.

Рассмотрим
ряд функций:
.
Система функцийназывается
ортогональной, если на отрезке от “а”
до “b” все функции попарно ортогональны.

Рассмотрим
промежуток где n=m:

Если
система функций
при
n=mимеет коэффициент,
то эта функция является ортонормальной.
Если ортогональная система функций не
ортонормальна, то ее можно получить,
произведя замену:

.

Рассмотрим
систему ортогональных функций
и
некоторой произвольной функции.
Разложим функциюв
ряд по системе ортогональных функций,
то есть предположим, что существует
разложение вида:

Определим
коэффициенты ряда. Для этого умножим
обе части равенства [1] на
и
проинтегрируем. В результате получим:

Так
как система функций ортогональна и
ортонормальна, то получили равенство
.
Выразим С_n
из уравнения:

Ряд
[1] называется обобщенным рядом Фурье,
–
коэффициентом ряда Фурье. Ряд [1] существует
тогда и только тогда, когдаявляется
периодической функцией, а система
функций–
является равномерно сходящейся.

7.
Ряд
Фурье. Разложение в ряд Фурье. Комплексная
и тригонометрическая формы ряда Фурье.
Понятие
частотного спектра.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В современной теории радиотехнических сигналов широкое применение находят геометрические представления сигналов, использующие такие понятия как пространство, вектор, расстояние, проекция и т.д. Поэтому, для уяснения сущности геометрического представления необходимо познакомиться с этими понятиями.

Как уже подчеркивалось выше, для передачи сообщений в РТИС используется множество сигналов , образующее ансамбль сигналов. Это множество может быть непрерывным (континуальным), либо дискретным (счетным). В свою очередь дискретные множества могут быть конечными, либо бесконечными. При геометрическом представлении говорят, что множество образует пространство сигналов.

Любое пространство предполагает наличие системы координат. Пространство, в котором обитает человек, характеризуется декартовой системой координат, характеризующейся наличием трех взаимно перпендикулярных координатных осей. Тогда с любой точкой пространства будут связаны три вещественных числа, которые можно рассматривать как координаты точки в пространстве.

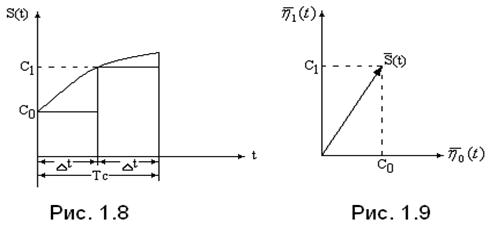
Рассмотрим как можно распространить указанные понятия на радиотехнические сигналы. В качестве примера приведем представление произвольного сигнала длительностью в виде суммы двух неперекрывающихся прямоугольных импульсов с высотой соответственно и и длительностью (рис 1.8).

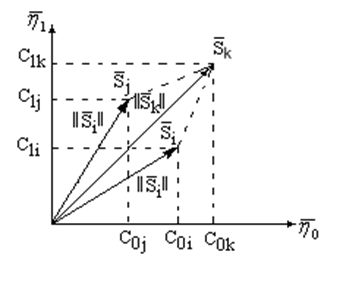
Т.к. импульсы не перекрываются во времени (проекция одного импульса на другой по оси времени равна нулю), то совокупность двух импульсов, отображающих сигнал , можно представить точкой в двумерной системе координат, образованной взаимноперпендикулярными векторами и (рис.1.9). Отрезок прямой, проведенный из начала системы координат в точку с координатами и представляет собой вектор сигнала при его данном динамическом представлении. Тогда математически его можно записать в виде

.

Если представить тремя импульсами, то сигнал будет отображаться вектором в трехмерном пространстве, четырьмя импульсами-вектором в четырехмерном пространстве, n импульсами-вектором в n-мерном пространстве. Таким образом, в общем случае сигнал отображается вектором в абстрактном n-мерном пространстве. При этом пространство может быть бесконечномерным.

Отметим, что совокупность векторов образуют координатный базис пространства. Очевидно, с изменением значений сигнала во времени длина вектора и его положение в пространстве будет также меняться.

Для дальнейшего рассмотрения геометрического представления зафиксируем момент времени , т.е. сделаем как бы фотографический снимок пространства. Это позволит на время абстрагироваться от динамики изменения сигнала и рассмотреть свойства пространства, используемого для геометрического представления. Кроме того, при характеристике пространства будем использовать его n-мерную модель, а для графических иллюстраций – двумерное пространство.

Исходя из этих предположений, вектор сигнала можно записать следующим образом

. (1.20)

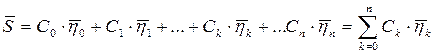
В теории радиотехнических сигналов пространство для геометрического представления должно быть линейным.

Линейное пространство обладает следующими основными свойствами:

– если векторы и принадлежат пространству , то и вектор также принадлежит этому пространству, причем (рис.1.10)

; (1.21)

Рис. 1.10

– определена операция умножения вектора на любое вещественное число , причем

; (1.22)

– пространство содержит нулевой элемент , причем

. (1.23)

Поскольку при анализе сигналов, как правило, пользуются количественными характеристиками, пространство геометрического представления должно позволять определять длину векторов для их сравнения. Длину вектора называют нормой , а пространство, в котором определена норма – нормированным пространством. Основными свойствами линейного нормированного пространства являются:

– для любого вещественного числа норма

; (1.24)

– если и – два вектора, принадлежащие линейному нормированному пространству, то:

. (1.25)

Свойство (1.25) отображает так называемое правило треугольника, известное из курса геометрии, в справедливости которого можно убедиться из рис.1.10.

В качестве нормы в теории радиотехнических сигналов используют величину

. (1.26)

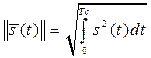
Очевидно квадрат нормы

, представляет собой энергию сигнала.

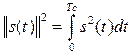
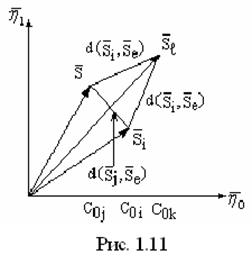
Введение понятия нормы позволяет определять длину векторов, представляющих сигналы в линейном нормированном пространстве, но не позволяет определять расстояние между векторами. Для того чтобы это стало возможным необходимо ввести понятие расстояния между векторами и , т.е. величину , называемую метрикой. Тогда линейное нормированное пространство становится метрическим.

Метрика пространства должна удовлетворять условиям:

• расстояние между одинаковыми векторами равно нулю, т.е.

; (1.27)

(1.28)

• должно выполняться правило треугольника, т.е.

. (1.29)

В теории радиотехнических сигналов в качестве метрики используют норму разности двух сигналов

. (1.30)

Нетрудно убедиться, что величина (1.30) удовлетворяет всем аксиомам метрического пространства.

И, наконец, взаимное расположение двух векторов пространстве оценивается величиной угла между ними, который определяется выражением

, (1.31)

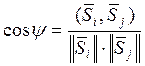
где числитель представляет собой скалярное произведение векторов.

Таким образом, для геометрического представления сигналов в радиотехнике используется линейное метрическое нормированное пространство. Если пространство конечномерное (координатный базис содержит конечное число векторов ), то такое пространство называют Евклидовым. Бесконечномерное пространство называется Гильбертовым пространством.

1