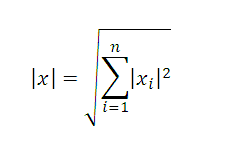Как найти норму вектора онлайн

Как найти норму вектора онлайн

Онлайн калькулятор для нахождения длины (нормы) вектора.
Найти нормированный вектор, норма вектора – длина вектора на линейном пространстве.
Построить вектор в двухмерном и трехмерном пространстве.

Скачать калькулятор

Рейтинг: 3.1 (Голосов 15)

×

Пожалуйста напишите с чем связна такая низкая оценка:

×

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке

Смотрите также

Действия с векторами Cкалярное произведение Векторное произведение Длина, модуль вектора Угол между векторами
Векторный калькулятор Сложение и вычитание Разложить вектор по базису Сумма векторов Середина отрезка
Источник

Норма вектора

Формулы, примеры, калькулятор нормы вектора

Определение 1. Норма вектора  ( эвклидова норма, модуль вектора, длина вектора)  x=(x1,x2, …xn)

Пример 1. Найти норму вектора a = (5,-2,7)

Решение. Подставляем координаты вектора, получаем норму вектора

Как нормировать вектор

Нормированный вектор – это единичный вектор по направлению. То есть, сохраняется информация только о направлении вектора:

Для того чтобы получить нормированный вектор, необходимо каждую координату исходного вектора разделить на норму вектора.

 Пример 2. Нормировать  вектор  a = (5,-2,7)

Решение. Подставляем координаты вектора, получаем нормированный вектор

Проверить правильность вычисления нормы вектора, а также найти нормированный вектор можно с помощью калькулятора.
  • 1
  • 2
  • 3
  • 4
  • 5

Категория: Аналитическая геометрия | Просмотров: 12351 | | Теги: вектор | Рейтинг: 0.0/0

Источник

Unit Converter

Enter any vector into the normalize vector calculator. The calculator will normalize this vector and display the unit vector.

  • Vector Subtraction Calculator
  • Vector Magnitude Calculator
  • Unit Vector Calculator
  • Resultant Vector Calculator

Normalizing a Vector Formula

The following formula is used to normalize a vector.

u = U / |U|

|U| = Square Root ( X^2 + Y^2+Z^2)

  • Where U is the original vector
  • |U| is the magnitude of the vector
  • u is the unit vector

Normalize Vector Definition

A vector normalization is a process of finding the unit vector of a given vector.

How to normalize a vector?

How to normalize a vector?

  1. First, calculate the magnitude of the original vector

    Using the formula above, calculate the magnitude of the original vector.

  2. Next, divide each component of the vector by the magnitude.

    For example, for a vector x,y,z, divide x by the magnitude, y by the magnitude, and z by the magnitude. The results of those divisions are your unit vector values.

Example Problem:

In the following example, a vector of (5,6,10) is given.

First, the magnitude of the vector must bed calculated. Using the formula above:

|U| = sqrt( 5^2 + 6^2+10^2)

|U| = 12. 688

Next, divide each individual component of the vector by the magnitude to normalize the vector.

X = 5 / 12.688 = .394

Y = 6 / 12.688 = .472

Z = 10 / 12.688 = .788

So the final normalized vector would be (.394,.472,.788).

FAQ

What is normalizing a vector?

Normalizing a vector is the process of turning a vector into its unit vector. This process involves dividing a vector by its magnitude. The result is a vector with the same direction, but with a magnitude of 1.

Why would you normalize a vector?

Normalizing a vector can simply problems. For example, if you want to multiply two vectors A and B, you can actually multiply their unit vectors to get the direction, then multiply that answer by the magnitudes to get the resulting vector of A * B.

normalize vector calculator
normalize vector formula

Источник

  • Customer Voice

  • Questionnaire

  • FAQ

Vector norm

[0-0] / 0 Disp-Num

BACK NEXT

The message is not registered.

BACK NEXT

Thank you for your questionnaire.

Sending completion

Back

To improve this ‘Vector norm Calculator’, please fill in questionnaire.

Age
Under 20 years old20 years old level
30 years old level40 years old level
50 years old level60 years old level or over
Occupation
Elementary school/ Junior high-school student
High-school/ University/ Grad studentA homemakerAn office worker / A public employee
Self-employed peopleAn engineerA teacher / A researcherA retired personOthers
Useful?
VeryUseful
A little Not at All
Purpose of use?
Comment/Request (Click here to report a bug).Bug report (Click here to report questionnaire.）
Calculation bug(Please enter information such as specific input values, calculation result, correct result, and reference materials (URL and documents).)
Text bug(Please enter information such as wrong and correct texts)

Your feedback and comments may be posted as customer voice.
送信

The hyperlink to [Vector norm]
Источник

Enter a vector to find the unit vector in the same direction.

Unit Vector:

Unit Vector:

Magnitude

Steps to Solve

Use the Unit Vector Formula

â = a / |a|

Step One: Solve the Magnitude

|a| = x² + y² + z²

Substitute Values and Solve

Enter vector coordinates above to see the solution here

Step Two: Divide by the Magnitude

Divide each vector component by the magnitude.

Substitute Values and Solve

Enter vector coordinates above to see the solution here

Learn how we calculated this below


scroll down

On this page:

  • Unit Vector Calculator

  • How to Find a Unit Vector

  • Unit Vector Formula

  • How to Use the Unit Vector Formula

How to Find a Unit Vector

A unit vector is a vector with a length, or magnitude, of 1. You can scale a vector to a unit vector by reducing its length to 1 without changing its direction.

This is often referred to as vector normalization.

Unit Vector Formula

To normalize a vector to a unit vector, use the following formula:

û = u / |u|

Thus, the unit vector û of vector u is equal to each component of vector u divided by its magnitude |u|.

How to Use the Unit Vector Formula

The first step to scale a vector to a unit vector is to find the vector’s magnitude. You can use the magnitude formula to find it.

|u|= x² + y² + z²

The magnitude |u| of vector u is equal to the square root of the sum of the square of each of the vector’s components x, y, and z.

Then, divide each component of vector u by the magnitude |u|. The resulting components form the unit vector.

For example, given a vector (3, 5, 8), let’s find the unit vector.

Start by solving the magnitude.

|u|= 3² + 5² + 8²
|u|= 9 + 25 + 64
|u|= 98

Then, divide each vector coordinate by the magnitude 98.

xû = 3 / √98 = 0.303
yû = 5 / √98 = 0.505
zû = 8 / √98 = 0.808

So, the unit vector û is (0.303, 0.505, 0.808).

û = (0.303, 0.505, 0.808)

Источник

Добавить комментарий