Содержание:
Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):
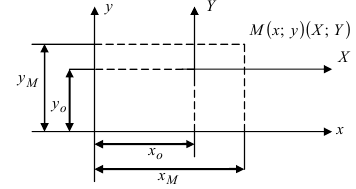
Рис. 46. Параллельный перенос одной системы координат относительно другой системы.
Систему координат 
Пример:
Дана точка М(3;2) и начало новой системы координат  Вычислить положение точки М в новой системе отсчета.
Вычислить положение точки М в новой системе отсчета.
Решение:
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 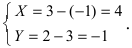 Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).
Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).
2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 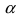 (Рис. 47):
(Рис. 47): 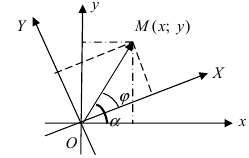
Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны 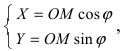 а координаты этой точки в старой системе координат равны
а координаты этой точки в старой системе координат равны 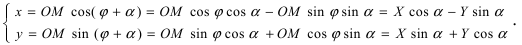 Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид
Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид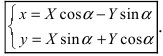 В матричном виде эти равенства можно записать в виде
В матричном виде эти равенства можно записать в виде 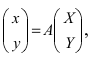 где матрица перехода
где матрица перехода 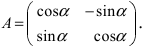
Найдем обратное преобразование системы координат, найдем матрицу 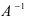 обратную к матрице А:
обратную к матрице А: 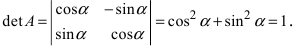
Найдем алгебраические дополнения всех элементов
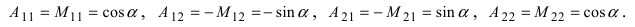 Запишем обратную матрицу
Запишем обратную матрицу 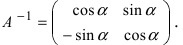
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.
Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.
Таким образом, имеем 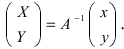 Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:
Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:
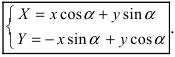
Пример:
Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол 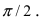
Решение:
Воспользуемся полученными формулами 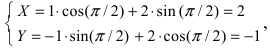 т.е. в новой системе координат точка имеет координаты М(2; -1).
т.е. в новой системе координат точка имеет координаты М(2; -1).
Рассмотрим применение преобразования координат:
а) Преобразовать уравнение параболы 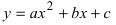 к каноническому виду. Проведем параллельный перенос системы координат
к каноническому виду. Проведем параллельный перенос системы координат 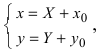 получим
получим 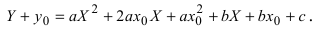 Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства
Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства 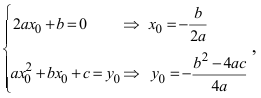 тогда уравнение принимает вид
тогда уравнение принимает вид 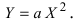 Выполним поворот системы координат на угол
Выполним поворот системы координат на угол 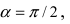 тогда
тогда 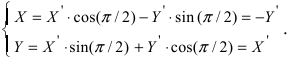 Подставим найденные соотношения в уравнение параболы
Подставим найденные соотношения в уравнение параболы 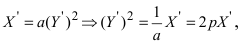 где параметр параболы
где параметр параболы 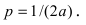
Пример:
Преобразовать уравнение параболы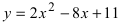 к каноническому виду.
к каноническому виду.
Решение:
Найдем начало отсчета новой системы координат после параллельного переноса 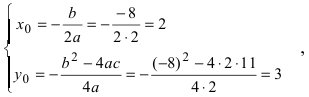 т.е. точка
т.е. точка 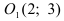 – начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид
– начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид 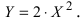 Проведем поворот системы отсчета на угол
Проведем поворот системы отсчета на угол 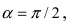 тогда
тогда
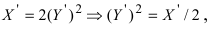 следовательно, параметр параболы р = 1/4.
следовательно, параметр параболы р = 1/4.
б) Выяснить, какую кривую описывает функция 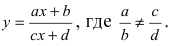
Проведем следующее преобразование 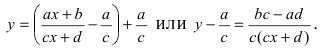 Производя параллельный перенос системы координат, вводя обозначение
Производя параллельный перенос системы координат, вводя обозначение
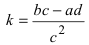 и новые координаты
и новые координаты 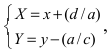 получим уравнение
получим уравнение 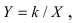 которое описывает равнобочную гиперболу.
которое описывает равнобочную гиперболу.
- Заказать решение задач по высшей математике
Полярные координаты. Замечательные кривые
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 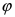 между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).
между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки). 
Рис. 48. Полярная система координат.
Главными значениями угла 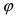 являются значения, лежащие в интервале
являются значения, лежащие в интервале 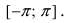 Из рисунка видно, что декартовы и полярные координаты связаны формулами
Из рисунка видно, что декартовы и полярные координаты связаны формулами 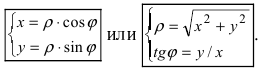
Рассмотрим замечательные кривые в полярной системе координат:
1. Спираль Архимеда 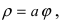 где число
где число 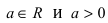 (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу
(Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу 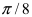 и на каждом луче отложим ему соответствующее значение р.
и на каждом луче отложим ему соответствующее значение р. 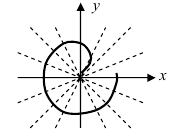
Рис. 49. Спираль (улитка) Архимеда.
2. Уравнение окружности: уравнение 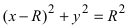 описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид
описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид 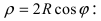
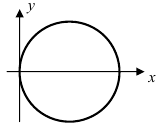
Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.
3. Уравнение 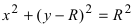 описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид
описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид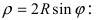
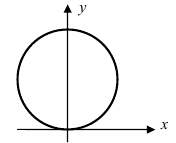
Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.
4. Кардиоиды: 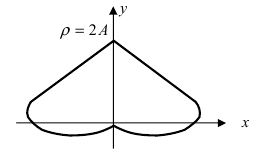
Рис. 52. Кардиоида 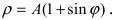
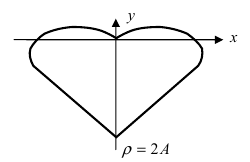
Рис. 53. Кардиоида 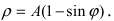
Аналогично выглядят кардиоиды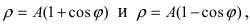 но они вытянуты вдоль оси абсцисс Ох.
но они вытянуты вдоль оси абсцисс Ох.
5. Петля: 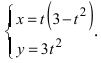 Величина
Величина 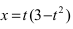 равна нулю при
равна нулю при 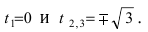
Для первого корня у = 0, а для второго и третьего – у = 9 . Следовательно, петля имеет вид 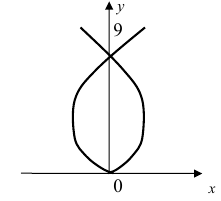
Рис. 54. Петля.
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
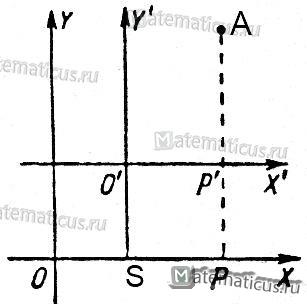
Формулы переноса начал координат равны:
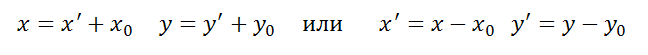
где
x,y — старые координаты точки;
x´, y´ — новые координаты точки;
x0, y0 — координаты нового начала в старой системе
Если обозначить
старые координаты точки A: х = ОР, у = РA;
новые координаты точки A: х’ = 0’Р’, у’ = Р’A;
координаты нового начала О’ в старой системе координат ХОY:
x0 = OS, y0 = SO’
то графически это можно представить следующим образом
Пример
Начало координат перенесено в точку (3;-4). Найти новые координаты точки L(-2;5)
Решение
x0=3, y0=-4, x=-2, y=5
Находим
x´=x-x0=-2-3=-5
y´=x-y0=5-(-4)=9
![]() 3376
3376
Макеты страниц
Обозначения (рис. 31):
— старые координаты точки 
— новые координаты точки 
— координаты нового начала О в старой системе 
Формулы переноса:

или

Словами: старая координата равна новой, сложенной с координатой нового начала (в старой системе).
Пример 1. Начало координат перенесено в точку (2; -5). Найти новые координаты точки 

Рис. 31
Решение. Имеем:

По формулам (2) находим:

Пример 2. Уравнение некоторой линии есть

Каково будет уравнение той же линии после переноса начала координат в точку 
Решение. Согласно формулам (1) имеем:

Подставим эти выражения в данное уравнение. Получим:

или после упрощений

Это — новое уравнение нашей линии. Из него видно, что эта линия есть окружность радиуса  с центром в точке О (§ 38).
с центром в точке О (§ 38).
3.8.1. Приведение уравнения центральной линии.
Метод инвариантов
Во-первых, термин. Инвариант – это величина, которая остаётся неизменной при тех или иных преобразованиях.
Простейший пример геометрического инварианта – это длина отрезка относительно его параллельного
переноса. В результате данного преобразовании меняются координаты концов отрезка, но его длина остаётся неизменной (инвариантной).
В частности, длина, ширина и толщина учебника Фихтенгольца (который можно положить на стол, на стул, на
кровать, под кровать, в мусорное ведро) – это инварианты относительно перемещения книги в пространстве. А вот если ненавистный томик порвать в
клочья, то его размеры уже перестанут быть инвариантами относительно этих механических повреждений. Но инвариантом останется сам математический
анализ. Так что рви, не рви, а осваивать его придётся 🙂
Однако вернёмся к нашему демонстрационному уравнению:
![]()
Очевидно, что можно выбрать бесконечно много других прямоугольных систем координат и получить бесконечно много различных уравнений вида ![]() , которые задают один и тот же эллипс.
, которые задают один и тот же эллипс.
И возникает вопрос: а есть ли у этого множества уравнений что-то одинаковое, характерное только для данной линии? Иными
словами, есть ли инварианты?
Да, есть!
Если линия второго порядка задана ![]() – общим уравнением в некоторой
– общим уравнением в некоторой
прямоугольной системе координат, то инвариантами относительно поворота и параллельного переноса прямоугольной системы координат являются следующие ЧИСЛА:
![]() – сумма коэффициентов при
– сумма коэффициентов при ![]() ,
,
старый знакомец ![]()
и ещё один определитель: 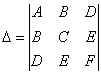 .
.
Рассмотрим исходное уравнение ![]() и поставим задачу
и поставим задачу
подобрать новую прямоугольную систему координат ![]() ТАК, чтобы
ТАК, чтобы
уравнение данной линии приняло в ней вид ![]() (который элементарно сводится к
(который элементарно сводится к
канонической форме). Заметим попутно логичную вещь – коэффициенты итогового уравнения, «отвечающие» за поворот и параллельный перенос равны нулю: ![]()
Поскольку инварианты (числа) ![]() НЕ ЗАВИСЯТ от коэффициентов
НЕ ЗАВИСЯТ от коэффициентов
того или иного уравнения, то справедливыми являются следующие равенства:
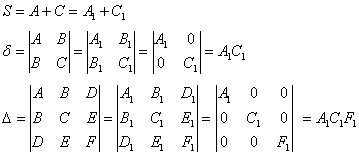
откуда следует простой и изящный алгоритм решения нашей задачи:
1) Из исходного уравнения находим числа 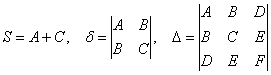 .
.
2) Решаем систему 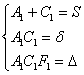 и записываем уравнение
и записываем уравнение ![]() , которое легко приводится к каноническому виду. При этом угол поворота новой системы
, которое легко приводится к каноническому виду. При этом угол поворота новой системы
координат ![]() относительно старой системы
относительно старой системы ![]() находится из уравнения
находится из уравнения ![]() . Если
. Если ![]() , то угол равен либо
, то угол равен либо ![]() , либо
, либо ![]() и это недостаток формулы. Но это не
и это недостаток формулы. Но это не
беда. Потому что есть другая формула: ![]() . Координаты нового начала координат
. Координаты нового начала координат ![]() отыскиваются как решение системы
отыскиваются как решение системы 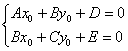 .
.
Таким образом, решение нашей задачи укладывается в стройную и понятную схему, доступную даже школьнику. Выясним же, наконец, как из потрёпанного
уравнения ![]() получается канонический эллипс
получается канонический эллипс ![]() :
:
Задача 111
Привести уравнение линии второго порядка к каноническому виду
![]()
Найти начало соответствующей системы координат и угол её поворота
Решение: перейдём к новой прямоугольной системе координат ![]() , в которой уравнение данной линии примет вид
, в которой уравнение данной линии примет вид ![]() .
.
На первом шаге из исходного уравнения находим коэффициенты ![]() . В тетради это удобно сделать следующим образом:
. В тетради это удобно сделать следующим образом:
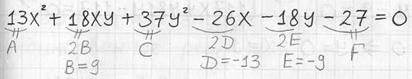
Здесь важно не потерять «минусы», а также не забыть разделить пополам нужные числа. Кроме того, некоторые слагаемые могут отсутствовать, и тогда соответствующие коэффициенты будут равны нулю – не спешим и не путаемся! В нашем
случае всё на месте и, соответственно, все коэффициенты ненулевые:
![]()
Вычислим инварианты:
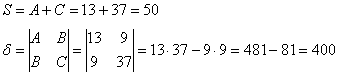
Последний определитель выгодно раскрыть с помощью элементарного преобразования, прибавив к
третьей строке первую строку:
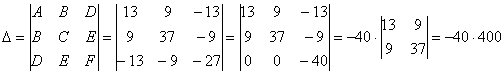
Инварианты найдены, составим и решим систему:
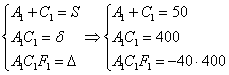
Из последних двух уравнений сразу просматривается значение коэффициента ![]() :
:
поскольку ![]() , то, подставляя это произведение в 3-е уравнение, получаем:
, то, подставляя это произведение в 3-е уравнение, получаем:
![]()
Но тут важнее разобраться с другими коэффициентами. Есть длинный путь, и есть короткий.
Путь длинный: из 1-го уравнения
выражаем ![]() – подставляем во второе уравнение:
– подставляем во второе уравнение:
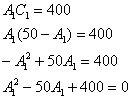
Решим квадратное уравнение:
![]()
В результате получается два комплекта симметричных корней:
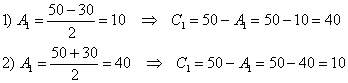
Путь короткий, к которому я рекомендую «пристреляться», в том числе, и «чайникам». Это подбор корней. Смотрим на первые два
уравнения системы: 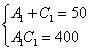 . Прикидку можно делать либо по первому уравнению, либо по
. Прикидку можно делать либо по первому уравнению, либо по
второму, кому как удобнее. Лично я привык ориентироваться по сумме коэффициентов. Правдоподобных вариантов здесь не так и много:
0 и 50
10 и 40 – удовлетворяет и первому и второму уравнению
20 и 30
30 и 20
40 и 10 – симметричная пара корней
50 и 0
Как видите, на подходящую пару чисел мы «натыкаемся» практически сразу. В силу симметричности уравнений решением будут являться и «зеркальные»
значения 40 и 10.
Таким образом, в нашем распоряжении оказывается два набора корней:
![]()
Не забываем выполнить проверку, подставив значения первого (можно второго) комплекта в левую часть каждого уравнения системы:
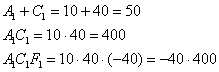
В результате получены соответствующие правые части исходных уравнений, что и требовалось проверить.
Теперь мысленно либо на черновике следует выяснить, какое решение приведёт нас к желаемому результату.
Подставляем первый комплект корней ![]() в уравнение
в уравнение ![]() :
:
![]()
Техника завершающих преобразований хорошо знакома:
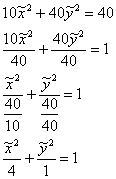
![]() – эллипс с центром в точке
– эллипс с центром в точке ![]() , большой полуосью
, большой полуосью ![]() , малой полуосью
, малой полуосью ![]() .
.
Такой фразы будет достаточно – нас никто не спрашивал про фокусы, эксцентриситет и другие характеристики линии.
Всё вышло удачно с первой попытки. Если в уравнение ![]() подставить второй
подставить второй
набор корней ![]() , то получится неканоническая запись того же эллипса
, то получится неканоническая запись того же эллипса ![]() – повёрнутого на 90 градусов.
– повёрнутого на 90 градусов.
Найдём угол поворота новой системы координат ![]() относительно старой:
относительно старой:
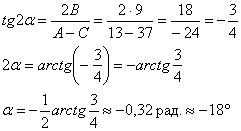
Или по второй, более лёгкой, но почему-то менее распространённой формуле:
![]()
Координаты ![]() начала новой системы координат
начала новой системы координат ![]() найдём как решение системы:
найдём как решение системы: 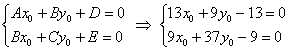
Первое уравнение умножим на 9, второе уравнение умножим на 13 и из 2-го уравнения почленно вычтем 1-е (проще способа не видно):
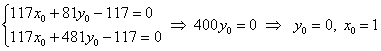 , таким образом:
, таким образом: ![]() .
.
В том случае если по условию необходимо выполнить чертёж – выполняем чертёж, приведённый выше. Впрочем, мне нетрудно скопировать:
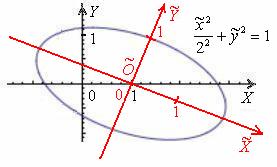 Ввиду сложности чертежа вполне допустимо его схематичное
Ввиду сложности чертежа вполне допустимо его схематичное
оформление, однако всё-таки постарайтесь, чтобы рисунок был похож на правду. Как вариант, можно изобразить только новую систему координат ![]() и эллипс в горизонтальном положении, но тогда прокомментируйте, что она
и эллипс в горизонтальном положении, но тогда прокомментируйте, что она
получена поворотом системы ![]() на угол
на угол ![]() и её параллельным переносом в точку
и её параллельным переносом в точку ![]() .
.
Ответ: ![]() – эллипс с полуосями
– эллипс с полуосями ![]() – в системе координат
– в системе координат ![]() с
с
началом в точке ![]() , повёрнутой относительно исходной системы координат
, повёрнутой относительно исходной системы координат ![]() на угол
на угол ![]() .
.
Это мы рассмотрели так называемый эллиптический случай, когда коэффициенты ![]() – отличны от нуля и одного знака (оба положительны либо оба отрицательны), т.е. когда их произведение
– отличны от нуля и одного знака (оба положительны либо оба отрицательны), т.е. когда их произведение ![]() .
.
И в этом случае может получиться не только эллипс. Если все три коэффициента ![]() одного знака, то это мнимый эллипс. Так, если бы в рассмотренной задаче
одного знака, то это мнимый эллипс. Так, если бы в рассмотренной задаче
мы получили уравнение ![]() , то пришли бы к уравнению
, то пришли бы к уравнению ![]() . Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа,
. Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа,
поскольку мнимый эллипс остаётся разве что мнить =)
Ещё одна разновидность эллиптического случая – нулевой свободный член: ![]() , предвестником которого является нулевой третий инвариант:
, предвестником которого является нулевой третий инвариант: ![]() . В частности, уравнение
. В частности, уравнение ![]() сводится к виду
сводится к виду ![]() – и это пара мнимых пересекающихся
– и это пара мнимых пересекающихся
прямых с единственной действительной точкой их пересечения ![]() (с нулевыми
(с нулевыми
координатами в новой системе координат ![]() ).
).
Предлагаю самостоятельно ознакомиться с гиперболическим случаем:
Задача 112
Привести уравнение линии второго порядка к каноническому виду
![]() , найти начало соответствующей системы координат, угол её поворота и
, найти начало соответствующей системы координат, угол её поворота и
выполнить чертёж.
После краткого образца решения есть важные дополнительные комментарии!
Теперь переходим к рассмотрению параболического случая ![]() , где по очевидной
, где по очевидной
причине метод инвариантов становится непригодным:
 3.8.2. Приведение уравнения нецентральной линии
3.8.2. Приведение уравнения нецентральной линии
 3.8. Приведение уравнения к каноническому виду
3.8. Приведение уравнения к каноническому виду
| Оглавление |
Автор: Aлeксaндр Eмeлин
преобразований координат, если начало координат
(без изменения направления осей) перенесено в
точку:
перенесено (без изменения направления осей) в
точку O’(3; -4). Координаты точек А(1; 3), B(-3; 0), C(-1; 4)
определены в новой системе. Вычислить координаты
этих же точек в старой системе координат.
3), C(-2; 5). Найти их координаты в новой системе, если
начало координат перенесено (без изменения
направления осей):
координаты начала O’ новой системы, если формулы
преобразования заданы следующими равенствами:
преобразований координат, если координатные оси
повернуты на один из следующих углов:
повернуты на угол
точек А(
в новой системе. Вычислить координаты этих же
точек в старой системе.
5), P(-3; -1). Найти их координаты в новой системе, если
оси координат повернуты на угол:
формулы преобразования координат заданы
следующими равенствами:
координаты точки O’ – нового начала координат,
если точка А(3; -4) лежит на новой оси абсцисс, а
точка B(2; 3) лежит на новой оси ординат, причем оси
старой и новой систем координат имеют
соответственно одинаковые направления.
преобразования координат, если точка M1(2; -3) лежит на новой
оси абсцисс, а точка M2(1; -7) лежит на новой оси ординат, причем
оси старой и новой систем координат имеют
соответственно одинаковые направления.
координатных осей Ox, Oy и Ox’, Oy’ имеют общее
начало О и преобразуются одна в дргую поворотом
на некоторый угол. Координаты точки А(3; –4)
определены относительно первой из них. Вывести
формулы преобразования координат, зная, что
положительное направление оси Ox’ определено
отрезком
перенесено в точку O’(-1; 2), координатные оси
повернуты на угол
2), M2(2; -3), M3(13; -13) определены
в новой системе. Вычислить координаты эти же
точек в старой системе координат.
139
-1), C(12; -6). Найти их координаты в новой системе,
если начало координат перенесено в точку В, а
координатные оси повернуты на угол
координаты нового начала и угол
который повернуты оси, если формулы
преобразвоания координат заданы следующими
равенствами:
координат перенесено в точку M1, а координатные оси повернуты так,
что положительное направление новой оси абсцисс
совпадает с направлением отрезка
формулы преобразования координат.
полярной системы координат параллельна оси
абсцисс декартовой прямоугольной системы и
направлена одинаково с нею. Даны декартовы
прямоугольные координаты полюса O(1; 2) и полярные
координаты точек M1(7;
–
координаты этих точек в декартовой
прямоугольной системе координат.
системы координат совпадает с началом
декартовых прямоугольных координат, а полярная
ось направлена по биссектрисе первого
координатного угла. Даны полярные координаты
точек M1(5;
M4(6; -3
–
ординаты этих точек.
полярной системы координат параллельна оси
абсцисс декартовой прямоугольной системы и
одинаково с нею направлена. Даны декартовы
прямоугольные координаты полюса O(3; 2) и точек M1(5; 2), M2(3; 1), M3(3; 5), M4(
координаты этих точек.
системы координат совпадает с началом
декартовых прямоугольных координат, полярная
ось направлена по биссектрисе первого
координатного угла. Даны декартовы координаты
точек M1(-1; 1), M2(
M5(
точек.