В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя – верхней части, и знаменателя – нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 1114, 1714, 914 имеют одинаковый знаменатель 14. Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 45 и 34 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 45 на 4, а числитель и знаменатель дроби 34 умножим на 5. Вместо дробей 45 и 34 получим соответственно 1620 и 1520.
Приведение дробей к общему знаменателю – это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменатель дробей – это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 16 и 35. Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5. Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Можно ди дроби 13, 216, 512 привести к общему знаменателю, который равен 150?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3, 6, 12. Другими словами, число 150 должно без остатка делиться на 3, 6, 12. Проверим:
150÷3=50, 150÷6=25, 150÷12=12,5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель дробей – это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел – это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
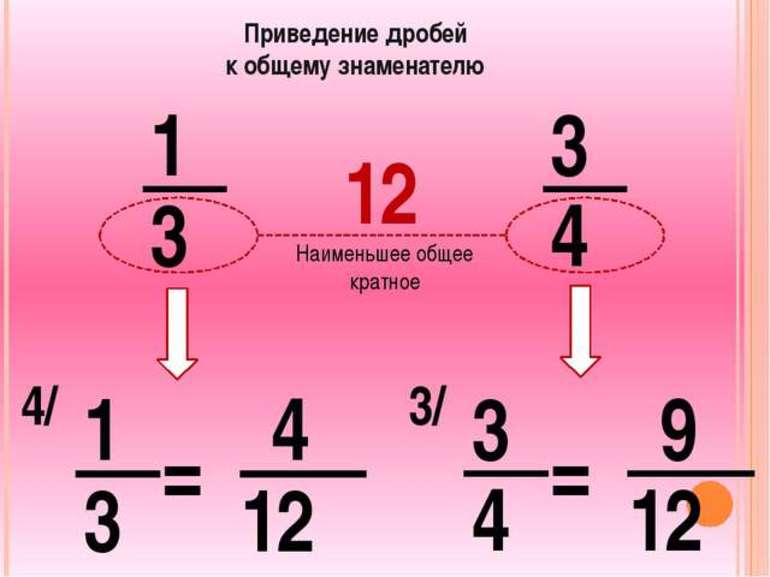
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Нужно найти наименьший общий знаменатель для дробей 110 и 12728.
Ищем НОК чисел 10 и 28. Разложим их на простые множители и получим:
10=2·528=2·2·7НОК(15, 28)=2·2·5·7=140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.
- Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Есть дроби 314 и 518. Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14=2·718=2·3·3НОК(14, 18)=2·3·3·7=126
Вычисляем дополнительные множители для каждой дроби. Для 314 дополнительный множитель находится как 126÷14=9, а для дроби 518 дополнительный множитель будет равен 126÷18=7.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3·914·9=27126, 5·718·7=35126.
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Привести дроби 32, 56,38 и 1718 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
НОК(2, 6)=6НОК(6, 8)=24НОК(24, 18)=72НОК(2, 6, 8, 18)=72
Далее вычислим дополнительные множители для каждой дроби.
Для 32 дополнительный множитель равен 72÷2= 36, для 56 дополнительный множитель равен 72÷6= 12, для 38 дополнительный множитель равен 72÷8= 9, наконец, для 1718 дополнительный множитель равен 72÷18= 4.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
32·36=1087256·12=607238·9=27721718·4=6872
Как привести дробь к наименьшему общему знаменателю (пример)

![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.
Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.
Формула основного свойства рациональных чисел.
Основное свойство рациональных чисел гласит:
(frac{p}{q}=frac{p times n}{q times n})
Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.
Рассмотрим пример:
(frac{1}{2}=frac{1 times 4}{2 times 4}=frac{4}{8})
Получаем,
(frac{1}{2}=frac{4}{8})
Наименьший общий знаменатель.
Что такое наименьший общий знаменатель?
Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.
Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:
Приведите дроби с разными знаменателями к наименьшему общему знаменателю .
Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.
У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2
Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2
НОК(14,20)= 2⋅5⋅2⋅7=140
Ответ: наименьший общий знаменатель будет равен 140.
Как привести дробь к общему знаменателю?
Нужно первую дробь (frac{1}{20}) домножить на 7, чтобы получить знаменатель 140.
(frac{1}{20}=frac{1 times 7}{20 times 7}=frac{7}{140})
А вторую дробь умножить на 10.
(frac{3}{14}=frac{3 times 10}{14 times 10}=frac{30}{140})
Правила или алгоритм приведения дробей к общему знаменателю.
Алгоритм приведения дробей к наименьшему общему знаменателю:
- Нужно разложить на простые множители знаменатели дробей.
- Нужно найти наименьшее общее кратное (НОК) для знаменателей данных дробей.
- Привести дроби к общему знаменателю, то есть умножить и числитель и знаменатель дроби на множитель.
Общий знаменатель для нескольких дробей.
Как найти общий знаменатель для нескольких дробей?
Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей (frac{2}{11}, frac{1}{15}, frac{3}{22})
Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.
Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2
Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330
Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби (frac{2}{11}, frac{1}{15}, frac{3}{22}) к общему знаменатели равному 330.
(begin{align}
frac{2}{11}=frac{2 times 30}{11 times 30}=frac{60}{330} \\
frac{1}{15}=frac{1 times 22}{15 times 22}=frac{22}{330} \\
frac{3}{22}=frac{3 times 15}{22 times 15}=frac{60}{330} \\
end{align})
Вопросы по теме:
Какой общий знаменатель у дробей (bf frac{2}{25}) и (bf frac{1}{14})?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.
Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.
Это мы нашли наименьший общий знаменатель:
( begin{align}
frac{2}{25}=frac{2 times 14}{25 times 14}=frac{28}{350} \\
frac{1}{14}=frac{1 times 25}{14 times 25}=frac{25}{350} \\
end{align})
Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей (frac{2}{25}) и (frac{1}{14}) знаменателем может быть число 700, 1400 и т.д.

Общий знаменатель
Самый простой способ, как привести дробь к общему знаменателю, — верхнюю и нижнюю части первой дроби умножить на значение в знаменателе второй, а верхнюю и нижнюю часть второго дробного числа — на значение в знаменателе первой. Проверочное правило, действующее в этом случае: дробь не меняется, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Даны две дроби: 3/13 и 3/7. После выполнения необходимых действий получится: 3/13*7 = 21/91, 3/7*13 =39/91.
Общий знаменатель (ОЗ) — это любое натуральное число, которое является всеобщим кратным всех данных дробей. Иными словами, это значит, что ОЗ может быть любое число из натуральных, которое обязательно будет делиться на знаменатель каждого дробного числа. Допустим, есть две обычных дробных соотношения 4/8 и 5/10. ОЗ в этом случае может быть любым значением, кратным 8 и 10. А конкретно, это значения: 80, 160, 240, 320, 400 и так далее.
Дано 3 дробных значения: 1/5, 3/10 и 9/15. Вопрос: может ли ОЗ быть числом 330? Ответ: да, потому что оно делится на знаменатель каждого соотношения без остатка: 330/5 = 66, 330/10 = 33, 330/15 = 22.
НОЗ и НОК
При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.
Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.
Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:
16=8*2; 6= 3*2
НОК (16, 6) =8*2*3= 48.
Число 48 и есть искомый НОЗ.

Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:
- Найти НОК.
- Для каждого дробного числа из ряда определить дополнительный множитель. Определить его можно с помощью деления НОЗ на знаменатель каждой из дробей.
- Умножить обе части каждой дроби на их дополнительные множители.
Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:
- Найти НОК: 14 = 2*7; 30 = 5*2*3; НОК (14,32) = 5*2*7*3 = 210;
- Найти дополнительные множители: 210/14 = 15; 210/30 = 7;
- Перемножить верхнюю и нижнюю части с дополнительными множителями: 3*15/14*15 = 45/210; 18*7/30*7 = 126/210.
Примеры с несколькими дробями
Правило поиска ОЗ и НОЗ действует также и в отношении нескольких дробных чисел в ряде. Есть три значения: 3/9, 8/11 и 10/12. Для того чтобы переводить их, нужно совершать те же действия, которые представлены в правиле:
НОК (9; 11) = 99; НОК (99; 12) = 39; НОК (9; 11; 12) = 396;
396/9 = 44; 396/11 = 36; 396/12 = 33;
3*44/9*44 = 132/396; 8*36/11*36 =288/396; 10*33/12*33 =330/396;
НОЗ найден.
Приводить дробные соотношения к ОЗ требуется во многих случаях. Вычисление этой величины необходимо, чтобы получить разность дробей, провести их сложение, умножение или деление, а также при решении задач на доли и проценты, так как процентные соотношения — это обыкновенные выражения, которые содержат дробные соотношения.
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Как приводить дроби к общему знаменателю
Если у обыкновенных дробей одинаковые знаменатели, то говорят, что эти дроби приведены к общему знаменателю.
Пример 1
Например, дроби $frac{3}{18}$ и $frac{20}{18}$ имеют одинаковые знаменатели. Говорят, что они имеют общий знаменатель $18$. Дроби $frac{1}{29}$, $frac{7}{29}$ и $frac{100}{29}$ имеют также одинаковые знаменатели. Говорят, что они имеют общий знаменатель $29$.
Если у дробей знаменатели не одинаковые, то их можно свести к общему знаменателю. Для этого необходимо умножить их числители и знаменатели на определенные дополнительные множители.
Пример 2
Как привести две дроби $frac{6}{11}$ и $frac{2}{7}$ к общему знаменателю.
Решение.
Умножим дроби $frac{6}{11}$ и $frac{2}{7}$ на дополнительные множители $7$ и $11$ соответственно и приведем их к общему знаменателю $77$:
$frac{6cdot 7}{11cdot 7}=frac{42}{77}$
$frac{2cdot 11}{7cdot 11}=frac{22}{77}$
Таким образом, приведением дробей к общему знаменателю называют умножение числителя и знаменателя данных дробей на дополнительные множители, которые в результате позволяют получить дроби с одинаковыми знаменателями.
Общий знаменатель
Определение 1
Любое положительное общее кратное всех знаменателей некоторого набора дробей называют общим знаменателем.
Другими словами, общий знаменатель заданных обыкновенных дробей – любое натуральное число, которое можно разделить на все знаменатели заданных дробей.
Из определения вытекает бесконечное множество общих знаменателей данного набора дробей.
Пример 3
Найти общие знаменатели дробей $frac{3}{7}$ и $frac{2}{13}$.
Решение.
Данные дроби имеют знаменатели, равные $7$ и $13$ соответственно. Положительные общие кратные чисел $2$ и $5$ равны $91, 182, 273, 364$ и т.д.
Любое из этих чисел можно использовать в качестве общего знаменателя дробей $frac{3}{7}$ и $frac{2}{13}$.
«Приведение дробей к общему знаменателю» 👇
Пример 4
Определить, можно ли дроби $frac{1}{2}$, $frac{16}{7}$ и $frac{11}{9}$ привести к общему знаменателю $252$.
Решение.
Чтобы определить, как привести дробь к общему знаменателю $252$, необходимо проверить является ли число $252$ общим кратным знаменателей $2, 7$ и $9$. Для этого разделим число $252$ на каждый из знаменателей:
$frac{252}{2}=126,$
$frac{252}{7}=36$,
$frac{252}{9}=28$.
Число $252$ делится нацело на все знаменатели, т.е. является общим кратным чисел $2, 7$ и $9$. Значит, данные дроби $frac{1}{2}$, $frac{16}{7}$ и $frac{11}{9}$ можно свести к общему знаменателю $252$.
Ответ: можно.
Наименьший общий знаменатель
Определение 2
Среди всех общих знаменателей заданных дробей можно выделить наименьшее натуральное число, которое называют наименьшим общим знаменателем.
Т.к. НОК – наименьший положительный общий делитель данного набора чисел, то НОК знаменателей заданных дробей является наименьшим общим знаменателем данных дробей.
Следовательно, чтобы найти наименьший общий знаменатель дробей, нужно найти НОК знаменателей этих дробей.
Пример 5
Заданы дроби $frac{4}{15}$ и $frac{37}{18}$. Найти их наименьший общий знаменатель.
Решение.
Знаменатели данных дробей равны $15$ и $18$. Найдем наименьший общий знаменатель как НОК чисел $15$ и $18$. Используем для этого разложение чисел на простые множители:
$15=3cdot 5$, $18=2cdot 3cdot 3$
$НОК(15, 18)=2cdot 3cdot 3cdot 5=90$.
Ответ: $90$.
Правило приведения дробей к наименьшему общему знаменателю
Чаще всего при решении задач алгебры, геометрии, физики и т.п. принято обыкновенные дроби приводить к наименьшему общему знаменателю, а не к любому общему знаменателю.
Алгоритм:
- С помощью НОК знаменателей заданных дробей найти наименьший общий знаменатель.
- 2.Вычислить дополнительный множитель для заданных дробей. Для этого найденный наименьший общий знаменатель необходимо разделить на знаменатель каждой дроби. Полученное число и будет дополнительным множителем данной дроби.
- Умножить на найденный дополнительный множитель числитель и знаменатель каждой дроби.
Пример 6
Найти наименьший общий знаменатель дробей $frac{4}{16}$ и $frac{3}{22}$ и привести к нему обе дроби.
Решение.
Воспользуемся алгоритмом приведения дробей к наименьшему общему знаменателю.
-
Вычислим наименьшее общее кратное чисел $16$ и $22$:
Разложим знаменатели на простые множители: $16=2cdot 2cdot 2cdot 2$, $22=2cdot 11$.
$НОК(16, 22)=2cdot 2cdot 2cdot 2cdot 11=176$.
-
Вычислим дополнительные множители для каждой дроби:
$176div 16=11$ – для дроби $frac{4}{16}$;
$176div 22=8$ – для дроби $frac{3}{22}$.
-
Умножим числители и знаменатели дробей $frac{4}{16}$ и $frac{3}{22}$ на дополнительные множители $11$ и $8$ соответственно. Получим:
$frac{4}{16}=frac{4cdot 11}{16cdot 11}=frac{44}{176}$
$frac{3}{22}=frac{3cdot 8}{22cdot 8}=frac{24}{176}$
Обе дроби приведены к наименьшему общему знаменателю $176$.
Ответ: $frac{4}{16}=frac{44}{176}$, $frac{3}{22}=frac{24}{176}$.
Иногда для того, чтобы находить наименьший общий знаменатель, нужно провести ряд трудоемких вычислений, что может не оправдывать цель решения задачи. В таком случае можно воспользоваться наиболее простым способ – свести дроби к общему знаменателю, который представляет собой произведение знаменателей данных дробей.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Как известно, обыкновенная дробь состоит из числителя и знаменателя. Знаменатель — это натуральное число находящееся под чертой:
a — числитель, b — знаменатель.
Общий знаменатель
Общий знаменатель — это любое натуральное число, которое без остатка делится на все знаменатели дробей, т.е. является их общим кратным. Для нескольких дробей можно найти бесконечно много общих знаменателей.
Пример 1: найти общий знаменатель для дробей
1 2
и
1 3
Для нахождения общего знаменателя достаточно найти числа кратные и двойке и тройке. Это будет: 6, 12, 18 и т.д. К примеру, 4, 8, 10 кратны двойке, но не кратны тройке — поэтому не будут являться общим знаменателем.
Наименьший общий знаменатель дробей
Зная, что такое общий знаменатель, нетрудно догадаться, что наименьший общий знаменатель — это наименьшее число, которое делится без остатка на все знаменатели дробей.
Возвращаясь к предыдущему примеру, можно с уверенностью сказать, что 12 будет общим знаменателем двойки и тройки, но наименьшим не будет. Наименьшим общим знаменателем будет — 6.
Таким образом: наименьший общий знаменатель двух дробей:
1 2
и
1 3
— является 6.
Как найти наименьший общий знаменатель?
Бывают ситуации когда в уме найти наименьший общий знаменатель сложно. Для этого есть алгоритм, который сводится к нахождению наименьшего общего кратного (НОК). НОК и будет являться НОЗ. Для нахождения НОК необходимо:
- разложить оба знаменателя на простые множители;
- выписать множители входящее в одно из разложений и добавить отсутствующие множители из второго разложения;
- вычислить их произведение.
Пример 2: Найти НОК чисел 12 и 8.
Согласно алгоритму раскладываем оба числа на простые множители:
Берем множители из первого разложения — 2, 2, 3. И добавляем отсутствующие из второго. В нашем случае во втором 3 двойки, но т.к. в первом разложении уже присутствуют 2 двойки — то недостающей будет одна. Таким образом получается набор цифр 2, 2, 3, 2 — которые необходимо перемножить. Отсюда 2 · 2 · 3 · 2 = 24.
Ответ: НОК (12; 8) = 24.
Пример 3: Найти НОК чисел 388 и 142.
Данный пример, с точки зрения вычислений сложнее, однако наглядно демонстрирует важность понимания алгоритма:
Аналогично, берем множители из первого разложения — 2, 2, 97. И добавляем отсутствующие из второго — 71. Отсюда 2 · 2 · 97 · 71 = 27548.
Ответ: НОК (388; 142) = 27548.
Практическое применение
На практике нахождение наименьшего общего знаменателя, используется, к примеру, при арифметических действиях с дробями (сложение, вычитание), при сравнении дробей и других задачах, где необходимо, как найти НОЗ, так и привести дроби к общему знаменателю.
Приведение дробей к общему знаменателю
Правило приведения дробей к общему знаменателю:
- Найти наименьший общий знаменатель дробей (НОЗ);
- Для каждой дроби найти дополнительный множитель (НОЗ разделить на каждый знаменатель);
- Умножаем числитель на дополнительный множитель.
Пример 4: привести дроби
4 12
и
3 8
к наименьшему общему знаменателю.
- Согласно алгоритму находим НОЗ для знаменателей 12 и 8. Выше, во втором примере, мы уже находили НОК для 12 и 8. Как уже было сказано ранее НОЗ = НОК. Таким образом, НОЗ = 24.
- Находим дополнительные множители:
24 : 12 = 2
24 : 8 = 3
- Умножаем числители на дополнительные множители:
4 · 2 = 8
3 · 3 = 9
Таким образом:
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Оцените материал:
![]() Загрузка…
Загрузка…
