Как найти нуль пространство матрицы

Ядро линейного отображения — это такое линейное подпространство области определения отображения, каждый элемент которого отображается в нулевой вектор ^[1][2]. А именно: если задано линейное отображение между двумя векторными пространствами V и W, то ядро отображения L — это векторное пространство всех элементов пространства V, таких что , где обозначает нулевой вектор из W^[3], или более формально:

Свойства[править | править код]

Ядро отображения L — это линейное подпространство области определения V^[4].
В линейном отображении два элемента V имеют один и тот же образ в W тогда и только тогда, когда их разность лежит в ядре отображения L:

Из этого следует, что образ L изоморфен факторпространству пространства V по ядру:

В случае, когда V конечномерно, из этого следует теорема о ранге и дефекте^[en]:

где под рангом мы понимаем размерность образа отображения L, а под дефектом — размерность ядра отображения L^[5].

Если V является предгильбертовым пространством, факторпространство можно отождествить с ортогональным дополнением к V пространства . Это является обобщением линейных операторов пространства строк или кообраза матрицы.

Приложение к модулям[править | править код]

Понятие ядра также имеет смысл для гомоморфизмов модулей, которые являются обобщениями векторных пространств, где скаляры — элементы кольца, а не поля. Область определения отображения — это модуль с ядром, образующий подмодуль. Здесь концепции ранга и размерности ядра не обязательны.

В функциональном анализе[править | править код]

Если и являются топологическими векторными пространствами, а конечномерно, то линейный оператор непрерывен тогда и только тогда, когда ядро отображения является замкнутым подпространством пространства .

Представление в виде матричного умножения[править | править код]

Рассмотрим линейное отображение, представленное матрицей размера с коэффициентами из поля (обычно из или ), то есть оперирующие с вектор-столбцами с элементами из поля .
Ядро этого линейного отображения — это множество решений уравнения , где понимается как нулевой вектор. Размерность ядра матрицы называется дефектом матрицы . В виде операций на множествах,

Матричное уравнение эквивалентно однородной системе линейных уравнений:

Тогда ядро матрицы — это то же самое, что и решение набора приведённых выше однородных уравнений.

Свойства подпространства[править | править код]

Ядро матрицы над полем является линейным подпространством . То есть ядро матрицы , множество , имеет следующие три свойства:

1. всегда содержит нулевой вектор, поскольку .
2. Если и , то . Это следует из свойства дистрибутивности матричного умножения.
3. Если , а является скаляром , то , поскольку .

Пространство строк матрицы[править | править код]

Произведение может быть записано в терминах скалярного произведения векторов следующим образом:

Здесь означают строки матрицы . Отсюда следует, что принадлежит ядру матрицы тогда и только тогда, когда вектор ортогонален (перпендикулярен) каждой из вектор-строк матрицы (поскольку ортогональность определяется как равенство нулю скалярного произведения).

Пространство строк, или кообраз матрицы , — это линейная оболочка вектор-строк матрицы . По указанным выше причинам ядро матрицы является ортогональным дополнением пространству строк. То есть вектор лежит в ядре матрицы тогда и только тогда, когда он перпендикулярен любому вектору из пространства строк матрицы .

Размерность пространства строк матрицы называется рангом матрицы , а размерность ядра матрицы называется дефектом матрицы . Эти величины связаны теоремой о ранге и дефекте^[en]

^[5]

Левое нуль-пространство (коядро)[править | править код]

Левое нуль-пространство или коядро матрицы состоит из всех векторов , таких что , где обозначает транспонирование матрицы. Левое нуль-пространство матрицы — это то же самое, что и ядро матрицы . Левое нуль-пространство матрицы является ортогональным дополнением пространству столбцов матрицы и двойственно коядру связанного линейного преобразования. Ядро, пространство строк, пространство столбцов
и левое нуль-пространство матрицы являются четырьмя фундаментальными подпространствами, ассоциированными с матрицей .

Неоднородные системы линейных уравнений[править | править код]

Ядро играет также большую роль при решении неоднородных систем линейных уравнений:

Пусть векторы и являются решениями уравнения выше, тогда

Таким образом, разность любых двух решений системы лежит в ядре матрицы .

Отсюда следует, что любое решение уравнения может быть выражено как сумма фиксированного решения и какого-либо элемента ядра. То есть множеством решений уравнения является

Геометрически это означает, что множество решений уравнения образовано параллельным переносом ядра матрицы на вектор . См. также Альтернатива Фредгольма.

Иллюстрация[править | править код]

Ниже приведена простая иллюстрация вычисления ядра матрицы (см. Вычисление методом Гаусса ниже для метода, более подходящего для более сложных вычислений). Иллюстрация затрагивает также пространства строк и их связь с ядром.

Рассмотрим матрицу

Ядро этой матрицы состоит из всех векторов , для которых

что можно выразить в виде однородной системы линейных уравнений относительно , и :

Те же самые равенства можно выписать в матричном виде:

С помощью метода Гаусса матрица может быть сведена к:

Преобразование матрицы в уравнения даёт:

Элементы ядра можно выразить в параметрическом виде следующим образом:

Поскольку является свободной переменной^[en], пробегающей по всем вещественным числам, это выражение можно эквивалентно переписать в виде:

Ядро матрицы — это в точности множество решений этих уравнений (в этом случае прямая через начало координат в ). Здесь вектор (−1,−26,16)^T образует базис ядра матрицы . Дефект матрицы равен 1.

Следующие скалярные произведения равны нулю:

что показывает, что вектора ядра матрицы ортогональны каждой вектор-строке матрицы .

Линейная оболочка этих двух (линейно независимых) вектор-строк — это плоскость, ортогональная вектору .

Поскольку ранг матрицы равен 2, размерность ядра матрицы равна 1, а размерность матрицы равна 3, мы имеем иллюстрацию теоремы о ранге и дефекте.

Примеры[править | править код]

,

то ядром оператора L является множество решений системы

Тогда ядро of L состоит из всех функций , для которых.

Тогда ядро of D состоит из всех функций в , производная которых равна нулю, то есть из всех постоянных функций.

Тогда ядром оператора s будет одномерное подпространство, состоящее из всех векторов .

Вычисления по методу Гаусса[править | править код]

Базис ядра матрицы можно вычислить с помощью метода Гаусса.

Для этой цели, если дана матрица , мы строим сначала расширенную^[en] по строкам матрицу , где — это единичная матрица.

Если вычислим ступенчатый по столбцам вид матрицы методом Гаусса (или любым другим подходящим методом), мы получим матрицу Базис ядра матрицы состоит из ненулевых столбцов матрицы , таких что соответствующие столбцы матрицы a нулевые.

Фактически вычисление может быть остановлено, как только матрица принимает ступенчатый по столбцам вид — остальное вычисление состоит из изменения базиса векторного пространства, образованного столбцами, верхняя часть которых равна нулю.

Например, представим, что

Тогда

Если привести верхнюю часть с помощью операций над столбцами к ступенчатому виду, получим

Последние три столбца матрицы нулевые. Поэтому три последних вектора матрицы ,

являются базисом ядра матрицы .

Доказательство, что метод вычисляет ядро: поскольку операции над столбцами соответствуют умножению справа на обратимую матрицу, из факта, что сводится к вытекает, что существует обратимая матрица , такая что где имеет ступенчатый вид. Тогда и Вектор-столбец принадлежит ядру матрицы (то есть ) тогда и только тогда, когда где Так как имеет ступенчатый вид, тогда и только тогда, когда ненулевые элементы соответствуют нулевым столбцам матрицы После умножения на можно сделать вывод, что это случается тогда и только тогда, когда является линейной комбинацией соответствующих столбцов матрицы

Численные вычисления[править | править код]

Задача вычисления ядра на компьютере зависит от природы коэффициентов.

Точные коэффициенты[править | править код]

Если коэффициенты матрицы заданы как точные числа, ступенчатый вид матрицы может быть вычислен алгоритмом Барейса, который более эффективен, чем метод Гаусса. Ещё более эффективно использование сравнения по модулю и китайской теоремы об остатках, которые сводят задачу к нескольким аналогичным задачам над конечными полями (что сокращает издержки, порождённые нелинейной вычислительной сложностью целочисленного умножения).

Для коэффициентов из конечного поля метод Гаусса работает хорошо, но для больших матриц, которые случаются в криптографии и при вычислении базиса Грёбнера, известны более эффективные алгоритмы, которые имеют почти ту же вычислительную сложность, но работают быстрее и более подходят для современных компьютерных устройств.

Вычисления с плавающей точкой[править | править код]

Для матриц, элементами которых служат числа с плавающей запятой, задача вычисления ядра имеет смысл только для матриц, число строк которых равно её рангу — ввиду ошибок округления^[en] матрицы с плавающими значениями почти всегда имеют полный ранг, даже когда они являются аппроксимацией матрицы много меньшего ранга. Даже для матрицы полного ранга можно вычислить её ядро только тогда, когда она хорошо обусловлена, то есть имеет низкое число обусловленности^[6].

И для хорошо обусловленной матрицы полного ранга метод Гаусса не ведёт себя корректно: ошибки округления слишком велики для получения значимого результата. Так как вычисление ядра матрицы является специальным случаем решения однородной системы линейных уравнений, ядро может быть вычислено любым алгоритмом, предназначенным для решения однородных систем. Передовым программным обеспечением для этих целей является библиотека Lapack.

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

• Hazewinkel, Michiel, ed. (2001), Kernel of a matrix, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Khan Academy, Introduction to the Null Space of a Matrix

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Ирвинг Капланский

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов 

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

.

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

След 

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали: 

След обладает следующими свойствами:

• Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

• Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.

• Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

• Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

• Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Заметим, что ‖x‖₂²=xᵀx.

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

1. Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

2. f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

3. Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

4. Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

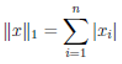
и норма l∞

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг 

Множество векторов {x₁, x₂, …, xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство

для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, …, xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

• Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

• Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

• Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

• Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).

Ортогональные матрицы 

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.

Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

Область значений и нуль-пространство матрицы

Линейной оболочкой множества векторов {x₁, x₂, …, xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, …, xₙ}, то есть

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

 Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы 

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Заметим, что

• Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

  

  (или просто A > 0), а множество всех положительно определенных матриц часто обозначают

  

  .

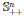
• Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

  

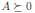
  (или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

  

  .

• Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

  

• , если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.

• Далее, симметричная матрица A ∈ 𝕊ⁿ называется отрицательно полуопределенной (

  

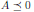
  ), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

• Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

  

  и

  

  .

Собственные значения и собственные векторы 

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

---

Перевод статьи был подготовлен в преддверии старта курса “Математика для Data Science”. Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

• ЗАПИСАТЬСЯ НА ДЕМОУРОК

Соседние файлы в папке scilab_manual

• #
• #
• #
• #
• #
• #
• #

Нулевое пространство

Сначала посмотрите на определение. A – это матрица размера m × n, а x – вектор-столбец. Если существует набор векторов N, выполняйте следующие условия:

 

Говорит, что N является нулевым пространством A.

Значение нулевого пространства

Из определения видно, что пустое пространство – это множество всех решений уравнения Ax = 0:

 

Нулевое пространство A связано с решением уравнения Ax = 0, а точнее, с пространством, образованным решением.Уравнение, равное нулевому вектору, также является значением «нуля» в нулевом пространстве. Поскольку x ∈ Rn, нулевое пространство также связано с решением x, поэтому пространство, образованное x, также находится в Rn, то является ли оно подпространством Rn?

Во-первых, вектор 0 – это набор решений уравнения. Предполагая, что v1 и v2 также являются решениями уравнения, теперь давайте посмотрим на завершение добавления:

V1, v2 удовлетворяют аддитивному замыканию. Наконец, проверьте замыкание умножения, C – произвольная константа:

 

V также удовлетворяет замкнутости умножения, поэтому нулевое пространство также является подпространством Rn. Поскольку нулевое пространство является подпространством, это подпространство должно включать нулевой вектор.Когда Ax = b, b ≠ 0, поскольку нет решения с нулевым значением, A не должно иметь нулевого пространства.

Найдите нулевое пространство

Мы уже знаем значение нулевого пространства, как найти нулевое пространство?

Сначала посмотрите на пример:

Пример относительно прост. Помимо всех нулевых решений, существует несколько наборов решений системы уравнений. В частности, если C – любая константа, то:

 

В пространстве R3 N (A) – прямая линия, проходящая через начало координат.

Вот еще один немного более сложный пример:

Нужно только решить систему уравнений, один из способов – преобразовать A в простейшую ступенчатую матрицу:

 

Чтобы облегчить решение, наша цель – сделать систему уравнений как можно меньше, чтобы мы могли еще больше упростить:

 

Преобразуйте простейшую ступенчатую матрицу строки в систему уравнений:

 

Два уравнения, четыре неизвестных, система уравнений имеет бесчисленное множество решений, является ли нулевое пространство A целым R4 или другими подпространствами R4? Прежде чем ответить на этот вопрос, нам необходимо дополнительно преобразовать уравнения:

 

X3, x4 могут быть любыми действительными числами, a и b линейно независимы, поэтому нулевое пространство A – это пространство, образованное a и b:

 

В частности, нулевое пространство A – это плоскость, проходящая через начало координат в пространстве R4, и, конечно же, это также подпространство в R4.

Нулевое пространство не имеет ничего общего с линейностью

Обратим внимание на природу A в Ax = 0. Am × n состоит из n векторов-столбцов:

 

Если A линейно независима, это означает, что система уравнений имеет только одно полностью нулевое решение, или, другими словами, множество решений этого уравнения является нулевым пространством A, и это нулевое пространство содержит только нулевые векторы. На этом этапе A должно быть упрощено до единичной матрицы:

 

Вывод состоит в том, что если и только если вектор-столбец A является линейно независимым, нулевое пространство A является нулевым вектором. В это время A должна быть квадратной матрицей, а простейшая ступенчатая матрица строк A является единичной матрицей. .

Колонка

Если A – матрица размера m × n, то пространство столбцов матрицы A – это пространство, образованное всеми векторами-столбцами в A. Пространство столбцов A представлено C (A):

C (A), очевидно, является подпространством в Rm.

Значение пространства столбца

Сначала вызовите матрицу:

 

Три вектора не могут образовывать все пространство R4, они могут образовывать только подпространство R4. Так в чем же смысл пространства столбцов? По-прежнему необходимо объединить уравнения.Нулевое пространство связано с решением Ax = 0; пространство столбцов связано с тем, в Ax = b, какой тип b может заставить уравнение иметь решение. Для любого b уравнение не всегда имеет решение, например следующее:

 

Четыре уравнения, три неизвестных, система уравнений может не иметь решения. С точки зрения векторного пространства три вектора не могут заполнить все четырехмерное пространство, поэтому должно быть много b, которые не являются линейными комбинациями этих трех векторов. В то же время эта система уравнений может быть разрешимой.Какой тип b может сделать систему уравнений разрешимой? Простой способ – сначала написать x, а затем вычесть b согласно b = Ax:

 

Можно видеть, что b является линейной комбинацией A, поэтому b должен находиться в пространстве столбцов A, а Ax = b имеет решение; и наоборот, если b не находится в пространстве столбцов A, это означает, что Ax = b не имеет решения, которое имеет значение.

В приведенном выше примере третий вектор-столбец A может быть представлен линейной комбинацией первых двух, поэтому пространство столбцов A является двумерным подпространством R4:

пример

Что такое подпространства в R3?

 

Сначала посмотрите на подпространство. Подпространство включает в себя нулевые векторы. Линейная комбинация всех векторов в подпространстве все еще находится в подпространстве.

1. Здесь описывается, что взаимосвязь между компонентами вектора является линейной, что может быть преобразовано в уравнение:

 

<A1, a2, a3> – это пустое пространство <1,1, -1>, а пустое пространство – это подпространство R3.

2. Три компонента больше не являются линейными, что означает, что 80% не является подпространством, и вы можете перечислить несколько векторов по желанию. Когда a1 = 1, a2 = 1, a3 = a1 a2 = 1, <a1, a2, a3> = <1, 1, 1>, поскольку подпространство закрыто для логарифмического умножения, поэтому <2, 2, 2> будет также Оно должно быть в подпространстве, но в это время a3 ≠ a1a2, поэтому условие вопроса 2 не может составлять подпространство.

3. Сначала упростите выражение:

 

<A1, a2, a3> – это линейная комбинация <1, 0, -1> и <1, 0, 1>, которая является подпространством.

4. Давайте сначала упростим выражение:

 

Обратите внимание, что второй компонент равен 1. Это фиксированное значение, которое не может образовывать нулевой вектор.Условие вопроса 4 не может образовывать подпространство.

---

Автор: Я 8-битный

Источник:http://www.cnblogs.com/bigmonkey

Эта статья посвящена изучению, исследованию и распространению информации. Если вам нужно перепечатать, свяжитесь со мной и укажите автора и источник. Она не предназначена для коммерческого использования! Чтобы

Отсканируйте QR-код, чтобы подписаться на общедоступную учетную запись «Я 8-значный»