Как найти нулевой икс в квадратном уравнении - Сайт, где вы сможете решить свои вопросы

Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.

Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.

Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х 2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).

Пример №1. Решить уравнение:

Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х 2 =45; найдем переменную в квадрате, поделив обе части уравнения на 5: х 2 =9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:

Ответ: х=±3 или можно записать ответ так: х₁=–3, х₂=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:

Выполним решение уже известным способом: –6х 2 =90. х 2 =–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:

Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х₁=10, х₂=–10.

Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.

Пример №4. Решить уравнение:

Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.

Пример №5. Решить уравнение:

Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.

Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.

Пример №6. Решить уравнение:

Обе части уравнения делим на (–14) и получаем х 2 =0, откуда соответственно и единственный корень – нуль. Пример №6. Решить уравнение:

Также делим обе части на 23 и получаем х 2 =0. Значит, корень уравнения – нуль.

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три формулы неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;
ax² + bx = 0, при c = 0.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −5x² = 0.

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = – c,
разделим обе части на a: x² = – c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение – c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если – c/а 0, то корни уравнения x² = – c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = – c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = – c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

не имеет корней при – c/а 0.

Пример 1. Найти решение уравнения 9x² + 4 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 9:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на -1:

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

Пример 1. Решить уравнение 2x² – 32x = 0

Вынести х за скобки

Это уравнение равносильно х = 0 и 2x – 32 = 0.

Решить линейное уравнение:

Значит корни исходного уравнения — 0 и 16.

Ответ: х = 0 и х = 16.

Пример 2. Решить уравнение 3x² – 12x = 0

Разложить левую часть уравнения на множители и найти корни:

Квадратное уравнение

Что такое квадратное уравнение и как его решать?

Мы помним, что уравнение это равенство, содержащее в себе переменную, значение которой нужно найти.

Если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение называют уравнением второй степени или квадратным уравнением.

Например, следующие уравнения являются квадратными:

Решим первое из этих уравнений, а именно x 2 − 4 = 0 .

Все тождественные преобразования, которые мы применяли при решении обычных линейных уравнений, можно применять и при решении квадратных.

Итак, в уравнении x 2 − 4 = 0 перенесем член −4 из левой части в правую часть, изменив знак:

Получили уравнение x 2 = 4 . Ранее мы говорили, что уравнение считается решённым, если в одной части переменная записана в первой степени и её коэффициент равен единице, а другая часть равна какому-нибудь числу. То есть чтобы решить уравнение, его следует привести к виду x = a , где a — корень уравнения.

У нас переменная x всё ещё во второй степени, поэтому решение необходимо продолжить.

Чтобы решить уравнение x 2 = 4 , нужно ответить на вопрос при каком значении x левая часть станет равна 4 . Очевидно, что при значениях 2 и −2 . Чтобы вывести эти значения воспользуемся определением квадратного корня.

Число b называется квадратным корнем из числа a , если b 2 = a и обозначается как

У нас сейчас похожая ситуация. Ведь, что такое x 2 = 4 ? Переменная x в данном случае это квадратный корень из числа 4, поскольку вторая степень x прирáвнена к 4.

Тогда можно записать, что . Вычисление правой части позвóлит узнать чему равно x . Квадратный корень имеет два значения: положительное и отрицательное. Тогда получаем x = 2 и x = −2 .

Обычно записывают так: перед квадратным корнем ставят знак «плюс-минус», затем находят арифметическое значение квадратного корня. В нашем случае на этапе когда записано выражение , перед следует поставить знак ±

Затем найти арифметическое значение квадратного корня

Выражение x = ± 2 означает, что x = 2 и x = −2 . То есть корнями уравнения x 2 − 4 = 0 являются числа 2 и −2 . Запишем полностью решение данного уравнения:

Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:

В обоих случаях левая часть равна нулю. Значит уравнение решено верно.

Решим ещё одно уравнение. Пусть требуется решить квадратное уравнение (x + 2) 2 = 25

Для начала проанализируем данное уравнение. Левая часть возведенá в квадрат и она равна 25 . Какое число в квадрате равно 25 ? Очевидно, что числа 5 и −5

То есть наша задача найти x, при которых выражение x + 2 будет равно числам 5 и −5 . Запишем эти два уравнения:

Решим оба уравнения. Это обычные линейные уравнения, которые решаются легко:

Значит корнями уравнения (x + 2) 2 = 25 являются числа 3 и −7 .

В данном примере как и в прошлом можно использовать определение квадратного корня. Так, в уравнения (x + 2) 2 = 25 выражение (x + 2) представляет собой квадратный корень из числа 25 . Поэтому можно cначала записать, что .

Тогда правая часть станет равна ±5 . Полýчится два уравнения: x + 2 = 5 и x + 2 = −5. Решив по отдельности каждое из этих уравнений мы придём к корням 3 и −7 .

Запишем полностью решение уравнения (x + 2) 2 = 25

Из рассмотренных примеров видно, что квадратное уравнение имеет два корня. Чтобы не забыть о найденных корнях, переменную x можно подписывать нижними индексами. Так, корень 3 можно обозначить через x₁ , а корень −7 через x₂

В предыдущем примере тоже можно было сделать так. Уравнение x 2 − 4 = 0 имело корни 2 и −2 . Эти корни можно было обозначить как x₁ = 2 и x₂ = −2.

Бывает и так, что квадратное уравнение имеет только один корень или вовсе не имеет корней. Такие уравнения мы рассмотрим позже.

Сделаем проверку для уравнения (x + 2) 2 = 25 . Подставим в него корни 3 и −7 . Если при значениях 3 и −7 левая часть равна 25 , то это будет означать, что уравнение решено верно:

В обоих случаях левая часть равна 25 . Значит уравнение решено верно.

Квадратное уравнение бывает дано в разном виде. Наиболее его распространенная форма выглядит так:

ax 2 + bx + c = 0 ,
где a, b, c — некоторые числа, x — неизвестное.

Это так называемый общий вид квадратного уравнения. В таком уравнении все члены собраны в общем месте (в одной части), а другая часть равна нулю. По другому такой вид уравнения называют нормальным видом квадратного уравнения.

Пусть дано уравнение 3x 2 + 2x = 16 . В нём переменная x возведенá во вторую степень, значит уравнение является квадратным. Приведём данное уравнение к общему виду.

Итак, нам нужно получить уравнение, которое будет похоже на уравнение ax 2 + bx + c = 0 . Для этого в уравнении 3x 2 + 2x = 16 перенесем 16 из правой части в левую часть, изменив знак:

Получили уравнение 3x 2 + 2x − 16 = 0 . В этом уравнении a = 3 , b = 2 , c = −16 .

В квадратном уравнении вида ax 2 + bx + c = 0 числа a , b и c имеют собственные названия. Так, число a называют первым или старшим коэффициентом; число b называют вторым коэффициентом; число c называют свободным членом.

В нашем случае для уравнения 3x 2 + 2x − 16 = 0 первым или старшим коэффициентом является 3 ; вторым коэффициентом является число 2 ; свободным членом является число −16 . Есть ещё другое общее название для чисел a, b и c — параметры.

Так, в уравнении 3x 2 + 2x − 16 = 0 параметрами являются числа 3 , 2 и −16 .

В квадратном уравнении желательно упорядочивать члены так, чтобы они располагались в таком же порядке как у нормального вида квадратного уравнения.

Например, если дано уравнение −5 + 4x 2 + x = 0 , то его желательно записать в нормальном виде, то есть в виде ax 2 + bx + c = 0.

В уравнении −5 + 4x 2 + x = 0 видно, что свободным членом является −5 , он должен располагаться в конце левой части. Член 4x 2 содержит старший коэффициент, он должен располагаться первым. Член x соответственно будет располагаться вторым:

Квадратное уравнение в зависимости от случая может принимать различный вид. Всё зависит от того, чему равны значения a , b и с .

Если коэффициенты a , b и c не равны нулю, то квадратное уравнение называют полным. Например, полным является квадратное уравнение 2x 2 + 6x − 8 = 0 .

Если какой-то из коэффициентов равен нулю (то есть отсутствует), то уравнение значительно уменьшается и принимает более простой вид. Такое квадратное уравнение называют неполным. Например, неполным является квадратное уравнение 2x 2 + 6x = 0, в нём имеются коэффициенты a и b (числа 2 и 6 ), но отсутствует свободный член c.

Рассмотрим каждый из этих видов уравнений, и для каждого из этих видов определим свой способ решения.

Пусть дано квадратное уравнение 2x 2 + 6x − 8 = 0 . В этом уравнении a = 2 , b = 6 , c = −8 . Если b сделать равным нулю, то уравнение примет вид:

Получилось уравнение 2x 2 − 8 = 0 . Чтобы его решить перенесем −8 в правую часть, изменив знак:

Для дальнейшего упрощения уравнения воспользуемся ранее изученными тождественными преобразованиями. В данном случае можно разделить обе части на 2

У нас получилось уравнение, которое мы решали в начале данного урока. Чтобы решить уравнение x 2 = 4 , следует воспользоваться определением квадратного корня. Если x 2 = 4 , то . Отсюда x = 2 и x = −2 .

Значит корнями уравнения 2x 2 − 8 = 0 являются числа 2 и −2 . Запишем полностью решение данного уравнения:

В обоих случаях левая часть равна нулю, значит уравнение решено верно.

Уравнение, которое мы сейчас решили, является неполным квадратным уравнением. Название говорит само за себя. Если полное квадратное уравнение выглядит как ax 2 + bx + c = 0 , то сделав коэффициент b нулём получится неполное квадратное уравнение ax 2 + c = 0 .

У нас тоже сначала было полное квадратное уравнение 2x 2 + 6x − 4 = 0 . Но мы сделали коэффициент b нулем, то есть вместо числа 6 поставили 0 . В результате уравнение обратилось в неполное квадратное уравнение 2x 2 − 4 = 0 .

В начале данного урока мы решили квадратное уравнение x 2 − 4 = 0 . Оно тоже является уравнением вида ax 2 + c = 0 , то есть неполным. В нем a = 1 , b = 0 , с = −4 .

Также, неполным будет квадратное уравнение, если коэффициент c равен нулю.

Рассмотрим полное квадратное уравнение 2x 2 + 6x − 4 = 0 . Сделаем коэффициент c нулём. То есть вместо числа 4 поставим 0

Получили квадратное уравнение 2x 2 + 6x=0 , которое является неполным. Чтобы решить такое уравнение, переменную x выносят за скобки:

Получилось уравнение x(2x + 6) = 0 в котором нужно найти x, при котором левая часть станет равна нулю. Заметим, что в этом уравнении выражения x и (2x + 6) являются сомножителями. Одно из свойств умножения говорит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).

В нашем случае равенство будет достигаться, если x будет равно нулю или (2x + 6) будет равно нулю. Так и запишем для начала:

Получилось два уравнения: x = 0 и 2x + 6 = 0 . Первое уравнение решать не нужно — оно уже решено. То есть первый корень равен нулю.

Чтобы найти второй корень, решим уравнение 2x + 6 = 0 . Это обычное линейное уравнение, которое решается легко:

Видим, что второй корень равен −3.

Значит корнями уравнения 2x 2 + 6x = 0 являются числа 0 и −3 . Запишем полностью решение данного уравнения:

Выполним проверку. Подставим корни 0 и −3 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 0 и −3 левая часть равна нулю, то это будет означать, что уравнение решено верно:

Следующий случай это когда числа b и с равны нулю. Рассмотрим полное квадратное уравнение 2x 2 + 6x − 4 = 0 . Сделаем коэффициенты b и c нулями. Тогда уравнение примет вид:

Получили уравнение 2x 2 = 0 . Левая часть является произведением, а правая часть равна нулю. Произведение равно нулю, если хотя бы один из сомножителей равен нулю. Очевидно, что x = 0 . Действительно, 2 × 0 2 = 0 . Отсюда, 0 = 0 . При других значениях x равенства достигаться не будет.

Проще говоря, если в квадратном уравнении вида ax 2 + bx + c = 0 числа b и с равны нулю, то корень такого уравнения равен нулю.

Отметим, что когда употребляются словосочетания « b равно нулю » или « с равно нулю «, то подразумевается, что параметры b или c вовсе отсутствуют в уравнении.

Например, если дано уравнение 2x 2 − 32 = 0 , то мы говорим, что b = 0 . Потому что если сравнить с полным уравнением ax 2 + bx + c = 0 , то можно заметить, что в уравнении 2x 2 − 32 = 0 присутствует старший коэффициент a , равный 2; присутствует свободный член −32 ; но отсутствует коэффициент b .

Наконец, рассмотрим полное квадратное уравнение ax 2 + bx + c = 0 . В качестве примера решим квадратное уравнение x 2 − 2x + 1 = 0 .

Итак, требуется найти x , при котором левая часть станет равна нулю. Воспользуемся изученными ранее тождественными преобразованиями.

Прежде всего заметим, что левая часть уравнения представляет собой квадрат разности двух выражений. Если мы вспомним как раскладывать многочлен на множители, то получим в левой части (x − 1) 2 .

Рассуждаем дальше. Левая часть возведенá в квадрат и она равна нулю. Какое число в квадрате равно нулю? Очевидно, что только 0 . Поэтому наша задача найти x , при котором выражение x − 1 равно нулю. Решив простейшее уравнение x − 1 = 0 , можно узнать чему равно x

Этот же результат можно получить, если воспользоваться квадратным корнем. В уравнении (x − 1) 2 = 0 выражение (x − 1) представляет собой квадратный корень из нуля. Тогда можно записать, что . В этом примере записывать перед корнем знак ± не нужно, поскольку корень из нуля имеет только одно значение — ноль. Тогда получается x − 1 = 0 . Отсюда x = 1 .

Значит корнем уравнения x 2 − 2x + 1 = 0 является единица. Других корней у данного уравнения нет. В данном случае мы решили квадратное уравнение, имеющее только один корень. Такое тоже бывает.

Не всегда бывают даны простые уравнения. Рассмотрим например уравнение x 2 + 2x − 3 = 0 .

В данном случае левая часть уже не является квадратом суммы или разности. Поэтому нужно искать другие пути решения.

Заметим, что левая часть уравнения представляет собой квадратный трехчлен. Тогда можно попробовать выделить полный квадрат из этого трёхчлена и посмотреть что это нам даст.

Выделим полный квадрат из квадратного трёхчлена, располагающего в левой части уравнения:

В получившемся уравнении перенесем −4 в правую часть, изменив знак:

Теперь воспользуемся квадратным корнем. В уравнении (x + 1) 2 = 4 выражение (x + 1) представляет собой квадратный корень из числа 4 . Тогда можно записать, что . Вычисление правой части даст выражение x + 1 = ±2 . Отсюда полýчится два уравнения: x + 1 = 2 и x + 1 = −2 , корнями которых являются числа 1 и −3

Значит корнями уравнения x 2 + 2x − 3 = 0 являются числа 1 и −3 .

Пример 3. Решить уравнение x 2 − 6x + 9 = 0 , выделив полный квадрат.

Выделим полный квадрат из левой части:

Далее воспользуемся квадратным корнем и узнáем чему равно x

Значит корнем уравнения x 2 − 6x + 9 = 0 является 3. Выполним проверку:

Пример 4. Решить квадратное уравнение 4x 2 + 28x − 72 = 0 , выделив полный квадрат:

Выделим полный квадрат из левой части:

Перенесём −121 из левой части в правую часть, изменив знак:

Воспользуемся квадратным корнем:

Получили два простых уравнения: 2x + 7 = 11 и 2x + 7 = −11. Решим их:

Пример 5. Решить уравнение 2x 2 + 3x − 27 = 0

Это уравнение немного посложнее. Когда мы выделяем полный квадрат, первый член квадратного трёхчлена мы представляем в виде квадрата какого-нибудь выражения.

Так, в прошлом примере первым членом уравнения был 4x 2 . Его можно было представить в виде квадрата выражения 2x , то есть (2x) 2 = 2 2 x 2 = 4x 2 . Чтобы убедиться что это правильно, можно извлечь квадратный корень из выражения 4x 2 . Это квадратный корень из произведения — он равен произведению корней:

В уравнении 2x 2 + 3x − 27 = 0 первый член это 2x 2 . Его нельзя представить в виде квадрата какого-нибудь выражения. Потому что нет числá, квадрат которого равен 2. Если бы такое число было, то этим числом был бы квадратный корень из числа 2. Но квадратный корень из числа 2 извлекается только приближённо. А приближённое значение не годится для представления числá 2 в виде квадрата.

Если обе части исходного уравнения умножить или разделить на одно и то же число, то полýчится уравнение равносильное исходному. Это правило сохраняется и для квадратного уравнения.

Тогда можно разделить обе части нашего уравнения на 2 . Это позвóлит избавиться от двойки перед x 2 что впоследствии даст нам возможность выделить полный квадрат:

Перепишем левую часть в виде трёх дробей со знаменателем 2

Сократим первую дробь на 2. Остальные члены левой части перепишем без изменений. Правая часть по-прежнему станет равна нулю:

Выделим полный квадрат.

При представлении члена в виде удвоенного произведения, появление множителя 2 привело бы к тому, что этот множитель и знаменатель дроби сократились бы. Чтобы этого не произошло, удвоенное произведение было домножено на . При выделении полного квадрата всегда нужно стараться сделать так, чтобы значение изначального выражения не изменилось.

Свернём полученный полный квадрат:

Приведём подобные члены:

Перенесём дробь в правую часть, изменив знак:

Воспользуемся квадратным корнем. Выражение представляет собой квадратный корень из числа

Для вычисления правой части воспользуемся правилом извлечения квадратного корня из дроби:

Тогда наше уравнение примет вид:

Полýчим два уравнения:

Значит корнями уравнения 2x 2 + 3x − 27 = 0 являются числа 3 и .

Корень удобнее оставить в таком виде, не выполняя деления числителя на знаменатель. Так проще будет выполнять проверку.

Выполним проверку. Подставим найденные корни в исходное уравнение:

В обоих случаях левая часть равна нулю, значит уравнение 2x 2 + 3x − 27 = 0 решено верно.

Решая уравнение 2x 2 + 3x − 27 = 0 , в самом начале мы разделили обе его части на 2 . В результате получили квадратное уравнение, в котором коэффициент перед x 2 равен единице:

Такой вид квадратного уравнения называют приведённым квадратным уравнением.

Любое квадратное уравнение вида ax 2 + bx + c = 0 можно сделать приведённым. Для этого нужно разделить обе его части на коэффициент, который располагается перед x². В данном случае обе части уравнения ax 2 + bx + c = 0 нужно разделить на a

Пример 6. Решить квадратное уравнение 2x 2 + x + 2 = 0

Сделаем данное уравнение приведённым:

Выделим полный квадрат:

Получили уравнение , в котором квадрат выражения равен отрицательному числу . Такого быть не может, поскольку квадрат любого числа или выражения всегда положителен.

Следовательно, нет такого значения x , при котором левая часть стала бы равна . Значит уравнение не имеет корней.

А поскольку уравнение равносильно исходному уравнению 2x 2 + x + 2 = 0 , то и оно (исходное уравнение) не имеет корней.

Формулы корней квадратного уравнения

Выделять полный квадрат для каждого решаемого квадратного уравнения не очень удобно.

Можно ли создать универсальные формулы для решения квадратных уравнений? Оказывается можно. Сейчас мы этим и займёмся.

Взяв за основу буквенное уравнение ax 2 + bx + c = 0 , и выполнив некоторые тождественные преобразования, мы сможем получить формулы для вывода корней квадратного уравнения ax 2 + bx + c = 0 . В эти формулы можно будет подставлять коэффициенты a , b , с и получать готовые решения.

Итак, выделим полный квадрат из левой части уравнения ax 2 + bx + c = 0. Сначала сделаем данное уравнение приведённым. Разделим обе его части на a

Теперь в получившемся уравнении выделим полный квадрат:

Перенесем члены и в правую часть, изменив знак:

Приведём правую часть к общему знаменателю. Дроби, состоящие из букв, привóдят к общему знаменателю методом «крест-нáкрест». То есть знаменатель первой дроби станóвится дополнительным множителем второй дроби, а знаменатель второй дроби станóвится дополнительным множителем первой дроби:

В числителе правой части вынесем за скобки a

Сократим правую часть на a

Поскольку все преобразования были тождественными, то получившееся уравнение имеет те же корни, что и исходное уравнение ax 2 + bx + c = 0.

Уравнение будет иметь корни только тогда, если правая часть больше нуля или равна нулю. Это потому что в левой части выполнено возведéние в квадрат, а квадрат любого числа положителен или равен нулю (если в этот квадрат возвóдится ноль). А чему будет равна правая часть зависит от того, что будет подставлено вместо переменных a , b и c .

Поскольку при любом a не рáвным нулю, знаменатель правой части уравнения всегда будет положительным, то знак дроби будет зависеть от знака её числителя, то есть от выражения b 2 − 4ac .

Выражение b 2 − 4ac называют дискриминантом квадратного уравнения. Дискриминант это латинское слово, означающее различитель . Дискриминант квадратного уравнения обозначается через букву D

Дискриминант позволяет заранее узнать имеет ли уравнение корни или нет. Так, в предыдущем задании мы долго решали уравнение 2x 2 + x + 2 = 0 и оказалось, что оно не имеет корней. Дискриминант же позволил бы нам заранее узнать, что корней нет. В уравнении 2x 2 + x + 2 = 0 коэффициенты a , b и c равны 2, 1 и 2 соответственно. Подставим их в формулу D = b 2 −4ac

D = b 2 − 4ac = 1 2 − 4 × 2 × 2 = 1 − 16 = −15.

Видим, что D (оно же b 2 − 4ac ) является отрицательным числом. Тогда нет смысла решать уравнение 2x 2 + x + 2 = 0, выделяя в нём полный квадрат, потому что когда мы дойдем до уравнения вида , окажется что правая часть станет меньше нуля (из-за отрицательного дискриминанта). А квадрат числа не может быть отрицательным. Следовательно, корней у данного уравнения не будет.

Станóвится понятно почему древние люди считали выражение b 2 − 4ac различителем. Это выражение подобно индикатору позволяет различить уравнение имеющего корни от уравнения, не имеющего корней.

Итак, D равно b 2 − 4ac . Подставим в уравнении вместо выражения b 2 − 4ac букву D

Если дискриминант исходного уравнения окажется меньше нуля (D , то уравнение примет вид:

В этом случае говорят, что у исходного уравнения корней нет, поскольку квадрат любого числа не должен быть отрицательным.

Если дискриминант исходного уравнения окажется больше нуля (D > 0) , то уравнение примет вид:

В этом случае уравнение будет иметь два корня. Для их вывода воспользуемся квадратным корнем:

Получили уравнение . Из него полýчится два уравнения: и . Выразим x в каждом из уравнений:

Получившиеся два равенства это и есть универсальные формулы для решения квадратного уравнения ax 2 + bx + c = 0. Их называют формулами корней квадратного уравнения .

Чаще всего эти формулы обозначаются как x₁ и x₂ . То есть для вычисления первого корня используется формула c индексом 1; для вывода второго корня — формула с индексом 2. Обозначим свои формулы так же:

Очерёдность применения формул не важнá.

Решим например квадратное уравнение x 2 + 2x − 8 = 0 с помощью формул корней квадратного уравнения. Коэффициенты данного квадратного уравнения это числа 1 , 2 и −8 . То есть, a = 1 , b = 2 , c = −8 .

Прежде чем использовать формулы корней квадратного уравнения, нужно найти дискриминант этого уравнения.

Найдём дискриминант квадратного уравнения. Для этого воспользуемся формулой D = b 2 − 4 ac . Вместо переменных a, b и c у нас будут коэффициенты уравнения x 2 + 2x − 8 = 0

D = b 2 − 4ac = 2 2 − 4 × 1 × (−8) = 4 + 32 = 36

Дискриминант больше нуля. Значит уравнение имеет два корня. Теперь можно воспользоваться формулами корней квадратного уравнения:

Значит корнями уравнения x 2 + 2x − 8 = 0 являются числа 2 и −4 . Проверкой убеждаемся, что корни найдены верно:

Наконец, рассмотрим случай когда дискриминант квадратного уравнения равен нулю. Вернёмся к уравнению . Если дискриминант равен нулю, то правая часть уравнения примет вид:

И в этом случае квадратное уравнение будет иметь только один корень. Воспользуемся квадратным корнем:

Далее выражаем x

Это ещё одна формула для вывода корня квадратного корня. Рассмотрим её применение. Ранее мы решили уравнение x 2 − 6x + 9 = 0 , имеющее один корень 3. Решили мы его методом выделения полного квадрата. Теперь попробуем решить с помощью формул.

Найдём дискриминант квадратного уравнения. В этом уравнении a = 1 , b = −6 , c = 9 . Тогда по формуле дискриминанта имеем:

D = b 2 − 4ac = (−6) 2 − 4 × 1 × 9 = 36 − 36 = 0

Дискриминант равен нулю (D = 0) . Это означает, что уравнение имеет только один корень, и вычисляется он по формуле

Значит корнем уравнения x 2 − 6x + 9 = 0 является число 3.

Для квадратного уравнения, имеющего один корень также применимы формулы и . Но применение каждой из них будет давать один и тот же результат.

Применим эти две формулы для предыдущего уравнения. В обоих случаях получим один и тот же ответ 3

Если квадратное уравнение имеет только один корень, то желательно применять формулу , а не формулы и . Это позволяет сэкономить время и место.

Пример 3. Решить уравнение 5x 2 − 6x + 1 = 0

Найдём дискриминант квадратного уравнения:

Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:

Значит корнями уравнения 5x 2 − 6x + 1 = 0 являются числа 1 и .

Ответ: 1; .

Пример 4. Решить уравнение x 2 + 4x + 4 = 0

Найдём дискриминант квадратного уравнения:

Дискриминант равен нулю. Значит уравнение имеет только один корень. Он вычисляется по формуле

Значит корнем уравнения x 2 + 4x + 4 = 0 является число −2 .

Пример 5. Решить уравнение 3x 2 + 2x + 4 = 0

Найдём дискриминант квадратного уравнения:

Дискриминант меньше нуля. Значит корней у данного уравнения нет.

Ответ: корней нет.

Пример 6. Решить уравнение (x + 4) 2 = 3x + 40

Приведём данное уравнение к нормальному виду. В левой части располагается квадрата суммы двух выражений. Раскрóем его:

Перенесём все члены из правой части в левую часть, изменив их знаки. В правой части останется ноль:

Приведём подобные члены в левой части:

В получившемся уравнении найдём дискриминант:

Значит корнями уравнения (x + 4) 2 = 3x + 40 являются числа 3 и −8 .

Ответ: 3 ; −8.

Пример 7. Решить уравнение

Умнóжим обе части данного уравнения на 2 . Это позвóлит нам избавиться от дроби в левой части:

В получившемся уравнении перенесём 22 из правой части в левую часть, изменив знак. В правой части останется 0

Приведём подобные члены в левой части:

В получившемся уравнении найдём дискриминант:

Значит корнями уравнения являются числа 23 и −1 .

Ответ: 23; −1.

Пример 8. Решить уравнение

Умнóжим обе части на наименьшее общее кратное знаменателей обеих дробей. Это позвóлит избавиться от дробей в обеих частях. Наименьшее общее кратное чисел 2 и 3 это число 6 . Тогда получим:

В получившемся уравнении раскроем скобки в обеих частях:

Теперь перенесём все члены из правой части в левую часть, изменив у них знаки. В правой части останется 0

Приведём подобные члены в левой части:

В получившемся уравнении найдём дискриминант:

Значит корнями уравнения являются числа и 2.

Примеры решения квадратных уравнений

Пример 1. Решить уравнение x 2 = 81

Это простейшее квадратное уравнение, в котором надо определить число, квадрат которого равен 81. Таковыми являются числа 9 и −9. Воспользуемся квадратным корнем для их вывода:

Ответ: 9, −9 .

Пример 2. Решить уравнение x 2 − 9 = 0

Это неполное квадратное уравнение. Для его решения нужно перенести член −9 в правую часть, изменив знак. Тогда получим:

Ответ: 3, −3.

Пример 3. Решить уравнение x 2 − 9x = 0

Это неполное квадратное уравнение. Для его решения сначала нужно вынести x за скобки:

Левая часть уравнения является произведением. Произведение равно нулю, если хотя один из сомножителей равен нулю.

Левая часть станет равна нулю, если отдельно x равно нулю, или если выражение x − 9 равно нулю. Получится два уравнения, одно из которых уже решено:

Ответ: 0, 9 .

Пример 4. Решить уравнение x 2 + 4x − 5 = 0

Это полное квадратное уравнение. Его можно решить методом выделения полного квадрата или с помощью формул корней квадратного уравнения.

Решим данное уравнение с помощью формул. Сначала найдём дискриминант:

D = b 2 − 4ac = 4 2 − 4 × 1 × (−5) = 16 + 20 = 36

Дискриминант больше нуля. Значит уравнение имеет два корня. Вычислим их:

Ответ: 1, −5 .

Пример 5. Решить уравнение

Умнóжим обе части на наименьшее общее кратное чисел 5, 3 и 6. Это позвóлит избавиться от дробей в обеих частях:

В получившемся уравнении перенесём все члены из правой части в левую часть, изменив знак. В правой части останется ноль:

Приведём подобные члены:

Решим получившееся уравнение с помощью формул:

Ответ: 5 , .

Пример 6. Решить уравнение x 2 = 6

В данном примере как и в первом нужно воспользоваться квадратным корнем:

Однако, квадратный корень из числа 6 не извлекается. Он извлекается только приближённо. Корень можно извлечь с определённой точностью. Извлечём его с точностью до сотых:

Но чаще всего корень оставляют в виде радикала:

Ответ:

Пример 7. Решить уравнение (2x + 3) 2 + (x − 2) 2 = 13

Раскроем скобки в левой части уравнения:

В получившемся уравнении перенесём 13 из правой части в левую часть, изменив знак. Затем приведём подобные члены:

Получили неполное квадратное уравнение. Решим его:

Ответ: 0 , −1,6 .

Пример 8. Решить уравнение (5 + 7x)(4 − 3x) = 0

Данное уравнение можно решить двумя способами. Рассмотрим каждый из них.

Первый способ. Раскрыть скобки и получить нормальный вид квадратного уравнения.

Приведём подобные члены:

Перепишем получившееся уравнение так, чтобы член со старшим коэффициентом располагался первым, член со вторым коэффициентом — вторым, а свободный член располагался третьим:

Чтобы старший член стал положительным, умнóжим обе части уравнения на −1. Тогда все члены уравнения поменяют свои знаки на противоположные:

Решим получившееся уравнение с помощью формул корней квадратного уравнения:

Второй способ. Найти значения x , при которых сомножители левой части уравнения равны нулю. Этот способ удобнее и намного короче.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю. В данном случае равенство в уравнении (5 + 7x)(4 − 3x) = 0 будет достигаться, если выражение (5 + 7x) равно нулю, или же выражение (4 − 3x) равно нулю. Наша задача выяснить при каких x это происходит:

Примеры решения задач

Предстáвим, что возникла необходимость построить небольшую комнату, площадь которой 8 м 2 . При этом длина комнаты должна быть в два раза больше её ширины. Как определить длину и ширину такой комнаты?

Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:

Обозначим ширину комнаты через x . А длину комнаты через 2x , потому что по условию задачи длина должна быть в два раза больше ширины. Множитель 2 и выполнит это требование:

Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:

По условию задачи площадь должна быть 8 м 2 . Значит выражение 2x × x следует приравнять к 8

Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.

Первое что можно сделать это выполнить умножение в левой части уравнения:

В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.

Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2

Теперь воспользуемся квадратным корнем. Если x 2 = 4 , то . Отсюда x = 2 и x = −2 .

Через x была обозначена ширина комнаты. Ширина не должна быть отрицательной, поэтому в расчёт берём только значение 2 . Такое часто бывает при решении задачи, в которых применяется квадратное уравнение. В ответе получаются два корня, но условию задачи удовлетворяет только один из них.

А длина была обозначена через 2x . Значение x теперь известно, подставим его в выражение 2x и вычислим длину:

Значит длина равна 4 м , а ширина 2 м . Это решение удовлетворяет условию задачи, поскольку площадь комнаты равна 8 м 2

Ответ: длина комнаты составляет 4 м , а ширина 2 м .

Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м 2

Решение

Длина прямоугольника, как правило, больше его ширины. Пусть ширина участка x метров, а длина (x + 10) метров. Площадь участка составляет 1200 м 2 . Умножим длину участка на его ширину и приравняем к 1200 , получим уравнение:

Решим данное уравнение. Для начала раскроем скобки в левой части:

Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется 0

Решим получившееся уравнение с помощью формул:

Несмотря на то, что квадратное уравнение имеет два корня, в расчёт берём только значение 30 . Потому что ширина не может выражаться отрицательным числом.

Итак, через x была обозначена ширина участка. Она равна тридцати метрам. А длина была обозначена через выражение x + 10 . Подставим в него найденное значение x и вычислим длину:

x + 10 = 30 + 10 = 40 м

Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30 ) получится 1200 м 2

40 × 30 = 1200 м 2

Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно найти периметр участка.

Периметр прямоугольника это сумма всех его сторон. Тогда:

P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.

Ответ: длина изгороди огородного участка составляет 140 м.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/nepolnye-kvadratnye-uravneniya

Квадратное уравнение

[/spoiler]

Источник

Как найти икс нулевое

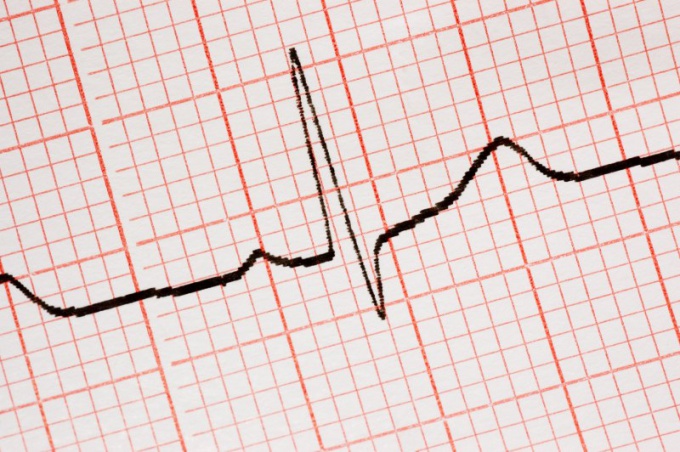
В качестве «икс нулевое» обозначается координата вершины параболы по оси абсцисс. В этой точке функция принимает наибольшее или наименьшее значение, поэтому x0 − точка экстремума функции.

Инструкция

Если имеется аналитическое задание функции, приведите ее к стандартному виду: A*x²+B*x+C=y(x), где A − старший коэффициент при x², B − средний коэффициент при x, C − свободный член. Обратите внимание, чтобы коэффициент при x² не равнялся нулю, иначе это будет уже не квадратичная функция.

Координата вершины параболы x0 по оси абсцисс находится по формуле: x0=-B/2A. В случае приведенного квадратного уравнения, то есть, когда A=1, формула упрощается: x0=-B/2. Если в уравнении нет «икса» в первой степени, значит, коэффициент B=0, и тогда x0 тоже обращается в нуль.

Чтобы найти координату вершины параболы по оси ординат, подставьте полученное значение для x0 в уравнение. Когда вы упростите выражение, с одной стороны у вас останется «игрек», с другой − некоторое число Q. Оно и показывает ординату вершины параболы: y0=Q.

Итак, исследование аналитически заданной функции дало вам точку на графике с координатами (x0;y0). Если старший коэффициент A > 0, то ветви параболы направлены вверх, и в вершине промежуток убывания будет сменяться промежутком возрастания. Если же A

Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.

Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D < 0, корней нет;
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

x² − 8x + 12 = 0;

5x² + 3x + 7 = 0;

x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

x² − 2x − 3 = 0;

15 − 2x − x² = 0;

x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

[x=frac{-12+sqrt{0}}{2cdot 1}=-6]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x² + 9x = 0;
x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

x² − 7x = 0;

5x² + 30 = 0;

4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

Теорема Виета
Следствия из теоремы Виета
Тест на тему «Значащая часть числа»
Метод коэффициентов, часть 1
Однородные тригонометрические уравнения: общая схема решения
Задача B4: строительные бригады

Источник

Квадра́тное уравне́ние — алгебраическое уравнение второй степени с общим видом

${displaystyle ax^{2}+bx+c=0,;aneq 0,}$

в котором — неизвестное, а коэффициенты , и — вещественные или комплексные числа.

Корень уравнения $ax^{2}+bx+c=0$ — это значение неизвестного , обращающее квадратный трёхчлен ${displaystyle ax^{2}+bx+c}$ в ноль, а квадратное уравнение в верное числовое равенство. Также это значение называется корнем самого многочлена ${displaystyle ax^{2}+bx+c.}$

Элементы квадратного уравнения имеют собственные названия^[1]:

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице^[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент :

${displaystyle x^{2}+px+q=0,quad p={dfrac {b}{a}},quad q={dfrac {c}{a}}.}$

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

Квадратное уравнение является разрешимым в радикалах, то есть его корни могут быть выражены через коэффициенты в общем виде.

Исторические сведения о квадратных уравнениях[править | править код]

Древний Вавилон[править | править код]

Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения^[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:

$x^{2}+x={frac {3}{4}}; x^{2}-x=14{frac {1}{2}}.$

Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.

Индия[править | править код]

Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)^[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: ${displaystyle ax^{2}+bx=c;}$ притом предполагалось, что в нём все коэффициенты, кроме могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.

Корни квадратного уравнения на множестве действительных чисел[править | править код]

I способ. Общая формула для вычисления корней с помощью дискриминанта[править | править код]

Дискриминантом квадратного уравнения ${displaystyle ax^{2}+bx+c=0}$ называется величина ${displaystyle {mathcal {D}}=b^{2}-4ac}$ .

Условие
Количество корней	Два корня	Один корень кратности 2 (другими словами, два равных корня)	Действительных корней нет
Формула	${displaystyle x_{1,2}={frac {-bpm {sqrt {mathcal {D}}}}{2a}}}$ (1)	${displaystyle x=-{frac {b}{2a}}}$	—

Данный метод универсальный, однако не единственный.

II способ. Корни квадратного уравнения при чётном коэффициенте b[править | править код]

Для уравнений вида $ax^{2}+2kx+c=0$ , то есть при чётном , где

$k={frac {1}{2}}b,$

вместо формулы (1) для нахождения корней существует возможность использования более простых выражений^[1].

Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b = 2k, через несложные преобразования.

Дискриминант	Корни
неприведённое	приведённое	D > 0	неприведённое	приведённое
удобнее вычислять значение четверти дискриминанта: ${frac {D}{4}}=k^{2}-ac$ Все необходимые свойства при этом сохраняются.	${frac {D}{4}}=k^{2}-c$ .	$x_{1,2}={frac {-kpm {sqrt {k^{2}-ac}}}{a}}.$	$x_{1,2}=-kpm {sqrt {k^{2}-c}}$
D = 0	$x={frac {-k}{a}}$

III способ. Решение неполных квадратных уравнений[править | править код]

К решению неполных квадратных уравнений практикуется особый подход. Рассматриваются три возможных ситуации.

IV способ. Использование частных соотношений коэффициентов[править | править код]

Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.

Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту[править | править код]

Если в квадратном уравнении $ax^{2}+bx+c=0$ сумма первого коэффициента и свободного члена равна второму коэффициенту: a+c=b , то его корнями являются и число, противоположное отношению свободного члена к старшему коэффициенту ( $-{frac {c}{a}}$ ).

Доказательство

Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):

${displaystyle {mathcal {D}}=b^{2}-4ac=(a+c)^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}}$

Да, это так, ведь при любых действительных значениях коэффициентов $(a-c)^{2}geqslant 0$ , а значит и дискриминант неотрицателен. Таким образом, если anot =c , то уравнение имеет два корня, если же a=c , то оно имеет только один корень.
Найдём эти корни:

${displaystyle x_{1,2}={frac {-bpm {sqrt {mathcal {D}}}}{2a}}={frac {-(a+c)pm {sqrt {(a-c)^{2}}}}{2a}}={frac {-a-cpm |a-c|}{2a}}={frac {-a-cpm amp c}{2a}}}$

$x_{1}={frac {-a-c-a+c}{2a}}={frac {-2a}{2a}}=-1;$

$x_{2}={frac {-a-c+a-c}{2a}}={frac {-2c}{2a}}=-{frac {c}{a}}.$

В частности, если a=c , то корень будет один: -1.

Способ 2.

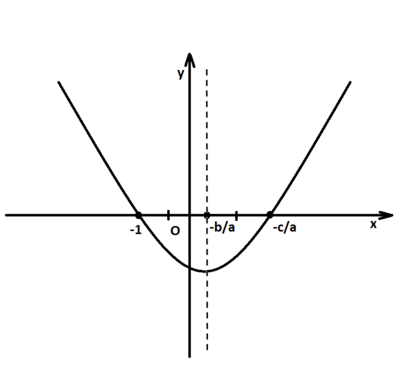
Геометрическая интерпретация: парабола, заданная аналитически указанной формулой, пересекает ось x в двух точках, абсциссами которых и являются корни, хотя бы один из которых равен -1

Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы $y=ax^{2}+bx+c$ с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой $x=-{frac {b}{2a}}$ . Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: $-{frac {b}{2a}}+rho (x_{1};-{frac {b}{2a}})=x_{2}$ (если $x_{1}<x_{2}$ ) или $-{frac {b}{2a}}-rho (-{frac {b}{2a}};x_{1})=x_{2}$ (если верно неравенство противоположного смысла). Используя тождество , выражающее геометрический смысл модуля, а также принимая, что $x_{1}=-1$ (это можно доказать, подставив равенство в квадратный трёхчлен: $acdot (-1)^{2}+bcdot (-1)+c=(a+c)-b=0$ , поэтому -1 – корень такого уравнения) , приходим к следующему равенству: $-{frac {b}{2a}}pm |-{frac {b}{2a}}-(-1)|=x_{2}.$ Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем – отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве b-a=c , раскрываем модуль: $x_{2}=-{frac {b}{2a}}-{frac {b}{2a}}+1=-{frac {2b-2a}{2a}}=-{frac {b-a}{a}}=-{frac {c}{a}}$ . Во втором случае,совершив аналогичные преобразования, придём к тому же результату, ч.т.д.

Отсюда следует, что перед решением какого-либо квадратного уравнения целесообразна проверка возможности применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.

Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю[править | править код]

Если в квадратном уравнении сумма всех его коэффициентов равна нулю ( a+b+c=0 ), то корнями такого уравнения являются и отношение свободного члена к старшему коэффициенту ( ${frac {c}{a}}$ ).

Доказательство

Способ 1. Прежде всего заметим, что из равенства a+b+c=0 следует, что
Установим количество корней:

${displaystyle {mathcal {D}}=b^{2}-4ac=(-(a+c))^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}.}$

При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов $(a-c)^{2}geqslant 0$ , а значит и дискриминант неотрицателен. Обратите внимание, что если anot =c , то уравнение имеет два корня, если же a=c , то только один.
Найдём эти корни:

${displaystyle x_{1,2}={frac {-bpm {sqrt {mathcal {D}}}}{2a}}={frac {a+cpm {sqrt {(a-c)^{2}}}}{2a}}={frac {a+cpm |a-c|}{2a}}={frac {a+cpm amp c}{2a}};}$

$x_{1}={frac {a+c+a-c}{2a}}={frac {2a}{2a}}=1;$

$x_{2}={frac {a+c-a+c}{2a}}={frac {2c}{2a}}={frac {c}{a}},$

что и требовалось доказать.

В частности, если a=c

, то уравнение имеет только один корень, которым является число

Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: $acdot 1^{2}+bcdot 1+c=0$ – верное равенство, следовательно, единица – корень такого вида квадратных уравнений. Далее, по теореме Виета находим второй корень: согласно этой теореме, произведение корней уравнения равно числу, равному отношению свободного члена к старшему коэффициенту – $x_{1}x_{2}={frac {c}{a}}Rightarrow x_{2}={frac {c}{ax_{1}}}={frac {c}{acdot 1}}={frac {c}{a}}$ , ч.т.д.

Отсюда следует, что перед решением уравнения стандартными методами целесообразна проверка применимости к нему этой теоремы, а именно сложение всех коэффициентов данного уравнения и установление, не равна ли нулю эта сумма.

V способ. Разложение квадратного трёхчлена на линейные множители[править | править код]

Если трёхчлен вида ${displaystyle ax^{2}+bx+c~(anot =0)}$ удастся каким-либо образом представить в качестве произведения линейных множителей , то можно найти корни уравнения $ax^{2}+bx+c=0$ — ими будут $-{frac {m}{k}}$ и $-{frac {n}{l}}$ , действительно, ведь ${displaystyle (kx+m)(lx+n)=0Longleftrightarrow {biggl [}{begin{array}{lcl}kx+m=0,\lx+n=0,end{array}}}$ а решив указанные линейные уравнения, получим вышеописанное. Квадратный трёхчлен не всегда раскладывается на линейные множители с действительными коэффициентами: это возможно, если соответствующее ему уравнение имеет действительные корни.

Рассматриваются некоторые частные случаи.

Использование формулы квадрата суммы (разности)[править | править код]

Если квадратный трёхчлен имеет вид $(ax)^{2}+2abx+b^{2}$ , то применив к нему названную формулу, можно разложить его на линейные множители и, значит, найти корни:

${displaystyle (ax)^{2}+2abx+b^{2}=(ax+b)^{2},}$

${displaystyle (ax+b)^{2}=0,}$

$x=-{frac {b}{a}}.$

Выделение полного квадрата суммы (разности)[править | править код]

Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:

прибавляют и отнимают одно и то же число:
$x^{2}+px+({frac {p}{2}})^{2}-({frac {p}{2}})^{2}+q=0;$ .
применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть:
${displaystyle (x^{2}+2{frac {p}{2}}x+({frac {p}{2}})^{2})+(-({frac {p}{2}})^{2}+q)=0,}$
$(x+{frac {p}{2}})^{2}={frac {p^{2}}{4}}-q;$
извлекают из левой и правой частей уравнения квадратный корень и выражают переменную:
${displaystyle x+{frac {p}{2}}=pm {sqrt {{frac {p^{2}}{4}}-q}},}$
$x_{1,2}=-{frac {p}{2}}pm {sqrt {{frac {p^{2}}{4}}-q}}.$

Примечание: данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a = 1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.

VI способ. Использование прямой и обратной теоремы Виета[править | править код]

Прямая теорема Виета (см. ниже) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к вычислениям по формуле (1).

Согласно обратной теореме, всякая пара чисел (число) $x_{1},x_{2}$ , будучи решением системы уравнений

${displaystyle {begin{cases}x_{1}+x_{2}=-p,\x_{1}x_{2}=q,end{cases}}}$

являются корнями уравнения $x^{2}+px+q=0$

Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:

1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;

2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.

VII способ. Метод «переброски»[править | править код]

По своей сущности метод «переброски» является просто модификацией теоремы Виета.

Метод «переброски» — это сведение уравнения, которое нельзя привести так, чтобы все коэффициенты остались целыми, к приведённому уравнению с целыми коэффициентами:

1) умножаем обе части на старший коэффициент:

${displaystyle ax^{2}+bx+c=0quad mid ;cdot a,}$

${displaystyle (ax)^{2}+b(ax)+ac=0;}$

2) заменяем

${displaystyle y^{2}+by+ac=0.}$

Далее решаем уравнение относительно y по методу, описанному выше, и находим x = y/a.

Как можно заметить, в методе «переброски» старший коэффициент как раз «перебрасывается» к свободному члену.

Графическое решение квадратного уравнения[править | править код]

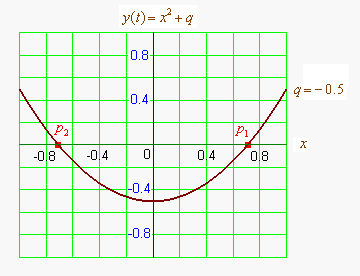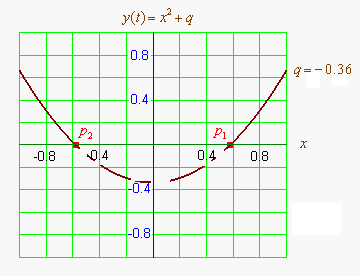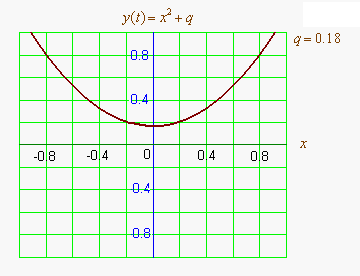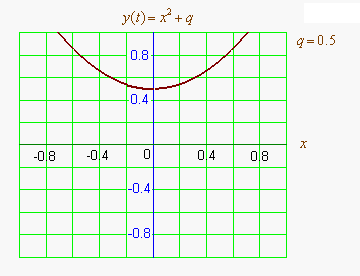
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)

Если коэффициент положительный, ветви параболы направлены вверх и наоборот. Если коэффициент положительный (при положительном , при отрицательном наоборот), то вершина параболы лежит в левой полуплоскости и наоборот.

Графический способ решения квадратных уравнений[править | править код]

Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида заключается в следующем: в одной системе координат строят графики функций y=f(x) и y=g(x) и находят абсциссы общих точек этих графиков; найденные числа и будут корнями уравнения.

Есть всего пять основных способов графического решения квадратных уравнений.

Приём I[править | править код]

Для решения квадратного уравнения $ax^{2}+bx+c=0$ строится график функции $y=ax^{2}+bx+c$
и отыскиваются абсциссы точек пересечения такого графика с осью .

Приём II[править | править код]

Для решения того же уравнения этим приёмом уравнение преобразуют к виду $ax^{2}=-bx-c$
и строят в одной системе координат графики квадратичной функции $y=ax^{2}$ и линейной функции y=-bx-c , затем находят абсциссу точек их пересечения.

Приём III[править | править код]

Данный приём подразумевает преобразование исходного уравнения к виду $a(x+l)^{2}+m=0$ , используя метод выделения полного квадрата суммы (разности) и затем в $a(x+l)^{2}=-m$ . После этого строятся график функции $y=a(x+l)^{2}$ (им является график функции $y=ax^{2}$ , смещённый на |l| единиц масштаба вправо или влево в зависимости от знака) и прямую y=-m , параллельную оси абсцисс. Корнями уравнения будут абсциссы точек пересечения параболы и прямой.

Приём IV[править | править код]

Квадратное уравнение преобразуют к виду $ax^{2}+c=-bx$ , строят график функции $y=ax^{2}+c$ (им является график функции $y=ax^{2}$ , смещённый на единиц масштаба вверх, если этот коэффициент положителен, либо вниз, если он отрицателен), и y=-bx , находят абсциссы их общих точек.

Приём V[править | править код]

Квадратное уравнение преобразуют к особому виду:

${displaystyle {dfrac {ax^{2}}{x}}+{dfrac {bx}{x}}+{dfrac {c}{x}}={dfrac {0}{x}};}$

${displaystyle ax+b+{dfrac {c}{x}}=0;}$

затем

${displaystyle ax+b=-{dfrac {c}{x}}.}$

Совершив преобразования, строят графики линейной функции y=ax+b и обратной пропорциональности $y=-{frac {c}{x}}; (cnot =0)$ , отыскивают абсциссы точек пересечения этих графиков. Этот приём имеет границу применимости: если c=0 , то приём не используется.

Решение квадратных уравнений с помощью циркуля и линейки[править | править код]

Описанные выше приёмы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.

Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.

Построить в системе координат окружность с центром в точке ${displaystyle Sleft(-{dfrac {b}{2a}};{dfrac {a+c}{2a}}right)}$ , пересекающую ось в точке .
Далее возможны три случая:

Доказательство

Иллюстрация к доказательству.

Рассматриваемый способ предполагает построение окружности, пересекающей ось ординат в точках (точке), абсциссы которых являются корнями (или корнем) решаемого уравнения. Как нужно строить такую окружность? Предположим, что она уже построена. Окружность определяется однозначно заданием трёх своих точек. Пусть в случае, если корня два, это будут точки $A(x_{1};0),B(x_{2};0),C(0;1)$ , где $x_{1},x_{2}$ , естественно, действительные корни квадратного уравнения (подчёркиваем: если они имеются). Найдём координаты центра такой окружности. Для этого докажем, что эта окружность проходит через точку $D(0;{frac {c}{a}})$ . Действительно, согласно теореме о секущих, в принятых обозначениях выполняется равенство (см рисунок). Преобразовывая это выражение, получаем величину отрезка OD, которой и определяется искомая ордината точки D: ${displaystyle OD={dfrac {OAcdot OB}{OC}}={frac {x_{1}x_{2}}{1}}={frac {c}{a}}}$ (в последнем преобразовании использована теорема Виета (см. ниже в одноимённом разделе)). Если же корень один, то есть ось абсцисс будет касательной к такой окружности, и окружность пересекает ось y в точке с ординатой 1, то она обязательно пересечёт её и в точке с указанной выше ординатой (в частности, если 1=c/a, это могут быть совпадающие точки), что доказывается аналогично с использованием уже теоремы о секущей и касательной, являющаяся частным случаем теоремы о секущих. В первом случае ( ${displaystyle {dfrac {c}{a}}not =1}$ ), определяющими будут точка касания, точка оси y с ординатой 1, и её же точка с ординатой ${displaystyle {dfrac {c}{a}}}$ . Если c/a и 1 – совпадающие точки, а корня два, определяющими будут эта точка и точки пересечения с осью абсцисс. В случае, когда (1=c/a) и корень один, указанных сведений достаточно для доказательства, так как такая окружность может быть только одна – её центром будет вершина квадрата, образуемого отрезками касательных и перпендикулярами, а радиус – стороне этого квадрата, составляющей 1. Пускай S – центр окружности, имеющей с осью абсцисс две общие точки. Найдём его координаты: для этого опустим от этой точки перпендикуляры к координатным осям. Концы этих перпендикуляров будут серединами отрезков AB и CD – ведь треугольники ASB и CSD равнобедренные, так как в них AS=BS=CS=DS как радиусы одной окружности, следовательно, высоты в них, проведённые к основаниям, также являются и медианами. Найдём координаты середин названных отрезков. Так как парабола симметрична относительно прямой ${displaystyle x=-{dfrac {b}{2a}}}$ , то точка этой прямой с такой же абсциссой будет являться серединой отрезка AB. Следовательно, абсцисса точки S равна этому числу. В случае же, если уравнение имеет один корень, то ось x является касательной по отношению к окружности,поэтому, согласно её свойству, её радиус перпендикулярен оси, следовательно, и в этом случае указанное число – абсцисса центра. Её ординату найдём так: ${displaystyle {dfrac {CD}{2}}={dfrac {OC+(OC+CD)}{2}}={dfrac {OC+OD}{2}}={dfrac {1+{dfrac {c}{a}}}{2}}={dfrac {a+c}{2a}}}$ . В третьем из возможных случаев, когда ca=1 (и, значит, a=c), то ${displaystyle {dfrac {c}{a}}=1={dfrac {2a}{2a}}={dfrac {a+c}{2a}}}$ .

Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке ${displaystyle S(-{dfrac {b}{2a}};{dfrac {c+a}{2a}})}$ , проходящую через точку C(0;1) , то она, в случаях, когда уравнение имеет действительные корни, пересечёт ось x в точках, абсциссы которых есть эти корни. Причём, если длина радиуса больше длины перпендикуляра к оси Ox, то уравнение имеет два корня (предположив обратное, мы бы получили противоречие с доказанным выше), если длины равны, то один (по той же причине), если же длина радиуса меньше длины перпендикуляра, то окружность не имеет общих точек с осью x, следовательно, и действительных корней у уравнения нет (доказывается тоже от противного: если корни есть, то окружность, проходящая через A, B, C совпадает с данной, и поэтому пересекает ось, однако она не должна пересекать ось абсцисс по условию, значит, предположение неверно).

Корни квадратного уравнения на множестве комплексных чисел[править | править код]

Уравнение с действительными коэффициентами[править | править код]

Квадратное уравнение с вещественными коэффициентами a,~b,~c всегда имеет с учётом кратности два комплексных корня, о чём гласит основная теорема алгебры. При этом, в случае неотрицательного дискриминанта корни будут вещественными, а в случае отрицательного — комплексно-сопряжёнными:

Уравнение с комплексными коэффициентами[править | править код]

В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два корня единичной кратности).

Корни приведённого квадратного уравнения[править | править код]

Квадратное уравнение вида $x^{2}+px+q=0,$ в котором старший коэффициент равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до

$x_{1,2}=-{frac {p}{2}}pm {sqrt {left({frac {p}{2}}right)^{2}-q}}.$

Мнемонические правила:

Из «Радионяни»:

«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное^[2] q.

Из «Радионяни» (второй вариант):

p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.

Из «Радионяни» (третий вариант на мотив Подмосковных вечеров):

Чтобы x найти к половине p,

Взятой с минусом не забудь,
Радикал приставь с плюсом минусом,
Аккуратно, не как-нибудь.
А под ним квадрат половины p,

Ты, убавь на q и конец,
Будет формула приведенная,
Рассуждений твоих венец.
Будет формула приведенная,
Рассуждений твоих венец.

Теорема Виета ^[3][править | править код]

Формулировка для приведённого квадратного уравнения[править | править код]

Сумма корней приведённого квадратного уравнения $x^{2}+px+q=0$ (вещественных или комплексных) равна второму коэффициенту , взятому с противоположным знаком, а произведение этих корней — свободному члену :

$x_{1}+x_{2}=-p,quad x_{1}x_{2}=q.$

С его помощью приведённые уравнения можно решать устно:

Для неприведённого квадратного уравнения[править | править код]

В общем случае, то есть для неприведённого квадратного уравнения ${displaystyle ax^{2}+bx+c=0colon }$

${displaystyle {begin{cases}x_{1}+x_{2}=-b/a,\x_{1}x_{2}=c/a.end{cases}}}$

На практике (следуя методу «переброски») для вычисления корней применяется модификация теорема Виета:

${displaystyle {begin{cases}x_{1}+x_{2}=-b/a&mid cdot a,\x_{1}x_{2}=c/a&mid cdot a^{2};end{cases}}}$

${displaystyle {begin{cases}(ax_{1})+(ax_{2})=-b,\(ax_{1})(ax_{2})=ac,end{cases}}}$

по которой можно устно находить ax₁, ax₂, а оттуда — сами корни:

Но у некоторых неприведённых уравнений корни можно устно угадать даже по стандартной теореме Виета:

Разложение квадратного трёхчлена на множители и теоремы, следующие из этого[править | править код]

Если известны оба корня квадратного трёхчлена, его можно разложить по формуле

${displaystyle ax^{2}+bx+c=a(x-x_{1})(x-x_{2})}$

(2)

Доказательство[править | править код]

Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни $x_{1}$ и $x_{2}$ квадратного уравнения $ax^{2}+bx+c=0$ образуют соотношения с его коэффициентами: ${displaystyle x_{1}+x_{2}=-{frac {b}{a}}, x_{1}x_{2}={frac {c}{a}}}$ . Подставим эти соотношения в квадратный трёхчлен:

${displaystyle {begin{alignedat}{2}ax^{2}+bx+c&=a(x^{2}+{frac {b}{a}}x+{frac {c}{a}})=a(x^{2}-(x_{1}+x_{2})x+x_{1}x_{2})=\&=a(x^{2}-x_{1}x-x_{2}x+x_{1}x_{2})=a(x(x-x_{1})-x_{2}(x-x_{1}))\&=a(x-x_{1})(x-x_{2}).end{alignedat}}}$

В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

Из формулы (2) имеются два важных следствия:

Следствие 1[править | править код]

Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.

Доказательство[править | править код]

Пусть $ax^{2}+bx+c=(kx+m)(nx+l)$ . Тогда, переписав это разложение, получим:

$(kx+m)(nx+l)=k(x+{frac {m}{k}})n(x+{frac {l}{n}})=kn(x-(-{frac {m}{k}}))(x-(-{frac {l}{n}}))$

Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются $-{frac {m}{k}}$ и $-{frac {l}{n}}$ . Так как коэффициенты вещественны, то и числа, противоположные их отношениям также являются элементами множества .

Следствие 2[править | править код]

Если квадратный трёхчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.

Доказательство[править | править код]

Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве , что противоречит условию, а потому наше предположение неверно, и такой трёхчлен не раскладывается на линейные множители.

Для квадратичной функции:
f (x) = x² − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось абсцисс, x = −1 и x = 2, являются решениями квадратного уравнения: x² − x − 2 = 0.

Уравнения, сводящиеся к квадратным[править | править код]

Алгебраические[править | править код]

Уравнение вида $acdot f^{2}(x)+bcdot f(x)+c=0$ является уравнением, сводящимся к квадратному.

В общем случае оно решается методом введения новой переменной, то есть заменой где — множество значений функции , c последующим решением квадратного уравнения $acdot t^{2}+bcdot t+c=0$ .

Также при решении можно обойтись без замены, решив совокупность двух уравнений:

$f(x)={frac {-b-{sqrt {b^{2}-4cdot acdot c}}}{2a}}$

$f(x)={frac {-b+{sqrt {b^{2}-4cdot acdot c}}}{2a}}$

К примеру, если $f(x)=x^{2}$ , то уравнение принимает вид:

${displaystyle ax^{4}+bx^{2}+c=0.}$

Такое уравнение 4-й степени называется биквадратным^[4]^[1].

С помощью замены

$y=x+{dfrac {k}{x}}$

к квадратному уравнению сводится уравнение

$ax^{4}+bx^{3}+cx^{2}+kbx+k^{2}a=0,$

известное как возвратное или обобщённо-симметрическое уравнение^[1].

Дифференциальные[править | править код]

Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка

подстановкой $y=e^{kx}$ сводится к характеристическому квадратному уравнению:

$k^{2}+pk+q=0$

Если решения этого уравнения $k_{1}$ и $k_{2}$ не равны друг другу, то общее решение имеет вид:

$y=Ae^{k_{1}x}+Be^{k_{2}x}$

, где

— произвольные постоянные.

Для комплексных корней $k_{1,2}=k_{r}pm k_{i}i$ можно переписать общее решение, используя формулу Эйлера:

${displaystyle y=e^{k_{r}x}left(Acos {k_{i}x}+Bsin {k_{i}x}right)=Ce^{k_{r}x}cos(k_{i}x+varphi ),}$

где A, B, C, φ — любые постоянные. Если решения характеристического уравнения совпадают $k_{1}=k_{2}=k$ , общее решение записывается в виде:

$y=Axe^{kx}+Be^{kx}$

Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.

Примечания[править | править код]

Литература[править | править код]

Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.

Ссылки[править | править код]

Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом Архивная копия от 28 января 2016 на Wayback Machine / Фестиваль педагогических идей «Открытый урок».
Математические методы

Источник

Уравнения квадратичной функции

Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:

Каноническая.
Квадратичная.
Общая.

В первой форме она имеет следующий вид: y² = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x² = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).

Рисунок 2. Директриса и фокус.

Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y²]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y²]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y² = 2px).

Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax² + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax². В этом случае формула нахождения вершины параболы выглядит таким образом:

Абсцисса вершины параболы: xa = -b / 2a.
Координата «игрек» по оси ординат: yb = — D / 2a.

В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b² — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.

Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax² + Bxy + Cy² + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).

В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.

Видео

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x ²+11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Алгоритм построения

В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:

Если вершина не задана, то нужно найти ее любым из методов.
Определить точки пересечения с осями декартовой системы координат.
Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
Выполнить построение, соединив точки.

Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x² + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.

Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.

Решение неполных квадратных уравнений

Как решить уравнение ax² = 0

Как решить уравнение ax² + с = 0

В двух словах

Как решить уравнение ax² + bx = 0

Квадратное уравнение

Что такое квадратное уравнение и как его решать?

Формулы корней квадратного уравнения

Примеры решения квадратных уравнений

Примеры решения задач

Как найти икс нулевое

Решение квадратных уравнений

Дискриминант

Корни квадратного уравнения

Неполные квадратные уравнения

Исторические сведения о квадратных уравнениях[править | править код]

Древний Вавилон[править | править код]

Индия[править | править код]

Корни квадратного уравнения на множестве действительных чисел[править | править код]

I способ. Общая формула для вычисления корней с помощью дискриминанта[править | править код]

II способ. Корни квадратного уравнения при чётном коэффициенте b[править | править код]

III способ. Решение неполных квадратных уравнений[править | править код]

IV способ. Использование частных соотношений коэффициентов[править | править код]

Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту[править | править код]

Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю[править | править код]

V способ. Разложение квадратного трёхчлена на линейные множители[править | править код]

Использование формулы квадрата суммы (разности)[править | править код]

Выделение полного квадрата суммы (разности)[править | править код]

VI способ. Использование прямой и обратной теоремы Виета[править | править код]

VII способ. Метод «переброски»[править | править код]

Графическое решение квадратного уравнения[править | править код]

Графический способ решения квадратных уравнений[править | править код]

Приём I[править | править код]

Приём II[править | править код]

Приём III[править | править код]

Приём IV[править | править код]

Приём V[править | править код]

Решение квадратных уравнений с помощью циркуля и линейки[править | править код]

Корни квадратного уравнения на множестве комплексных чисел[править | править код]

Уравнение с действительными коэффициентами[править | править код]

Уравнение с комплексными коэффициентами[править | править код]

Корни приведённого квадратного уравнения[править | править код]

Теорема Виета [3][править | править код]

Формулировка для приведённого квадратного уравнения[править | править код]

Для неприведённого квадратного уравнения[править | править код]

Разложение квадратного трёхчлена на множители и теоремы, следующие из этого[править | править код]

Доказательство[править | править код]

Следствие 1[править | править код]

Доказательство[править | править код]

Следствие 2[править | править код]

Доказательство[править | править код]

Уравнения, сводящиеся к квадратным[править | править код]

Алгебраические[править | править код]

Дифференциальные[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Уравнения квадратичной функции

Видео

Построение параболы

Алгоритм построения

Теги

Вам также может понравиться

Дорога памяти как найти человека по фамилии

На ноутбуке рабочий стол вверх ногами как исправить

Как его собрать найди видео

Добавить комментарий Отменить ответ

Теорема Виета ^[3][править | править код]