Как найти нули функции аналитически - Сайт, где вы сможете решить свои вопросы

Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Запомните!

Нули функции — это
значения « x »
(аргумента функции),

при которых « y = 0 ».

В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу

(аналитически). Разберем алгоритм решения

подобных задач.

Как найти нули функции, заданной формулой

Важно!

Чтобы найти нули функции, нужно:

в формулу функции вместо

« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»;
решить полученное уравнение
относительно « x »;
записать полученные решения уравнения для « x » в ответ.

По традиции разберемся на примере.

Разбор примера

Найдите нули функции:

Подставим вместо значения функции « f(x) » ноль.

0 = 0,2x + 3

Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».

Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.

−0,2x = 3 | · (−1)

0,2x = −3

Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.

0,2x = −3

· x = −3 | · 10

· x · 10 = −3 · 10

· x = −30

2x = −30

x =

x = −15

Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3

Разбор примера

Найдите нули функции:

Вместо « f(x) » подставим ноль.

0 = x ³ − 4x

−x ³ + 4x = 0 | · (−1)

(−1) · (−x ³ + 4x) = 0 · (−1)

x ³ − 4x = 0

Вынесем общий множитель
« x » за скобки.

В левой части полученного уравнения у нас два множителя:
« x »
и «(x ² − 4)». Результат их умножения равен нулю.

Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x ² − 4)»
равен нулю.

Решаем квадратное уравнение
«x ² − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.

a · x ² + b · x + c = 0

x_1;2 =

x ² − 4 = 0

x_1;2 =

0 ±
√0² − 4 · 1 · (−4)

2 · 1

x_1;2 =

Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.

Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x ³ − 4x

Разбор примера

Найдите нули функции:

Подставим вместо « h(x) » ноль.

Перенесем правую часть

в левую, изменив ее знак на минус.

Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x ² − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.

Решим полученное квадратное уравнение через формулу с дискриминантом.

a · x ² + b · x + c = 0

x_1;2 =

x ² − x − 6 = 0

x_1;2 =

−(−1) ±
√(−1)² − 4 · 1 · (−6)

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 3	x₂ = −2

Ответ: x = −2; x = 3 являются нулями функции

h(x) =

Разбор примера

Найдите нули функции:

Заменим «f(x)» на ноль.

Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x ² − 4 = 0 »

будет равен нулю, когда его подкоренное выражение
« x ² − 4 »
будет равно нулю.

Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x ² − 4».

x_1;2 =

x ² − 4 = 0

x_1;2 =

−(−0) ±
√(−0)² − 4 · 1 · (−4)

2 · 1

x_1;2 =

Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x ² − 4

Как найти нули функции на графике функции

Важно!

Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).

По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.

Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».

Рассмотрим на примере.

Разбор примера

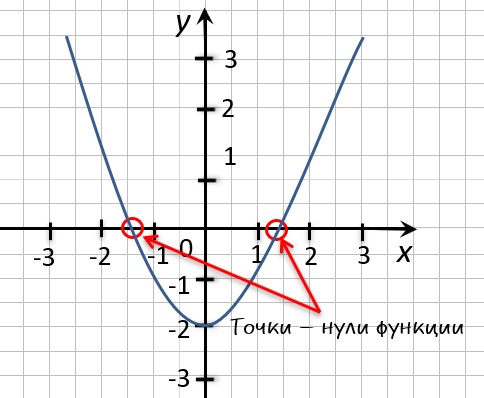
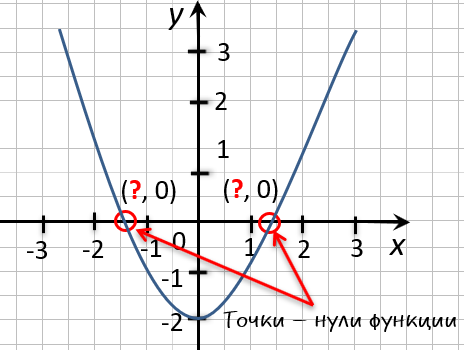
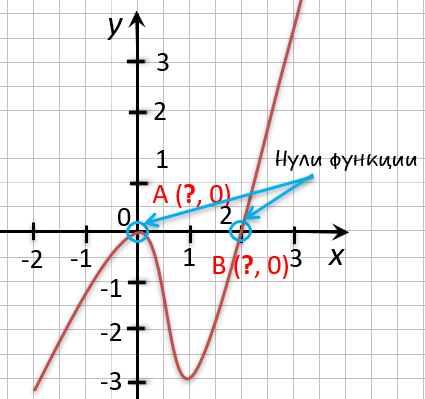
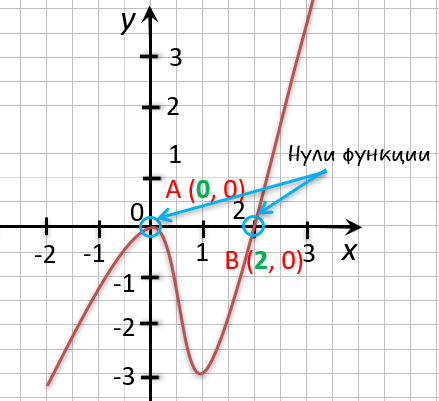
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.

Отметим на графике функции его точки пересечения с осью « Ox ».

Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось

« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.

Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».

На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».

Запишем полученные значения координат « x » в ответ.

Ответ: x = 0; x = 2 являются нулями функции.

Как найти нули функции, заданной таблицей

В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.

Разбор примера

Найдите нули функции, заданной таблицей.

x	−2	−1	0	1	2	3
y	−3	−1,5	0	2	1	0

Вспомним определение нулей функции.

Запомните!

Нули функции — это
значения « x » в функции,
при которых « y = 0 ».

Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.

x	−2	−1	0	1	2	3
y	−3	−1,5	0	2	1	0

Остаётся только записать в ответ значения « x » из таблицы.

Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Нули функции

Что такое нули функции? Как определить нули функции аналитически и по графику?

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

Примеры.

1) Найти нули линейной функции y=3x+15.

Решение:

Чтобы найти нули функции, решим уравнение 3x+15=0.

3x=-15; x= -5.

Таким образом, нуль функции y=3x+15 — x= -5.

Ответ:x= -5.

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Решение:

Для нахождения нулей функции решим квадратное уравнение

x²-7x+12=0.

Его корни x1=3 и x2=4 являются нулями данной функции.

Ответ: x=3; x=4.

3)Найти нули функции

$[g(x) = frac{{{x^2} + 5x + 4}}{{{x^2} - 1}}]$

Решение:

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0,x²≠1,x≠±1. То есть область определения данной функции (ОДЗ)

x ∈ (-∞; -1)U(-1; 1)U(1;∞).

Решаем уравнение

$[frac{{{x^2} + 5x + 4}}{{{x^2} - 1}} = 0 Leftrightarrow left{ begin{array}{l} {x^2} + 5x + 4\ {x^2} - 1 ne 0 end{array} right.]$

Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.

Ответ: x=-4.

Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.

Если график не пересекает ось Ox, функция не имеет нулей.

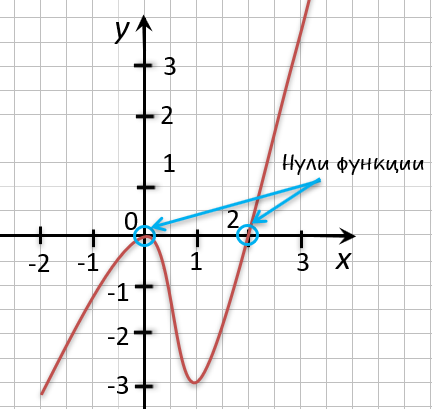
Например,

функция, график которой изображен на рисунке,имеет четыре нуля —

$[{x_1} = - 2;{x_2} = - 1;{x_3} = 1;{x_4} = 3.]$

В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.

Источник

Нули функции

Что такое нули функции? Как определить нули функции аналитически и по графику?

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

1) Найти нули линейной функции y=3x+15.

Чтобы найти нули функции, решим уравнение 3x+15 =0.

Таким образом, нуль функции y=3x+15 — x= -5 .

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Для нахождения нулей функции решим квадратное уравнение

Его корни x1=3 и x2=4 являются нулями данной функции.

3)Найти нули функции

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)

Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.

Если график не пересекает ось Ox, функция не имеет нулей.

функция, график которой изображен на рисунке,имеет четыре нуля —

Математика. Нули функции + примеры + инструкция

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

Примеры.

1) Найти нули линейной функции y=3x+15.

Чтобы найти нули функции, решим уравнение 3x+15=0.

Таким образом, нуль функции y=3x+15 — x= -5.

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Для нахождения нулей функции решим квадратное уравнение

Его корни x1=3 и x2=4 являются нулями данной функции.

1. Нуль функции – это такое значение довода х, при котором значение функции равно нулю. Впрочем нулями могут быть лишь те доводы, которые входят в область определения исследуемой функции. То есть в такое уйма значений, для которых функция f(x) имеет толк. 2. Запишите заданную функцию и приравняйте ее к нулю, скажем f(x) = 2х?+5х+2 = 0. Решите получившееся уравнение и обнаружьте его действительные корни. Корни квадратного уравнения вычисляются с поддержкой нахождения дискриминанта. 2х?+5х+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;х1 = (-b+?D)/2*а = (-5+3)/2*2 = -0,5;х2 = (-b-?D)/2*а = (-5-3)/2*2 = -2.Таким образом, в данном случае получены два корня квадратного уравнения, соответствующих доводам начальной функции f(x). 3. Все обнаруженные значения х проверьте на принадлежность к области определения заданной функции. Обнаружьте ООФ, для этого проверьте начальное выражение на наличие корней четной степени вида ?f (х), на присутствие дробей в функции с доводом в знаменателе, на наличие логарифмических либо тригонометрических выражений. 4. Рассматривая функцию с выражением под корнем четной степени, примите за область определения все доводы х, значения которых не обращают подкоренное выражение в негативное число (напротив функция не имеет смысла). Уточните, попадают ли обнаруженные нули функции в определенную область допустимых значений х. 5. Знаменатель дроби не может обращаться в нуль, следственно исключите те доводы х, которые приводят к такому итогу. Для логарифмических величин следует рассматривать лишь те значения довода, при которых само выражение огромнее нуля. Нули функции, обращающие подлогарифмическое выражение в нуль либо негативное число, обязаны быть отброшены из финального итога. Обратите внимание! При нахождение корней уравнения, могут возникнуть лишние корни. Проверить это легко: довольно подставить полученное значение довода в функцию и удостовериться обращается ли функция в нуль. Полезный совет Изредка функция не выражается в очевидном виде через свой довод, тогда легко нужно знать, что представляет собой эта функция. Примером этому может служить уравнение окружности.

Нулями функции называются значение абсциссы, при котором значение функции равно нулю.

Если функция задана своим уравнением, то нулями функции будут решения уравнения . Если задан график функции , то нули функции — это значения , в которых график пересекает ось абсцисс.

Нули функции онлайн

Одной из задач, возникающих при исследовании функции, является нахождение её нулей – т.е. точек пересения с осью абсцисс. Рассмотрим график некоторой функции :

Нулями функции являются точки в которых, как было сказано выше, график функции пересекает ось абсцисс. Чтобы найти нули функции необходимо и достаточно решить уравнение:

Нулями функции будут корни этого уравнения. Таким образом, нули функции находятся в точках .

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен найти нули практически любой, даже очень сложной функции.

[spoiler title=”источники:”]

http://multiurok.ru/files/matematika-nuli-funktsii-primery-instruktsiia.html

http://mathforyou.net/online/calculus/zeros/

[/spoiler]

Источник

Мы знакомы с примерами функций и способами их задания. Рассмотрим понятия области определения и области значения функции, а также свойства функции.
1. Область определения и область значений функции
Найти область определения функции можно как по формуле, задающей функцию, так и по графику.

Определение:
Область определения функции — это допустимые значения независимой переменной (переменной x). Обозначается область определения функции D(f).

Чтобы лучше понять что такое область определения функции рассмотрим несколько примеров.
Если функция задана аналитически:

Найти область определения функции, если она задана формулой:

1) y=12x+7

2)f(x)=(5x-3)/(8x-16)

Функция задана формулой значит, для того чтобы найти ее область определения, нужно ответить на вопрос: “Какие значения можно подставлять в формулу вместо х?”
1) В формулу функции вместо х можно подставлять

любые

действительные числа. Значит область определения функции – любые действительные числа. Записывают следующим образом:

D(y)=(-ထ; +ထ)

2) Поскольку знаменатель функции не должен равняться нулю:

8x-16≠0

х≠2

Значит, D(y)=(-ထ; 2)U(2; +ထ)

Найти область определения функции если она задана графически еще проще, для этого необходимо обратить внимание на то, какие значения принимает “х” на графике. Попробуйте выполнить задание самостоятельно, а затем сравните с решением.

По графику видно что D(f)=[-7;7]

Далее рассмотрим понятие область значений функции

Определение:
Область значений функции – это множество всех действительных значений y, которые принимает функция. Обозначается область значений функции E(f).

Рассмотрим примеры на нахождение области определения если функция задана аналитически и графически.

Для того чтобы найти область значений функции необходимо ответить на вопрос: ” какие значения может принимать у“

1) Если вместо х любое действительное число, то у, в данном случае, также может принимать любые значения, следовательно

E(y)=(-ထ; +ထ)

2) Так как, при подстановке любого действительного числа вместо х, функция (у) из-за модуля будет принимать только неотрицательные значения, то

E(y)=[0; +ထ)

Для нахождения области значений функции, если она задана графически необходимо обратить внимание на то, какие значения принимает “у” на графике. Попробуйте выполнить задание самостоятельно, а затем сравните с решением.

По графику видно что E(f)=[-7;7]

2. Нули функции

Нули функции можно найти как по формуле, задающей функцию, так и по графику.

Определение:
Нули функции– это значение аргумента, при которых функция обращается в ноль.

Если необходимо найти нули функции по графику, то нужно определить точки пересечения графика с осью ОХ:

На данном примере график функции пересекает ось ОХ при х=-4; х=5,5 и х=8. Эти точки пересечения выделены красным цветом.
Обратите внимание!:

Существуют функции, которые не будут иметь точек пересечения с осью ОХ, следовательно нулей у такой функции нет

Для того чтобы найти нули функции заданной аналитически нужно:

Прировнять “у” к нулю
Решить получившееся уравнение

а. y=-11х+22
б. y=(х+76)(х-95)

а. y=-11х+22
1) у=0
т.е:

-11х+22=0

2) Решим получившееся уравнение

-11х+22=0

-11х=-22

х=2

Ответ: 2
б. y=(х+76)(х-95)
1) у=0
получим:

(х+76)(х-95)=0

2) Решим уравнение

(х+76)(х-95)=0

х+76=0 или х-95=0

х=-76 х=95

Ответ: -76; 95

3. Промежутки знакопостоянства

Промежутки знакопостоянства функции также можно определить как по формуле, задающей функцию, так и по графику.

Определение:
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

Если необходимо найти промежутки знакопостоянства у функции заданной графически, то достаточно определить по графику где функция принимает положительные и отрицательные значения. Для примера возьмем график функции для которой мы находили нули функции :

На рисунке синим цветом выделены части графика в промежутках [-8; -4) U (-4; 5,5) U (8;9] , которые расположены выше оси ОХ. Зеленым цветом выделены части графика в промежутке (5,5 ; 8) который расположен выше оси х.
Значит, что в промежутках [-8; -4) U (-4; 5,5) U (8;9] функция принимает положительные значения, а в промежутке (5,5 ; 8) она принимает отрицательные значения. Это и есть промежутки знакопостоянства.

Что делать если функция задана аналитически?
Чтобы определить знаки постоянства достаточно понимать как решаются неравенства и запомнить алгоритм:

Рассматриваем случай когда у>0
Решаем получившееся неравенство, полученный промежуток показывает при каких “х” функция положительна
Аналогично рассматриваем случай у<0
Решаем неравенство, полученный промежуток показывает при каких “х” функция отрицательна

Рассмотрите пример с решением или попробуйте выполнить задание самостоятельно с помощью алгоритма описанного выше:

а. y=-11х+22
1) y>0
Следовательно

-11х+22>0

-11(x+2)>0

x+2<0

x<-2

3) y<0
Следовательно

-11х+22<0

-11(x+2)<0

x+2>0

x>2

Ответ: Функция положительна (у>0) при х∈ (-∞;-2)

Функция отрицательна (у<0) при х∈ (-2;+∞)

б. y=|x+14|
1) y>0
Следовательно

|x+14|>0

2) |x+14|>0

Неравенство верно при любых “х” кроме х=-14

3) y<0
Следовательно

|x+14|<0

4) |x+14|<0

Неравенство неверно при любых “х”

Ответ: Функция положительна (у>0) при х∈ (-∞;-14) U (-14;+∞)

Функция не принимает отрицательных значений

4. Монотонность

В курсе средней школы монотонность функции будем определять исключительно по ее графическому заданию, но в старших классах промежутки возрастания и убывания можно определить и аналитически с помощью производной

Определение:
Функцию у=f(x) называют возрастающей на промежутке, если для любых двух точек x1 и x2 промежутка, таких, что x1 < x2, выполняется неравенство f(x1) < f(x2)

Функцию у=f(x) называют убывающей на промежутке, если для любых двух точек x1 и x2 промежутка, таких, что x1 < x2, выполняется неравенство f(x1) > f(x2)

Иными словами формальное определение можно интерпретировать следующим образом:
Функция называется возрастающей на промежутке если график визуально “идет наверх”, аналогично функция называется убывающей если график визуально “идет вниз”.
В качестве примера найдем промежутки монотонности графика функции, рассматриваемого выше:

На рисунке голубым цветом выделены части графика в промежутках (-4; 1) U (7;9) на которых график функции возрастает. Розовым цветом выделены части графика в промежутке (-8 ; 4) U (1;7) на которых график функции убывает. Это и есть промежутки монотонности исходной функции.

5. Четность и нечетность

Исследовать функцию на четность и нечетность можно как аналитически так и графически. Рассмотрим определения четной и нечетной функции, а также алгоритмы для ее проверки.

Определение:
Функцию у=f(x) называют четной, если для любого значения “х” выполняется равенство f(-x)=f(x)
Функцию у=f(x) называют нечетной, если для любого значения “х” выполняется равенство f(-x)=-f(x)

Важно!

Существуют четные функции, нечетные функции, а также функции которые не являются ни четными, ни нечетными.

Не существует функций которые одновременно являются четными и нечетными

Если функция y=f(x) задана аналитически, то для ее исследования на четность и нечетность применим следующий алгоритм:

Записать выражение y=f(-x). Для этого необходимо в формуле задания функции заменить “х” на “-х”;
Сопоставить выражения f(-x) и f(x):

Если f(-x) = f(x), то функция является четной;
Если f(-x) = -f(x), то функция является нечетной;
Если ни первое, ни второе условие не выполняется то функция не является ни четной, ни нечетной.

Рассмотрим пример:

а. y=-11х+22

1) f(-x)= -11·(-x)+22=11х+22
2) Сравним f(x) и f(-x)
-11х+22 ≠ 11х+22, то есть f(-x) ≠ f(x)
-11х+22 ≠ -(-11х-22), то есть f(-x) ≠ -f(x)
Значит, функция не является четной и не является нечетной

б. y=|x|

1) f(-x)=|-x|
2) Сравним f(x) и f(-x)
|x|=|-x|, то есть f(-x) = f(x)
Значит функция является четной

Если функция y=f(x) задана графически, то для ее исследования на четность и нечетность будем применять следующие правила:

Четная и нечетная функция y=f(x) имеет симметричную область определения D(f)

Если график функции y=f(x) симметричен относительно оси ординат, то y=f(x) – четная функция
Например:

Если график функции y=f(x) симметричен относительно начала координат, то y=f(x) – четная функция
Например:

На этом рассмотрение свойств функций закончено. Помимо тех свойств, которые разобраны в данном разделе существуют и другие, такие как ограниченность и неограниченность функции, периодичность функции и так далее, которые в курсе алгебры 7-9 класса не рассматриваются.

Источник

Нули аналитических функций

Пусть функция f(z) является аналитической в точке z_0 .

Точка z_0 называется нулем функции f(z) , если ее значение в этой точке равно нулю, т.е. f(z_0)=0 .

В разложении функции в ряд Тейлора в окрестности нуля этой функции отсутствует свободный член: c_0=f(z_0)=0 . Если при этом в разложении отсутствуют и слагаемые, содержащие степени разности (z-z_0) до n-й степени, т.е. разложение имеет вид

$f(z)= sum_{k=n}^{infty}c_k(z-z_0)^k,quad f(z)=c_n(z-z_0)^n+ c_{n+1}(z-z_0)^{n+1}+ ldots,quad c_nne0,$

(3.20)

то точка z_0 называется нулем порядка функции f(z) . Нуль первого порядка называется простым нулем.

Правую часть равенства (3.20) можно записать в виде произведения:

$f(z)=(z-z_0)^ncdot bigl[c_n+c_{n+1}(z-z_0)+ldotsbigr]$ , или f(z)= (z-z_0)^ncdot bigl[b_0+b_1(z-z_0)+ldotsbigr] ,

где второй множитель можно рассматривать как степенной ряд, сходящийся в точке z_0 , поэтому его сумма — функция, аналитическая в точке z_0 ; обозначим ее varphi(z) . Таким образом, из (3.20) получаем представление функции f(z) в виде

f(z)=(z-z_0)^ncdot varphi(z),qquad varphi(z_0)=c_nne0.

(3.21)

Кроме того, используя формулу коэффициентов ряда Тейлора $c_n=frac{f^{(n)}(z_0)}{n!}$ , находим, что для нуля порядка функции f(z) в точке z_0 справедливо условие

$f^{(n)}(z_0)ne0,qquad f^{(k)}(z_0)=0,quad k=0,1,2,ldots,(n-1),$

(3.22)

т.е. порядок нуля функции определяется порядком первой отличной от нуля в этой точке производной.

Пусть функция f(z) задана в виде произведения f(z)=f_1(z)cdot f_2(z) и точка z_0 является нулем порядка для f_1(z) и нулем порядка для f_2(z) . Тогда, используя условие (3.21) для этих функций, можно записать

f(z)= (z-z_0)^kcdot varphi_1(z)cdot (z-z_0)^mcdot varphi_2(z),

или

$f(z)= (z-z_0)^{m+k}cdot varphi(z),qquad varphi(z)= varphi_1(z)cdot varphi_2(z),quad varphi(z_0)ne0.$

(3.23)

Это означает, что порядок нуля в точке z_0 функции, полученной в результате перемножения аналитических функций, равен сумме порядков нуля в этой точке функций-сомножителей.

Сформулируем вывод в виде следующего утверждения.
Утверждение 3.5

1. Точка z_0 является нулем функции f(z) , если f(z_0)=0 ; нулем порядка -если для коэффициентов ряда Тейлора ее разложения по степеням (z-z_0) справедливы равенства

c_k=0,quad k=0,1,2,ldots,(n-1),quad c_nne0.

2. Следующие условия являются необходимыми и достаточными условиями пуля порядка п функции f(z) в точке z_0colon

а) условие (3.22): $f^{(n)}(z_0)ne0,~~ f^{(k)}(z_0)=0,~ k=0,1,1,ldots,(n-1)$ ;
б) представление функции в виде произведения (3.21): f(z)=(z-z_0)^ncdot varphi(z),~~ varphi(z_0)=c_nne0 .

Замечания 3.3

1. Если функция не определена в точке z_0 , но $limlimits_{zto z_0}f(z)=0$ , то после доопределения функции в точке $z_0colon, f(z_0)= limlimits_{zto z_0}f(z)$ , точку z_0 тоже называют нулем функции. Например, для функции $f(z)=frac{sin^2z}{z}$ , доопределенной в точке $z_0=0colon, f(z)= begin{cases}dfrac{sin^2z}{z},& zne0,\ 0,& z=0,end{cases}$ точка z_0=0 является нулем.

2. Пусть f(z) представлена в виде отношения $frac{f_1(z)}{f_2(z)}$ аналитических в точке z_0 функций и точка z_0 является нулем порядка для числителя и нулем порядка — для знаменателя. При условии k>m , доопределив функцию f(z) , выше, получим, z_0 — нуль функции f(z) .

Используя условие (3.21) для функций f_1(z) и f_2(z) , получаем равенство $f(z)= frac{(z-z_0)^k varphi_1(z)}{(z-z_0)^m varphi_2(z)}$ , или $f(z)= (z-z_0)^{k-m} varphi(z)$ . Здесь — аналитическая в точке z_0 , так как и — аналитические в этой точке и varphi_2(z_0)ne0 . Кроме того, varphi(z_0)ne0 , так как varphi_1(z_0)ne0 . Поэтому для функции f(z) точка z_0 является нулем порядка (k-m) (см. (3.21)). Порядок нуля частного равен разности — из порядка нуля числителя вычитается порядок нуля знаменателя.

Алгоритм нахождения нулей аналитических функций и определения их порядков

1. Найти нули аналитической функции f(z) , решая уравнение f(z)=0 .

2. Определить порядок каждого полученного нуля z_0 . Для этого выполнить одно из следующих действий:

а) разложить f(z) в ряд по степеням (z-z_0) . Младшая степень разности (z-z_0) , присутствующая в разложении (3.20), определяет порядок нуля z_0 ;

б) найти производные $f^{(k)}(z)$ и их значения в нуле функции, т.е. $f^{(k)}(z_0)$ . Порядок нуля z_0 функции f(z) определяется порядком первой, не равной нулю в точке производной;

в) записать функцию в виде произведения (3.21); степень разности (z-z_0) в этом произведении определяет порядок нуля z_0 ;

г) записать функцию в виде произведения более простых функций и для каждой из них определить порядок нуля z_0 по одному из изложенных в предыдущих пунктах правилу. Порядок нуля го произведения равен сумме порядков нуля сомножителей.

3. Для функции f(z) , не определенной в точке z_0 , но удовлетворяющей в этой точке условию $limlimits_{zto z_0}f(z)=0$ , порядок нуля го определить по правилам, изложенным в п. 2 или в соответствии с замечанием 3.3.

Пример 3.26. Найти все нули функции f(z)=z^5-z^4+4z^3-4z^2 , определить их порядок.

Решение. Воспользуемся алгоритмом.

1. Раскладываем многочлен на множители: f(z)=z^4(z-1)+4z^2(z-1)= z^2(z-1)(z^2+4) . Находим нули функции: $z_1=0,~ z_2=1,~z_{3,4}=pm2i$ . Разложение многочлена на линейные множители имеет вид f(z)=z^2(z-1)(z-2i)(z+2i) .

2. Определяем порядок каждого нуля. Удобнее использовать для этого формулу (3.21). Для точки z_1=0 из равенства f(z)= z^2cdot varphi(z),~ varphi(0)ne0 , получаем, что z=0 — нуль второго порядка; для точки z_2=1 из равенства f(z)= (z-1)cdot varphi(z),~ varphi(1)ne0 , получаем, что z=1 — нуль первого порядка (простой нуль); для точек $z_{3,4}=pm2i$ аналогично находим, что это нули первого порядка (простые нули) данной функции.

Пример 3.27. Определить порядок нуля z_0=0 для функций:

а) $f(z)=e^{z^2}-1-z^2$ ; б) f(z)=sin^3z-1+cos z .

Решение. а) Для определения порядка нуля z_0=0 удобно использовать определение, т.е. разложить функцию по степеням (п. 2″а” алгоритма). Получаем

$e^{z^2}-1-z^2= left(1+z^2+frac{z^4}{2!}+ldotsright)-1-z^2= frac{z^4}{2!}+ frac{z^6}{3!}+ldots$

Так как в полученном разложении коэффициент $c_4=frac{1}{2}$ , т.е. не равен нулю, а предыдущие равны нулю (c_0=c_1=c_2=c_3=0) , то заключаем, что точка z_0=0 является нулем порядка n=4 для данной функции.

б) В данном случае используем формулу (3.22), т.е. п. 2″б” алгоритма. Находим значения производных функции в точке z_0=0colon

$begin{gathered} f'(z)= 3sin^2zcdotcos z-sin z,quad f'(0)=0;\ f''(z)= 6sin zcdot cos^2z-3sin^3z-cos z,quad f''(0)=-1ne0.end{gathered}$

Следовательно, точка z_0=0 является нулем второго порядка (n=2) данной функции.

Пример 3.28. Определить порядок нуля функции $f(z)=bigl(e^{z^2}-1-z^2bigr)sin^3z$ в точке z_0=0 .

Решение. Функция записана в виде произведения двух функций. Для первого множителя $f_1(z)=e^{z^2}-1-z^2$ порядок нуля в точке z_0=0 определен в предыдущем примере: k=4 . Для функции sin z точка z_0=0 — нуль первого порядка, так как согласно п. 2″б” алгоритма f'(0)=cos0=1ne0 . Поэтому, учитывая, что f_2(z)=sin^3z= (sin z)^3=sin zsin zsin z и пользуясь п. 2″г” алгоритма, получаем, что z_0=0 — нуль третьего порядка (m=3) . Поскольку f(z)=f_1(z)cdot f_2(z) , то по правилу 2″г” алгоритма получаем результат — точка z_0=0 является нулем седьмого порядка заданной функции, так как n=k+m=7 .

Пример 3.29. Найти нули функций а) $frac{sin^3z}{z}$ и б) $frac{e^{2z}-1}{sin z}$ ; определить их порядок.

Решение. а) Равенство f(z)=0 в области определения функции выполняется для точек , таких, что

sin^3z=0,~~ zne0 , то есть z_k=kpi,~~ k=pm1,pm2,ldots .

Эти точки, очевидно, простые нули функции sin z , а потому нули третьего порядка для функции sin^3z . Поэтому для каждого нуля z_k , используя необходимое условие (см. п. 2 утверждения 3.5), можно записать sin^3z= (z-z_k)^3 varphi_1(z),~ varphi_1(z_k)ne0 и, следовательно, $frac{sin^3z}{z}= (z-z_k)^3 varphi(z),~ varphi(z_k)ne0$ . Из этого, в силу достаточного условия (3.21) (см. п. 2 утверждения 3.5), заключаем, что точки z_k=kpi,~ k=pm1,pm2,ldots являются нулями третьего порядка данной функции. Кроме того, так как выполняется условие $limlimits_{zto0} frac{sin^3z}{z}= limlimits_{zto0} frac{sin z}{z}cdotsin^2z=0$ , то, после доопределения функции (см. п.1 замечаний 3.3 ), получаем, что z_0=0 является нулем функции. Чтобы определить порядок нуля, используем результат, полученный в п.2 замечаний 3.3. А именно, для функции, стоящей в числителе, точка z=0 — нуль третьего порядка (k=3) , а для знаменателя, очевидно, простой нуль (m=1) . Поэтому z=0 — нуль второго порядка данной функции.

б) Нулями функции в области определения zne kpi,~ kinmathbb{Z} являются точки z_k=kpi i,~ k=pm1,pm2,ldots — корни уравнения $e^{2z}=1,~ zne0$ . Эти точки — простые нули числителя и $e^{2z}-1= (z-z_k)varphi_1(z),~ varphi_1(z_k)ne0$ . Поэтому из равенства $f(z)=frac{z-z_k}{sin z}varphi_1(z)$ или f(z)=(z-z_k)varphi(z),~ varphi(z_k)ne0 заключаем, что z_k=kpi i,~ k=pm1,pm2,ldots — простые нули данной функции.

В точке z=0 , которая также является нулем числителя, функция не определена. Найдем предел функции в этой точке. Для раскрытия неопределенности $limlimits_{zto0} frac{e^{2z}-1}{sin z}$ можно использовать свойства пределов, или разложить по степеням числитель и знаменатель:

$limlimits_{zto0} frac{e^{2z}-1}{sin z}= limlimits_{zto0} frac{left(1+2z+ frac{(2z)^2}{2!}+ldotsright)-1}{z-frac{z^3}{3!}+ldots}= limlimits_{zto0} frac{z left(2+ frac{4z}{2!}+ldotsright)}{z left(1-frac{z^2}{3!}+ldotsright)}= 2.$

Так как $limlimits_{zto0}f(z)ne0$ , то точка z=0 не является нулем данной функции.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Как найти нули функции, заданной формулой

Разбор примера

Разбор примера

Разбор примера

Разбор примера

Как найти нули функции на графике функции

Разбор примера

Как найти нули функции, заданной таблицей

Разбор примера

Ваши комментарии

Нули функции

Математика. Нули функции + примеры + инструкция

Нули функции онлайн

Нули аналитических функций

Алгоритм нахождения нулей аналитических функций и определения их порядков

Вам также может понравиться

Телешоу ты как меня нашел видео

Париж как найти работу

Можно найти как подчеркнуть

Добавить комментарий Отменить ответ