Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу
(аналитически). Разберем алгоритм решения
подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.
По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
Вместо « f(x) » подставим ноль.
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель
« x » за скобки.
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x 2 − 4)»
равен нулю.
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.
Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
Подставим вместо « h(x) » ноль.
Перенесем правую часть
в левую, изменив ее знак на минус.
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции
h(x) =
Разбор примера
Найдите нули функции:
Заменим «f(x)» на ноль.
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0)2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.
Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».
Рассмотрим на примере.
Разбор примера
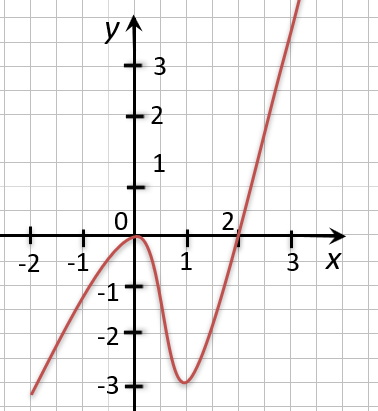
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.
Отметим на графике функции его точки пересечения с осью « Ox ».
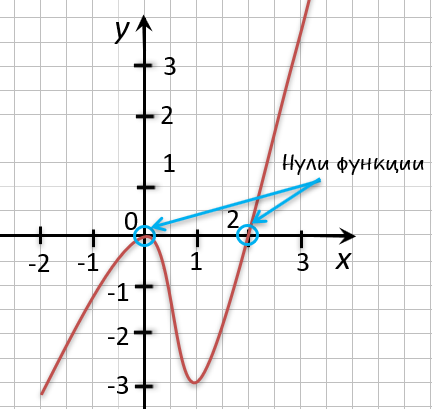
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
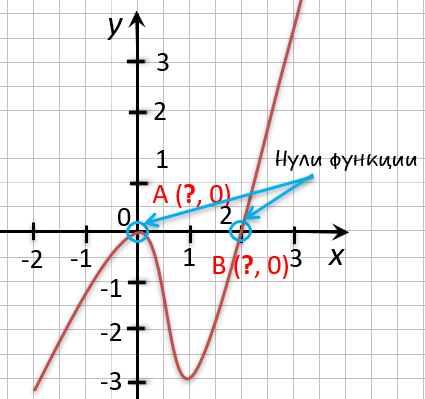
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
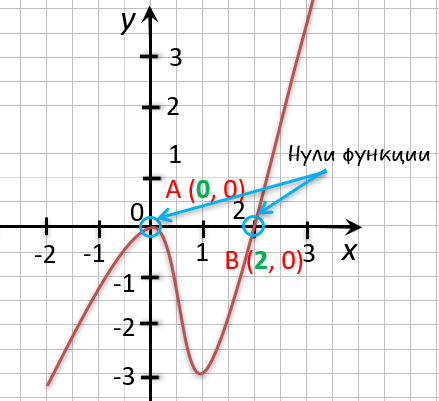
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
Найдите нули функции, заданной таблицей.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом: 
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
- а) у= –11х +22
- б) у= (х + 76)(х – 95)
- в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
- Находим х, разделив 22 на 11: х=22:11
- Получим х=2.
- Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0.
Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95.
Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Метод интервалов: примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x) или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
произведение линейных двучленов с коэффициентом 1 при переменной х;
произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
- (x+3)·(x2−x+1)·(x+2)3≥0,
- (x-2)·(x+5)x+3>0 ,
- (x−5)·(x+5)≤0,
- (x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
- наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки или ≥, то выделяем штриховкой участки, отмеченные знаком «+».
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x-5x+1>0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: (−∞, −1), (−1, 5) и (5, +∞).
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t
Нули функции – это значения переменной, которые делают функцию равной нулю. Например, нулями f (x) = x ^ 2-1 являются x = 1 и x = -1. Здесь каретка ^ обозначает возведение в степень. В Excel вы можете использовать приложение Solver, чтобы найти ноль для функции, используя методы из области математики, называемой «численный анализ». Вам не нужно знать подробности метода. Все, что вам нужно сделать, это придумать точную догадку относительно одного из нулей функции, и Excel завершит работу.
Введите свою функцию в ячейку A1 электронной таблицы Excel, используя вместо нее ячейку A2. Например, если ваша функция f (x) = x ^ 2-1, введите в ячейку A1 точно следующее: = A2 ^ 2-1.
Введите свое лучшее предположение в ячейку A2 относительно того, что является нулем f (x). Например, для f (x) = x ^ 3-3x + 10 вы можете ввести число от -2 до -1 в ячейку A2, заметив, что f (-2) равно -11, а f (-1) +12. Так как они находятся на противоположных сторонах нуля на числовой линии, ноль для f (x) существует между x = -1 и x = -2.
Перейдите в раскрывающееся меню Инструменты в верхней части страницы и выберите Solver. Панель Solver появится.
Введите A1 в поле «Задать целевую ячейку».
Выберите переключатель «Значение» и введите число 0, потому что вы хотите, чтобы Excel сделал A1 равным нулю.
Введите А2 в поле «Путем изменения ячеек».
Нажмите кнопку «Решить». Ноль, который вычисляет Excel, появится в ячейке A2. Солвер спросит вас, хотите ли вы сохранить решение. Выберите «ОК».
Решите для другого нуля той же функции, введя другое значение, снова убедившись, что оно близко к тому месту, где вы подозреваете, что это ноль.
Как использовать калькулятор нулей
Давайте обсудим, как использовать калькулятор нулей для нахождения нулей любой заданной функции.
Калькулятор нулей помогает легко найти нули любой функции. Найти нули любой функции можно и вручную, но это требует много времени и является очень длительной процедурой с точки зрения численных расчетов.
Рисунок-1 Методы поиска нулей
Таким образом, с помощью этого калькулятора вы можете шагнуть к желаемому результату с умом и сэкономить гораздо больше времени. Вам просто нужно выполнить эти простые шаги, чтобы найти нули любой функции.
Шаг 1:
Используйте калькулятор нуля , чтобы найти нули требуемой функции.
Шаг 2:
В калькуляторе есть вкладка выражения . Введите здесь функцию, для которой необходимо вычислить нули.
Шаг 3:
После того, как вы ввели функцию, для которой хотите найти нули, нажмите кнопку отправки , расположенную чуть ниже вкладки выражения.
Шаг 4:
После нажатия кнопки отправки перед вами появится новое окно с результатами. Калькулятор нулей находит нули заданной функции вместе с графиком корней, нулями, представленными на числовой прямой, суммой нулей и произведением нулей.
Шаг 5:
Наконец, для подробного и пошагового решения вам просто нужно нажать соответствующую кнопку, указанную для подробного решения, и вы можете просмотреть шаги.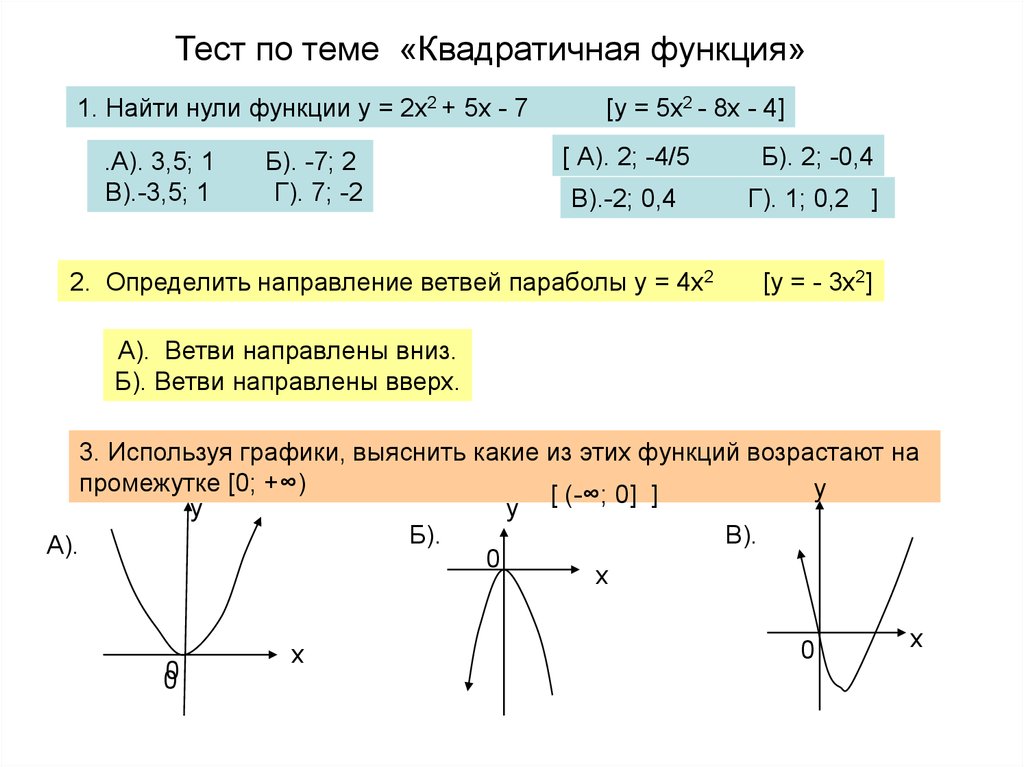
Как работает нулевой калькулятор?
A Калькулятор нулей работает, устанавливая функцию, эквивалентную нулю, и вычисляя нули. Он работает, выделяя переменную x на одной стороне уравнения или изменяя указанное уравнение несколько раз, чтобы найти все нули функции. Давайте углубимся в концепцию нулей функций.
Нахождение корней или нулей функций любого типа вручную очень трудоемко и чревато ошибками. Может быть многочлен с большим количеством корней, который вам почти невозможно вычислить вручную, но этот онлайн-калькулятор нулей поможет вам. Вы можете вычислить нули быстро, просто введя в него нужную функцию.
Что такое ноль функции?
ноль функции — это точка, соответствующая значениям переменной функции, которые при помещении в функцию становятся нулевыми. Графически нуль функции — это точка, в которой она пересекает ось абсцисс.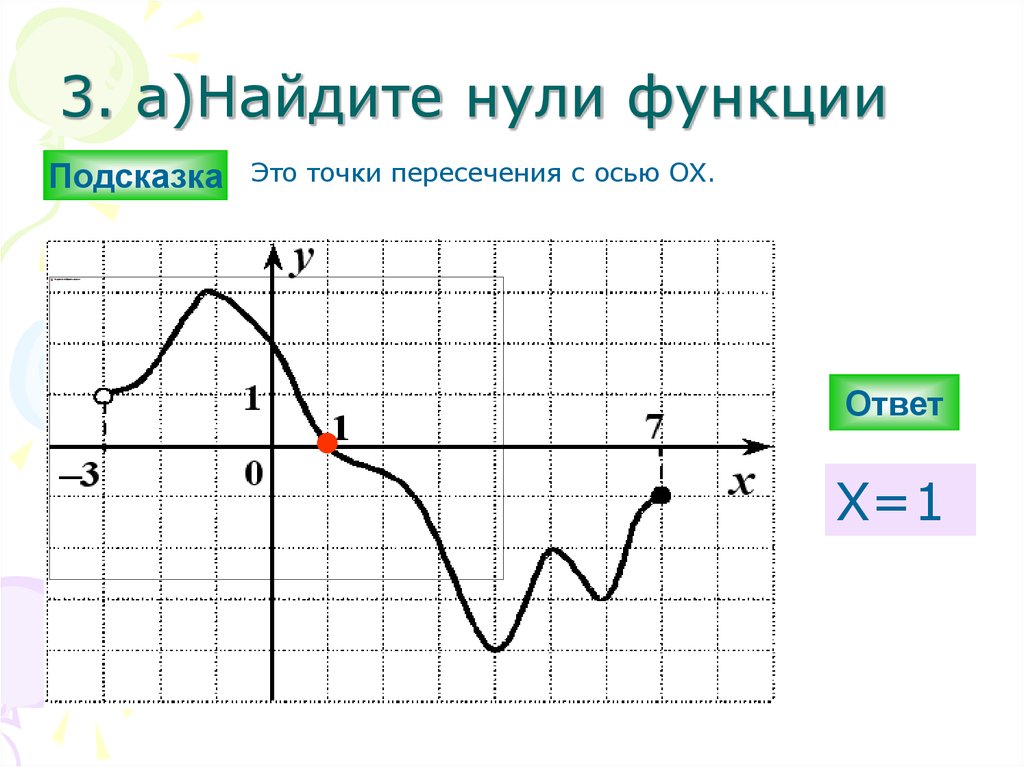
Чтобы найти значение нуля для данной функции, установите функцию равной нулю, а затем вычислите значение переменной функции; соответствующие значения называются нулями. Чтобы еще больше упростить концепцию, ноль функции определяется как точка, в которой функция становится равной нулю или пересекает ось x графика функции.
Еще одна важная вещь, которую следует учитывать, это то, что функция может иметь более одного нуля в зависимости от степени многочлена или функции. степень функции определяется как наивысшая степень ее переменной. Следовательно, общее количество нулей любой функции зависит от степени функции.
Например, чтобы еще больше прояснить эту концепцию, Линейная функция является функцией степени 1. Следовательно, все линейные функции имеют только один нуль. Аналогично, Квадратичная функция является функцией второй степени, поэтому все квадратичные функции имеют два нуля или пересекают ось абсцисс графика функции в двух точках.
Что такое настоящий ноль?
Нуль называется Вещественным нулем , если он принадлежит множеству действительных чисел при условии, что функция значения становится равной нулю. Если f(x) = 0, где x $in$ $mathbb{R}$, то x называется действительным нулем функции.
В чем разница между нулем и корнем?
Основное различие между нулем и корнем заключается в том, что ноль связан с функцией, тогда как корень относится к уравнению. ноль функции — это значение, при котором функция становится равной нулю, поскольку х называется корнем функции f(x) тогда и только тогда, когда f(x) становится равным нулю.
Корень уравнения — это значение его переменной x, при котором уравнение удовлетворяется или обе части уравнения становятся равными. Полиномиальное уравнение также может иметь более одного корня в зависимости от степени полиномиального уравнения.
Возможности калькулятора нулей
A Калькулятор нулей — очень полезный инструмент, так как он не только предоставляет вам корни функции, но также имеет некоторые дополнительные функции, перечисленные ниже:
Рис.
Корневой график
Корневой график — это графическое представление всех корней функции. На нем изображен график функции с указанием x-отрезков, являющихся нулями функции.
Номер Строка Представление
Калькулятор нулей также представляет нули функции на числовой прямой. Числовая линия определяется как линия, на которой через различные интервалы отмечены различные точки.
Сумма корней
Калькулятор нулей также позволяет вычислить сумму всех корней функции.
Произведение корней
Наконец, он также вычисляет произведение всех корней функции.
Решенные примеры
Пример 1:
Найдите корни заданной функции с помощью калькулятора нулей. Нарисуйте корневую диаграмму и числовое представление нулей. Также найдите сумму и произведение корней функции. 92-8 ]
Введите данную функцию на вкладке выражения калькулятора нулей.
Он отобразит следующие результаты:
Корни функции задаются как:
[ x = + 2 sqrt{2} ]
[ x = – 2 sqrt{2} ]
Корневой график показан на рисунке 1:
Рисунок 3.
Нули, представленные на числовой прямой, показаны на рисунке 2:
Рисунок 4. Нули функции четыре
Сумма всех корней:
сумма = 0
произведение = – 8
Пример 2:
Найдите нули следующей тригонометрической функции:
[ s f(x) = 2 qrt x +} ]
Используйте калькулятор, чтобы найти корни.
Введите заданную функцию на вкладке выражения калькулятора нулей, чтобы найти нули функции.
Он отобразит следующие результаты:
Корни функции даны как: 94 – 16 ]
Введите заданную функцию на вкладке выражения Калькулятора нулей, чтобы найти нули функции.
Эта полиномиальная функция имеет 4 корня (нули), так как это функция 4 степени. Он имеет два действительных корня и два комплексных корня
Результаты отобразятся в новом окне.
Корни функции задаются следующим образом:
x = + 2
x = – 2
x = + 2i
х = 902 + 8x + 35 ]
Используйте калькулятор, чтобы найти корни.
Введите заданную функцию на вкладке выражения калькулятора нулей, чтобы найти нули функции.
Это полиномиальная функция степени 4. Следовательно, она имеет четыре корня.
Все корни лежат в комплексной плоскости.
Корни функции задаются следующим образом:
x = -2 – i
x = -2 + i
[ x = 2 – iota sqrt{3} ]
[ x = 2 + iota sqrt{3} ]
Предыдущее
< Список математических калькуляторов > Следующее
Все изображения созданы с помощью Geogebr
Онлайн-заметки Пола
Главная
/
Алгебра
/
Полиномиальные функции
/ Нахождение нулей многочленов
Показать мобильное уведомление
Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
Раздел 5.4. Нахождение нулей многочленов
Мы говорили о нулях многочлена и зачем они нам сейчас в паре разделов. Мы, однако, толком не говорили о том, как на самом деле найти их для многочленов степени больше двух. Это тема этого раздела. Ну, это как раз тема этого раздела. Вообще, нахождение всех нулей любого многочлена — довольно сложный процесс. В этом разделе мы дадим процесс, который найдет все рациональные (, т.е. целых или дробных) нулей многочлена. Мы сможем использовать этот процесс для нахождения всех нулей полинома при условии, что все нули, кроме не более двух, рациональны.
Показать решение
Из факторизованной формы мы видим, что нули равны
[x = 4 = frac{4}{1}hspace{0,25 дюйма},,,x = frac{2}{3}hspace{0,25 дюйма}x = — frac{5} {4}]
Обратите внимание, что мы записали целое число в виде дроби, чтобы оно соответствовало теореме. Кроме того, с отрицательным нулем мы можем поставить минус в числителе или знаменателе. Это не имеет значения.
Итак, согласно теореме о рациональном корне, все числители этих дробей (со знаком минус в третьем нуле или без него) должны быть множителями 40, а знаменатели должны быть множителями 12.
Вот несколько способов размножить 40 и 12.
[begin{align*}40 & = left( 4 right)left( {10} right) & hspace{0.
Из них мы видим, что на самом деле все числители представляют собой множители 40, а знаменатели все множители 12. Также обратите внимание, что, как показано, мы можем поставить знак минус перед третьим нулем как в числителе, так и в знаменателе. и это все равно будет множитель соответствующего числа.
Чем же так полезна эта теорема? Ну, для начала это позволит нам записать список из возможных рациональных нулей для многочлена и, что более важно, любые рациональные нули многочлена БУДУТ в этом списке. 92} — 17x + 6) Показать решение
Что же говорит теорема о рациональном корне? В нем говорится, что если (x = frac{b}{c}) должно быть нулем (Pleft( x right)), то (b) должно быть множителем 6 и (c) должен быть множителем 1.
Итак, первое, что нужно сделать, это составить список всех возможных множителей 1 и 6. Вот они.
[begin{align*}6 & : pm 1,,, pm 2,,, pm 3,,, pm 6\ 1 & : pm 1end{align *}]
Теперь, чтобы получить список возможных рациональных нулей многочлена, все, что нам нужно сделать, это записать все возможные дроби, которые мы можем составить из этих чисел, где числители должны быть делителями 6, а знаменатели должны быть делителями 1. На самом деле это проще, чем может показаться на первый взгляд.
Есть очень простой сокращенный способ сделать это. Давайте подробно рассмотрим первый, а остальные сделаем быстрее. Во-первых, возьмите первый множитель из списка числителя, включая (pm), и разделите его на первый множитель (хорошо, в данном случае только множитель) из списка знаменателя, снова включая (pm ) .
[frac{{ pm 1}}{{ pm 1}}]
Похоже на беспорядок, но не так уж и плохо. Здесь четыре дроби. Они есть,
[frac{{ + 1}}{{ + 1}} = 1hspace{0,25 дюйма}frac{{ + 1}}{{ — 1}} = — 1hspace{0,25 дюйма}frac{ { — 1}}{{ + 1}} = — 1hspace{0,25 дюйма}frac{{ — 1}}{{ — 1}} = 1]
Однако обратите внимание, что все четыре дроби сводятся к двум возможным числам. Это всегда будет происходить с такими фракциями. Что мы будем делать с этого момента, так это формировать дробь, делать любые упрощения чисел, игнорируя ( pm ), а затем отбрасывать один из (pm ).
Итак, список возможных рациональных нулей для этого полинома:
[frac{{ pm 1}}{{ pm 1}} = pm 1hspace{0,25 дюйма}frac{{ pm 2}}{{ pm 1}} = pm 2hspace {0.25in}frac{{ pm 3}}{{ pm 1}} = pm 3hspace{0.
Получается, что возможных рациональных нулей всего 8, и в данном случае все они целые. Заметим также, что любые рациональные нули этого многочлена БУДУТ находиться где-то в этом списке, хотя мы их еще не нашли. 92} + 3x — 9) Показать решение
Мы не будем вдаваться в подробности. Сначала получите список всех делителей -9 и 2. Обратите внимание, что знак минус на 9 на самом деле не так уж важен, поскольку мы все равно получим (pm ) для каждого из факторов.
[begin{align*} — 9 & : pm 1,,, pm 3,,, pm 9\ 2 & : pm 1,,, pm 2end{ выровнять*}]
Теперь множители -9 — это все возможные числители, а множители 2 — все возможные знаменатели.
Вот список всех возможных рациональных нулей этого многочлена.
[begin{align*}frac{{ pm 1}}{{ pm 1}} & = pm 1 & hspace{0.
Итак, всего у нас есть 12 возможных рациональных нулей, половина из них — целые числа, а половина — дроби.
Следующий факт также иногда будет полезен при нахождении нулей полинома.
Факт
Если (Pleft( x right)) является полиномом и мы знаем, что (Pleft( a right) > 0) и (Pleft( b right) <0), то где-то между (a) и (b) находится ноль (Pleft( x right)).
Этот факт говорит нам о том, что если мы оцениваем многочлен в двух точках и одна из оценок дает положительное значение ( т.е. точка выше оси (х)), а другая оценка дает отрицательное значение ( т.е. точка ниже оси (х)), то единственный способ получить из одного точка на другую должна пройти через ось (x).
Обратите внимание, что этот факт не говорит нам, что такое ноль, он только говорит нам, что единица будет существовать. Также обратите внимание, что если обе оценки положительные или обе оценки отрицательные, между ними может быть или не быть ноль.
Вот процесс определения всех рациональных нулей многочлена.
Процесс поиска рациональных нулей
- Используйте теорему о рациональных корнях для получения списка всех возможных рациональных нулей многочлена (Pleft( x right)).
- Вычисляем многочлен по числам с первого шага, пока не найдем ноль. Предположим, что ноль равен (x = r), тогда мы будем знать, что это ноль, потому что (Pleft( r right) = 0). После того, как было установлено, что это на самом деле нуль, запишите исходный многочлен как
[Pвлево( x вправо) = влево( {x — r} вправо)Qвлево( x вправо)] - Повторите процесс, используя (Qleft( x right)) на этот раз вместо (Pleft( x right)).
Это повторение будет продолжаться до тех пор, пока мы не достигнем полинома второй степени. На данный момент мы можем решить это непосредственно для оставшихся нулей.
Для упрощения второго шага воспользуемся синтетическим делением. Это значительно упростит нашу жизнь в нескольких отношениях. Во-первых, напомним, что последнее число в последней строке — это многочлен, оцененный в (r), и если мы получим ноль, оставшиеся числа в последней строке — это коэффициенты для (Qleft( x right) ), и поэтому нам не придется возвращаться и находить это. 92} — 17х + 6).
Показать решение
В предыдущем примере мы нашли список всех возможных рациональных нулей. Они здесь.
[ pm 1,,, pm 2,,, pm 3,,, pm 6]
Теперь нам нужно начать вычисление многочлена для этих чисел. Мы можем начать с любого места в списке и будем продолжать, пока не найдем ноль.
Для оценки мы построим синтетическая таблица деления . В синтетической таблице деления выполняем умножение в уме и опускаем среднюю строку, просто записывая третью строку, и, поскольку мы будем проходить этот процесс несколько раз, мы помещаем все строки в таблицу.
Вот первая синтетическая таблица деления для этой задачи.
[begin{массив}{г|ррррл}
{} & 1 & -7 & 17 & -17 & 6 \ hline
-1 & 1 & -8 & 25 & -42 & 48=Pleft(-1 right)ne 0 \
1 & 1 & -6 & 11 & -6 & 0=Pleft( 1 right)=0,,!,,!
конец{массив}]
Итак, мы нашли ноль. Прежде чем перейти к этому, давайте повторим вычисления здесь, чтобы убедиться, что вы можете их выполнить.
Верхняя строка — это коэффициенты полинома, а первый столбец — это числа, по которым мы оцениваем полином.
Каждая строка (после первой) является третьей строкой процесса синтетического деления.
[ pm 1,,, pm 2,,, pm 3,,, pm 6]
Теперь, перед созданием новой синтетической таблицы деления, давайте вспомним, что мы ищем нули в (Pleft( x right)) и из нашей первой таблицы деления мы определили, что (x = — 1) равно НЕ является нулем (Pleft( x right)), и поэтому нет причин снова возиться с этим числом.
Это то, что мы всегда должны делать на этом этапе. Взгляните на список новых возможных рациональных нулей и спросите, есть ли такие, которые не могут быть рациональными нулями исходного многочлена. Если они есть, выбросьте их, так как мы уже знаем, что они не будут работать. Итак, сокращенный список чисел, которые можно попробовать здесь, 9.0005
[1,,, pm 2,,, pm 3,,, pm 6]
Обратите внимание, что нам необходимо включить (x = 1) в список, поскольку ноль может встречаться более одного раза (, т.е. кратность больше единицы).
Вот синтетическая таблица деления этого многочлена.
[begin{массив}{r|rrrl}
{} & 1 & -6 & 11 & -6 \ hline
1 & 1 & -5 & 6 & ,,0=Pleft( 1 right)=0!! \
конец{массив}]
92} — 5x + 6 = left( {x — 2} right)left( {x — 3} right) = 0hspace{0.
Обратите внимание, что эти два числа находятся в списке возможных рациональных нулей.
Завершение этой задачи дает следующий список нулей для (Pleft( x right)).
[ begin{align*}& x = 1hspace{0,25in}left( {{mbox{кратность 2}}} right)\ & x = 2hspace{0,25in}left({ {mbox{кратность 1}}} right)\ & x = 3hspace{0,25 дюйма}left( {{mbox{кратность 1}}} right)end{align*}]
92} + 3х — 9).
Показать решение
Из второго примера мы знаем, что список всех возможных рациональных нулей равен
.
[begin{align*}frac{{ pm 1}}{{ pm 1}} & = pm 1 & hspace{0.25in}frac{{ pm 3}}{{ pm 1 }} & = pm 3 & hspace{0.25in}frac{{ pm 9}}{{ pm 1}} & = pm 9\ & \ frac{{ pm 1}}{ { pm 2}} & = pm frac{1}{2} & hspace{0,25in}frac{{ pm 3}}{{ pm 2}} & = pm frac{3} {2} & hspace{0,25 дюйма}frac{{ pm 9}}{{ pm 2}} & = pm frac{9}{2}end{align*}]
Следующим шагом является создание синтетической таблицы деления.
[begin{массив}{г|ррррл}
{} и 2 и 1 и 3 и 3 и -9\ hline
-9 & 2 & -17 & 156 & -1401 & 12600=Pleft(-9 right)ne 0 \
-3 & 2 & -5 & 18 & -51 & 144=Pleft(-3 right)ne 0 \
-1 & 2 & -1 & 4 & -1 & -8=Pleft(-1 right)ne 0 \
конец{массив}]
Теперь мы еще не нашли ноль, однако заметим, что (Pleft( { — 3} right) = 144 > 0) и (Pleft( -1 right)=- 8
[begin{массив}{г|ррррр}
{} & 2 & ,,1 & 3 & ,,3 & -92} + 6х — 6]
Теперь нам нужно повторить весь процесс с этим полиномом. Кроме того, в отличие от предыдущего примера, мы не можем просто повторно использовать исходный список, поскольку на этот раз последнее число отличается.
[begin{align*} — 6 & : pm 1,,, pm 2,,, pm 3,,, pm 6\ 2 & : pm 1,, , pm 2end{выравнивание*}]
Вот список всех возможных рациональных нулей для (Qleft( x right)).
[begin{align*}frac{{ pm 1}}{{ pm 1}} & = pm 1 & hspace{0.25in}frac{{ pm 2}}{{ pm 1 }} & = pm 2 & hspace{0.25in}frac{{ pm 3}}{{ pm 1}} & = pm 3 &hspace{0.25in}frac{{ pm 6} }{{ pm 1}} & = pm 6\ & \ frac{{ pm 1}}{{ pm 2}} & = pm frac{1}{2} & hspace{ 0.25in}frac{{ pm 2}}{{ pm 2}} & = pm 1& hspace{0.25in}frac{{ pm 3}}{{ pm 2}} & = pm frac{3}{2} & hspace{0,25 дюйма}frac{{ pm 6}}{{ pm 2}} & = pm 3end{align*}]
Обратите внимание, что некоторые числа появляются в обеих строках, поэтому мы можем сократить список, записав их только один раз.
Нули функции
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
Примеры.
1) Найти нули линейной функции y=3x+15.
Решение:
Чтобы найти нули функции, решим уравнение 3x+15=0.
3x=-15; x= -5.
Таким образом, нуль функции y=3x+15 — x= -5.
Ответ:x= -5.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Решение:
Для нахождения нулей функции решим квадратное уравнение
x²-7x+12=0.
Его корни x1=3 и x2=4 являются нулями данной функции.
Ответ: x=3; x=4.
3)Найти нули функции
Решение:
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0,x²≠1,x≠±1. То есть область определения данной функции (ОДЗ)
x ∈ (-∞; -1)U(-1; 1)U(1;∞).
Решаем уравнение
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Ответ: x=-4.
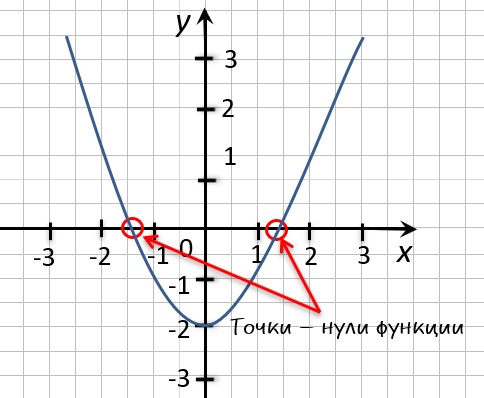
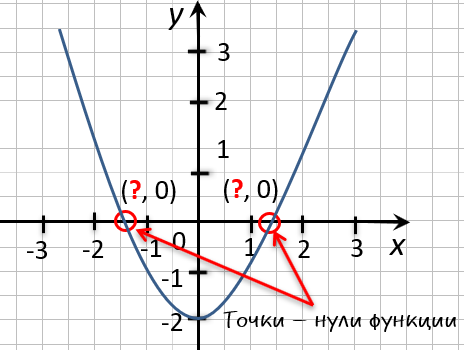
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
Например,
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.






 Это повторение будет продолжаться до тех пор, пока мы не достигнем полинома второй степени. На данный момент мы можем решить это непосредственно для оставшихся нулей.
Это повторение будет продолжаться до тех пор, пока мы не достигнем полинома второй степени. На данный момент мы можем решить это непосредственно для оставшихся нулей. 

