Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Запомните!
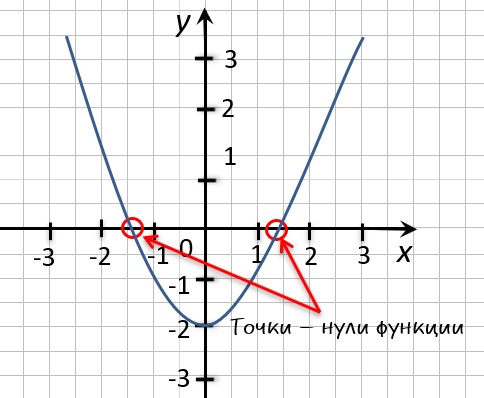
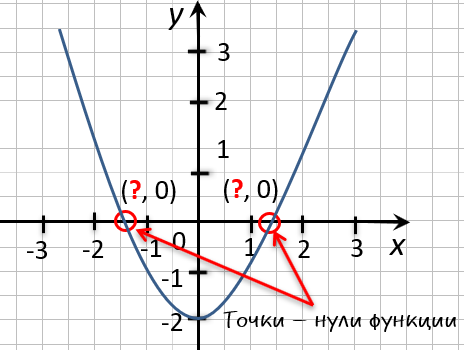
Нули функции — это
значения « x »
(аргумента функции),
при которых « y = 0 ».
В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу
(аналитически). Разберем алгоритм решения
подобных задач.
Как найти нули функции, заданной формулой
Важно!
Чтобы найти нули функции, нужно:
- в формулу функции вместо
« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»; - решить полученное уравнение
относительно « x »; - записать полученные решения уравнения для « x » в ответ.
По традиции разберемся на примере.
Разбор примера
Найдите нули функции:
Подставим вместо значения функции « f(x) » ноль.
0 = 0,2x + 3
Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».
Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.
−0,2x = 3 | · (−1)
0,2x = −3
Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.
0,2x = −3
· x = −3 | · 10
· x · 10 = −3 · 10
· x = −30
2x = −30
x =
x = −15
Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3
Разбор примера
Найдите нули функции:
Вместо « f(x) » подставим ноль.
0 = x 3 − 4x
−x 3 + 4x = 0 | · (−1)
(−1) · (−x 3 + 4x) = 0 · (−1)
x 3 − 4x = 0
Вынесем общий множитель
« x » за скобки.
В левой части полученного уравнения у нас два множителя:
« x »
и «(x 2 − 4)». Результат их умножения равен нулю.
Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x 2 − 4)»
равен нулю.
Решаем квадратное уравнение
«x 2 − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − 4 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.
Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x 3 − 4x
Разбор примера
Найдите нули функции:
Подставим вместо « h(x) » ноль.
Перенесем правую часть
в левую, изменив ее знак на минус.
Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x 2 − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.
Решим полученное квадратное уравнение через формулу с дискриминантом.
a · x 2 + b · x + c = 0
x1;2 =
x 2 − x − 6 = 0
x1;2 =
| −(−1) ± √(−1)2 − 4 · 1 · (−6) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −2 |
Ответ: x = −2; x = 3 являются нулями функции
h(x) =
Разбор примера
Найдите нули функции:
Заменим «f(x)» на ноль.
Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x 2 − 4 = 0 »
будет равен нулю, когда его подкоренное выражение
« x 2 − 4 »
будет равно нулю.
Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x 2 − 4».
x1;2 =
x 2 − 4 = 0
x1;2 =
| −(−0) ± √(−0)2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x 2 − 4
Как найти нули функции на графике функции
Важно!
Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).
По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.
Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».
Рассмотрим на примере.
Разбор примера
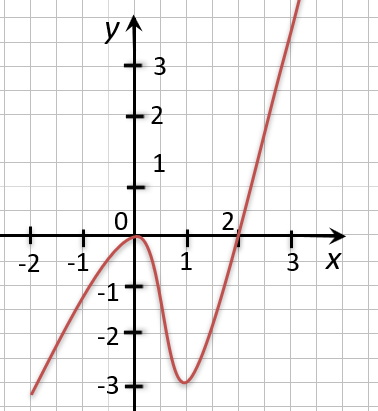
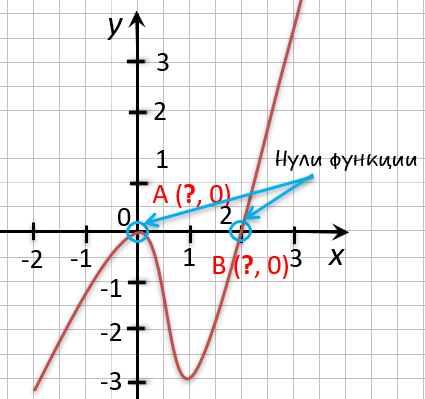
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.
Отметим на графике функции его точки пересечения с осью « Ox ».
Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось
« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.
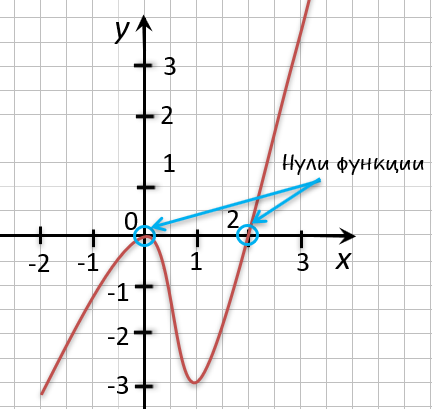
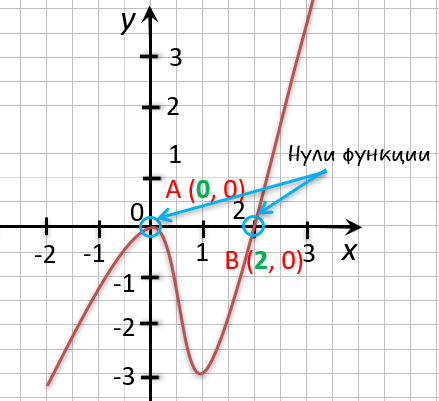
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».
Запишем полученные значения координат « x » в ответ.
Ответ: x = 0; x = 2 являются нулями функции.
Как найти нули функции, заданной таблицей
В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.
Разбор примера
Найдите нули функции, заданной таблицей.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Вспомним определение нулей функции.
Запомните!
Нули функции — это
значения « x » в функции,
при которых « y = 0 ».
Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −3 | −1,5 | 0 | 2 | 1 | 0 |
Остаётся только записать в ответ значения « x » из таблицы.
Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Как найти нули функции по уравнению с дробью?
У = дробь в числителе х ^ 2 – 6х + 5 ; в знаменателе х – 5 Объясните пожалуйста!
На странице вопроса Как найти нули функции по уравнению с дробью? из категории Алгебра вы найдете
ответ для уровня учащихся 5 – 9 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.
Анализ дробно-рациональной функции. Асимптоты, экстремум
Функция $y=frac{k}{x}$ . Гипербола. Свойства.
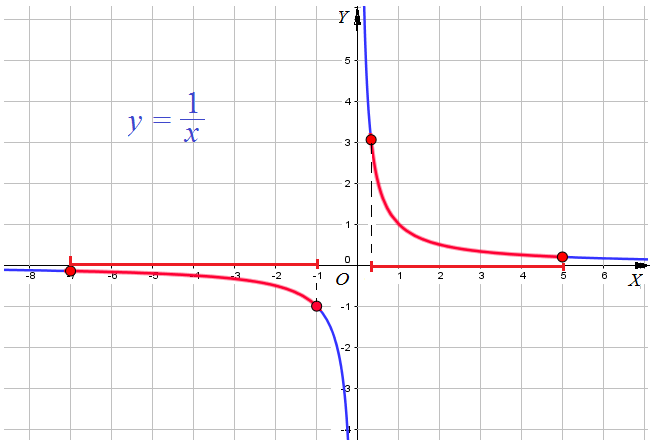
Пример 1: Построить график для функции $y=frac{1}{x}$, $fleft(xright)=frac{1}{x}$
- Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
- $fleft(1right)=1$ $fleft(frac{1}{2}right)=2$ $fleft(-1right)=-1$ $x=-frac{1}{2}$ $fleft(-frac{1}{2}right)=-2$ $fleft(2right)=frac{1}{2}$ $fleft(frac{1}{4}right)=4$ $fleft(-frac{1}{4}right)=-4$ $fleft(4right)=frac{1}{4}$ $fleft(1right)=8$ $fleft(-4right)=-frac{1}{4}$ $fleft(-frac{1}{8}right)=-8$ .
- Точки Графика $(1;1)$, $(2;1/2)$, $(4;1/4)$, $(1/2;2)$, $(1/4;4)$, $(1/8;8)$, $(-1;-1)$, $(-2;-1/2)$, Еще точки: $(-4;-1/4)$, $(-1/2;-2)$, $(-1/4;-4)$, $(-1/8;-8)$ . По всем точкам построим кривые – график функции $y=frac{1}{x}$
- График имеет разрыв по вертикальной линии $x=0$. Ветви графика прижимаются к горизонтальной линии $y=0$.
Графиком функции $y=frac{k}{x}$ $kne0$ является гипербола , ветви прижимаются к асимптотическим линиям.
- если коэффициент $k > 0$ , в I и III координатных четвертях. Точка $(0;0)$ – центр симметрии.
- если $k < 0$ , то во II и IV координатных четвертях. Точка $(0;0)$ – центр симметрии.
- Асимптоты: Вертикальная асимптота, линия $x=0$, Горизонтальная асимптота, линия $y=0$
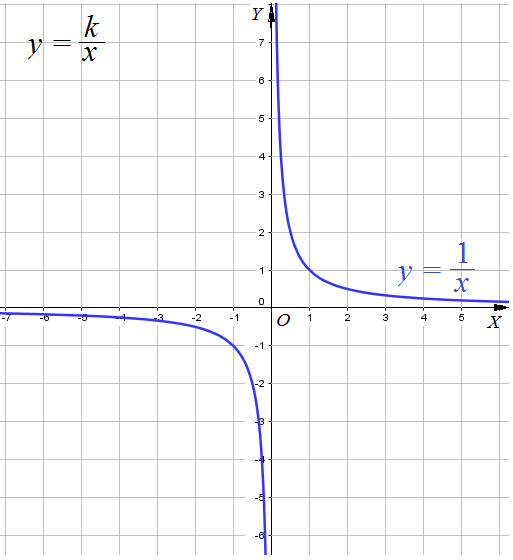
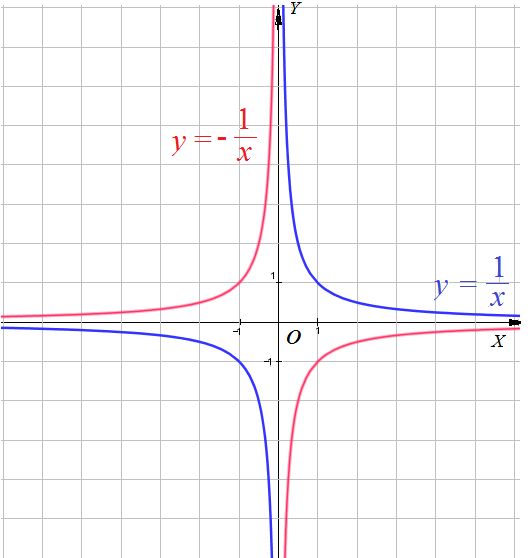
Cвойства функции $y=frac{k}{x}$ при $k > 0$ ( ветви гиперболы расположены в первом и третьем координатных углах) .
Свойство 1: Область Определения Функции – вся числовая прямая , кроме $x=0$. Свойство 2: $y > 0$ при $x > 0$; $y < 0$ при $x < 0$. Свойство 3: Функция убывает на промежутках $( – ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 4: Функция не ограничена ни снизу, ни сверху. Свойство 5: Ни наименьшего, ни наибольшего значений $у$ у функций нет. Свойство 6: Функция непрерывна на $( – ∞ ; 0 )$ и $( 0 ; + ∞)$. Свойство 7: Область значений функции – $( – ∞ ; 0 )$ U $( 0 ; + ∞)$. имеет разрыв в точке $x=0$.
Cвойства функции $y=frac{k}{x}$ при $k < 0$ (ветви гиперболы расположены во втором и четвертом координатных углах).
Свойство 1: Область Определения Функции – вся числовая прямая , кроме $x=0$. Свойство 2: $y > 0$ при $x < 0$ ; $y < 0$ при $x > 0$. Свойство 3: Функция возрастает на промежутках $( – ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 4: Функция не ограничена ни снизу, ни сверху. Свойство 5: Ни наименьшего, ни наибольшего значений $у$ у функций нет. Свойство 6: Функция непрерывна на $( – ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 7: Область значений функции – объединение $( – ∞ ; 0 )$ U $( 0 ; + ∞)$ . имеет разрыв в точке $x=0$.
Метод Замены для построения Графика Функции.
Мысль: Умеем строить график функции попроще … используем его для построения функции при “сдвинутых” аргументах и значениях.
Как построить график функции $y=kcdot fleft(xright)$, если известен график функции $y=fleft(xright)$.
- График $y=5cdot fleft(xright)$: Расстянуть вертикально вверх по оси $OY$ 5 раз все, что над $OX$ графика $y=fleft(xright)$ , $k$ раза.
- График $y=5cdot fleft(xright)$: Расстянуть вертикально вниз по оси $OY$ 5 раз все, что под $OX$ графика $y=fleft(xright)$ , $k$ раза.
- График $y=frac{1}{3}cdot fleft(xright)$: Сжать по вертикали, оси $OY$ график $y=fleft(xright)$ 3 раза.
- Еще способ: Перемасштабирование. Для $y=5cdot fleft(xright)$ … построить $y=fleft(xright)$, изменить масштаб: “1” станет “5”, “-2” станет “-10”, и т.д.
Как построить график функции $y=-fleft(xright)$, если известен график функции $y=fleft(xright)$.
- Эти функции принимают ровно противоположные значения. Значит: график $y=fleft(xright)$ надо отразить по оси $OX$, “перевернуть”.
Как построить график функции $y=fleft(x+lright)$, если известен график функции $y=fleft(xright)$.
- Построить график $y=fleft(x+lright)$, где $l > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба влево.
- Построить график $y=fleft(x-lright)$, где $l < 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба вправо.
Как построить график функции $y=fleft(xright)+m$, если известен график функции $y=fleft(xright)$.
- Построить график $y=fleft(xright)+m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вверх;
- Построить график $y=fleft(xright)-m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вниз.
Как построить график функции $y=fleft(x+lright)+m$, если известен график функции $y=fleft(xright)$.
- График функции $y=fleft(x+lright)+m$ можно получить из графика $y=fleft(xright)$ параллельными сдвигами по осям $OX$ и $OY$.
График Дробной Функции.
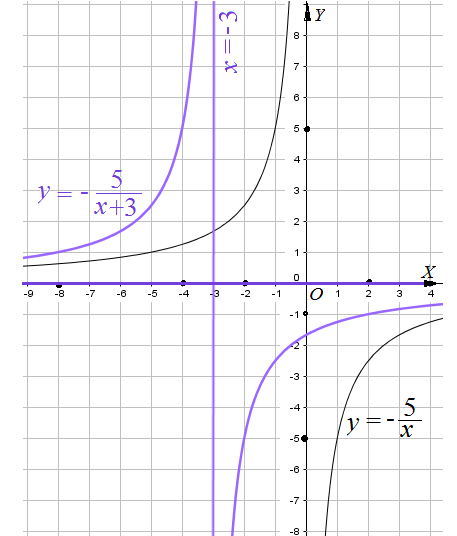
Пример 2: Построить график функции $y=-frac{5}{x+3}$ .
- сначала построим график функции $y=-frac{5}{x}$ … от графика $y=frac{1}{x}$ … отразим от $OX$ и растянем по вертикали 5 раз.
- сдвинем получившуюся гиперболу вдоль оси $OX$ на $3$ единицы влево, получится требуемый график.
- это гипербола с асимптотами $x=-3$; $y=0$. “почему так?” – как мы строим графики?
- берем несколько $x$ – точек и находим для каждого свои $y$ – значения в соответствии “с формулой функции”.
- По точкам проводим график. Очевидно, если, скажем, $x=0,52$ функция $y=-frac{5}{x+3}$ дает какое-то значение,
- … то, конечно для $x=3,52$ другая функция, $y=-frac{5}{x}$ дает ровно такое же значение.
- значит, точки графиков будут различаться на $3$ единицы по $x$ – координате и совпадать по $y$ – координате.
- Ровно так и для всех точек. “Сравни две функции и вообрази их графики: каковы различия и что общего? “
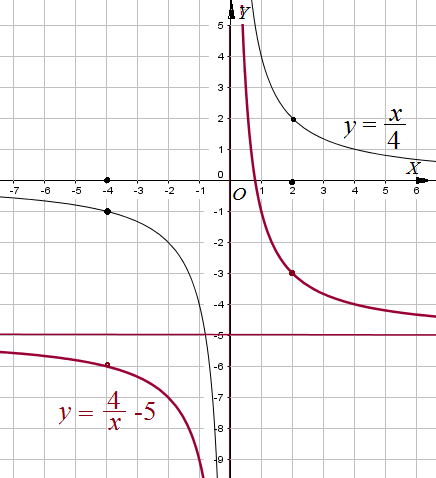
Пример 3: Построить график функции $y=frac{4}{x}-5$ .
- Сначала надо построить график функции $y=frac{4}{x}$ . Гиперболу $y=frac{1}{x}$ “растянем” четыре раза.
- Сдвинуть получившуюся гиперболу вдоль оси $OY$ на $5$ клеточек вниз. Т.к. каждое значение должно отличаться на 5 единиц.
- получится требуемый график. Это гипербола с асимптотами $x=0$; $y=-5$.
- Важно знать где пересекается с нулем. Решение, корень $frac{4}{x}-5=0$ дает абсциссу $x=0.8$. Точка графика $left(0,8;0right)$.
- Исследование: Найдем производное: $left(frac{4}{x}-5right)’=-frac{4}{x^2}$. Нигде не = 0, Экстремума нет!
- Производная для всех $x$ (кроме $0$) отрицательна – значит всюду убывает.
- Область Определения: $D_f=left(-infty;0right)+left(0;+inftyright)$ Область значений $E_f=left(-infty; -5right)+left(-5;+inftyright)$
- Знакопостоянство: $+Z_f=left(-infty;0,8right)$ – функция отрицательна, $-Z_f=left(0,8;+inftyright)$ – функция положительна.
- Монотонность: $+M_f=left(-infty;-3right)+left(-3;0right)$ – возрастает $-M_f=left(0;3right)+left(3;+inftyright)$ – функция убывает
Вертикальная асимптота ( $x=0$,) проходит в полюсе, точке разрыва функции. Точка обнуления знаменателя. Параллельно $OY$.
Горизонтальная асисмптота ( $y=-5$ ), линия, на которую “ложится” график при значениях $х$ около $+-infty$. Параллельно $OX$.
Гипербола – график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы “зажаты – прижаты” к асимптотическим линиям .
Наклонная асимптота – линия типа $y=2x+3$, к которой “прижимаются” ветви графика “на” или “около” + – бесконечнoсти.
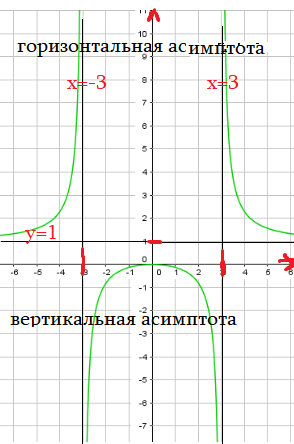
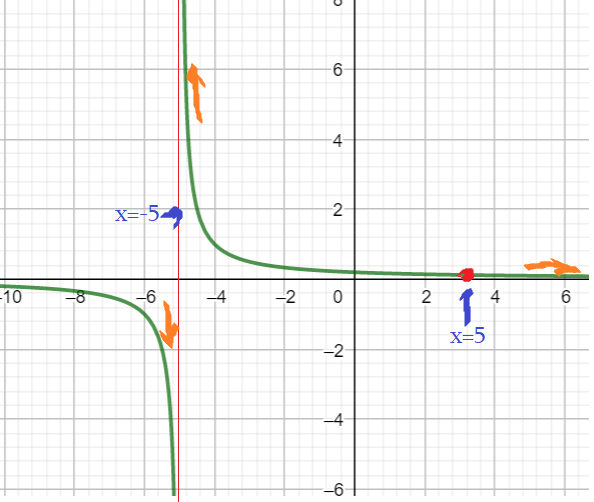
Пример 4: Построить график функции $y=frac{x-5}{x^2-25}$
- Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
- Тождественное преобразование, сокращение $frac{x-5}{x^2-25}=frac{x-5}{(x+5)(x-5)}=frac{1}{x+5}$. Так, что график $y=frac{1}{x+5}$ ?
- Не спеши! Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З – в исходной функции нет места $x=5$.
- Значит: можем строить гиперболу $y=frac{1}{x+5}$ взамен нашей $y=frac{x-5}{x^2-25}$, но “без точки $x=5$”.
- Точка $x=5$ разрывает “гладкий” график гиперболы. Она называется “выколотая точка с координатами $left(5;0,1right)$”.
Важно уметь исследовать функцию – график около точек разрыва. + / – поблизости. Куда тянется?
- Исследуем около $x=-5$. Возьмем “близкие” точки $-5,01$ и $-4,99$. Вычислим приближенные значения.
- Чуть левее … $fleft(-5,01right)=frac{-5,01-5}{(-5,01)^2-5^2}approx -100$. Чуть правее … $fleft(-4,99right)=frac{-4,99-5}{(-4,99)^2-5^2}approx 100$.
- Прямая $x=-5$ – вертикальная асимптота. Ветвь слева прижимается “вниз”, к $-infty$ . А справа поднимается вверх к $+infty$.
- Около $x=5$. Чуть левее $fleft(4,99right)=frac{4,99-5}{4,99^2-5^2}approx0,101$. $fleft(5,01right)=frac{5,01-5}{5,01^2-5^2}approx0,099$.
- Значит, $x=5$ точка разрыва, на графике выколотая точка $left(5;0,1right)$. Т.к. в ней $y=frac{1}{5+5}=0,1$.
- “О нулях”: при $x=0$ $y=0,2$ . Но функция нигде не обнуляется, $yne0$. Прямая $y=0$ – горизонтальная асимптота.
- Анализ: Найдем производное: $left(frac{x-5}{x^2-25}right)’=left(frac{1}{x+5}right)’=-frac{1}{left(x+5right)^2}$
- Производная не равна нулю нигде и всюду отрицательна. Экстремума нет, Всюду убывающая функция.
- Область Определения функции: $D_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$ .
- Знакопостоянство: $+Z_f=left(-5;5right)+left(5;+inftyright)$ – функция положительна. $-Z_f=left(-infty;-5right)$ – функция отрицательна
- Монотонность: $+M_f=varnothing $ – нет роста. $-M_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$ – функция убывает
- Область значений $E_f=left(-infty;0right)+left(0;0,8right)+left(0,8;inftyright)$
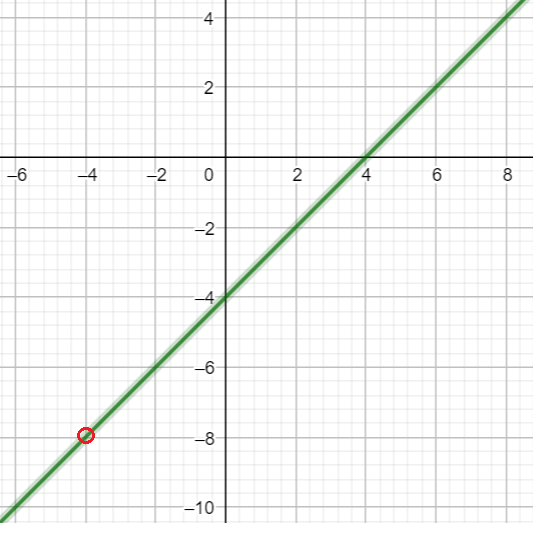
Пример 5: Построить график функции $y=frac{x^2-16}{x+4}$
- О.Д.З функции $xne-4$. Оговорив это, со спокойной совестью сократим $y=frac{x^2-16}{x+4}=x-4$.
- График нашей функции – прямая линия $y=x-4$ с выколотой точкой $left(-4;-8right)$ при $x=-4$.
- “Близко чуть левее”: $x=-4,01$ значение $fleft(-4,01right)=frac{(-4,01)^2-16}{-4,01+4}=-8,01$. Ближе? … Предел $approx-8$.
- “О нулях”. при $x=0$ $y=-4$ . Обнуление функции $y=0$ при $x=4$ – пересечение с $x$ – осью.
- Анализ: Найдем производное: $left(frac{x^2-16}{x+4}right)’=left(x-4right)’=1$
- Производное всюду равно 1. Постоянный рост. Кроме разрыва, конечно. Нет точки Экстремума.
- Область Определения: $D_f=left(-infty;-4right)+left(4;+inftyright)$ Область значений $E_f=left(-infty;-8right)+left(-8;inftyright)$
- Знакопостоянство: $+Z_f=left(4;+inftyright)$ – функция положительна. $-Z_f=left(-infty;4right)$ – функция отрицательна
- Монотонность: $+M_f=left(-infty;-4right)+left(-4;inftyright)$ – возрастает
График Дробно – Рациональной Функции.
Определение: дробно-рациональной порядка $left(n;mright)$ называется функция вида $y=frac{acdot x^n+5x^3-x+c}{bcdot x^m-4x^2-7x+d}$
Числитель – многочлен степени $n$ , знаменатель – многочлен степени $m$ . Общий вид: $y=frac{Pleft(xright)}{Qleft(xright)}$
Нули функции – корни числителя $Pleft(xright)=0$ , Асимптоты (полюсы) – корни знаменателя $Qleft(xright)=0$.
Пример 6: Построить график функции $y=frac{x^2}{x^2-9}$.
- Функция $fleft(xright)=frac{x^2}{x^2-9}$ – четная: $fleft(xright)=fleft(xright)$ $fleft(8right)=fleft(-8right)$ – Слева и справа от $OY$ симметрично.
- Вычисления: $fleft(-4right)=frac{left(-4right)^2}{left(-4right)^2-9}=frac{16}{7}approx2,3$ $fleft(-10right)=frac{100}{91}approx 1,1$ $fleft(-5right)=frac{25}{16}approx 1,6$ $fleft(-3,5right)=frac{12.25}{3,25}approx 3,8$
- $fleft(-2right)=fleft(2right)=frac{4}{-5}approx -0,8$ $fleft(-1right)=fleft(1right)approx -0,1$ $fleft(3,5right)approx 3,8$ $fleft(4right)approx 2,3$ $fleft(5right)approx 1,6$ $fleft(10right)approx 1,1$
- Наша функция имеет нули в точке $x=0$ , а вертикальные асимтоты – линии $x=-3$ , $x=3$
- Асимптота – прямая линия, к которой “прижимается” график функции, “подходя” к ней бесконечно близко.
- Чему равно $frac{x^2}{x^2-9}$ при очень больших $x$ ? $xapproxpm1000$ ? Конечно, $yapprox1$ горизонтальная асимптота $y=1$ .
- Анализ графика: 1) Обнуляется при $x=0$ . 2) Значение в нуле : $y=frac{x^2}{x^2-9}$ в $x=0$ равно $y=0$.
- 3) Поведение в разрывах: “чуть левее” полюса $xapprox-3-0,01$ значение $y > 0$ – “большое положительное”.
- “чуть правее” разрыва $xapprox-3+0,01$ значение функции “большое отрицательное”.
- Поведение около другого разрыва: когда $x$ “чуть левее” , например $xapprox3-0,01$ , то $y < 0$ ;
- когда $x$ “чуть правее” , например $xapprox3+0,01$ , то $y > 0$.
- 4) Поведение на бесконечности: при $xapproxpminfty$ значение “ложится” около $yapprox1$.
- 5) Область определения функции – все точки оси $x$ , кроме $x=pm3$
- 6) Функция положительна $y > 0$ на интервалах $x < -3$ , $x > 3$.
- 7) Функция отрицательна $y < 0$ на интервалах $-3 < x < 0$ , $0 < x < 3$.
Исследование Функции:
- Найдем производное: $left(frac{x^2}{x^2-9}right)’=frac{2xleft(x^2-9right)-x^2cdot2x}{left(x^2-9right)^2}=frac{-18x}{left(x^2-9right)^2}$
- Производное равно нулю дает точку Экстремума: $x=0$. Точка Максимума.
- Производная отрицательна – значит убывает $x > 0$. Производная положительна, значит возрастает: $x < 0$
- Область Определения: $D_f=left(-infty;-3right)+left(-3;3right)+left(3;+infty8right)$ – область определения функции.
- Знакопостоянство: $+Z_f=left(-infty;-3right)+left(3;+inftyright)$ – функция положительна. $-Z_f=left(-3;3right)$ – функция отрицательна
- Монотонность: $+M_f=left(-infty;-3right)+left(-3;0right)$ – возрастает $-M_f=left(0;3right)+left(3;+inftyright)$ – функция убывает
- Область значений $E_f=left(-infty;0right)+left(1;inftyright)$
пробaп 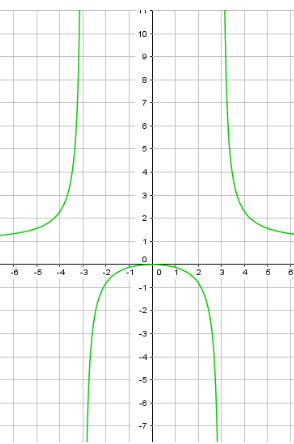
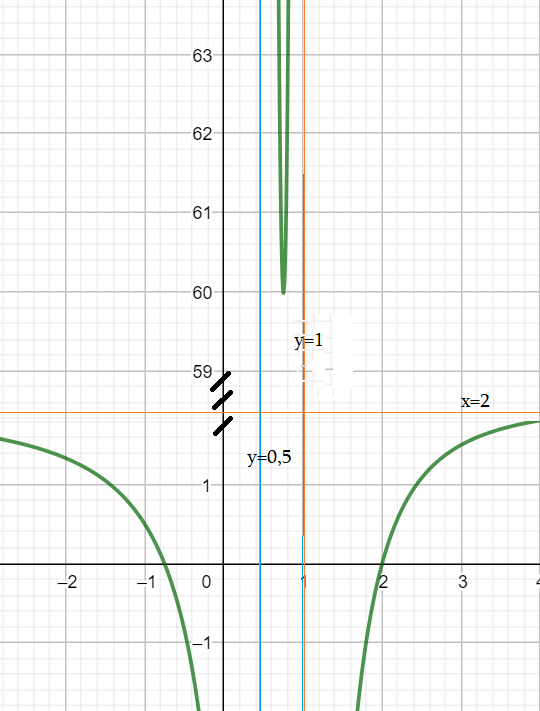
Пример 7: Анализ графика функции $y=frac{4x^2-5x-6}{2x^2-3x+1}$
- нули – точки обнуления числителя $4x^2-5x-6=0$ $x=2$ $x=-frac{3}{4}$
- Представление: $frac{4x^2-5x-6}{2x^2-3x+1}=frac{2cdot left(2x^2-3x+1right)+x-8}{2x^2-3x+1}=2+frac{x-8}{2x^2-3x+1}=2+frac{x-8}{left(2x-1right)left(x-1right)}=2+frac{15}{2x-1}-frac{7}{x-1}$
- разрыв (полюс): $2x^2-3x+1=0$ вертикальные асимптоты – $x=1$ и $x=0,5$.
- при $xapproxpm infty$ значение “ложится” около $yapprox2$. $-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}$ $x=0,75$ $x=15,24$
- Производное: $left(2+frac{15}{2x-1}-frac{7}{x-1}right)’=-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}=frac{-2x^2+32x-23}{left(2x-1right)^2cdotleft(x-1right)^2}$
- Или так: $left(frac{4x^2-5x-6}{2x^2-3x+1}right)’=frac{left(4x^2-5x-6right)’cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(2x^2-3x+1right)’}{left(2x^2-3x+1right)^2}=frac{left(8x-5right)cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(4x-3right)}{left(2x^2-3x+1right)^2}=frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}$
- Уравнение Экстремумов: $frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}=0$. $-2x^2+32x-23=0$. $x=8pm0,5sqrt{210}$
- Производная отрицательна на интервалах $-M_f=left(-infty;0,5right)+left(0,5;8-0,5sqrt{210}right)+left(8+0,5sqrt{210};inftyright)$. Убывает.
- Производная положительна на интервалах $+M_f=left(8-0,5sqrt{210};1right)+left(1;8+0,5sqrt{210}right)$. Возрастает.
- Точка Минимума: $x=8-0,5sqrt{210}$ $xapprox0,75$ . Точка Максимума: $x=8+0,5sqrt{210}$ $xapprox15,25$
- Область Определения: $D_f=left(-infty;0,5right)+left(0,5;1right)+left(1;+inftyright)$ .
- Знакопостоянство: $+Z_f=left(-infty;-0,75right)+left(0,5;1right)+left(2;+inftyright)$ – положительна. $-Z_f=left(-0,75;0right)+left(1;2right)$ – отрицательна.
- Область значений (приближенно!) $E_fapproxleft(-infty;2,001right)+left(60;inftyright)$
Пример 8: Анализ графика функции $y=frac{3x^2-5x-8}{x-2}$
- нули – точки обнуления числителя $3x^2-5x+8=0$ $x=-1$ $x=frac{8}{3}approx2,7$
- разрыв (полюс): $x-2=0$ вертикальные асимптоты – $x=2$ .
- “чуть левее”: $fleft(2-10^{-7}right)=frac{3cdotleft(2-10^{-7}right)^2-5left(2-10^{-7}right)-8}{2-10^{-7}-2}=frac{3cdot4-5cdot2-8-12cdot10^{-7}+5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{-10^{-7}}approx6cdot10^7$ Значит, уходит к $+infty$
- Чуть правее: $fleft(2+10^{-7}right)=frac{3cdotleft(2+10^{-7}right)^2-5left(2+10^{-7}right)-8}{2+10^{-7}-2}=frac{3cdot4-5cdot2-8+12cdot10^{-7}-5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{10^{-7}}approx-6cdot10^7$ …. бежит к $-infty$
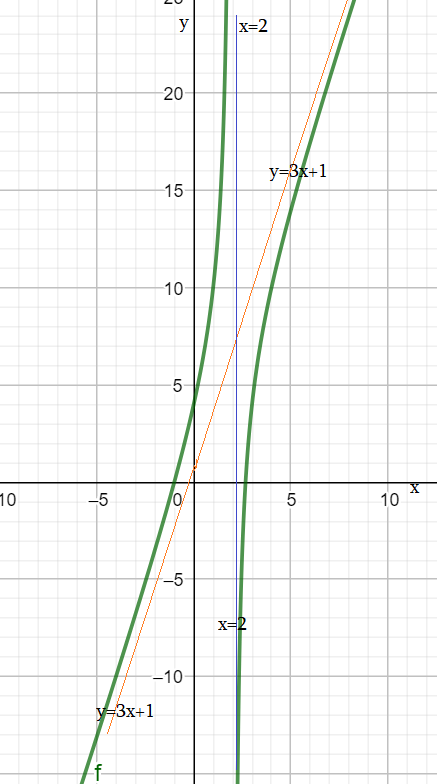
- Представим нашу функцию по-другому : $frac{3x^2-5x-8}{x-2}=frac{3x^2-6x+x-2-6}{x-2}=3x+1-frac{6}{x-2}$
- Видно, что при больших $x=2$ она “почти совпадает” с линейной функцией $3x+1$. “прижимается к ней”.
- $y=3x+1$ – наклонная асимптота нашей функции.
- Найдем производное: $left(frac{3x^2-5x-8}{x-2}right)’=frac{left(6x-5right)left(x-2right)-1cdotleft(3x^2-5x-8right)}{(x-2)^2}=frac{3x^2-12x+18}{(x-2)^2}=frac{3left(x^2-4x+6right)}{(x-2)^2}$
- Производное нигде не равно нулю, нет Экстремума: Производное всюду положительно, значит, возрастает.
- Область Определения: $D_f=left(-infty;2right)+left(2;+inftyright)$ . Полюс в $x=2$ .
- Знакопостоянство: $+Z_f=left(-1;2right)+left(frac{8}{3};+inftyright)$ – функция положительна. $-Z_f=left(-infty;-1right)+left(-1;frac{8}{3}right)$ – функция отрицательна
- Монотонность: $+M_f=left(-infty;2right)+left(2;inftyright)$ – всюду возрастает
- Область значений $E_f=left(-infty;+inftyright)$
Графический способ решения уравнений
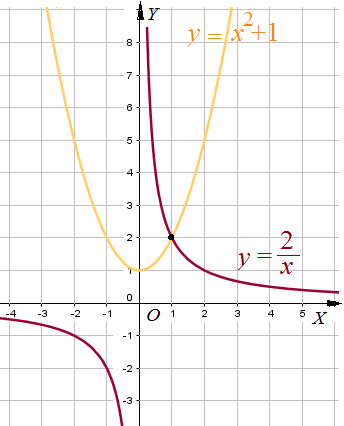
Пример 9: Решить уравнение $frac{2}{x}=x^2+1$ графическим способом.
- Построим гиперболу $y=frac{2}{x}$ и параболу $y=x^2+1$ . Равенство означает пересечение.
- Левая функция и правая функция приобретают одинаковые значения … графики этих функций пересекаются.
- По чертежу видно, что графики пересекаются в точке с координатами $left(1;2right)$. ответ: $x=1$.
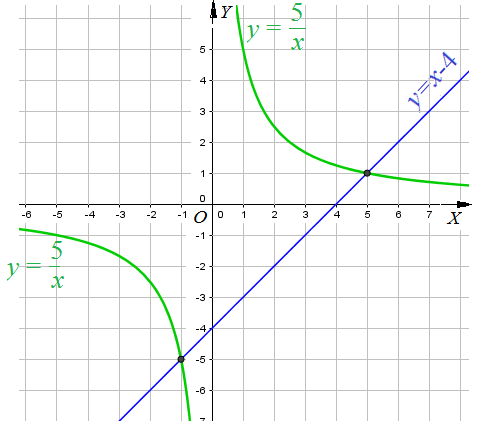
Пример 10: Решить уравнение $frac{5}{x}=x-4$.
- Построим их графики: гиперболу $y=frac{5}{x}$ и прямую $y=x-4$. пересекаются ?
- Гипербола и прямая пересекаются в точках $(-1;-5)$ и $(5;1)$. ответ: $x_1=-1$; $x_2=5$.
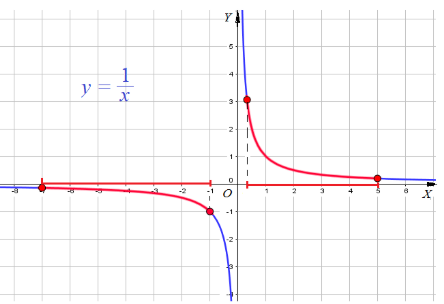
Пример 11: Найти наименьшее и наибольшее значения функции $y=frac{1}{x}$ на отрезках а) $left[frac{1}{3};5right]$ и б) $left[-7;-1right]$.
- Построим график функции $y=frac{1}{x}$ .
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[frac{1}{3};5right]$.
- Для выделенной части графика находим: наименьшее значение $y=frac{1}{5}$ при $x=5$ , наибольшее $y=3$ при $x=frac{1}{3}$.
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[-7;-1right]$.
- Для выделенной части графика находим: наименьшее значение $y=-frac{1}{7}$ при $x=-7$ наибольшее $y=-1$ при $x=-1$.
Упражнения
- Главная
- Алгебра
- как найти нули …
-
Предмет:
Алгебра
-
Автор:
rigobertofrye
-
Создано:
3 года назад
Ответы 2
Заметим, что знаменатель дроби не может равняться нулю, x ≠ 5.
График функции пересекает прямую y = 0, поэтому приравнивая функции , мы найдем нули функции
По теореме Виета:
– не нуль функции (так как это выколотая точка)
-
Автор:
elmo
-
Оценить ответ:
0
Ответ:
решение представлено на фото
Объяснение:
-
Автор:
londyn
-
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
-
Музыка19 минут назад
9) Распределите определения по жанрам: кантата, марш, концерт, этюд, песня, опера, балет, прелюдия, вокализ, романс, оратория, баркарола, оперетта
1.ВОКАЛЬНЫЕ ЖАНРЫ:
2.ИНСТРУМЕНТАЛЬНЫЕ ЖАНРЫ:
3.СИНТЕТИЧЕСКИЕ ЖАНРЫ:
Заранее спасибо если поможете
-
Физика3 часа назад
Оценить число молекул воздуха в земной атмосфере, если давление воздуха вблизи поверхности Земли на уровне моря равно 760 мм рт.ст., молярная масса воздуха 29 г/моль. Радиус Земли 6400 км. Ускорение свободного падения считать постоянным и равным 9,8 м/с2 .
-
Математика4 часа назад
умоляю помогите
-
Математика6 часов назад
Помогите пожалуйста от этой оценки зависит годовая оценка
-
Информатика14 часов назад
3 вариант
-
Информатика14 часов назад
Помогите
-
Физика17 часов назад
Реохорд. какая электрическая величина меняется в цепи при изменении длины включенного реохорда
-
Математика18 часов назад
Представить в виде степенного ряда решение дифференциального уравнения, удовлетворяющее данным начальным условиям (для уравнения пер- вого порядка найти четыре ненулевых члена ряда, для уравнения второго по- рядка – пять членов).
y”=ye^x+1 y(0)=2; y'(0)=1.
-
Математика18 часов назад
1. Случайная величина распределена равномерно на отрезке [−2; 5]. Найти математическое ожидание и дисперсию. Что вероятнее: в результате ис- пытания случайная величина окажется в интервале (2,5; 3) или вне его?
-
Математика18 часов назад
1. В цехе работают 8 мужчин и 12 женщин. По табельным номерам отбира- ют 6 человек. Какова вероятность того, что среди них будут только 2 женщины?
-
Физика18 часов назад
определи фокусное расстояние лупы с точностью до сантиметра если её оптическая сила равна d 5.3 дптр.
-
Алгебра20 часов назад
-6x^2+x+2>0.Решение квадратных неравенств
-
Физика20 часов назад
2.3. Блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы а = 30° и (3 = 45°. Гири равной массы
(т
х = т2 = 2 кг) соединены нитью, перекинутой через блок. Считая нить и блок невесомыми, принимая коэффициенты трения гирь о наклонные плоскости равными f1= f2= =0,1 и пренебрегая трением в блоке, определите: 1) ускорение, с которым движутся гири; 2) силу натяжения нити. [1) 0,24 м/с2; 2) 12 Н]
-
История1 день назад
ПЖ помогите КТО ЭТО Я НЕЗНАЮ
-
Алгебра1 день назад
Негр и мексиканец падают с небоскрёба. Кто упадёт первым?
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

hiz65ndm1
+20
Решено
8 лет назад
Алгебра
5 – 9 классы
как найти нули функции по уравнению с дробью?
у= дробь в числителе х^2 – 6х + 5 ; в знаменателе х – 5
Объясните пожалуйста!!!
Смотреть ответ
2
Ответ проверен экспертом
3
(3 оценки)
3
triolana
3 года назад
Светило науки – 553134 ответа – 388270 раз оказано помощи
Заметим, что знаменатель дроби не может равняться нулю, x ≠ 5.
График функции пересекает прямую y = 0, поэтому приравнивая функции , мы найдем нули функции
По теореме Виета:
– не нуль функции (так как это выколотая точка)
(3 оценки)
Ответ проверен экспертом
5
(2 оценки)
2
lilyatomach
3 года назад
Светило науки – 2214 ответов – 15243 помощи
Ответ:
решение представлено на фото
Объяснение:

(2 оценки)
https://vashotvet.com/task/6848765