|
|
Макеты страниц
Ц. р.ф. или многочлен можно рассматривать не только при действительных значениях  но и при любых комплексных значениях
но и при любых комплексных значениях  ; в самом деле, все действия, необходимые для получения значения многочлена
; в самом деле, все действия, необходимые для получения значения многочлена

имеют смысл при любом комплексном  (мы сохраним обозначение
(мы сохраним обозначение  для действительной части
для действительной части  Разумеется, при этом и значения, принимаемые многочленом, будут, вообще говоря, комплексными числами. Однако вполне возможно, что при некоторых комплексных (мнимых) значениях z многочлен не только будет иметь действительные значения, но может обращаться в нуль. В дальнейшем, в гл. V, изучая алгебраические уравнения, мы будем искать все их корни, а не только действительные. Поэтому полезно сейчас рассмотреть вопрос о значениях многочлена
Разумеется, при этом и значения, принимаемые многочленом, будут, вообще говоря, комплексными числами. Однако вполне возможно, что при некоторых комплексных (мнимых) значениях z многочлен не только будет иметь действительные значения, но может обращаться в нуль. В дальнейшем, в гл. V, изучая алгебраические уравнения, мы будем искать все их корни, а не только действительные. Поэтому полезно сейчас рассмотреть вопрос о значениях многочлена  при комплексных значениях
при комплексных значениях  .
.
Даламбером была сделана попытка доказать, а Гауссом окончательно доказано важное предложение:
Всякий многочлен степени  имеет в комплексной области хотя бы один корень.
имеет в комплексной области хотя бы один корень.
Это предложение, устанавливающее существование корня многочлена (быть может, не действительного), носит название основной теоремы алгебры. Теорема эта верна даже и для многочленов с комплексными коэффициентами, но мы ограничиваемся только случаем многочленов с действительными коэффициентами. Доказательства теоремы Гаусса мы привести не можем.
В п. 15, говоря о комплексно сопряженных числах, мы отметили, что сумма, разность, произведение чисел, комплексно сопряженных с данными, комплексно сопряжены, соответственно, с их суммой, разностью, произведением.
Отсюда вытекает утверждение:
Значения многочлена (52.1) при комплексно сопряженных значениях  сопряжены между собой.
сопряжены между собой.
Доказательство. Значения  выражаемые равенствами
выражаемые равенствами

будут сопряжены, так как получаются одинаковыми действиями над сопряженными числами. В самом деле,  -действительные коэффициенты, и они, следовательно, сами себе сопряжены:
-действительные коэффициенты, и они, следовательно, сами себе сопряжены:  Поэтому можно написать
Поэтому можно написать

и из сравнения  получим
получим 
Следствие. Если многочлен  имеет комплексный корень
имеет комплексный корень  , то и сопряженное число
, то и сопряженное число  является его корнем.
является его корнем. 
В самом деле, если  , то
, то  . Пусть теперь а — действительный корень многочлена (52.1). По теореме Безу разделим
. Пусть теперь а — действительный корень многочлена (52.1). По теореме Безу разделим  на
на  и напишем
и напишем

Если  , то многочлен
, то многочлен  также обязан иметь корень. Может случиться, что число а снова является его корнем. Тогда повторим деление
также обязан иметь корень. Может случиться, что число а снова является его корнем. Тогда повторим деление  на
на  и получим
и получим

Пусть, вообще говоря, деление на  нацело удается выполнить k раз, но уже не удается в
нацело удается выполнить k раз, но уже не удается в  раз. Тогда а мы называем
раз. Тогда а мы называем  – кратным корнем многочлена
– кратным корнем многочлена  и пишем
и пишем

Многочлен  здесь уже не делится на
здесь уже не делится на  нацело. Если
нацело. Если  то корень а называется однократным или простым; если
то корень а называется однократным или простым; если  корень называется кратным.
корень называется кратным.
Может быть, многочлен  также имеет действительный корень
также имеет действительный корень  (кратности
(кратности  ). Тогда мы напишем
). Тогда мы напишем

и продолжим этот процесс до исчерпания всех действительных корней  Если при этом в записи
Если при этом в записи

 и, следовательно, последний множитель
и, следовательно, последний множитель  то процесс привел нас к отысканию всех корней многочлена и разложению многочлена на линейные множители. Сравнение степеней даст нам при этом
то процесс привел нас к отысканию всех корней многочлена и разложению многочлена на линейные множители. Сравнение степеней даст нам при этом

т. е. сумма кратностей корней равна степени многочлена. Говорят проще, что многочлен имеет столько корней, какова его степень (считая каждый кратный корень столько раз, какова его кратность).
Может, однако случиться, что на некотором шаге в записи (52.2) многочлен положительной степени  Уже не имеет ни одного действительного корня. Тогда, в силу основной теоремы алгебры, он имеет комплексный корень
Уже не имеет ни одного действительного корня. Тогда, в силу основной теоремы алгебры, он имеет комплексный корень  Вместе с тем он имеет и корень а
Вместе с тем он имеет и корень а  Нетрудно было бы распространить теорему Безу и на случай деления на двучлен
Нетрудно было бы распространить теорему Безу и на случай деления на двучлен  с мнимым а. Многочлен должен делиться поэтому на
с мнимым а. Многочлен должен делиться поэтому на  и на
и на  Для того чтобы не вводить эти мнимые сомножители в разложение многочлена на множители, можно, вместо последовательного выполнения деления на
Для того чтобы не вводить эти мнимые сомножители в разложение многочлена на множители, можно, вместо последовательного выполнения деления на  разделить
разделить  сразу на произведение
сразу на произведение

которое уже оказывается квадратным трехчленом с действительными коэффициентами (и отрицательным дискриминантом:  . В результате в записи разложения
. В результате в записи разложения  на множители появятся множители вида
на множители появятся множители вида  (снова однократные или повторяющиеся):
(снова однократные или повторяющиеся):

где последнее частное  – число. Сравнение коэффициента при
– число. Сравнение коэффициента при  в левой и правой частях равенства (52.2) покажет, что
в левой и правой частях равенства (52.2) покажет, что  . Поэтому окончательно разложение многочлена с действительными коэффициентами на действительные множители имеет вид
. Поэтому окончательно разложение многочлена с действительными коэффициентами на действительные множители имеет вид

Вывод: многочлен с действительными коэффициентами разлагается в произведение (повторяющихся или нет) линейных двучленов вида  и квадратных трехчленов вида
и квадратных трехчленов вида  . Число всех корней многочлена с учетом их кратности равно его степени
. Число всех корней многочлена с учетом их кратности равно его степени  .
.
Пример. Число  является корнем многочлена
является корнем многочлена

Указать кратность корня  и разложить
и разложить  на множители
на множители
Решение. Применяя схему Горнера для деления многочлена на  (можно обойтись и без схемы Горнера, выполнив деление обычным способом, как в п. 50):
(можно обойтись и без схемы Горнера, выполнив деление обычным способом, как в п. 50):

Таким образом, частное равно  :
:

Многочлен, найденный как частное от деления, снова делим на 

Получаем частное  и еще раз делим его на
и еще раз делим его на 

Теперь остаток отличен от нуля, поэтому окончательно

где  уже не делится на
уже не делится на  без остатка. Корень
без остатка. Корень  – двукратный корень многочлена. Трехчлен
– двукратный корень многочлена. Трехчлен  имеет комплексно сопряженные корни (см. п. 59), так как его дискриминант отрицателен:
имеет комплексно сопряженные корни (см. п. 59), так как его дискриминант отрицателен:  Разложение на множители, записанное в форме (52.4), имеет вид
Разложение на множители, записанное в форме (52.4), имеет вид

Упражнения
1. Разделить многочлен  на многочлен
на многочлен  найти частное
найти частное  и остаток
и остаток 
2. Проверить, делится или не делится многочлен  на двучлен:
на двучлен: 
3. Определить коэффициенты а и б многочлена  если известно, что он без остатка делится на двучлен
если известно, что он без остатка делится на двучлен  при делении на двучлен
при делении на двучлен  дает остаток, равный 6.
дает остаток, равный 6.
4. Многочлен  имеет корень
имеет корень  Какова кратность этого корня? Разложить многочлен на множители.
Какова кратность этого корня? Разложить многочлен на множители.
Оглавление
- ВВЕДЕНИЕ
- Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
- 2. Простые и составные числа. Признаки делимости.
- 3. Наибольший общий делитель и наименьшее общее кратное.
- 4. Целые числа. Рациональные числа.
- 5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
- 6. Иррациональные числа. Действительные числа.
- 7. Действия с приближенными числами.
- 8. Числовая ось. Координаты точки на плоскости.
- § 2. Степени и корни
- 9. Степени с натуральными показателями.
- 10. Степени с целыми показателями.
- 11. Корни.
- 12. Степени с рациональными показателями. Степени с действительными показателями.
- 13. Алгоритм извлечения квадратного корня.
- § 3. Комплексные числа
- 14. Основные понятия и определения.
- 15. Рациональные действия с комплексными числами.
- 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
- 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.
- 18. Извлечение корня из комплексного числа.
- Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
- 19. Алгебраические выражения. Одночлены и многочлены.
- 20. Формулы сокращенного умножения.
- 21. Бином Ньютона.
- 22. Разложение многочлена на множители.
- 23. Дробные алгебраические выражения.
- § 2. Иррациональные алгебраические выражения
- 24. Радикалы из алгебраических выражений.
- 25. Освобождение от иррациональности в знаменателе дроби.
- Глава III. ЛОГАРИФМЫ
- 26. Определение и свойства логарифмов.
- 27. Логарифмы по различным основаниям. Модуль перехода.
- § 2. Десятичные логарифмы
- 28. Характеристика и мантисса десятичного логарифма.
- 29. Применение десятичных логарифмов к вычислениям.
- Глава IV. ФУНКЦИИ И ГРАФИКИ
- 30. Величина. Числовые множества.
- 31. Определение функции.
- 32. График функции. Способы задания функций.
- 33. Элементарное исследование поведения функции.
- 34. Сложная функция.
- 35. Обратная функция.
- 36. Функции нескольких переменных.
- § 2. Элементарные функции
- 37. Обзор элементарных функций.
- 38. Линейная функция.
- 39. Квадратичная функция у=ах^2.
- 40. Степенная функция у = х^n.
- 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
- 42. Показательная функция.
- 43. Логарифмическая функция.
- § 3. Преобразование графиков
- 44. Параллельный сдвиг графика.
- 45. График квадратного трех члена.
- 46. График дробно-линейной функции.
- 47. Преобразование симметрии. Сжатие и растяжение графика.
- 48. Построение графиков функций.
- 49. Сложение графиков.
- § 4. Некоторые сведения о рациональных функциях
- 50. Целые и дробные рациональные функции. Деление многочленов.
- 51. Схема Горнера. Теорема Безу.
- 52. Нули многочлена. Разложение многочлена на множители.
- Глава V. УРАВНЕНИЯ
- 53. Уравнение. Корни уравнения.
- 54. Равносильные уравнения.
- 55. Системы уравнений.
- 56. Графическое решение уравнений.
- §. 2. Алгебраические уравнения с одной неизвестной
- 57. Число и кратность корней.
- 58. Уравнения первой степени (линейные уравнения).
- 59. Уравнения второй степени (квадратные уравнения).
- 60. Формулы Виета. Разложение квадратного трехчлена на множители.
- 61. Исследование квадратного уравнения.
- 62. Уравнения высших степеней. Целые корни.
- 63. Двучленные уравнения.
- 64. Уравнения, сводящиеся к квадратным.
- 65. Возвратные уравнения.
- § 3. Системы алгебраических уравнений
- 66. Линейные системы.
- 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
- 68. Системы, состоящие из уравнения второй степени и линейного уравнения.
- 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
- § 4. Иррациональные, показательные и логарифмические уравнения
- 70. Иррациональные уравнения.
- 71. Показательные уравнения.
- 72. Логарифмические уравнения.
- 73. Разные уравнения. Системы уравнений.
- Глава VI. НЕРАВЕНСТВА
- 74. Свойства неравенств. Действия над неравенствами.
- 75. Алгебраические неравенства.
- § 2. Решение неравенств
- 76. Множество решений неравенства. Равносильные неравенства.
- 77. Графическое решение неравенств.
- 79. Квадратные неравенства.
- 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
- 81. Иррациональные, показательные и логарифмические неравенства.
- 82. Неравенства с двумя неизвестными.
- Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
- 83. Числовая последовательность.
- 84. Предел числовой последовательности.
- 85. Бесконечно малые. Правила предельного перехода.
- § 2. Арифметическая прогрессия
- 86. Арифметическая прогрессия. Формула общего члена.
- 87. Свойства арифметической прогрессии.
- 88. Формула для суммы n членов арифметической прогрессии.
- § 3. Геометрическая прогрессия
- 89. Геометрическая прогрессия. Формула общего члена.
- 90. Свойства геометрической прогрессии.
- 91. Формулы для суммы n членов геометрической прогрессии.
- 92. Бесконечно убывающая геометрическая прогрессия.
- Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
- 93. Вектор, проекция вектора.
- 94. Положительные углы и дуги, меньшие 360°.
- 95. Углы и дуги, большие 360°.
- 96. Отрицательные углы. Сложение и вычитание углов.
- § 2. Тригонометрические функции произвольного угла
- 97. Определение основных тригонометрических функций.
- 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
- § 3. Соотношения между тригонометрическими функциями одного и того же угла
- 99. Основные тригонометрические тождества.
- 100. Вычисление значений тригонометрических функций по значению одной из них.
- 101. Значения тригонометрических функций некоторых углов.
- § 4. Четность, нечетность и периодичность тригонометрических функций
- 102. Четность и нечетность.
- 103. Понятие периодической функции.
- 104. Периодичность тригонометрических функций.
- § 5. Формулы приведения
- 105. Зависимость между тригонометрическими функциями дополнительных углов.
- 106. Формулы приведения.
- Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
- § 1. Тригонометрические функции числового аргумента
- 108. Области определения и области изменения значений тригонометрических функций.
- 109. Некоторые неравенства и их следствия.
- § 2. Графики тригонометрических функций
- 110. Первоначальные сведения о таблицах тригонометрических функций.
- 111. Основные графики.
- 112. Примеры построения графиков некоторых других тригонометрических функций.
- 113. Дальнейшие примеры построения графиков функций.
- Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
- 114. Расстояние между двумя точками на плоскости.
- 115. Косинус суммы и разности двух аргументов.
- 116. Синус суммы и разности двух аргументов.
- 117. Тангенс суммы и разности двух аргументов.
- 118. О формулах сложения для нескольких аргументов.
- § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
- 119. Тригонометрические функции двойного аргумента.
- 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.
- 121. Тригонометрические функции половинного аргумента.
- 122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
- § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
- § 4. Преобразование в произведение сумм вида
- § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
- 127. Преобразование в произведение выражения a•sina + b•cosa.
- 128. Преобразование в произведение выражений a•sina+b и a•cosa+b
- 129. Преобразование в произведение выражения a•tga+b.
- Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
- 130. Функция у = arcsin x (арксинус).
- 131. Функция y = arccos x (арккосинус).
- 132. Функция y = arctg x (арктангенс).
- 133. Функция y = arcctg x (арккотангенс).
- 134. Пример.
- § 2. Операции над обратными тригонометрическими функциями
- 135. Тригонометрические операции.
- 136. Операции сложения (вычитания).
- § 3. Обратные тригонометрические операции над тригонометрическими функциями
- 137. Функция у = arcsin (sin x).
- 138. Функция y = arctg (tg x).
- Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- 139. Уравнение sin х = а.
- 140. Уравнение cos х = a.
- 141. Уравнение tg x = a.
- 142. Уравнение ctg x = a.
- 143. Некоторые дополнения.
- § 2. Способ приведения к одной функции одного и того же аргумента
- 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
- 146. Способ разложения на множители.
- 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
- § 3. Некоторые частные приемы решения тригонометрических уравнений и систем
- 148. Введение вспомогательного аргумента.
- 149. Преобразование произведения в сумму или разность.
- 150. Переход к функциям удвоенного аргумента.
- 151. Решение уравнения типа…
- 152. Применение подстановок sinx ± соsx = y.
- § 4. Решение тригонометрических неравенств
- 154. Простейшие тригонометрические неравенства.
- 155. Примеры тригонометрических неравенств, сводящихся к простейшим.
- Часть вторая. ГЕОМЕТРИЯ
- 156. Точка. Прямая. Луч. Отрезок.
- 157. Плоскость. Фигуры и тела.
- 160. Равенство фигур. Движение.
- 161. Равенство тел.
- § 2. Измерение геометрических величин
- 162. Сложение отрезков. Длина отрезка.
- 163. Общая мера двух отрезков.
- 164. Сравнительная длина отрезков и ломаных.
- 165. Измерение углов.
- 166. Радианная мера угла.
- 167. Измерение площадей.
- 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
- Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
- 169. Перпендикуляр и наклонные.
- 170. Свойство перпендикуляра, проведенного к отрезку в его середине.
- 171. Параллельные прямые.
- 172. Углы, образованные двумя параллельными прямыми и секущей.
- 173. Углы с параллельными или перпендикулярными сторонами.
- § 2. Геометрические места точек. Окружность
- 174. Геометрическое место точек.
- 175. Свойство биссектрисы угла.
- 176. Окружность.
- 177. Взаимное расположение прямой и окружности. Касательная и секущая.
- 178. Хорда и диаметр. Сектор и сегмент.
- 179. Взаимное расположение двух окружностей.
- § 3. Основные задачи на построение
- 181. Деление отрезка пополам. Построение перпендикуляров.
- 182. Построение углов.
- 183. Другие задачи на построение.
- Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
- 184. Стороны и углы треугольника.
- 185. Биссектрисы треугольника. Вписанная окружность.
- 186. Оси симметрии сторон треугольника. Описанная окружность.
- 187. Медианы и выcоты треугольника.
- 188. Равенство треугольников.
- 189. Построение треугольников.
- 190. Равнобедренные треугольники.
- 191. Прямоугольные треугольники.
- § 2. Параллелограммы
- 192. Четырехугольники.
- 193. Параллелограмм и его свойства.
- 194. Прямоугольник.
- § 3. Трапеция
- 196. Трапеция.
- 197. Средняя линия треугольника.
- 198. Средняя линия трапеции.
- 199. Деление отрезка на равные части.
- § 4. Площади треугольников и четырехугольников
- 200. Площадь параллелограмма.
- 201. Площадь треугольника.
- 202. Площадь трапеции.
- Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
- 203. Пропорциональные отрезки.
- 204. Свойства биссектрис внутреннего и внешнего углов треугольника.
- § 2. Подобное преобразование фигур (гомотетия)
- 205. Определение гомотетичных фигур.
- 206. Свойства преобразования подобия.
- § 3. Общее подобное соответствие фигур
- 207. Подобные фигуры.
- 208. Периметры и площади подобных треугольников.
- 209. Применение подобия к решению задач на построение.
- Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
- 210. Углы с вершиной на окружности.
- 211. Углы с вершиной внутри и вне круга.
- 212. Угол, под которым виден данный отрезок.
- 213. Четырехугольники, вписанные в окружность.
- 214. Пропорциональные отрезки в круге.
- 215. Задачи на построение.
- § 2. Метрические соотношения в треугольнике
- 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора.
- 218. Теорема синусов. Формула Герона.
- 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
- 218. Теорема синусов. Формула Герона.
- 219. Радиусы вписанной и описанной окружностей.
- § 3. Решение треугольников
- 220. Таблицы функций.
- 221. Решение треугольников. Сводка основных формул.
- 222. Решение прямоугольных треугольников.
- 223. Решение косоугольных треугольников.
- Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
- 224. Выпуклые многоугольники.
- 225. Правильные многоугольники.
- 226. Соотношения между стороной, радиусом и апофемой.
- 227. Периметр и площадь правильного n-угольника.
- 228. Удвоение числа сторон правильного многоугольника.
- § 2. Длина окружности. Площадь круга и его частей
- 229. Длина окружности.
- 230. Площадь круга и его частей.
- Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- 231. Взаимное расположение двух прямых в пространстве.
- 232. Взаимное расположение прямой линии и плоскости.
- 233. Взаимное расположение двух плоскостей.
- 234. Свойства параллельных прямых и плоскостей.
- 235. Построения в стереометрии.
- § 2. Перпендикулярность прямых и плоскостей
- 236. Перпендикуляр к плоскости.
- 237. Перпендикуляр и наклонные.
- 238. Угол между прямой и плоскостью.
- 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
- 240. Общий перпендикуляр двух скрещивающихся прямых.
- § 3. Двугранные и многогранные углы
- 241. Двугранный угол.
- 242. Взаимно перпендикулярные плоскости.
- 243. Трехгранные углы.
- 244. Многогранные углы.
- § 4. Многогранники
- 245. Многогранники.
- 246. Правильные многогранники.
- Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
- 247. Цилиндры и призмы.
- 248. Параллелепипеды.
- 249. Объемы призм и цилиндров.
- 250. Площадь боковой поверхности призмы.
- 251. Площадь поверхности цилиндра.
- § 2. Пирамида. Конус
- 252. Свойства пирамиды и конуса.
- 253. Объем пирамиды и конуса.
- 254. Площадь боковой поверхности правильной пирамиды и конуса.
- 255. Усеченный конус и усеченная пирамида.
- § 3. Шаровая поверхность. Шар
- 256. Шар и шаровая поверхность.
- 257. Объем шара и его частей.
- 258. Площадь поверхности шара и ее частей.
- 259. Понятие телесного угла.
- Ответы к упражнениям
- Приложения
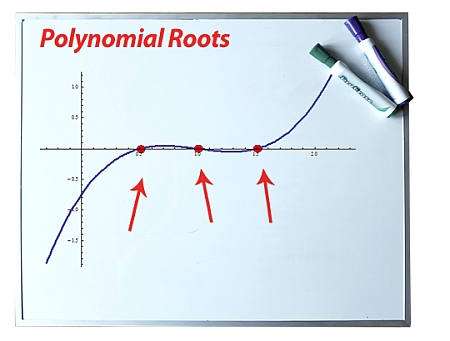
Polynomials are used to model some physical phenomena happening in real life, they are very useful in describing the situations mathematically. They are used in almost every field of Science, even outside of science like for example in Economics and other related areas. Zeros or roots of these polynomials are a very important aspect of their nature and can be very useful while describing them or plotting them on a graph. Let’s look at their definition and methods of finding out the roots in detail.
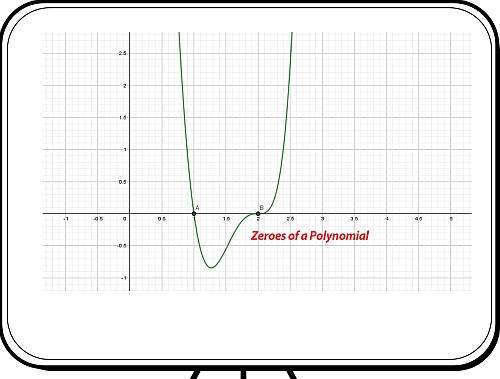
Zeros/Roots of a Polynomial
We say that x = a is the root of the polynomial if P(x) = 0 at that point. The process of finding zero is basically the process of finding out the solutions of any polynomial equation. Let’s look at some examples regarding finding zeros for a second-degree polynomial.
Question 1: Find out the zeros for P(x) = x2 + 2x – 15.
Answer:
x2 + 2x – 15 = 0
⇒ x2 + 5x – 3x – 15 = 0
⇒ x(x + 5) – 3(x + 5) = 0
⇒ (x – 3) (x + 5) = 0
⇒ x = 3, -5
Question 2: Find the out zeros for P(x) = x2 – 16x + 64.
Answer:
x2 – 16x + 64 = 0
⇒ x2 – 8x – 8x + 64 = 0
⇒ x(x – 8) – 8(x – 8) = 0
⇒ (x – 8) (x – 8) = 0
⇒ (x – 8)2 = 0
x = 8, 8
This is called a double root.
Suppose we have a polynomial P(x) = 0 which factorizes into,
P(x) = (x – r)k(x – a)m
If r is a zero of a polynomial and the exponent on its term that produced the root is k then we say that r has multiplicity k. Zeroes with a multiplicity of 1 are often called simple zeroes.
Question 3: P(x) is a degree-5 polynomial, that has been factorized for you. List the roots and their multiplicity.
P(x) = 5x5−20x4+5x3+50x2−20x−40=5(x+1)2(x−2)3
Answer:
Given, P(x) = 5(x+1)2(x−2)3
Putting this polynomial equal to zero we get the root,
x = -1, -1, 2, 2, 2
Notice that -1 occurs two times as a root. So its multiplicity is 2 while the multiplicity of the root “2” is 3.
Fundamental Theorem of Linear Algebra
If P(x) is a polynomial of degree “n” then P(x) will have exactly n zeros, some of which may repeat.
This means that if we list out all the zeroes and listing each one k times when k is its multiplicity. We will have exactly n numbers in the list. This can be useful as it can give us an idea about how many zeros should be there in a polynomial. So we can stop looking for zeros once we reach our required number of zeros.
Factor Theorem
For the polynomial P(x),
- If r is a zero of P(x) then x−r will be a factor of P(x).
- If x−r is a factor of P(x) then r will be a zero of P(x).
This can be verified by looking at previous examples. This factor theorem can lead to some interesting results,
Result 1: If P(x) is a polynomial of degree “n”, and “r” is a zero of P(x) then P(x) can be written in the following form,
P(x) = (x – r) Q(x)
Where Q(x) is a polynomial of degree “n-1” and can be found out by dividing P(x) with (x – r).
Result 2: If P(x) = (x-r)Q(x) and x = t is a zero of Q(x) then x = t will also be zero of P(x).
To verify the above fact,
Let’s say “t” is root Q(x), that means Q(t) = 0.
We know that “r” is a root of polynomial P(x), where P(x) = (x – r) Q(x),
So we need to check if x = t is also a root of P(x), let’s put x = t in P(x)
P(t) = (t – r) Q(t) = 0
So, x = t is also a root P(x).
Hence, Proved.
Sample Problems
Question 1: Given that x = 2 is a zero of P(x) = x3+2x2−5x−6. Find the other two zeroes.
Solution:
From the fundamental theorem we studied earlier, we can say that P(x) will have 3 roots because it is a three degree polynomial. One of them is x = 2.
So we can rewrite P(x),
P(x) = (x – 2) Q(x)
For finding the other two roots, we need to find out the Q(x).
Q(x) can be found out by dividing P(x) by (x-2).
After dividing, the Q(x) comes out to be,
Q(x) = x2 + 4x + 3
The remaining two roots can be found out from this,
Q(x) = x2 + 3x + x + 3
⇒ x(x + 3) + 1(x + 3)
⇒ (x + 1) (x + 3)
Q(x) = 0,
x = -1, -3
Thus, the other two roots are x = -1 and x = -3.
Question 2: Given that x = r is a root of a polynomial, find out the other roots of the polynomial.
P(x) = x3−6x2−16x; r = −2
Solution:
We know that x = -2 is a root,
So, P(x) can be rewritten as, P(x) = (x + 2) Q(x).
Now to find Q(x), we do the same thing as we did in the previous question, we divide P(x) with (x + 2).
We get,
Q(x) = x2 – 8x
Now to find the other two roots, factorize Q(x)
Q(x) = x (x – 8) = 0
So, the roots are x = 0, 8.
Thus, we have three roots, x = -2, 0, 8.
SO, this polynomial can also be written in factored form,
P(x) = (x + 2) (x) (x – 8)
Question 3: Find the roots of the polynomial, 4x3-3x2-25x-6 = 0
Solution:
Trick to solve polynomial equations with degree 3,
Find the smallest integer that can make the polynomial value 0, start with 1,-1,2, and so on…
Here we can see -2 can make the polynomial value 0.
Write (x+2) at 3 places and then write the coefficients accordingly to make the complete polynomial
4x2 (x+2) -11x(x+2) -3(x+2) =0
Now, notice carefully, the first coefficient is 4x2, because when it is multiplied with the x inside the bracket, it gives 4x3
When 4x2 is multiplied with 2, it gives 8x2, but the second term must be -3x2, hence the coefficient added next is -11x
Now, we know how to adjust the terms so that when we simplify it gives back the original polynomial.
We get a quadratic equation and a root is already there,
(4x2-11x-3)(x+2) = 0
Factorize the quadratic equation,
(4x2-12x+x-3)(x+2) = 0
(4x(x-3)+1(x-3))(x+2) = 0
(4x+1)(x-3)(x+2) = 0
x = -2, x = 3, x = -1/4
Question 4: Find the zeros of the polynomial, 4x6– 16x4= 0
Solution:
The Polynomial has up to degree 6, hence, there exist 6 roots of the polynomial.
4x4(x2-4) = 0
4x4(x2-22) = 0
4x4[(x+2)(x-2)] = 0
Therefore, x= 0, 0, 0, 0, 2, -2
Last Updated :
19 Mar, 2021
Like Article
Save Article
Инструкции:
Используйте калькулятор для нахождения нулей многочлена, показывая все этапы процесса, любого многочлена, который вы предоставите в поле формы ниже.
Нули полинома
Этот калькулятор позволит вам вычислить полиномиальные корни любого действительного многочлена, который вы предоставите. Этот многочлен может быть любым многочленом степени 1 или выше.
Например, вы можете предоставить кубический многочлен, такой как p(x) = x^3 + 2x^2 – x + 1, или вы можете предоставить многочлен с нецелыми коэффициентами, такой как p(x) = x^3 – 13/12 x^2 + 3/8 x – 1/24.
После того, как вы предоставили калькулятору действительный многочлен, для которого вы хотите вычислить его корни, вы можете нажать кнопку “Вычислить”, и вы увидите пошаговое выполнение процесса.
Необходимо отметить, что в процессе используются только элементарные методы, применяемые для нахождения корней, к которым относятся
Теорема о рациональном нуле
и
Полиномиальное деление
, а также с помощью
квадратичная формула
когда это необходимо.
Не существует общего метода, позволяющего найти ВСЕ корни для ВСЕХ возможных многочленов от
степень
больше 5, поэтому данный калькулятор будет находить только те корни, которые можно получить этими упомянутыми элементарными методами.
Что такое корень многочлена?
Учитывая
полиномиальная функция
(p(x)), мы говорим, что (x) является корнем многочлена, если:
[displaystyle p(x) = 0 ]
Говоря простым языком, корни многочлена – это точки, в которых функция многочлена (p(x)) пересекает ось x. Это хорошее представление, чтобы получить представление, но оно не совсем точное, потому что некоторые корни могут быть комплексными числами. Тогда вещественным корнем будет точка, в которой (p(x)).
Обратите внимание, что корни многочлена также называются нулями многочлена.
Каковы шаги для нахождения нулей многочлена?
-
Шаг 1:
Определите выражение, с которым вы хотите работать. Убедитесь, что оно является многочленом, и максимально упростите его -
Шаг 2:
Мы будем использоватьфакторизация полиномов
подход, чтобы найти его корень
-
Шаг 3:
Начните попытки найти элементарные (рациональные) корни сТеорема о рациональном нуле
, и использовать
Полиномиальное деление
сократить исходный многочлен, если это возможно
-
Шаг 4:
Если шаг 3 сработал, и вы смогли сократить исходный многочлен, повторите предыдущие шаги, чтобы попытаться разложить сокращенный многочлен по коэффициентам
Обычно это нелегко, и это может потребовать больших вычислительных затрат, и это не гарантированно работает, но это лучший возможный подход, если мы ограничены использованием элементарных методов.
Является ли факторизация единственным способом нахождения корней
Не совсем, но все идет рука об руку. Сайт
теорема факторов
утверждает, что (x – a) является фактором многочлена (p(x)) тогда и только тогда, когда (p(a) = 0). Другими словами, корни и факторы тесно связаны.
Теперь, для полиномов степени 2 (это,
квадратичные многочлены
) мы можем использовать явную формулу, которая хорошо известна
квадратичная формула
.
То же самое происходит для степеней 3 и 4, хотя формулы далеки от элементарных. Но для степеней 5 и выше такой формулы не существует – ключевой результат, доказанный Галуа и Абелем. Поэтому нет никакой надежды найти “общую формулу”, и именно поэтому используется более мягкая формула
полиномиальная факторизация
подход.
Общие ошибки, которых следует избегать
Часто студенты расстраиваются из-за того, что не могут найти корни заданного числа
полиномиальная функция
, скажем (p(x) = x^3+2 x^2-x+1 ), но они должны столкнуться с тем фактом, что не все многочлены можно решить с помощью элементарных инструментов.
Конечно, существует формула для решения (x^3+2 x^2-x+1 = 0 ), но она не является элементарной, и не предполагается, что студенты будут ее знать.
Советы для успеха
Всегда старайтесь составить мысленную карту того, какой будет ваша стратегия: Запишите многочлен, который у вас есть, его степень, ведущий коэффициент и постоянный коэффициент.
Постройте график полинома
если сможете, чтобы получить представление о его поведении. Есть ли очевидные факторизации, которые вы можете использовать? Используйте их. Всегда помните, что факторы = корни.
Пример: нули многочлена
Каковы нули в : (x^5 + x^4 – x^3 + x^2 – x + 1)?
Отвечать:
Для данного примера нам предоставляется следующий многочлен: (displaystyle p(x) = x^5+x^4-x^3+x^2-x+1). Для нахождения корней мы будем использовать метод факторизации.
Упрощение не требуется:
Представленное полиномиальное выражение уже упрощено, поэтому нет необходимости упрощать его дальше.
Можно отметить, что степень представленного многочлена равна (displaystyle deg(p) = 5). Также его ведущий коэффициент равен (displaystyle a_{5} = 1), а постоянный коэффициент равен (displaystyle a_0 = 1).
Теперь мы ищем целые числа, которые делят ведущий коэффициент (a_{5}) и постоянный коэффициент (a_0), который используется для поиска рациональных кандидатов.
▹ Разделителями (a_{5} = 1) являются: (pm 1).
▹ Разделителями (a_0 = 1) являются: (pm 1).
Поэтому, разделив все множители постоянного члена (a_0 = 1) на все делители (a_{5} = 1), мы получим следующий список потенциальных корней:
[pm frac{ 1}{ 1}]
Теперь необходимо оценить все потенциальные решения. Результаты, полученные при тестировании каждого кандидата, следующие:
[begin{array}{ccccclcc}
x & = & displaystyle -1 &:& & displaystyle left(-1right)^5+left(-1right)^4-left(-1right)^3+left(-1right)^2-left(-1right)+1 & = & displaystyle 4 ne 0 \\
x & = & displaystyle 1 &:& & displaystyle 1^5+1^4-1^3+1^2-1+1 & = & displaystyle 2 ne 0 \\
end{array}]
Поскольку при ручной проверке не было выявлено рациональных корней, дальнейшее упрощение с помощью основных методов невозможно, и процесс заканчивается на этом шаге.
Вывод
: В результате не было получено упрощение и не были определены корни многочлена с помощью основных методов
Пример: вычисление корней квадратичной функции
Вычислите решения: (3x^2 – 2x – 4 = 0).
Отвечать:
Необходимо решить заданное квадратное уравнение (displaystyle 3x^2-2x-4=0).
Корни квадратного уравнения вида (a x^2 + bx + c = 0) вычисляются с помощью следующего уравнения:
[x = displaystyle frac{-b pm sqrt{b^2-4ac}}{2a}]
В данном контексте уравнение, которое необходимо решить, имеет вид (displaystyle 3x^2-2x-4 = 0), что указывает на соответствующие коэффициенты:
[a = 3]
[b = -2]
[c = -4]
Сначала мы определим природу корней, вычислив дискриминант. Дискриминант вычисляется следующим образом:
[Delta = b^2 – 4ac = displaystyle left( -2right)^2 – 4 cdot left(3right)cdot left(-4right) = 52]
Так как в данном случае дискриминант (Delta = displaystyle 52 > 0) положительный, то уравнение имеет два различных вещественных корня.
Отсюда получаем:
[x = displaystyle frac{-b pm sqrt{b^2-4ac}}{2a} = displaystyle frac{2 pm sqrt{left(-2right)^2-4left(3right)left(-4right)}}{2cdot 3} = displaystyle frac{2 pm sqrt{52}}{6}]
итак, мы выяснили, что:
[ x_1 = frac{2}{6}-frac{1}{6}sqrt{52}=frac{2}{6}-frac{1}{6}cdot 2sqrt{13}=frac{2}{6}-frac{1}{3}sqrt{13}=frac{1}{3}-frac{1}{3}sqrt{13} ]
[x_2 = frac{2}{6}+frac{1}{6}sqrt{52}=frac{2}{6}+frac{1}{6}cdot 2sqrt{13}=frac{2}{6}+frac{1}{3}sqrt{13}=frac{1}{3}+frac{1}{3}sqrt{13}]
Находим, что уравнение ( displaystyle 3x^2-2x-4 = 0 ), имеет два вещественных корня, тогда:
[displaystyle 3x^2-2x-4 = 3 left(x+frac{1}{3}sqrt{13}-frac{1}{3}right)left(x-frac{1}{3}sqrt{13}-frac{1}{3}right)]
поэтому исходный многочлен факторизуется как (displaystyle p(x) = 3x^2-2x-4 = 3 left(x+frac{1}{3}sqrt{13}-frac{1}{3}right)left(x-frac{1}{3}sqrt{13}-frac{1}{3}right) ), что завершает факторизацию.
Вывод
: Таким образом, искомая факторизация имеет вид:
[displaystyle p(x) = 3x^2-2x-4 = 3 left(x+frac{1}{3}sqrt{13}-frac{1}{3}right)left(x-frac{1}{3}sqrt{13}-frac{1}{3}right)]
Найдены корни (-frac{1}{3}sqrt{13}+frac{1}{3}) и (frac{1}{3}sqrt{13}+frac{1}{3}) .
Пример: нули полинома
Вычислите нули следующего многочлена: (p(x)= x^3 – frac{13}{12} x^2 + frac{3}{8} x – frac{1}{24} ).
Отвечать:
Наконец, в данном примере мы имеем: (displaystyle p(x) = x^3-frac{13}{12}x^2+frac{3}{8}x-frac{1}{24}).
Первый Шаг:
Данное многочленное выражение является неприводимым, поэтому упрощать нечего. Мы можем перейти к его факторизации.
Обратите внимание, что степень данного многочлена равна (displaystyle deg(p) = 3), его ведущий коэффициент равен (displaystyle a_{3} = 1), а постоянный коэффициент равен (displaystyle a_0 = -frac{1}{24}).
Рациональные Корни
: Сначала мы попытаемся найти простые рациональные корни, используя теорему о рациональном нуле.
Следующая задача – найти целые числа, которые делят ведущий коэффициент (a_{3}) и постоянный коэффициент (a_0), которые будут использоваться для построения наших кандидатов в нули полиномиального уравнения.
Примечание:
В этом случае мы видим, что для того, чтобы иметь как постоянный, так и ведущий коэффициент, необходимо усилить обе стороны уравнения на (24). Эквивалентное уравнение имеет вид:
[24x^3-26x^2+9x-1 = 0]
▹ Разделителями (a_{3} = 24) являются: (pm 1,pm 2,pm 3,pm 4,pm 6,pm 8,pm 12,pm 24).
▹ Разделителями (a_0 = -1) являются: (pm 1).
Поэтому, разделив каждый делитель постоянного коэффициента (a_0 = -1) на каждый делитель ведущего коэффициента (a_{3} = 24), находим следующий список кандидатов в корни:
[pm frac{ 1}{ 1},pm frac{ 1}{ 2},pm frac{ 1}{ 3},pm frac{ 1}{ 4},pm frac{ 1}{ 6},pm frac{ 1}{ 8},pm frac{ 1}{ 12},pm frac{ 1}{ 24}]
Теперь необходимо протестировать всех кандидатов, чтобы понять, являются ли они решением. В результате тестирования каждого кандидата получено следующее:
[begin{array}{ccccclcc}
x & = & displaystyle -1 &:& & displaystyle 24cdot left(-1right)^3-26cdot left(-1right)^2+9cdot left(-1right)-1 & = & displaystyle -60 ne 0 \\
x & = & displaystyle 1 &:& & displaystyle 24cdot 1^3-26cdot 1^2+9cdot 1-1 & = & displaystyle 6 ne 0 \\
x & = & displaystyle -frac{1}{2} &:& & displaystyle 24left(frac{-1}{2}right)^3-26left(frac{-1}{2}right)^2+9left(-frac{ 1}{ 2}right)-1 & = & displaystyle -15 ne 0 \\
x & = & displaystyle frac{1}{2} &:& & displaystyle 24left(frac{1}{2}right)^3-26left(frac{1}{2}right)^2+9cdot frac{1}{2}-1 & = & displaystyle 0 \\
x & = & displaystyle -frac{1}{3} &:& & displaystyle 24left(frac{-1}{3}right)^3-26left(frac{-1}{3}right)^2+9left(-frac{ 1}{ 3}right)-1 & = & displaystyle -frac{70}{9} ne 0 \\
x & = & displaystyle frac{1}{3} &:& & displaystyle 24left(frac{1}{3}right)^3-26left(frac{1}{3}right)^2+9cdot frac{1}{3}-1 & = & displaystyle 0 \\
x & = & displaystyle -frac{1}{4} &:& & displaystyle 24left(frac{-1}{4}right)^3-26left(frac{-1}{4}right)^2+9left(-frac{ 1}{ 4}right)-1 & = & displaystyle -frac{21}{4} ne 0 \\
x & = & displaystyle frac{1}{4} &:& & displaystyle 24left(frac{1}{4}right)^3-26left(frac{1}{4}right)^2+9cdot frac{1}{4}-1 & = & displaystyle 0 \\
x & = & displaystyle -frac{1}{6} &:& & displaystyle 24left(frac{-1}{6}right)^3-26left(frac{-1}{6}right)^2+9left(-frac{ 1}{ 6}right)-1 & = & displaystyle -frac{10}{3} ne 0 \\
x & = & displaystyle frac{1}{6} &:& & displaystyle 24left(frac{1}{6}right)^3-26left(frac{1}{6}right)^2+9cdot frac{1}{6}-1 & = & displaystyle -frac{1}{9} ne 0 \\
x & = & displaystyle -frac{1}{8} &:& & displaystyle 24left(frac{-1}{8}right)^3-26left(frac{-1}{8}right)^2+9left(-frac{ 1}{ 8}right)-1 & = & displaystyle -frac{165}{64} ne 0 \\
x & = & displaystyle frac{1}{8} &:& & displaystyle 24left(frac{1}{8}right)^3-26left(frac{1}{8}right)^2+9cdot frac{1}{8}-1 & = & displaystyle -frac{15}{64} ne 0 \\
x & = & displaystyle -frac{1}{12} &:& & displaystyle 24left(frac{-1}{12}right)^3-26left(frac{-1}{12}right)^2+9left(-frac{ 1}{ 12}right)-1 & = & displaystyle -frac{35}{18} ne 0 \\
x & = & displaystyle frac{1}{12} &:& & displaystyle 24left(frac{1}{12}right)^3-26left(frac{1}{12}right)^2+9cdot frac{1}{12}-1 & = & displaystyle -frac{5}{12} ne 0 \\
x & = & displaystyle -frac{1}{24} &:& & displaystyle 24left(frac{-1}{24}right)^3-26left(frac{-1}{24}right)^2+9left(-frac{ 1}{ 24}right)-1 & = & displaystyle -frac{91}{64} ne 0 \\
x & = & displaystyle frac{1}{24} &:& & displaystyle 24left(frac{1}{24}right)^3-26left(frac{1}{24}right)^2+9cdot frac{1}{24}-1 & = & displaystyle -frac{385}{576} ne 0 \\
end{array}]
Но так как мы нашли все искомые корни среди рациональных кандидатов, то находим, что (displaystyle x^3-frac{13}{12}x^2+frac{3}{8}x-frac{1}{24} = left(x-frac{1}{2}right)left(x-frac{1}{3}right)left(x-frac{1}{4}right) ), тогда:
[displaystyle p(x) = x^3-frac{13}{12}x^2+frac{3}{8}x-frac{1}{24} = left(x-frac{1}{2}right)left(x-frac{1}{3}right)left(x-frac{1}{4}right) ]
что завершает процесс факторизации.
Результат
: Таким образом, окончательная факторизация имеет вид:
[displaystyle p(x) = x^3-frac{13}{12}x^2+frac{3}{8}x-frac{1}{24} = left(x-frac{1}{2}right)left(x-frac{1}{3}right)left(x-frac{1}{4}right)]
Таким образом, найдены корни (frac{1}{2}), (frac{1}{3}) и (frac{1}{4}).
Другие полезные калькуляторы полиномов
Нахождение нулей многочлена
является одной из вершин алгебры, в той степени, в какой фундаментальная теорема алгебры говорит о существовании n корней для многочлена степени n. Эти корни не обязательно будут все вещественными, и некоторые из них (или все) могут быть комплексными числами.
В конечном счете, почти каждая задача в алгебре и исчислении может быть сведена к нахождению корней многочлена, включая решение
полиномиальные уравнения
например, такие, которые можно найти, например, при поиске
пересечение между графами
из (y = x^2) и (y = x^3).
Метод неопределённых коэффициентов
26 июля 2022
Метод неопределённых коэффициентов — это «полуолимпиадный» приём, с помощью которого вы сможете раскладывать на множители многочлены, которые не раскладываются, и решать уравнения, которые не решаются.:)
В двух словах этот метод звучит так:
В любой непонятной ситуации вводим новую переменную. А затем думаем, что с этой переменной делать.
Сегодня мы детально изучим метод неопределённых коэффициентов. Мы разберём столько разных задач, что не понять этот приём будет просто невозможно. И да: речь пойдёт не только о многочленах.:)
Содержание
- Основная идея
- Разложение многочлена на множители
- Решение уравнений
- Деление многочлена на многочлен
- Выделение точного квадрата
- Избавление от иррациональности
- Зачем всё это нужно
1. Основная идея
Чтобы понять основную идею метода неопределённых коэффициентов, рассмотрим простую наводящую задачу. Допустим, у нас есть квадратный трёхчлен, разложенный на множители:
[Pleft( x right)=left( x-3 right)left( x+2 right)]
Если раскрыть скобки и привести подобные слагаемые, то получится тот же многочлен, записанный в стандартном виде:
[Pleft( x right)={{x}^{2}}-x-6]
Зная разложение на множители, легко получить стандартный вид многочлена. А вот обратный переход — от стандартного вида к множителям — является вычислительно сложной операцией, но всё ещё возможной: считаем дискриминант, находим корни, вспоминаем теорему Виета и т.д.
Немного усложним задачу. Рассмотрим разложение на множители многочлена четвёртой степени (почему именно четвёртой — см. урок. «Разложение на множители»):
[Pleft( x right)=left( {{x}^{2}}-3x+1 right)left( {{x}^{2}}+x+4 right)]
Раскроем скобки и приведём подобные. Вновь получим многочлен в стандартном виде:
[Pleft( x right)={{x}^{4}}-2{{x}^{3}}+2{{x}^{2}}-11x+4]
Но как выполнить обратную операцию? Как по стандартному виду многочлена определить, на какие множители его можно разложить? Тут на помощь и приходит метод неопределённых коэффициентов.
Проблема разложения на множители
Рассмотрим задачу в общем виде. Допустим, нам нужно разложить на множители многочлен четвёртой степени:
[Pleft( x right)= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]
Из курса алгебры мы знаем, что произвольный многочлен не всегда раскладывается на линейные двучлены вида $x-color{red}{a}$. Однако он совершенно точно раскладывается на квадратные трёхчлены вида $color{red}{a}{{x}^{2}}+color{red}{b}x+color{red}{c}$:
[Pleft( x right)=left(color{blue}{a}{{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+color{blue}{e}x+color{blue}{f} right)]
Записав такое разложение, мы уже наполовину выполнили задачу. Но нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ и $color{blue}{d}$, $color{blue}{e}$, $color{blue}{f}$. Отсюда, кстати, и название приёма — «метод неопределённых коэффициентов». И чтобы найти эти самые неопределённые коэффициенты, воспользуемся следующей теоремой.
Теорема о нулевом многочлене
Теорема (критерий многочлена, тождественно равного нулю). Многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]
тождественно равен нулю (т.е. при любом значении переменной $x$) тогда и только тогда, когда все его коэффициенты равны нулю:
[color{blue}{{a}_{n}}= color{blue}{{a}_{n-1}}= ldots = color{blue}{{a}_{1}}= color{blue}{{a}_{0}}= color{red}{0}]
Доказательство я вынесу на отдельную страницу (см. урок «Корни многочлена»). Потому что у этой теоремы много применений, но нас сейчас интересует не сама теорема, а лишь одно-единственное следствие из неё:
Следствие (критерий равенства двух многочленов). Пусть даны два многочлена:
[begin{align}Aleft( x right) &= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}\ Bleft( x right) &= color{blue}{{b}_{n}}{{x}^{n}}+ color{blue}{{b}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{b}_{1}}x+ color{blue}{{b}_{0}}\ end{align}]
Эти два многочлена тождественно равны друг другу (т.е. $Aleft( x right)=Bleft( x right)$ при любом $x$) тогда и только тогда, когда равны их коэффициенты при соответствующих степенях:
[color{blue}{{a}_{n}}= color{blue}{{b}_{n}}; color{blue}{{a}_{n-1}}= color{blue}{{b}_{n-1}}; ldots ; color{blue}{{a}_{1}}= color{blue}{{b}_{1}}; color{blue}{{a}_{0}}= color{blue}{{b}_{0}}]
Вот тут всё становится на свои места!
Основной алгоритм
Пусть даны два представления одного и того же многочлена. Например, в стандартном виде и разложение на множители:
[begin{align} Pleft( x right) &= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right) end{align}]
Тогда для нахождения неизвестных коэффициентов в любом из этих разложений необходимо выполнить три шага:
- Раскрыть все скобки и привести подобные, чтобы получить две записи в стандартном виде;
- Приравнять соответствующие коэффициенты, составить систему уравнений;
- Решить эту систему и правильно интерпретировать ответ.
Вот и вся суть метода. Первые два пункта очевидны. Проблемы возникают лишь на третьем шаге, поскольку зачастую системы уравнений получаются нелинейными. И мы детально разберём, как решать подобные системы.
Но для начала — парочка простых задач.:)
Задача 1.1. Основная идея
Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:
[begin{align}Pleft( x right) &=2{{x}^{4}}+3{{x}^{3}}-5x-2\ Qleft( x right) &=left( ax+3 right)left( {{x}^{3}}-b right)-3x+c\ end{align}]
Решение. Согласно Теореме 1, многочлены $Pleft( x right)$ и $Qleft( x right)$ равны, когда в точности равны их коэффициенты. Поэтому раскроем скобки в многочлене $Qleft( x right)$ и найдём эти коэффициенты:
[begin{align}Qleft( x right) &=a{{x}^{4}}+3{{x}^{3}}-abx-3b-3x+c= \ &=color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right) end{align}]
Для удобства коэффициенты выделены синим цветом. Сравним их с коэффициентами многочлена $Pleft( x right)$:
[begin{align}& color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right)= \ = & color{red}{2}{{x}^{4}}+ color{red}{3}{{x}^{3}}+left( color{red}{-5} right)x+left( color{red}{-2} right) \ end{align}]
Чтобы многочлены были равны, должны выполняться равенства
[color{blue}{a}= color{red}{2};quad color{blue}{-ab-3}= color{red}{-5};quad color{blue}{c-3b}= color{red}{-2}]
Получили систему уравнения, которая легко решается:
[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]
Ответ: $a=2$, $b=1$, $c=1$.
Задача 1.2. Альтернативный подход
Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:
[begin{align}Pleft( x right) &=3{{x}^{4}}+7{{x}^{3}}+3{{x}^{2}}+x+2\ Qleft( x right) &=left( x+1 right)left( a{{x}^{3}}+b{{x}^{2}}-x+c right)\ end{align}]
Решение. Решим эту задачу двумя способами: «чистым» методом неопределённых коэффициентов и с привлечением схемы Горнера.
Способ 1. «Чистый» метод неопределённых коэффициентов. Раскрываем скобки в многочлене $Qleft( x right)$:
[begin{align}Qleft( x right) &=a{{x}^{4}}+b{{x}^{3}}-{{x}^{2}}+cx+a{{x}^{3}}+b{{x}^{2}}-x+c= \ &= color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c} end{align}]
Приравниваем многочлены $Qleft( x right)$ и $Pleft( x right)$:
[begin{align}& color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c}= \= & color{red}{3}{{x}^{4}}+ color{red}{7}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{1}x+ color{red}{2} \ end{align}]
Получим набор из пяти уравнений:
[begin{array}{rrr}color{blue}{a}= color{red}{3}; & color{blue}{b-1}= color{red}{3}; & color{blue}{c}= color{red}{2}.\ color{blue}{a+b}= color{red}{7}; & color{blue}{c-1}= color{red}{1}; & {}\ end{array}]
Решаем систему из этих уравнений и получаем ответ:
[color{blue}{a}=color{red}{3}; color{blue}{b}=color{red}{4}; color{blue}{c}=color{red}{2}]
Способ 2. Привлечение схемы Горнера. Поскольку многочлен $Qleft( x right)$ разложен на множители, сделаем то же самое и с многочленом $Pleft( x right)$ — выделим из него множитель-двучлен $x+1$. Для этого заполним таблицу для $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r} {} & color{blue}{3} & color{blue}{7} & color{blue}{3} & color{blue}{1} & color{blue}{2}\ hline color{red}{-1} & 3 & 4 & -1 & 2 & color{green}{0}\ end{array}]
Получили остаток $r=color{green}{0}$, и многочлен $Pleft( x right)$ можно переписать так:
[Pleft( x right)=left( x+1 right)left( 3{{x}^{3}}+4{{x}^{2}}-1x+2 right)]
Приравняем многочлены $Pleft( x right)$ и $Qleft( x right)$:
[begin{align}&left( x+1 right)left( color{red}{3}{{x}^{3}}+ color{red}{4}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{2} right)= \ = &left( x+1 right)left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+left( color{blue}{-1} right)x+ color{blue}{c} right) \ end{align}]
И сразу получаем ответ:
[color{blue}{a} =color{red}{3}; color{blue}{b} =color{red}{4}; color{blue}{c} =color{red}{2}]
Ответ: $a=3$, $b=4$, $c=2$.
Если вам непонятно, как работает схема Горнера и при чём тут разложение на множители, см. урок «Схема Горнера» — это ещё один универсальный алгоритм. Который, как и метод неопределённых коэффициентов, будет полезен во многих нестандартных задачах.
2. Разложение многочлена на множители
Переходим к серьёзным задачам. Всё, что мы решали выше, сводилось к простым линейным уравнениям, которые решались обычной подстановкой.
Теперь мы разберём многочлены четвёртой степени — те самые, с которых начинали рассуждения. И заодно научимся решать нелинейные системы методом целочисленного перебора.
Задача 2.1. Самая стандартная
Задача. Разложите многочлен на множители методом неопределённых коэффициентов:
[Pleft( x right)={{x}^{4}}+2{{x}^{3}}+2{{x}^{2}}+10x+25]
Этот многочлен вообще не имеет действительных корней, в чём легко убедиться, выделив точные квадраты:
[begin{align}Pleft( x right) &=left( {{x}^{4}}+2{{x}^{3}}+{{x}^{2}} right)+left( {{x}^{2}}+10x+25 right)= \ &={{x}^{2}}{{left( x+1 right)}^{2}}+{{left( x+5 right)}^{2}} end{align}]
Полученная сумма равна нулю только если $x=-5$ и одновременно $x=0$ или $x=-1$. Что, очевидно, невозможно. Следовательно, линейных множителей в разложении не будет.
Зато квадратные множители точно будут, поэтому используем метод неопределённых коэффициентов. Предположим, что многочлен раскладывается на произведение двух квадратных трёхчленов:
[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]
Раскрываем скобки и приводим подобные:
[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ & +left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]
Сравниваем коэффициенты полученного многочлена с коэффициентами исходного:
[Pleft( x right)={{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{2}{{x}^{2}}+ color{red}{10}x+ color{red}{25}]
Выписываем равенства:
[begin{array}{rr}color{blue}{b+d}= color{red}{2}; & color{blue}{be+dc}= color{red}{10};\ color{blue}{bd+c+e}= color{red}{2}; & color{blue}{ce}= color{red}{25}.\ end{array}]
Получили систему из четырёх нелинейных уравнений. Универсального алгоритма для решения таких систем не существует. Однако здесь хорошо работает метод целочисленного перебора.
Рассмотрим последнее уравнение:
[ color{blue}{c} cdot color{blue}{e}= color{red}{25}]
Какие числа нужно перемножить, чтобы в произведении получилось 25? Вот несколько вариантов:
[begin{align}color{blue}{c} cdotcolor{blue}{e} &= color{red}{1} cdotcolor{red}{25}= color{red}{5} cdotcolor{red}{5} = \ & =left( color{red}{-1} right)cdot left( color{red}{-25} right)= \ & =left( color{red}{-5} right)cdot left( color{red}{-5} right) end{align}]
Рассмотрим вариант, когда $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$. Именно он будет правильным ответом, в чём мы сейчас убедимся.
Подставим $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$ в оставшиеся три уравнения. Получим систему
[left{ begin{align}b+d &=2 \ bd+5+5 &=2 \ 5b+5d &=10 \ end{align} right.]
Последнее уравнение является следствием первого, поэтому система равносильна двум уравнениям:
[left{ begin{align}b+d &=2 \ bd &=-8 \ end{align} right.]
Эта система имеет два решения, которые легко находятся методом подбора: $color{blue}{b} = color{red}{4}$ и $color{blue}{d}= color{red}{-2}$, либо наоборот $color{blue}{b}= color{red}{-2}$ и $color{blue}{d}= color{red}{4}$. Получаем два варианта разложения:
[begin{align}{{P}_{1}}left( x right) &=left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right)left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right) \ {{P}_{2}}left( x right) &=left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right)left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right) \ end{align}]
Но ведь на самом деле это одно и то же разложение — просто множители поменялись местами. Поэтому мы вправе выбрать любой вариант.
Запишем окончательный ответ:
[Pleft( x right)=left( {{x}^{2}}+4x+5 right)left( {{x}^{2}}-2x+5 right)]
Важное замечание. После приведения подобных и сравнения коэффициентов мы получили систему из нескольких нелинейных уравнений, которые затем начали решать методом целочисленного перебора.
Такие уравнения будут преследовать нас постоянно — это основная трудность метода неопределённых коэффициентов.
Чтобы в процессе перебора не упустить из виду какой-нибудь вариант, целесообразно составлять таблицу всех возможных вариантов. Например, для равенства $color{blue}{c}cdot color{blue}{e}= color{red}{25}$ таблица выглядит так:
[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{-1} & color{red}{5} & color{red}{-5}\ hline color{blue}{e} & color{red}{25} & color{red}{-25} & color{red}{5} & color{red}{-5}\ end{array}]
Обратите внимание: в таблице нет варианта $color{blue}{c}= color{red}{25}$, $color{blue}{e}= color{red}{1}$ и $color{blue}{c}= color{red}{-25}$, $color{blue}{e}= color{red}{-1}$, потому что они получаются из первых двух вариантов перестановкой множителей в итоговом разложении.
Тем не менее, в некоторых примерах придётся рассматривать все возможные варианты. Один из таких примеров мы рассмотрим чуть позже, а пока давайте потренируемся на более адекватных задачах.:)
Задача 2.2. Снова стандартная
Задача. Разложите многочлен на множители методом неопределённых коэффициентов:
[Pleft( x right)={{x}^{4}}+5{{x}^{3}}+5{{x}^{2}}-4x-2]
Решение. Запишем искомое разложение:
[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]
Нужно найти четыре числа: $color{blue}{b}$, $color{blue}{c}$, $color{blue}{d}$, $color{blue}{e}$. Собственно, это и есть «неопределённые коэффициенты». Раскрываем скобки и приводим подобные:
[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]
Сравниваем коэффициенты этого многочлена с коэффициентами исходного:
[Pleft( x right)={{x}^{4}}+ color{red}{5}{{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-4} right)x+left( color{red}{-2} right)]
Получаем четыре уравнения, которые должны выполняться одновременно:
[begin{array}{rr}color{blue}{b+d}= color{red}{5}; & color{blue}{be+dc}= color{red}{-4};\ color{blue}{bd+c+e}= color{red}{5}; & color{blue}{ce}= color{red}{-2}.\ end{array}]
Произведение коэффициентов $color{blue}{c}cdot color{blue}{e}= color{red}{-2}$ — отрицательное число. Положим для определённости, что $color{blue}{c} gt 0$ и $color{blue}{e} lt 0$. Выпишем все возможные варианты:
[begin{array}{r|r|r}color{blue}{c} & color{red}{1} & color{red}{2}\ hline color{blue}{e} & color{red}{-2} & color{red}{-1}\ end{array}]
Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$ и $color{blue}{e}=color{red}{-2}$. Получим систему
[left{ begin{align}b+d &=5 \ bd+1-2 &=5 \ -2b+d &=-4 end{align} right.]
Вычтем почленно из последнего уравнения первое и получим
[begin{align}-3b &=-9 \ color{blue}{b} &= color{red}{3}end{align}]
Подставляем $color{blue}{b}= color{red}{3}$ в первое уравнение и получаем $color{blue}{d}= color{red}{2}$. Найденные значения $color{blue}{b}$ и $color{blue}{d}$ удовлетворяют всем трём равенствам. Следовательно, мы нашли решение системы:
[color{blue}{b}= color{red}{3}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{2}; color{blue}{e}= color{red}{-2}]
Откуда получаем искомое разложение на множители:
[Pleft( x right)=left( {{x}^{2}}+3x+1 right)left( {{x}^{2}}+2x-2 right)]
Важное замечание. К сожалению, в процессе целочисленного перебора далеко не всегда верный вариант будет попадаться сразу, на первом же шаге. Когда я собирал материалы для этого урока, иногда верным оказывался лишь четвёртый вариант из четырёх возможных.:)
Поэтому не переживайте, когда видите несовместную систему. Это нормально и даже неизбежно.
И вообще давайте посмотрим, как это выглядит на практике. Например, рассмотрим второй вариант в только что решённой задаче: $color{blue}{c}=color{red}{2}$ и $color{blue}{e}=color{red}{-1}$. Это приведёт нас к системе уравнений:
[left{ begin{align}b+d &=5 \ bd+2-1 &=5 \ -b+2d &=-4 end{align} right.]
Складываем первое уравнение с последним — и тут же получаем проблему:
[begin{align}3d &=1 \ color{blue}{d} &= color{red}{{1}/{3};} \ end{align}]
Получили дробный коэффициент $color{blue}{d}$, откуда следует, что коэффициент $color{blue}{b}$ тоже дробный:
[color{blue}{b}=5- color{blue}{d}=color{red}{{14}/{3};}]
Но тогда не выполняется второе равенство. Следовательно, система несовместна.
Задача 2.3. Упрощённые выкладки
Задача. Разложите многочлен на множители методом неопределённых коэффициентов:
[Pleft( x right)={{x}^{4}}+{{x}^{3}}+3{{x}^{2}}+32x-10]
В этот раз распишу всё кратко — только основные выкладки. Разложим многочлен $Pleft( x right)$ на два квадратных трёхчлена:
[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]
Раскрываем скобки, приводим подобные:
[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]
Сравниваем с исходным многочленом:
[Pleft( x right)={{x}^{4}}+ color{red}{1}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{32}x+left( color{red}{-10} right)]
Получаем четыре уравнения:
[begin{array}{rr}color{blue}{b+d}= color{red}{1}; & color{blue}{be+dc}= color{red}{32};\ color{blue}{bd+c+e}= color{red}{3}; & color{blue}{ce}= color{red}{-10}.\ end{array}]
Поскольку $color{blue}{ce}= color{red}{-10} lt 0$, положим $color{blue}{c} gt 0$, $color{blue}{e} lt 0$. Возможные варианты:
[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{5} & color{red}{10} \ hline color{blue}{e} & color{red}{-10} & color{red}{-5} & color{red}{-2} & color{red}{-1} \ end{array}]
Первые три варианта дают несовместные системы с дробными коэффициентами $color{blue}{b}$ и $color{blue}{d}$ (проверьте это!). Рассмотрим последний вариант: $color{blue}{c}= color{red}{10}$, $color{blue}{e}= color{red}{-1}$. Получим систему
[left{ begin{align}b+d &=1 \ bd+10-1 &=3 \ -b+10d &=32 end{align} right.]
Решение системы: $color{blue}{b}= color{red}{-2}$, $color{blue}{d}= color{red}{3}$. Окончательное разложение на множители:
[Pleft( x right)=left( {{x}^{2}}-2x+10 right)left( {{x}^{2}}+3x-1 right)]
3. Решение уравнений методом неопределённых коэффициентов
Одно из важнейших приложений метода неопределённых коэффициентов — это решение уравнений высших степеней. В самом деле, зачем мы раскладываем многочлен $Pleft( x right)$ на множители? Обычно по одной из двух причин:
- Решить уравнение $Pleft( x right)=0$. Ведь произведение равно нулю, когда хотя бы один из множителей равен нулю;
- Сократить рациональную дробь вида ${Pleft( x right)}/{Qleft( x right)};$. В этом случае многочлен $Qleft( x right)$ также придётся разложить на множители.
Про рациональные дроби мы поговорим в отдельном уроке (см. урок «Разложение на простейшие»). А вот уравнения мы разберём сейчас.
Допустим, нужно решить уравнение вида
[color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}=0]
В левой части равенства стоит стандартный многочлен. И если коэффициенты многочлена целые, то мы уже знаем как минимум два способа решения таких уравнений:
- Теорема Безу для отыскания рациональных корней-кандидатов;
- Схема Горнера для быстрой проверки этих кандидатов.
И эта связка отлично работает, когда многочлен имеет рациональные корни вида $x={color{blue}{p}}/{color{red}{q}};$. Вот буквально: мы найдём все такие корни и решим уравнение.
А если корни иррациональны? Безу и Горнер тут бесполезны. Зато полезным оказывается разложение на множители, когда вместо большого и страшного многочлена $Pleft( x right)$ в левой части уравнения появится произведение двух многочленов меньшей степени:
[Hleft( x right)cdot Qleft( x right)=0]
А дальше всё стандартно: произведение равно нулю, когда $Hleft( x right)=0$ или $Qleft( x right)=0$. И вот мы свели исходную задачу к двум уравнениям меньших степеней, которые наверняка легко решаются.:)
Задача 3.1. «Нерешаемое» уравнение
Задача. Решите уравнение методом неопределённых коэффициентов
[{{x}^{4}}+2{{x}^{3}}+3{{x}^{2}}+2x-3=0]
Это приведённое целочисленное уравнение, но его нельзя решить по теореме Безу и схеме Горнера. Ведь целые корни этого уравнения являются делителями свободного члена $color{blue}{{a}_{0}}=-3$. Таких делителей ровно четыре:
[x=pm 1; pm 3]
И все они дают ненулевой остаток в схеме Горнера:
[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{2} & color{blue}{3} & color{blue}{2} & color{blue}{-3}\ hlinecolor{red}{1} & 1 & 3 & 6 & 8 & color{red}{5}\ hlinecolor{red}{-1} & 1 & 1 & 2 & 0 & color{red}{-3}\ hlinecolor{red}{3} & 1 & 5 & 18 & 56 & color{red}{165}\ hlinecolor{red}{-3} & 1 & -1 & 6 & -16 & color{red}{45}\ end{array}]
Остаётся только метод неопределённых коэффициентов. Разложим уравнение на произведение двух квадратных трёхчленов:
[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]
Раскроем скобки и приведём подобные в правой части равенства:
[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]
Вспоминаем коэффициенты многочлена в исходном уравнении:
[{{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{2}x+left( color{red}{-3} right)=0]
Получаем уже привычный набор из четырёх уравнений:
[begin{array}{rr} color{blue}{b+d}=color{red}{2}; & color{blue}{be+dc}=color{red}{2};\ color{blue}{bd+c+e}=color{red}{3}; & color{blue}{ce}=color{red}{-3}.\ end{array}]
Рассмотрим последнее уравнение: $color{blue}{ce}=color{red}{-3}$. Произведение отрицательно, значит, множители разных знаков. Без ограничения общности положим $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Составим таблицу вариантов:
[begin{array}{r|r|r} color{blue}{c} & color{red}{1} & color{red}{3}\ hlinecolor{blue}{e} & color{red}{-3} & color{red}{-1}\ end{array}]
Итого два варианта. Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$, $color{blue}{e}=color{red}{-3}$. Получим систему
[left{ begin{align}b+d &=2\ bd+1-3 &=3\ -3b+d &=2 end{align} right.]
Вычитая из первого уравнения последнее, получаем $color{blue}{b}=color{red}{0}$, $color{blue}{d}=color{red}{2}$, что противоречит второму уравнению. Система несовместна.
Второй вариант: $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-1}$. Система уравнений:
[left{ begin{align}b+d &=2 \ bd+3-1 &=3 \ -b+3d &=2 end{align} right.]
Складывая первое и последнее уравнение, получаем $color{blue}{b}=color{red}{1}$, $color{blue}{d}=color{red}{1}$. При подстановке во второе уравнение получаем верное числовое равенство. Следовательно, мы нашли решение:
[color{blue}{b}=color{red}{1}; color{blue}{c}=color{red}{3}; color{blue}{d}=color{red}{1}; color{blue}{e}=color{red}{-1}]
Переписываем уравнение:
[left( {{x}^{2}}+x+3 right)left( {{x}^{2}}+x-1 right)=0]
Многочлен в первой скобке не имеет действительных корней, во второй — имеет:
[{{x}^{2}}+x-1=0]
Дискриминант положителен:
[D={{1}^{2}}-4cdot 1cdot left( -1 right)=1+4=5]
Корней будет два:
[x=frac{-1pm sqrt{5}}{2}]
Неудивительно, что эти корни не были обнаружены по теореме Безу. Ведь они являются иррациональными.:)
Ответ: $x=frac{-1pm sqrt{5}}{2}$.
Задача 3.2. «Нерешаемое» уравнение — 2
Задача. Решите уравнение методом неопределённых коэффициентов:
[{{x}^{4}}-4{{x}^{3}}+5{{x}^{2}}-2x-6=0]
Это задание похоже на предыдущее, поэтому распишем всё кратко. Ожидаемое разложение на множители:
[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]
Найдём такое разложение методом неопределённых коэффициентов. Раскрываем скобки, приводим подобные:
[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]
Сравниваем с коэффициентами исходного многочлена:
[{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-2} right)x+left( color{red}{-6} right)=0]
Выписываем четыре уравнения:
[begin{array}{rr} color{blue}{b+d}=color{red}{-4}; & color{blue}{be+dc}=color{red}{-2};\ color{blue}{bd+c+e}=color{red}{5}; & color{blue}{ce}=color{red}{-6}.\ end{array}]
Поскольку $color{blue}{ce}=color{red}{-6}$, полагаем $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Возможные варианты
[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{3} & color{red}{6}\ hlinecolor{blue}{e} & color{red}{-6} & color{red}{-3} & color{red}{-2} & color{red}{-1}\ end{array}]
Перебирая варианты, обнаруживаем, что правильная комбинация — это $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-2}$:
[left{ begin{align} b+d &=-4 \ bd+3-2 &=5 \ -2b+3d &=-2 end{align} right.]
Дважды прибавим к последнему уравнению первое — получим
[begin{align} 5d&=-10 \ color{blue}{d} &= color{red}{-2} \ color{blue}{b} &= color{red}{-2} end{align}]
Следовательно, исходное уравнение примет вид
[left( {{x}^{2}}-2x+3 right)left( {{x}^{2}}-2x-2 right)=0]
Многочлен в первой скобке корней не имеет (в этом легко убедиться, посчитав дискриминант). Рассмотрим вторую скобку:
[{{x}^{2}}-2x-2=0]
Дискриминант положительный:
[D={{left( -2 right)}^{2}}-4cdot1cdot left( -2 right)=4+8=12]
Уравнение имеет два корня:
[x=frac{2pm sqrt{12}}{2}=frac{2pm 2sqrt{3}}{2}=1pm sqrt{3}]
Ответ: $x=1pm sqrt{3}$.
Задача 3.3. Более сложное уравнение
Задача. Решите уравнение методом неопределённых коэффициентов:
[2{{x}^{4}}-4{{x}^{3}}+{{x}^{2}}-6x-3=0]
Это уравнение принципиально отличается от предыдущих тем, что старший коэффициент $color{blue}{{a}_{4}}=2$. Многочлен не является приведённым, поэтому разложение на множители, вообще говоря, выглядит так:
[left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]
Итого шесть неизвестных коэффициентов. Для сравнения: раньше их было всего четыре.
Однако задачу можно существенно упростить, если сделать два допущения:
- Оба старших коэффициента — $color{blue}{a}$ и $color{blue}{d}$ — являются целыми и положительными.
- Положим для определённости, что $color{blue}{a} gt color{blue}{d}$.
В этом и состоит ключевая идея метода неопределённых коэффициентов: мы вводим дополнительные ограничения, которые в итоге почти наверняка выполняются. Да, есть небольшой риск «промахнуться» в своих допущениях, но это компенсируется многократным упрощением дальнейших выкладок.
В нашем случае из двух допущений немедленно следует, что $color{blue}{a}=color{red}{2}$, $color{blue}{b}=color{red}{1}$, и уравнение примет вид
[left( color{red}{2}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]
Осталось всего четыре неизвестных коэффициента. Раскроем скобки и приведём подобные:
[begin{align}color{red}{2}{{x}^{4}}+left( color{blue}{b+2e} right){{x}^{3}} &+left( color{blue}{be+c+2f} right){{x}^{2}}+ \ &+left( color{blue}{bf+ce} right)x+ color{blue}{cf}=0 \ end{align}]
Сравним с коэффициентами исходного уравнения:
[color{red}{2}{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+color{red}{1}{{x}^{2}}+left( color{red}{-6} right)x+left( color{red}{-3} right)=0]
Получим четыре уравнения, но из-за коэффициента $color{blue}{a}=color{red}{2}$ они отличаются от привычных:
[begin{array}{rr} color{blue}{b+2e}= color{red}{-4}; & color{blue}{bf+ce}= color{red}{-6};\ color{blue}{be+c+2f}= color{red}{1}; & color{blue}{cf}= color{red}{-3}.\ end{array}]
Многочлены в первой и второй скобке не являются взаимозаменяемыми (поскольку у них разные коэффициенты при ${{x}^{2}}$), поэтому необходимо рассмотреть все возможные комбинации, дающие $color{blue}{cf}= color{red}{-3}$:
[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{3} & color{red}{-1} & color{red}{-3}\ hlinecolor{blue}{f} & color{red}{-3} & color{red}{-1} & color{red}{3} & color{red}{1}\ end{array}]
Рассмотрим каждую комбинацию. В первом случае быстро обнаружится, что система несовместна. А вот второй случай, когда $color{blue}{c}= color{red}{3}$ и $color{blue}{f}= color{red}{-1}$, представляет интерес:
[left{ begin{align}b+2e &=-4 \ be+3-2 &=1 \ -b+3e &=-6 end{align} right.]
Складываем первое уравнение с последним — получаем
[begin{align}5e &=-10 \ color{blue}{e} &= color{red}{-2} \ color{blue}{b} &= color{red}{0} end{align}]
Итак, система совместна. Получили разложение на множители:
[left( 2{{x}^{2}}+3 right)left( {{x}^{2}}-2x-1 right)=0]
Многочлен в первых скобках принимает только положительные значения, поэтому не имеет корней:
[2{{x}^{2}}+3ge 0+3 gt 0]
Рассмотрим вторые скобки:
[{{x}^{2}}-2x-1=0]
Это квадратное уравнение. Дискриминант положительный:
[D={{2}^{2}}-4cdot 1cdot left( -1 right)=4+4=8]
Следовательно, уравнение имеет два различных корня:
[x=frac{2pm sqrt{8}}{2}=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]
Это и есть корни исходного уравнения четвёртой степени.
Ответ: $x=1pm sqrt{2}$.
4. Деление многочлена на многочлен
Ещё одна задача, где работает метод неопределённых коэффициентов — это деление одного многочлена на другой с остатком. Напомню, что разделить многочлен $Pleft( x right)$ на двучлен $Tleft( x right)$ с остатком — это значит представить его в виде
[Pleft( x right)=Qleft( x right)cdot Tleft( x right)+Rleft( x right)]
При этом степень остатка $Rleft( x right)$ должна быть меньше степени делителя $Tleft( x right)$. Кроме того,
[deg Qleft( x right)+deg Tleft( x right)=deg Pleft( x right)]
При соблюдении таких ограничений многочлены $Qleft( x right)$ и $Rleft( x right)$ всегда определяются однозначно. Их коэффициенты мы как раз и будем находить.
Задача 4.1. Деление на двучлен
Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена
[Pleft( x right)={{x}^{3}}-5{{x}^{2}}+15x-6]
на двучлен $Tleft( x right)=x-3$.
Итак, мы хотим представить многочлен $Pleft( x right)$ в виде
[Pleft( x right)=Qleft( x right)cdot left( x-3 right)+Rleft( x right)]
где $Qleft( x right)$ — неполное частное. Точнее, $Qleft( x right)$ — квадратный трёхчлен, потому что
[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)= \ &=3-1=2end{align}]
Кроме того, степень делителя $deg Tleft( x right)=1$, поэтому степень остатка $deg Rleft( x right)=0$, т.е. $Rleft( x right)$ — это просто число. С учётом этих фактов многочлен $Pleft( x right)$ примет вид
[Pleft( x right)=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x-3 right)+ color{blue}{d}]
Раскроем скобки, приведём подобные слагаемые:
[Pleft( x right)= color{blue}{a}{{x}^{3}}+left( color{blue}{b-3a} right){{x}^{2}}+left( color{blue}{c-3b} right)x+left( color{blue}{d-3c} right)]
С другой стороны, изначально тот же многочлен $Pleft( x right)$ имел вид
[Pleft( x right)= color{red}{1}{{x}^{3}}+left( color{red}{-5} right){{x}^{2}}+ color{red}{15}x+left( color{red}{-6} right)]
Приравниваем коэффициенты и получаем четыре равенства:
[begin{array}{rr} color{blue}{a}= color{red}{1}; & color{blue}{c-3b}= color{red}{15};\ color{blue}{b-3a}= color{red}{-5}; & color{blue}{d-3c}= color{red}{-6}.\ end{array}]
Это система из четырёх уравнений с четырьмя неизвестными, которая легко решается:
[color{blue}{a}= color{red}{1}; color{blue}{b}= color{red}{-2}; color{blue}{c}= color{red}{9}; color{blue}{d}= color{red}{21}]
Подставим найденные числа в $Qleft( x right)$ и $Rleft( x right)$:
[begin{align} & Qleft( x right)={{x}^{2}}-2x+9 \ & Rleft( x right)=21 \end{align}]
Ответ: $Qleft( x right)={{x}^{2}}-2x+9$, $Rleft( x right)=21$.
Поскольку мы делим $Pleft( x right)$ на двучлен $x-color{red}{3}$, составим таблицу для $x=color{red}{3}$:
[begin{array}{r|r|r|r|r} {} & color{blue}{1} & color{blue}{-5} & color{blue}{15} & color{blue}{-6}\ hlinecolor{red}{3} & 1 & -2 & 9 & color{green}{21}\ end{array}]
Перепишем многочлен $Pleft( x right)$ согласно этой таблице и сравним с записью для метода неопределённых коэффициентов:
[begin{align}Pleft( x right) &=left( color{red}{1}{{x}^{2}}- color{red}{2}x+ color{red}{9} right)left( x-color{red}{3} right)+ color{green}{21}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x- color{red}{3} right)+ color{blue}{d} end{align}]
Получили те же числа, что и при решении «напролом».
Впрочем, такие рассуждения актуальны лишь при делении на двучлен вида $x-color{red}{a}$. В следующем задании они нам уже не помогут.:)
Задача 4.2. Многочлен с параметром
Задача. При каких значениях параметров $a$ и $b$ многочлен
[Pleft( x right)={{x}^{3}}+a{{x}^{2}}-x+b]
делится без остатка на многочлен
[Tleft( x right)={{x}^{2}}+2x+5]
Решение. Если многочлен $Pleft( x right)$ делится без остатка на многочлен $Tleft( x right)$, то его можно представить в виде
[Pleft( x right)=Qleft( x right)cdot Tleft( x right)]
Здесь многочлен $Qleft( x right)$ — это частное, и его степень равна
[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=3-2=1]
Итак, $Qleft( x right)$ — линейный двучлен вида $color{blue}{c}x+color{blue}{d}$ (коэффициенты $color{blue}{a}$ и $color{blue}{b}$ уже заняты в условии задачи). Выражение для $Pleft( x right)$ можно переписать так:
[Pleft( x right)=left( color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x+5 right)]
Найдём коэффициенты $color{blue}{c}$ и $color{blue}{d}$. Раскрываем скобки (стандартная процедура для метода неопределённых коэффициентов) и приводим подобные:
[Pleft( x right)= color{blue}{c}{{x}^{3}}+left( color{blue}{2c+d} right){{x}^{2}}+left( color{blue}{5c+2d} right)x+ color{blue}{5d}]
Сравниваем с коэффициентами исходного многочлена:
[Pleft( x right)= color{red}{1}{{x}^{3}}+ color{red}{a}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{b}]
Приравниваем соответствующие «красные» и «синие» коэффициенты и получаем четыре равенства:
[begin{array}{rr}color{blue}{c}= color{red}{1}; & color{blue}{5c+2}d= color{red}{-1};\color{blue}{2c+d}= color{red}{a}; & color{blue}{5d}= color{red}{b}.\end{array}]
Итак, у нас четыре линейных уравнения и четыре переменных. Эта система имеет только одно решение:
[ color{blue}{a}= color{red}{-1}; color{blue}{b}= color{red}{-15}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{-3}]
Впрочем, нас интересуют лишь переменные $color{blue}{a}$ и $color{blue}{b}$.
Ответ: $a=-1$, $b=-15$.
Задача 4.3. Квадратный трёхчлен
Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена
[Pleft( x right)=2{{x}^{2}}+3x-3]
на двучлен $Tleft( x right)=2x-1$.
Решение. Частное $Qleft( x right)$ имеет степень
[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=2-1=1]
Следовательно, $Qleft( x right)$ — линейный двучлен вида $color{blue}{a}x+ color{blue}{b}$, а остаток $Rleft( x right)$ — просто число $color{blue}{c}$. С учётом этого перепишем многочлен $Pleft( x right)$:
[begin{align}Pleft( x right) &=left( ax+b right)left( 2x-1 right)+c= \ &=2a{{x}^{2}}-ax+2bx-b+c= \ &= color{blue}{2a}{{x}^{2}}+left( color{blue}{2b-a} right)x+left( color{blue}{c-b} right) end{align}]
Сравним с исходным видом этого же многочлена:
[Pleft( x right)= color{red}{2}{{x}^{2}}+color{red}{3}x+left( color{red}{-3} right)]
Приравниваем соответствующие коэффициенты — получаем три уравнения:
[color{blue}{2a}=color{red}{2};quadcolor{blue}{2b-a}=color{red}{3};quadcolor{blue}{c-b}=color{red}{-3}]
Эта система легко решается:
[color{blue}{a}=color{red}{1}; color{blue}{b}=color{red}{2}; color{blue}{c}=color{red}{-1}]
Следовательно, неполное частное $Qleft( x right)=x+2$ и остаток $Rleft( x right)=-1$.
Ответ: $Qleft( x right)=x+2$, $Rleft( x right)=-1$.
Задача 4.4. Сложный многочлен
Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена
[Pleft( x right)={{x}^{5}}-1]
на квадратный трёхчлен $Tleft( x right)={{x}^{2}}+2x-1$.
Решение. На самом деле это несложная задача, но вычислений будет много. Запишем результат деления с остатком:
[Pleft( x right)=Qleft( x right)cdot left( {{x}^{2}}+2x-1 right)+Rleft( x right)]
Сразу найдём степени неполного частного и остатка:
[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)=5-2=3 \ deg Rleft( x right) & lt deg Tleft( x right)=2Rightarrow deg Rleft( x right)=1 \ end{align}]
Переходим к методу неопределённых коэффициентов. Сначала запишем общий вид многочленов $Qleft( x right)$ и $Rleft( x right)$:
[begin{align}Qleft( x right) &= color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} \ Rleft( x right) &= color{blue}{k}x+ color{blue}{l} \ end{align}]
Пусть вас не пугает большое количество переменных. Это нормально для многочленов высших степеней. Подставим наши выражения в формулу для $Pleft( x right)$:
[begin{align}Pleft( x right) &=left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x-1 right)+ \ &+ color{blue}{k}x+ color{blue}{l} \ end{align}]
Раскрываем скобки. Для удобства запишем одночлены одинаковой степени в одном и том же столбце:
[begin{array}{rrrrrr} color{blue}{a}{{x}^{5}} & + color{blue}{2a}{{x}^{4}} & – color{blue}{a}{{x}^{3}} & {} & {} & {}\ {} & + color{blue}{b}{{x}^{4}} & + color{blue}{2b}{{x}^{3}} & – color{blue}{b}{{x}^{2}} & {} & {}\ {} & {} & + color{blue}{c}{{x}^{3}} & + color{blue}{2c}{{x}^{2}} & – color{blue}{c}x & {}\ {} & {} & {} & + color{blue}{d}{{x}^{2}} & + color{blue}{2d}x & – color{blue}{d}\ {} & {} & {} & {} & + color{blue}{k}x & + color{blue}{l}\ end{array}]
Приводим подобные слагаемые:
[begin{align}Pleft( x right) &=color{blue}{a}{{x}^{5}}+left( color{blue}{2a+b} right){{x}^{4}}+left( color{blue}{-a+2b+c} right){{x}^{3}}+ \ &+left( color{blue}{-b+2c+d} right){{x}^{2}}+left( color{blue}{-c+2d+k} right)x+left( color{blue}{-d+l} right) \ end{align}]
Сравниваем эту запись с исходным многочленом:
[Pleft( x right)= color{red}{1}cdot {{x}^{5}}+ color{red}{0}cdot {{x}^{4}}+ color{red}{0}cdot {{x}^{3}}+ color{red}{0}cdot {{x}^{2}}+ color{red}{0}cdot x+left( color{red}{-1} right)]
Получаем шесть уравнений, которые последовательно решаются:
[begin{array}{ll}color{blue}{a}= color{red}{1} & color{blue}{d}=b-2c= color{red}{-12}\ color{blue}{b}=-2a= color{red}{-2} & color{blue}{k}=c-2d= color{red}{29}\ color{blue}{c}=a-2b= color{red}{5} & color{blue}{l}=d-1= color{red}{-13}\ end{array}]
Подставим найденные коэффициенты в выражения для $Qleft( x right)$ и $Rleft( x right)$:
[begin{align}Qleft( x right) &={{x}^{3}}-2{{x}^{2}}+5x-12 \ Rleft( x right) &=29x-13 \ end{align}]
Мы нашли неполное частное и остаток от деления. Это и есть окончательный ответ.
Ответ: $Qleft( x right)={{x}^{3}}-2{{x}^{2}}+5x-12$, $Rleft( x right)=29x-13$.
5. Выделение точного квадрата
Ещё одно приложение метода неопределённых коэффициентов — это «сворачивание» многочленов по формулам сокращённого умножения:
[begin{align}{{left( apm b right)}^{2}} &={{a}^{2}}pm 2ab+{{b}^{2}} \ {{left( apm b right)}^{3}} &={{a}^{3}}pm 3{{a}^{2}}b+3a{{b}^{2}}pm {{b}^{3}} \ end{align}]
Здесь всё как в разложении на множители: раскрывать скобки и привести подобные легко, а вот обратный переход — по коэффициентам «угадать» формулу сокращённого умножения — операция весьма нетривиальная.
Такие «нетривиальные операции» регулярно встречаются в задачах с параметрами и при работе с корнями. Параметрам посвящён отдельный урок, а вот корни мы рассмотрим прямо сейчас.
Задача 5.1. Избавление от корня
Задача. Упростите выражение
[sqrt{7+4sqrt{3}}]
Решение. Единственное, что здесь можно упростить — это избавиться от внешнего большого корня. Для этого нужно представить подкоренное выражение в виде точного квадрата:
[7+4sqrt{3}={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}}]
Почему именно такая конструкция возводится в квадрат? Всё просто: в исходной сумме мы видим одно слагаемое с корнем и одно слагаемое без него. Для получения такой суммы исходные слагаемые тоже должны быть разными: одно с корнем, а другое — без него.
В этом случае числа $color{blue}{a}$ и $color{blue}{b}$ будут либо рациональными, либо вообще целыми. И в этом вся суть метода неопределённых коэффициентов, потому что найти такие числа не составит особого труда — достаточно раскрыть скобки по формуле квадрата суммы:
[begin{align}{{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}} &={color{blue}{a}^{2}}+2color{blue}{ab}sqrt{3}+{{left( color{blue}{b}sqrt{3} right)}^{2}}= \ &=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3} end{align}]
Сравниваем полученное разложение с исходным выражением:
[color{red}{7}+color{red}{4}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3}]
Чтобы эти выражения были гарантированно равны друг другу, достаточно потребовать, чтобы слагаемые без корня совпадали. Как и слагаемые с корнем:
[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=7 \ 2color{blue}{ab} &=4 end{align} right.]
Это нелинейная система с двумя переменными, которая легко решается методом подбора:
[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{2}^{2}}+3cdot {color{red}{1}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{2}cdotcolor{red}{1} end{align} right.]
Научиться раскладывать целые числа на «правильные» слагаемые и множители — вопрос небольшой практики. Просто попробуйте — и вы поймёте, насколько это быстро и легко.
Нам остаётся лишь записать решение:
[color{blue}{a}=color{red}{2}; color{blue}{b}=color{red}{1}]
Затем подставить найденные числа в исходное выражение:
[begin{align}sqrt{7+4sqrt{3}} &=sqrt{{{left( 2+sqrt{3} right)}^{2}}}= \ &=left| 2+sqrt{3} right|= \ &=2+sqrt{3} end{align}]
Ответ: $2+sqrt{3}$.
Важное замечание. Помните, что корень не просто «сжигает» квадрат вокруг выражения — на их месте появляется модуль:
[sqrt{{{a}^{2}}}=left| a right|]
Потому что арифметический квадратный корень — это по определению всегда неотрицательное число:
[begin{align}sqrt{{{5}^{2}}} &=left| 5 right|=5 \ sqrt{{{left( -8 right)}^{2}}} &=left| -8 right|=8 end{align}]
Когда под модулем стоит иррациональное выражение, его знак следует проверять отдельно. Иначе даже при правильном ответе его можно счесть недостаточно обоснованным.
Если вы забыли, как проверять знаки таких выражений, вернитесь к уроку «Знаки иррациональных выражений». В двух словах: для такой проверки используются либо цепочки неравенств, либо цепочки равносильных преобразований.
В следующем задании мы отработаем оба способа.
Задача 5.2. Предварительные преобразования
Задача. Упростите выражение
[sqrt{37-5sqrt{48}}]
Под корнем мы видим ещё один корень: $sqrt{48}$ — это большое число, с ним сложно работать. Поэтому прежде чем искать точный квадрат, немного упростим выражение:
[begin{align}sqrt{37-5sqrt{48}} &=sqrt{37-5sqrt{color{red}{16}cdot 3}}= \ &=sqrt{37-5cdot color{red}{4}cdot sqrt{3}}= \ &=sqrt{37-20sqrt{3}} end{align}]
Теперь представляем подкоренное выражение в виде точного квадрата
[37-20sqrt{3}={{left( color{blue}{a}- color{blue}{b}sqrt{3} right)}^{2}}]
Обратите внимание: перед нами квадрат разности. Потому что в исходном подкоренном выражении элементы не складывались, а именно вычитались. Этот факт ещё даст о себе знать, когда будем выяснять знак подмодульного выражения.
Ну а пока всё просто. Сравниваем старую запись и новую:
[color{red}{37}-color{red}{20}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)-2color{blue}{ab}sqrt{3}]
Получаем систему уравнений:
[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=37 \ 2color{blue}{ab} &=20 end{align} right.]
Второе уравнение перепишем в виде $color{blue}{ab}=10$, а затем разложим правые части равенств на «правильные» слагаемые и множители:
[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{5}^{2}}+3cdot {color{red}{2}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{5}cdotcolor{red}{2} end{align} right.]
Получили красивое решение:
[color{blue}{a}=color{red}{5}; color{blue}{b}=color{red}{2}]
Возвращаемся к исходному выражению и извлекаем корень:
[sqrt{37-20sqrt{3}}=sqrt{{{left( 5-2sqrt{3} right)}^{2}}}=left| 5-2sqrt{3} right|]
Чтобы раскрыть модуль, нужно выяснить знак иррационального числа $5-2sqrt{3}$. Для этого можно заметить, что $sqrt{3} lt 2$, поэтому
[5-2sqrt{3} gt 5-2cdot 2=1 gt 0]
Это и есть цепочка неравенств. Также можно напрямую сравнить число $5-2sqrt{3}$ с нулём:
[begin{align}5-2sqrt{3} &vee 0 \ 5 &vee 2sqrt{3} \ 25 &vee 12 end{align}]
Очевидно, что $25 gt 12$, поэтому мы ещё раз убеждаемся, что исходное число положительное, и модуль раскрывается со знаком «плюс»:
[left| 5-2sqrt{3} right|=5-2sqrt{3}]
Ответ: $5-2sqrt{3}$.
Но всё это были довольно простые примеры с квадратным корнем. Как насчёт корней $n$-й степени?
Задача 5.3. Проблема с корнем
Задача. Упростите выражение
[sqrt[3]{sqrt{10}-3}cdot sqrt[6]{19+6sqrt{10}}]
Решение. Для начала вспомним свойства корней $n$-й кратности. Их можно умножать:
[sqrt[n]{a}cdot sqrt[n]{b}=sqrt[n]{acdot b}]
А также извлекать корень из корня:
[sqrt[k]{sqrt[m]{a}}=sqrt[mcdot k]{a}]
В частности, второй корень из задачи можно переписать так:
[sqrt[6]{19+6sqrt{10}}=sqrt[3]{sqrt{19+6sqrt{10}}}]
Чтобы избавиться от внутреннего квадратного корня, представим подкоренное выражение в виде точного квадрата. Но поскольку $sqrt{10}=sqrt{5}cdot sqrt{2}$, возможны два варианта:
[begin{align}19+6sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}} \ 19+6sqrt{10} &={{left( color{blue}{a}sqrt{2}+ color{blue}{b}sqrt{5} right)}^{2}} \ end{align}]
Однако в исходном выражении (т.е. прямо в условии задачи) есть ещё один $sqrt{10}$, который пока никак не преобразуется и никуда не денется, поэтому целесообразно рассмотреть лишь первый вариант:
[begin{align} color{red}{19}+ color{red}{6}sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}}= \ &=ldots =left( {color{blue}{a}^{2}}+10{color{blue}{b}^{2}} right)+ 2color{blue}{ab}sqrt{10} end{align}]
Получаем стандартную систему:
[left{ begin{align}{color{blue}{a}^{2}}+10{color{blue}{b}^{2}} &=19 \ 2 color{blue}{ab} &=6 end{align} right.]
Второе уравнение равносильно $color{blue}{ab}=3$, и всю систему можно переписать так:
[left{ begin{align}{color{blue}{a}^{2}}+10cdot {color{blue}{b}^{2}} &={color{red}{3}^{2}}+10cdot {color{red}{1}^{2}} \ color{blue}{a} cdotcolor{blue}{b} &= color{red}{3}cdotcolor{red}{1} end{align} right.]
Очевидно, что $color{blue}{a}=color{red}{3}$, $color{blue}{b}=color{red}{1}$, поэтому
[begin{align}sqrt{19+6sqrt{10}} &=sqrt{{{left( 3+sqrt{10} right)}^{2}}}= \ &=left| 3+sqrt{10} right|= \ &=3+sqrt{10} end{align}]
Возвращаемся к исходному заданию:
[sqrt[3]{sqrt{10}-3}cdot sqrt[3]{3+sqrt{10}}=sqrt[3]{{{left( sqrt{10} right)}^{2}}-{{3}^{2}}}=1]
Ответ: 1.
Наконец, рассмотрим задание, где требуется выделить куб суммы и куб разности. Как вы понимаете, это задание совершенно другого уровня сложности.:)
Задача 5.4. Куб суммы и куб разности
Задача. Упростите выражение
[sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}]
Чтобы «красиво» извлечь корень третьей степени, нужно представить подкоренное выражение в виде точного куба. Начнём с суммы:
[begin{align}color{red}{10}+ color{red}{6}sqrt{3} &={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{3}}= \ &={color{blue}{a}^{3}}+3{color{blue}{a}^{2}} color{blue}{b}sqrt{3}+3color{blue}{a}{color{blue}{b}^{2}}cdot 3+{color{blue}{b}^{3}}cdot 3sqrt{3}= \ &=left( {color{blue}{a}^{3}}+9color{blue}{a}{color{blue}{b}^{2}} right)+left( 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} right)sqrt{3} end{align}]
Получаем систему с двумя неизвестными:
[left{ begin{align}{color{blue}{a}^{2}}+9color{blue}{a}{color{blue}{b}^{2}} &=10 \ 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} &=6 end{align} right.]
Методом подбора находим решение: $color{blue}{a}=color{red}{1}$, $color{blue}{b}=color{red}{1}$. Несмотря на грозный внешний вид, такие системы часто легко решаются простым перебором с проверкой:
[{{left( 1+1cdot sqrt{3} right)}^{3}}=1+3sqrt{3}+9+3sqrt{3}=10+6sqrt{3}]
Возвращаемся к исходному выражению:
[begin{align}& sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}= \ = &sqrt[3]{left( 1+sqrt{3} right)}+sqrt[3]{left( 1-sqrt{3} right)}= \ = & 1+sqrt{3}+1-sqrt{3}=2 \ end{align}]
Ответ: 2.
6. Избавление от иррациональности в знаменателе
Последний приём, который мы рассмотрим в этом уроке — избавление от иррациональностей в знаменателе с помощью неопределённых коэффициентов.
Из курса алгебры мы помним, как избавлять от простых иррациональностей. Например, домножение на квадратный корень:
[frac{1}{sqrt{2}}=frac{1cdotcolor{red}{sqrt{2}}}{sqrt{2}cdotcolor{red}{sqrt{2}}}=frac{sqrt{2}}{2}]
Или домножение на сопряжённое:
[frac{1}{sqrt{3}-1}=frac{1cdot left( color{red}{sqrt{3}+1} right)}{left( sqrt{3}-1 right)cdot left( color{red}{sqrt{3}+1} right)}=frac{sqrt{3}+1}{2}]
Но всё это касается лишь самых простых корней — квадратных. Уже в случае с кубическими корнями такой фокус не пройдёт. Тут-то на помощь к нам и приходят коэффициенты-переменные.
Задача 6.1. Корень третьей степени
Задача. Избавьтесь от иррациональности в знаменателе:
[frac{10}{1+sqrt[3]{9}}]
Поскольку это иррациональное число, то никакие преобразования не избавят нас от корней полностью.
Заметим, что $sqrt[3]{9}=sqrt[3]{3}cdot sqrt[3]{3}$. Попробуем возвести число $sqrt[3]{3}$ в разные степени:
[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{3} right)}^{n}} & sqrt[3]{3} & sqrt[3]{9} & 3 & 3sqrt[3]{3} & 3sqrt[3]{9} & 9\ end{array}]
Итак, все степени числа $sqrt[3]{3}$ можно разделить на три типа:
- Целые числа $color{blue}{a}in mathbb{Z}$;
- Иррациональные выражения вида $color{blue}{b}sqrt[3]{3}$ где $color{blue}{b}in mathbb{Z}$;
- Выражения вида $color{blue}{c}sqrt[3]{9}$, где $color{blue}{c}in mathbb{Z}$.
Логично предположить (и это можно доказать), что результат деления на $1+sqrt[3]{9}$ можно представить в виде комбинации слагаемых этих трёх типов:
[frac{10}{1+sqrt[3]{9}}=color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]
Однако нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$ и $color{blue}{c}$. Найти их — в этом и состоит суть задачи.:)
И тут к делу подключается метод неопределённых коэффициентов. Преобразуем уравнение так, чтобы найти эти коэффициенты. Для начала умножим обе части на $1+sqrt[3]{9}$:
[10=left( 1+sqrt[3]{9} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)]
Раскрываем скобки:
[color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}+ color{blue}{a}sqrt[3]{9}+ 3color{blue}{b}+ 3color{blue}{c}sqrt[3]{3}=10]
Группируем слагаемые относительно одинаковых корней:
[begin{align}& left( color{blue}{a}+ 3color{blue}{b} right)+left( color{blue}{b}+ 3color{blue}{c} right)sqrt[3]{3}+left( color{blue}{a} + color{blue}{c} right)sqrt[3]{9}= \ = &color{red}{10}+ color{red}{0}cdot sqrt[3]{3}+ color{red}{0}cdot sqrt[3]{9} \ end{align}]
Выше мы предположили, что все коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ — целые (в крайнем случае рациональные). Следовательно, множители при корнях $sqrt[3]{3}$ и $sqrt[3]{9}$ должны быть равны нулю (иначе число слева будет иррациональным):
[begin{align}color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align}]
С учётом этих двух условий само уравнение примет вид
[color{blue}{a}+ 3color{blue}{b}= color{red}{10}]
Получили систему из трёх уравнений с тремя неизвестными:
[left{ begin{align}color{blue}{a}+ 3color{blue}{b} &= color{red}{10} \ color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align} right.]
Все уравнения линейные, система решается элементарно. Решением будут числа $color{blue}{a}= color{red}{1}$, $color{blue}{b}= color{red}{3}$, $color{blue}{c}= color{red}{-1}$, поэтому исходное выражение можно переписать так:
[frac{10}{1+sqrt[3]{9}}= color{red}{1}+ color{red}{3}cdot sqrt[3]{3}- color{red}{1}cdot sqrt[3]{9}]
Ответ: $1+3sqrt[3]{3}-sqrt[3]{9}$.
Важное замечание. Чтобы избавиться от иррациональности конкретно в этой задаче, достаточно было домножить числитель и знаменатель дроби на недостающую часть куба суммы:
[begin{align} frac{10}{1+sqrt[3]{9}} &=frac{10cdot left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}{left( 1+sqrt[3]{9} right)left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}= \ &=ldots =1+3sqrt[3]{3}-sqrt[3]{9} end{align}]
Однако такой подход не работает, когда в знаменателе стоит конструкция вида $color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}$. А метод неопределённых коэффициентов работает всегда.:)
Попробуем решить ещё одну задачу такого же типа.
Задача 6.2. То же самое, но чуть сложнее
Задача. Избавьтесь от иррациональности в знаменателе:
[frac{46}{2-3sqrt[3]{2}}]
Решение. Найдём несколько степеней числа $sqrt[3]{2}$:
[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{2} right)}^{n}} & sqrt[3]{2} & sqrt[3]{4} & 2 & 2sqrt[3]{2} & 2sqrt[3]{4} & 4\ end{array}]
На будущее: для корня $n$-й степени достаточно рассмотреть первые $n$ степеней. В нашем случае достаточно было выписать $sqrt[3]{2}$, $sqrt[3]{4}$ и $sqrt[3]{8}=2$ — новых иррациональных чисел мы уже не получим.
Итак, решаем задачу методом неопределённых коэффициентов. Попробуем подобрать целые (или рациональные) числа $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ такие, что
[frac{46}{2-3sqrt[3]{2}}= color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4}]
Умножаем обе части уравнения на $2-3sqrt[3]{2}$:
[left( 2-3sqrt[3]{2} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4} right)=46]
Раскрываем скобки, приводим подобные:
[begin{align}2color{blue}{a}+ 2color{blue}{b}sqrt[3]{2}+ 2color{blue}{c}sqrt[3]{4} -3color{blue}{a}sqrt[3]{2} -3color{blue}{b}sqrt[3]{4} -6color{blue}{c} &= color{red}{46} \ left( 2color{blue}{a}- 6color{blue}{c} right)+left( 2color{blue}{b}- 3color{blue}{a} right)sqrt[3]{2}+left( 2color{blue}{c}- 3color{blue}{b} right)sqrt[3]{4} &= color{red}{46}end{align}]
Это равенство верно при соблюдении трёх условий:
[left{ begin{align}2color{blue}{a}- 6color{blue}{c} &= color{red}{46} \ 2color{blue}{b}- 3color{blue}{a} &=color{red}{0} \ 2color{blue}{c}- 3color{blue}{b} &=color{red}{0} \ end{align} right.]
Это система из трёх линейных уравнений с тремя неизвестными. Её решение:
[color{blue}{a}= color{red}{-4}; color{blue}{b}= color{red}{-6}; color{blue}{c}= color{red}{-9}]
Следовательно, исходное выражение можно переписать так:
[frac{46}{2-3sqrt[3]{2}}= color{red}{-4-6}cdot sqrt[3]{2} color{red}{-9}cdot sqrt[3]{4}]
Ответ: $-4-6sqrt[3]{2}-9sqrt[3]{4}$.
Важное замечание. Здесь тоже можно «составить» куб суммы в знаменателе:
[begin{align}frac{46}{2-3sqrt[3]{2}} &=frac{46cdot left( color{red}{{{2}^{2}}+2cdot 3sqrt[3]{2}+9sqrt[3]{4}} right)}{{{2}^{3}}-{{left( 3sqrt[3]{2} right)}^{3}}} \ &= ldots =-4-6sqrt[3]{2}-9sqrt[3]{4} end{align}]
Почему не использовать этот приём всегда? Потому что в следующей задаче он уже не сработает. Там помогут только неопределённые коэффициенты и решение системы уравнений.
Задача 6.3. Когда кубы уже не помогают
Это задание чуть сложнее, потому что здесь не помогут формулы сокращённого умножения. Да и сами вычисления будут чуть сложнее, чем в предыдущих задачах.
Задача. Избавьтесь от иррациональности в знаменателе:
[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}]
Мы уже встречались с числами $sqrt[3]{3}$ и $sqrt[3]{9}$, поэтому знаем, что исходное выражение можно представить в виде
[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}= color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]
Преобразуем выражение, избавившись от дроби:
[left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)cdot left( 1+sqrt[3]{3}-sqrt[3]{9} right)= color{red}{2}]
Раскроем скобки, приведём подобные:
[begin{align}left( color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} right) &+left( color{blue}{a}+ color{blue}{b} -3color{blue}{c} right)sqrt[3]{3}+ \ &+left( -color{blue}{a}+ color{blue}{b}+ color{blue}{c} right)sqrt[3]{9}= color{red}{2} \ end{align}]
Это равенство возможно при соблюдении трёх условий:
[left{ begin{align}color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} &= color{red}{2} \ color{blue}{a}+ color{blue}{b}- 3color{blue}{c} &= color{red}{0} \ -color{blue}{a}+ color{blue}{b}+ color{blue}{c} &= color{red}{0} end{align} right.]
Три линейных уравнения, три переменных. Всё решается легко:
[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]
Следовательно, исходное выражение перепишется так:
[frac{2}{1+ sqrt[3]{3}- sqrt[3]{9}}= color{red}{2}+ color{red}{1}cdot sqrt[3]{3}+ color{red}{1}cdot sqrt[3]{9}]
Ответ: $2+sqrt[3]{3}+sqrt[3]{9}$.
Как видите, никакие кубы суммы здесь уже не помогут.:)
7. Зачем всё это нужно
В этом уроке мы рассмотрели пять типов задач, которые можно решить методом неопределённых коэффициентов. У внимательного читателя наверняка возник вопрос: зачем вообще нужен этот метод, когда многие из этих задач можно решить проще и быстрее с помощью отдельных специальных приёмов?
В самом деле:
- Большинство многочленов отлично раскладываются на множители с помощью теоремы Безу и схемы Горнера — об этом мы говорили в отдельном уроке. Но только при условии, что среди корней есть рациональные.
- То же самое можно сказать и про решение уравнений.
- Делить многочлены друг на друга с остатком вообще лучше столбиком. Это самый быстрый и самый надёжный способ — при условии, что среди коэффициентов нет параметров.
- Точные квадраты зачастую можно подобрать, если немного подумать. Как и дополнительные множители для избавления от иррациональности. Если только это не «тяжёлый» случай, где формулы сокращённого умножения не работают.
Так зачем же нужен метод неопределённых коэффициентов? Всё дело в тех самых оговорках: «при условии», «только если не тяжёлый случай» и т.д.
Основная сила этого метода — в его универсальности. Да, считать придётся чуть больше, чем при использовании более специализированных приёмов. И да: целочисленный перебор не всегда приводит нас к успеху.
Но перед нами прежде всего универсальный алгоритм. Который точно работает — всегда, везде, без всяких оговорок. И если задача не решается методом неопределённых коэффициентов, то «специализированные» приёмы тем более не помогут.
Более того: область применения этого метода намного шире. Например, мы не рассмотрели разложение рациональных дробей в простейшие, а это очень важный приём, например, в интегрировании — и ему тоже нет альтернативы.
Поэтому берите на вооружение всё, что вы сегодня узнали, практикуйтесь — и да прибудут с вами решённые задачи, олимпиады и университетские зачёты и экзамены.:)
Смотрите также:
- Бином Ньютона

- Схема Горнера

- Сравнение дробей

- Четырехугольная пирамида в задаче C2

- Задача B5: площадь кольца

- Сечения и двугранные углы

Содержание:
Многочлен – это сумма одночленов, причем сам одночлен – это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена 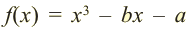
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной 
По определению одночлена числа и буквы (в нашем случае одна буква — 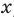 ) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида
) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида 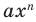 , где
, где 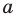 — некоторое число. Поэтому одночлен от одной переменной
— некоторое число. Поэтому одночлен от одной переменной 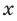 — это выражение вида
— это выражение вида 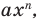 где
где 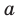 — некоторое число,
— некоторое число, 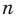 — целое неотрицательное число. Если
— целое неотрицательное число. Если 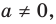 то показатель степени
то показатель степени 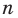 переменной
переменной 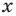 называется степенью одночлена. Например,
называется степенью одночлена. Например, 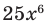 — одночлен шестой степени,
— одночлен шестой степени, 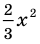 — одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку
— одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку 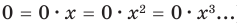 ).
).
По определению многочлен от одной переменной  — это сумма одночленов от одной переменной
— это сумма одночленов от одной переменной  . Поэтому
. Поэтому
многочленом от одной переменной  : называется выражение вида
: называется выражение вида
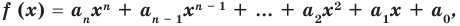 (1)
(1)
где коэффициенты 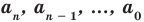 — некоторые числа.
— некоторые числа.
Если 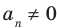 , то этот многочлен называют многочленом
, то этот многочлен называют многочленом 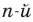 степени от переменной
степени от переменной 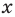 . При этом член
. При этом член 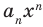 называют старшим членом многочлена
называют старшим членом многочлена 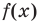 , число
, число 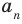 — коэффициентом при старшем члене, а член
— коэффициентом при старшем члене, а член 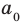 — свободным членом. Например,
— свободным членом. Например, 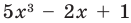 — многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
— многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена  записывают так:
записывают так:
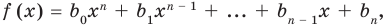
где 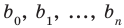 — некоторые числа.
— некоторые числа.
Теорема 1. Одночлены 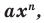 где
где 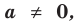 и
и 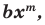 где
где 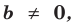 , тождественно равны тогда и только тогда, когда
, тождественно равны тогда и только тогда, когда 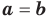 и
и 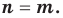 Одночлен
Одночлен 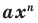 тождественно равен нулю тогда и только тогда, когда
тождественно равен нулю тогда и только тогда, когда 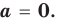
Поскольку равенство одночленов
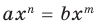 (2)
(2)
выполняется при всех значениях 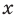 (по условию эти одночлены тождественно равны), то, подставляя в это равенство
(по условию эти одночлены тождественно равны), то, подставляя в это равенство 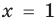 , получаем, что
, получаем, что 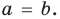 Сокращая обе части равенства (2) на
Сокращая обе части равенства (2) на 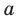 (где
(где 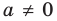 по условию), получаем
по условию), получаем 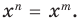 При
При 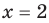 из этого равенства имеем:
из этого равенства имеем: 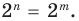 Поскольку 2
Поскольку 2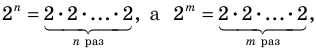 то равенство
то равенство 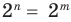 возможно только тогда, когда
возможно только тогда, когда 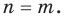 Таким образом, из тождественного равенства
Таким образом, из тождественного равенства 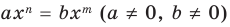 получаем, что
получаем, что 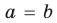 и
и 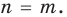 Если известно, что
Если известно, что 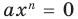 для всех
для всех 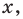 то при
то при 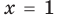 получаем
получаем 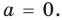 Поэтому одночлен
Поэтому одночлен 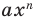 тождественно равен нулю при
тождественно равен нулю при 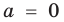 (тогда
(тогда 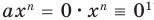 ).
).
Далее любой одночлен вида 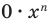 будем заменять на 0.
будем заменять на 0.
Теорема 2. Если многочлен 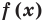 тождественно равен нулю (то есть принимает нулевые значения при всех значениях
тождественно равен нулю (то есть принимает нулевые значения при всех значениях 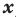 ), то все его коэффициенты равны нулю.
), то все его коэффициенты равны нулю.
 Значком
Значком  обозначено тождественное равенство многочленов.
обозначено тождественное равенство многочленов.
Для доказательства используем метод математической индукции. Пусть 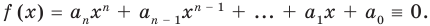
При  имеем
имеем 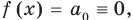 поэтому
поэтому 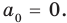 То есть в этом случае утверждение теоремы выполняется.
То есть в этом случае утверждение теоремы выполняется.
Предположим, что при 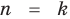 это утверждение также выполняется: если многочлен
это утверждение также выполняется: если многочлен 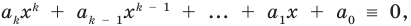 то
то 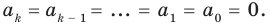
Докажем, что данное утверждение выполняется и при 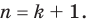 Пусть
Пусть 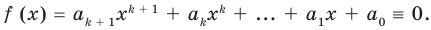 (3)
(3)
Поскольку равенство (3) выполняется при всех значениях  , то, подставляя в это равенство
, то, подставляя в это равенство 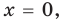 получаем, что
получаем, что 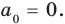 Тогда равенство (3) обращается в следующее равенство:
Тогда равенство (3) обращается в следующее равенство: 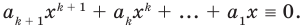 Вынесем
Вынесем  в левой части этого равенства за скобки и получим
в левой части этого равенства за скобки и получим
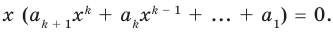 (4)
(4)
Равенство (4) должно выполняться при всех значениях  . Для того чтобы оно выполнялось при
. Для того чтобы оно выполнялось при  должно выполняться тождество
должно выполняться тождество
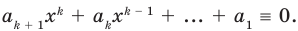 В левой части этого тождества стоит многочлен со степенями переменной от
В левой части этого тождества стоит многочлен со степенями переменной от  до
до 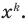 Тогда по предположению индукции все его коэффициенты равны нулю:
Тогда по предположению индукции все его коэффициенты равны нулю: 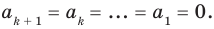 Но мы также доказали, что
Но мы также доказали, что 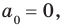 поэтому наше утверждение выполняется и при
поэтому наше утверждение выполняется и при 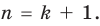 Таким образом, утверждение теоремы справедливо для любого целого неотрицательного
Таким образом, утверждение теоремы справедливо для любого целого неотрицательного 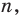 то есть для всех многочленов.
то есть для всех многочленов.
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 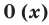 или просто
или просто  (поскольку
(поскольку 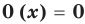 ).
).
Теорема 3. Если два многочлена 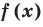 и
и 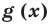 тождественно равны, то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
тождественно равны, то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
Пусть многочлен 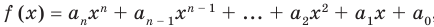 , а многочлен
, а многочлен 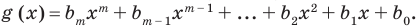 Рассмотрим многочлен
Рассмотрим многочлен 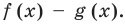 Поскольку многочлены
Поскольку многочлены 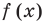 и
и 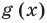 по условию тождественно равны, то многочлен
по условию тождественно равны, то многочлен 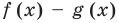 тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
Но 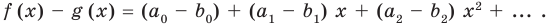 Тогда
Тогда 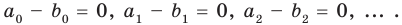 Отсюда
Отсюда 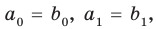
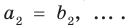 Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например,
Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например, 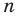 больше
больше 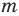 ), то коэффициенты разности будут равны нулю. Поэтому начиная с (
), то коэффициенты разности будут равны нулю. Поэтому начиная с (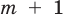 -го номера все коэффициенты
-го номера все коэффициенты 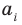 также будут равны нулю. То есть действительно многочлены
также будут равны нулю. То есть действительно многочлены 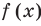 и
и 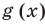
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение 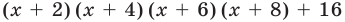
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 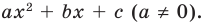 Получаем тождество:
Получаем тождество:
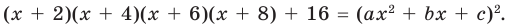 (5)
(5)
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях  получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
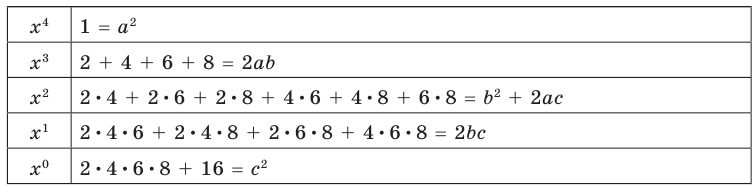
Из первого равенства получаем 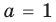 или
или 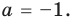
При 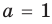 из второго равенства имеем а из третьего —
из второго равенства имеем а из третьего —  Как видим, при этих значениях
Как видим, при этих значениях  и
и 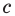 последние два равенства также выполняются. Следовательно, тождество (5) выполняется при
последние два равенства также выполняются. Следовательно, тождество (5) выполняется при 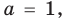
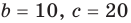 (аналогично можно также получить
(аналогично можно также получить 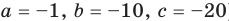 ). Таким образом,
). Таким образом, 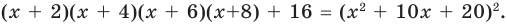
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 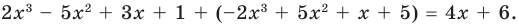 При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей степени слагаемого.
При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей степени слагаемого.
Например, 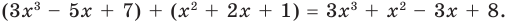 Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что целое число
Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что целое число  делится на целое число
делится на целое число 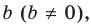 если существует такое целое число
если существует такое целое число 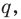 что
что 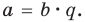
Определение: Многочлен  делится на многочлен
делится на многочлен 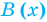 (где
(где 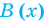 — не нулевой многочлен), если существует такой многочлен
— не нулевой многочлен), если существует такой многочлен  что
что 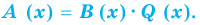
Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен  делится на многочлен
делится на многочлен  (где
(где  — не нулевой многочлен) с остатком, если существует такая пара многочленов
— не нулевой многочлен) с остатком, если существует такая пара многочленов  и
и  что
что  причем степень остатка
причем степень остатка  меньше степени делителя
меньше степени делителя  (в этом случае многочлен
(в этом случае многочлен  называют неполным частным.)
называют неполным частным.)
Например, поскольку 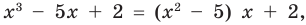 то при делении многочлена
то при делении многочлена 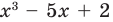 на многочлен
на многочлен 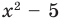 получаем неполное частное
получаем неполное частное 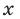 : и остаток 2.
: и остаток 2.
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 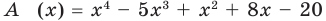 на многочлен
на многочлен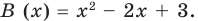
Решение:
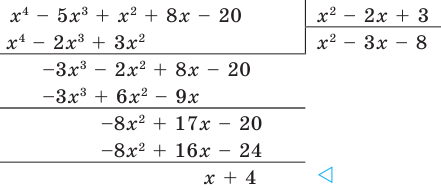 Докажем, что полученный результат действительно является результатом деления
Докажем, что полученный результат действительно является результатом деления 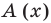 на
на 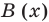 с остатком.
с остатком.
Если обозначить результат выполнения первого шага алгоритма через 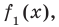 второго шага — через
второго шага — через 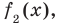 третьего — через
третьего — через  то операцию деления, выполненную выше, можно записать в виде системы равенств:
то операцию деления, выполненную выше, можно записать в виде системы равенств:
 (1)
(1)
 (2)
(2)
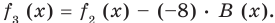 (3)
(3)
Сложим почленно равенства (1), (2), (3) и получим
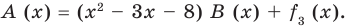 (4)
(4)
Учитывая, что степень многочлена 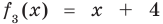 меньше степени делителя
меньше степени делителя 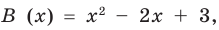 обозначим
обозначим 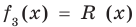 (остаток), а
(остаток), а 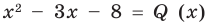 (неполное частное). Тогда из равенства (4) имеем:
(неполное частное). Тогда из равенства (4) имеем: 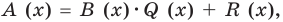 то есть
то есть 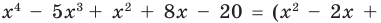
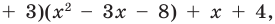 а это и означает, что мы разделили
а это и означает, что мы разделили 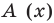 на
на 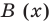 с остатком.
с остатком.
Очевидно, что приведенное обоснование можно провести для любой пары многочленов  и
и 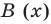 в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого
в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого 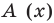 и делителя
и делителя 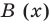 (где
(где 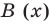 — не нулевой многочлен) найти неполное частное
— не нулевой многочлен) найти неполное частное 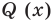 и остаток
и остаток 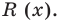
Отметим, что в случае, когда степень делимого 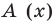 меньше степени делителя
меньше степени делителя 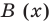 , считают, что неполное частное
, считают, что неполное частное 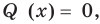 а остаток
а остаток 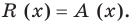
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 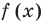 на двучлен
на двучлен 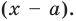 Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен
Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен 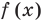 на двучлен
на двучлен 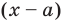 , то получим
, то получим
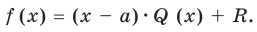
Это равенство выполняется тождественно, то есть при любом значении  При
При 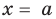 имеем
имеем 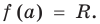 Полученный результат называют теоремой Безу
Полученный результат называют теоремой Безу .
.
Теорема 1 (теорема Безу). Остаток от деления многочлена 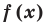 на двучлен
на двучлен 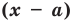 равен
равен 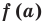 (то есть значению многочлена при
(то есть значению многочлена при 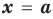 ).
).
Пример №2
Докажите, что 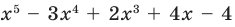 делится на
делится на 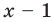 без остатка.
без остатка.
Решение:
► Подставив в 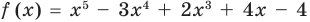 вместо
вместо  значение 1, получаем:
значение 1, получаем:  . Таким образом, остаток от деления
. Таким образом, остаток от деления 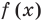 на
на  равен 0, то есть
равен 0, то есть 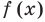 делится на
делится на  без остатка. <]
без остатка. <]
Определение: Число 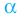 называют корнем многочлена
называют корнем многочлена 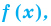 если
если
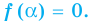
Если многочлен  делится на
делится на  то
то  — корень этого многочлена.
— корень этого многочлена.
 Безу Этьен (1730-1783) — французский математик, внесший значительный вклад в развитие теории алгебраических уравнений.
Безу Этьен (1730-1783) — французский математик, внесший значительный вклад в развитие теории алгебраических уравнений.
Действительно, если 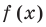 делится на
делится на 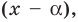 то
то  и поэтому
и поэтому 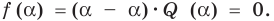 Таким образом,
Таким образом, 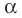 — корень многочлена
— корень многочлена 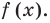
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 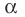 является корнем многочлена
является корнем многочлена 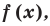 то этот многочлен делится на двучлен
то этот многочлен делится на двучлен 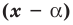 без остатка.
без остатка.
По теореме Безу остаток от деления 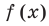 на
на  равен
равен 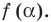 Но по условию
Но по условию 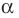 — корень
— корень 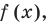 таким образом,
таким образом, 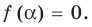
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен  имеет попарно разные корни
имеет попарно разные корни 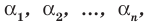 то он делится без остатка на произведение
то он делится без остатка на произведение 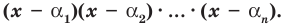
Для доказательства используем метод математической индукции.
При 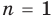 утверждение доказано в теореме 2.
утверждение доказано в теореме 2.
Допустим, что утверждение справедливо при 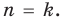 То есть если
То есть если 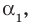
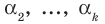 попарно разные корни многочлена
попарно разные корни многочлена 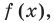 то он делится на произведение
то он делится на произведение 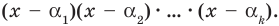 Тогда
Тогда
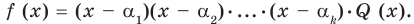 (1)
(1)
Докажем, что утверждение теоремы справедливо и при 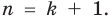 Пусть
Пусть 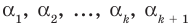 — попарно разные корни многочлена
— попарно разные корни многочлена 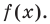 Поскольку
Поскольку 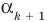 — корень
— корень 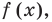 то
то 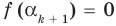 . Принимая во внимание равенство (1), которое выполняется согласно допущению индукции, получаем:
. Принимая во внимание равенство (1), которое выполняется согласно допущению индукции, получаем:
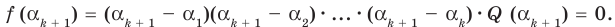
По условию все корни 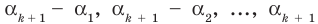 разные, поэтому ни одно из чисел
разные, поэтому ни одно из чисел 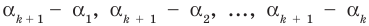 не равно нулю. Тогда
не равно нулю. Тогда 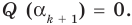 Таким образом,
Таким образом, 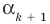 — корень многочлена
— корень многочлена 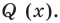 Тогда по теореме 2 многочлен
Тогда по теореме 2 многочлен 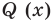 делится на
делится на 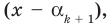 то есть
то есть 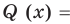
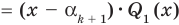 и из равенства (1) имеем
и из равенства (1) имеем

Это означает, что  делится на произведение
делится на произведение
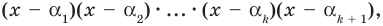 то есть теорема доказана и при
то есть теорема доказана и при 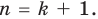
Таким образом, теорема справедлива для любого натурального 
Следствие. Многочлен степени  имеет не больше
имеет не больше 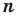 разных корней.
разных корней.
Допустим, что многочлен 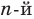 степени имеет
степени имеет 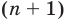 разных корней:
разных корней: 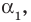
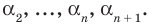 Тогда
Тогда 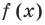 делится на произведение
делится на произведение 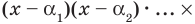
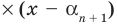 многочлен степени
многочлен степени 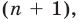 но это невозможно. Поэтому многочлен
но это невозможно. Поэтому многочлен 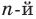 степени не может иметь больше чем
степени не может иметь больше чем 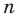 корней.
корней.
Пусть теперь многочлен 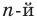 степени
степени 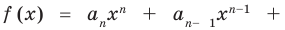
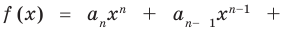 имеет
имеет  разных корней
разных корней 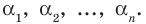 Тогда этот многочлен делится без остатка на произведение
Тогда этот многочлен делится без остатка на произведение 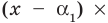
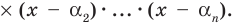 Это произведение является многочленом той же
Это произведение является многочленом той же
 степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
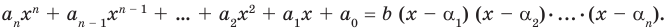 (2)
(2)
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 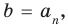 то есть
то есть
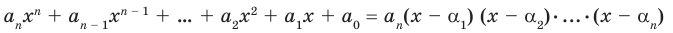 (3)
(3)
Сравнивая коэффициенты при одинаковых степенях  в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
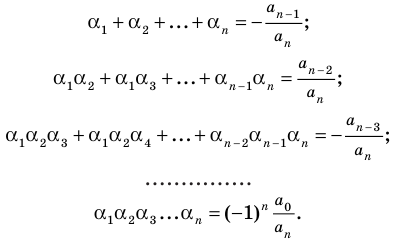 (4)
(4)
Например, при 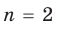 имеем:
имеем:
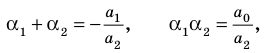
а при 
 (5)
(5)
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 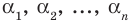 были корнями многочлена
были корнями многочлена
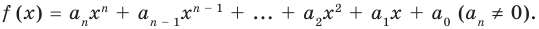
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 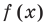 разные. Введем понятие кратного корня многочлена.
разные. Введем понятие кратного корня многочлена.
Если многочлен 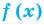 делится без остатка на
делится без остатка на 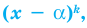 но не делится без остатка на
но не делится без остатка на 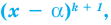 то говорят, что число
то говорят, что число  является корнем кратности
является корнем кратности  многочлена
многочлена 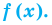
Например, если произведение  записать в виде многочлена, то для этого многочлена число
записать в виде многочлена, то для этого многочлена число 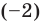 является корнем кратности 3, число 1 — корнем кратности 2, а число
является корнем кратности 3, число 1 — корнем кратности 2, а число 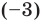 — корнем кратности 1.
— корнем кратности 1.
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена 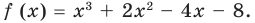
Решение:
► 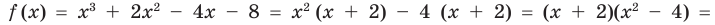
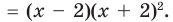
Поэтому 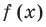 имеет корни:
имеет корни:  (поскольку
(поскольку  — корень кратности 2).
— корень кратности 2).
Проверим справедливость формулы (5). В нашем случае:  Тогда
Тогда
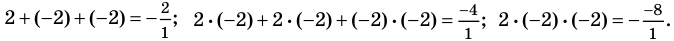
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения 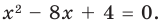
Решение:
► Обозначим корни уравнения 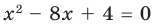 через
через  и
и 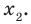 Тогда корнями искомого уравнения должны быть числа
Тогда корнями искомого уравнения должны быть числа 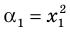 и
и 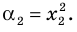 Поэтому искомое уравнение имеет вид
Поэтому искомое уравнение имеет вид 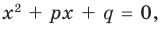 где
где
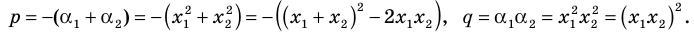
По формулам Виета имеем 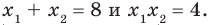 Отсюда находим, что
Отсюда находим, что 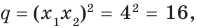 а
а 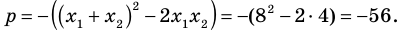 Таким образом, искомое уравнение имеет вид
Таким образом, искомое уравнение имеет вид 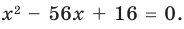
Схема Горнера
Делить многочлен 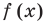 на двучлен
на двучлен 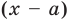 иногда удобно с помощью
иногда удобно с помощью
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 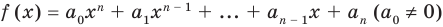 необходимо разделить на двучлен
необходимо разделить на двучлен 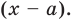 В результате деления многочлена
В результате деления многочлена 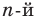 степени на многочлен первой степени получим некоторый многочлен
степени на многочлен первой степени получим некоторый многочлен 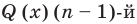 степени (то есть
степени (то есть 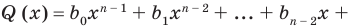
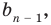 , где
, где 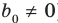 ) и остаток
) и остаток 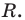 Тогда
Тогда 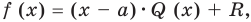 то есть
то есть
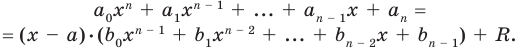
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях 
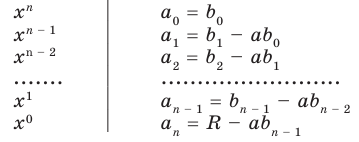
Найдем из этих равенств коэффициенты 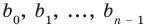 и остаток
и остаток 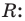

Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент  неполного частного, достаточно предыдущий найденный коэффициент
неполного частного, достаточно предыдущий найденный коэффициент  умножить на
умножить на  и добавить
и добавить 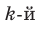 коэффициент делимого. Эту процедуру целесообразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.
коэффициент делимого. Эту процедуру целесообразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.

Пример №5
Разделите по схеме Горнера многочлен 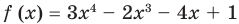 на двучлен
на двучлен 
Решение:
► Запишем сначала все коэффициенты многочлена 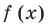 (если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:
(если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:

Таким образом, 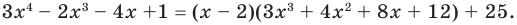
Пример №6
Проверьте, является ли 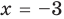 корнем многочлена
корнем многочлена 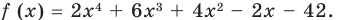
Решение:
► По теореме Безу остаток от деления многочлена  на
на 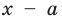 равен
равен 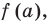 поэтому найдем с помощью схемы Горнера остаток от деления
поэтому найдем с помощью схемы Горнера остаток от деления 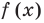 на
на 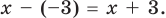

Поскольку 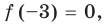 то
то 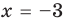 — корень многочлена
— корень многочлена 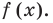
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 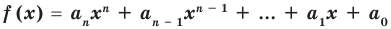 имеет рациональный корень
имеет рациональный корень 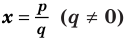 , то
, то 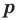 является делителем свободного члена
является делителем свободного члена  a
a 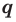 — делителем коэффициента при старшем члене
— делителем коэффициента при старшем члене 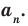
Если 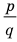 является корнем многочлена
является корнем многочлена 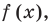 то
то 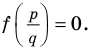 Подставляем
Подставляем
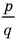 вместо
вместо 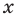 в
в 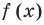 и из последнего равенства имеем
и из последнего равенства имеем
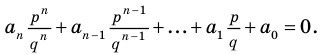 (1)
(1)
Умножим обе части равенства (1) на 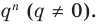 Получаем
Получаем
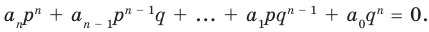 (2)
(2)
В равенстве (2) все слагаемые, кроме последнего, делятся на 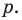 Поэтому
Поэтому 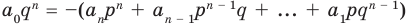 делится на
делится на 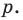
Но когда мы записываем рациональное число в виде 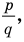 то эта дробь считается несократимой, то есть
то эта дробь считается несократимой, то есть  и
и  не имеют общих делителей. Произведение
не имеют общих делителей. Произведение 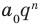 может делиться на
может делиться на 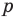 (если
(если 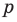 и
и 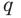 — взаимно простые числа) только тогда, когда
— взаимно простые числа) только тогда, когда 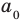 делится на
делится на 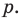 Таким образом,
Таким образом, 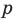 — делитель свободного члена
— делитель свободного члена 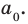
Аналогично все слагаемые равенства (2), кроме первого, делятся на 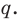 Тогда
Тогда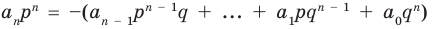 делится на
делится на  Поскольку
Поскольку  и
и 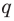 взаимно простые числа, то
взаимно простые числа, то 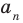 делится на
делится на 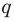 , следовательно,
, следовательно, 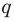 — делитель коэффициента при старшем члене.
— делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять 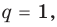 то корнем многочлена будет целое число
то корнем многочлена будет целое число 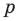 — делитель
— делитель 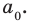 Таким образом, имеет место:
Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 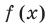 коэффициент
коэффициент 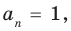 то делителями
то делителями 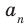 могут быть только числа
могут быть только числа 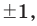 то есть
то есть 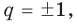 и имеет место:
и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена 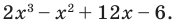
Решение:
► Пусть несократимая дробь 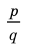 является корнем многочлена. Тогда
является корнем многочлена. Тогда  необходимо искать среди делителей свободного члена, то есть среди чисел
необходимо искать среди делителей свободного члена, то есть среди чисел 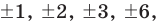 a
a 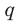 — среди делителей старшего коэффициента:
— среди делителей старшего коэффициента: 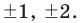
Таким образом, рациональные корни многочлена необходимо искать среди чисел 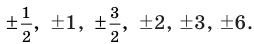 Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера.
Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера.
При 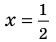 имеем следующую таблицу.
имеем следующую таблицу.
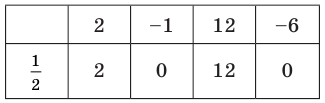
Кроме того, по схеме Горнера можно записать, что
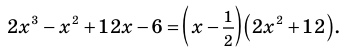
Многочлен 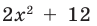 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень
не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень 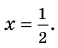
Пример №8
Разложите многочлен 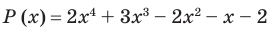 на множители.
на множители.
Решение:
► Ищем целые корни многочлена среди делителей свободного члена: 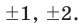
Подходит 1. Делим  на
на  с помощью схемы Горнера.
с помощью схемы Горнера.
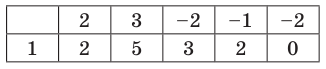
Тогда 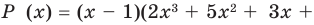
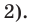
Ищем целые корни кубического многочлена 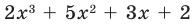 среди делителей его свободного члена:
среди делителей его свободного члена:  Подходит
Подходит 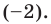 Делим на
Делим на 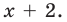

Имеем 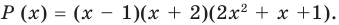
Квадратный трехчлен 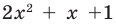 не имеет действительных корней и на линейные множители не раскладывается.
не имеет действительных корней и на линейные множители не раскладывается.
Ответ: 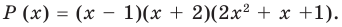
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 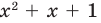 не имеет действительных корней). Таким образом, многочлен
не имеет действительных корней). Таким образом, многочлен  степени не всегда можно разложить на произведение линейных множителей. Но многочлен нечетной степени всегда можно разложить на произведение линейных и квадратных множителей, а многочлен четной степени — на произведение квадратных трехчленов.
степени не всегда можно разложить на произведение линейных множителей. Но многочлен нечетной степени всегда можно разложить на произведение линейных и квадратных множителей, а многочлен четной степени — на произведение квадратных трехчленов.
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен 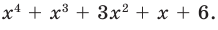
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
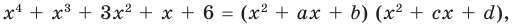 (3)
(3)
где  и
и  — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях
— неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях  у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
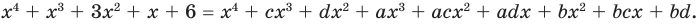
Получаем систему
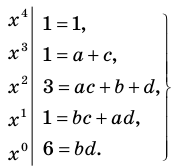 (4)
(4)
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 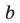 и
и 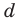 могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
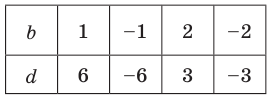
Коэффициенты  и
и  в равенстве (3) равноправны, поэтому мы не рассматриваем случаи
в равенстве (3) равноправны, поэтому мы не рассматриваем случаи  и
и 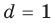 или
или 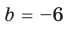 и
и 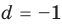 и т. д.
и т. д.
Для каждой пары значений  и
и 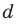 из третьего равенства системы (4) найдем
из третьего равенства системы (4) найдем 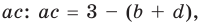 а из второго равенства имеем
а из второго равенства имеем 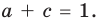 Зная
Зная 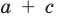 и
и 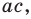 по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения
по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения  подставим в четвертое равенство системы (4)
подставим в четвертое равенство системы (4) 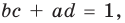 чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел 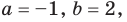
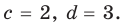 Тогда равенство (3) имеет вид
Тогда равенство (3) имеет вид
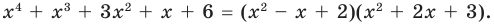 (5)
(5)
Поскольку квадратные трехчлены 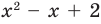 и
и 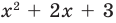 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 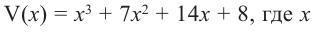 – положительное целое число и . Если высоты коробок можно определить при помощи линейной функции
– положительное целое число и . Если высоты коробок можно определить при помощи линейной функции 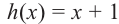 , то как можно выразить другие размеры коробки в виде многочлена? Вы сможете решить эту задачу, изучив правило деления многочлена на многочлен.
, то как можно выразить другие размеры коробки в виде многочлена? Вы сможете решить эту задачу, изучив правило деления многочлена на многочлен.
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 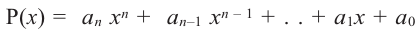 называется многочленом
называется многочленом 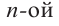 степени от одной переменной. Здесь
степени от одной переменной. Здесь 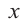 – переменная,
– переменная, 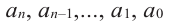 – определенные числа и
– определенные числа и 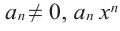 – старший член,
– старший член, 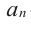 – коэффициент при старшем члене,
– коэффициент при старшем члене, 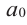 -свободный член. Многочлен можно разделить на многочлен аналогично правилу деления целых чисел столбиком.
-свободный член. Многочлен можно разделить на многочлен аналогично правилу деления целых чисел столбиком.
Деление целого числа па целое число можно проверить равенством
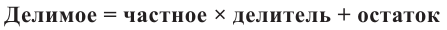
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 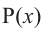 -делимое,
-делимое, 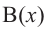 – делитель,
– делитель, 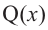 – неполное частное,
– неполное частное, 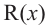 – остаток, то справедливо равенство
– остаток, то справедливо равенство
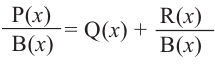 или
или 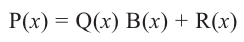 .
.
Здесь, степень многочлена 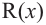 ниже степени многочлена
ниже степени многочлена 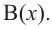 Если делителем является двучлен
Если делителем является двучлен 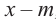 , то остатком может являться определенное число
, то остатком может являться определенное число 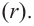
В этом случае: 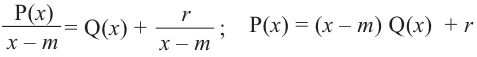
Пример №10
а) Разделите многочлен 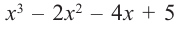 на двучлен
на двучлен 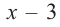 .
.
Ответ запишите в виде 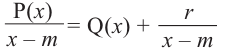
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
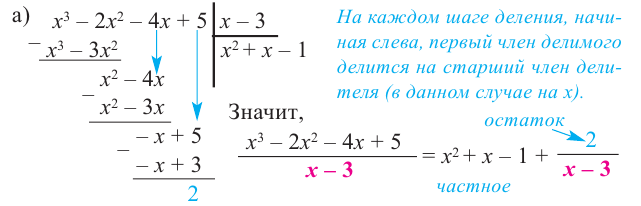
b) При этом  или
или  , иначе возникает деление на нуль.
, иначе возникает деление на нуль.
c) Должно выполняться тождество
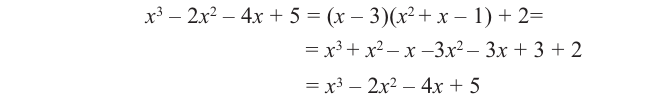
Пример №11
Разделите 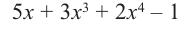 на многочлен
на многочлен 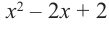 .
.
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0. 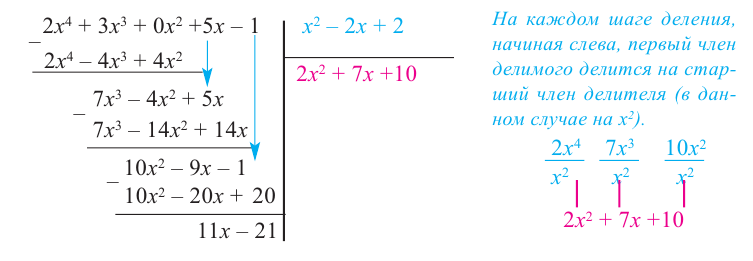
Пример №12
1) Исследуйте деление столбиком многочлена 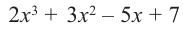 на двучлен
на двучлен 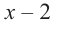 .
.
2) На каждом шаге деления делимое делится на старший член делителя, на 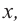 и результат записывается в частное. Установите, как можно найти первый член при делении на каждом из следующих шагов.
и результат записывается в частное. Установите, как можно найти первый член при делении на каждом из следующих шагов.
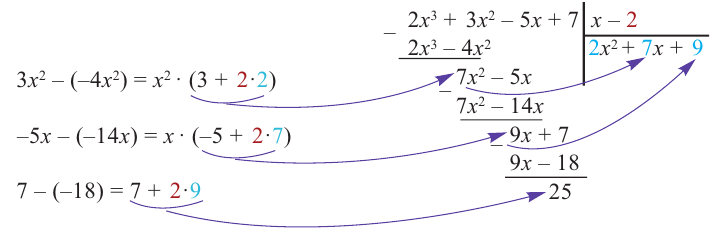 Правило синтетического деления многочлена на двучлен
Правило синтетического деления многочлена на двучлен 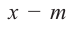 (схема Горнера)
(схема Горнера)
При делении многочлена на двучлен вида 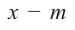 можно использовать метод, альтернативный делению столбиком – метод синтетического деления. При синтетическом делении, используя только коэффициенты, выполняется меньшее количество вычислений.
можно использовать метод, альтернативный делению столбиком – метод синтетического деления. При синтетическом делении, используя только коэффициенты, выполняется меньшее количество вычислений.
Пример №13
Разделите многочлен 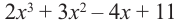 на двучлен
на двучлен 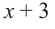 методом синтетического деления.
методом синтетического деления.
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 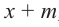 , то его записывают в виде
, то его записывают в виде 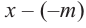 .
.
Запишем двучлен 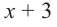 в виде
в виде 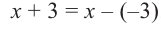 .
.
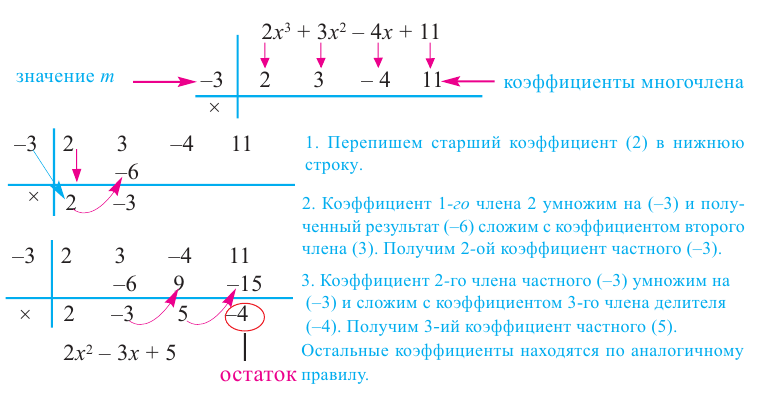
Таким образом, для делимого  и делителя
и делителя  частным будет
частным будет  , а остатком
, а остатком 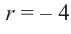 .
.
Деление можно записать в виде: 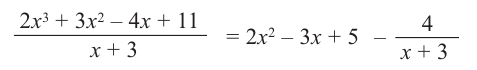 В общем случае, правило синтетического деления (или схема Горнера) многочлена и-ой степени на двучлен х -т приведено в таблице ниже.
В общем случае, правило синтетического деления (или схема Горнера) многочлена и-ой степени на двучлен х -т приведено в таблице ниже.
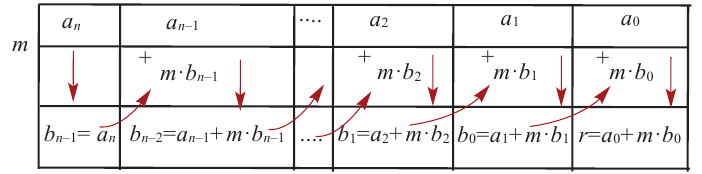
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 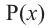 на двучлен
на двучлен 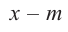 равен значению многочлена
равен значению многочлена 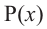 в точке
в точке 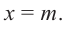
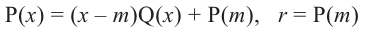
Доказательство: В равенстве 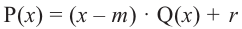 запишем
запишем 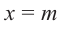 .
. 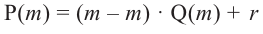 , тогда
, тогда 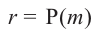 .
.
Пример №14
Найдите остаток от деления многочлена  на двучлен
на двучлен 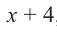 , применив теорему об остатке.
, применив теорему об остатке.
Решение: запишем делитель в виде 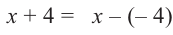 , тогда
, тогда 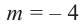 . По теореме об остатке получим, что остаток равен
. По теореме об остатке получим, что остаток равен 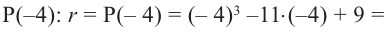
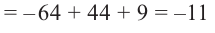 .
.
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 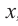 , которые обращают многочлен
, которые обращают многочлен 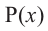 в нуль (т.е. корни уравнения
в нуль (т.е. корни уравнения 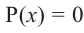 ), называются корнями (или нулями) многочлена.
), называются корнями (или нулями) многочлена.
Теорема. Если число 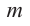 является корнем многочлена
является корнем многочлена 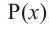 , то двучлен
, то двучлен 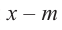 является множителем многочлена
является множителем многочлена 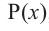 .
.
Действительно, если 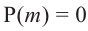 , то из равенства
, то из равенства 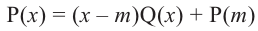 имеем
имеем 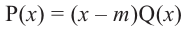 . Верно и обратное утверждение, т.е. если двучлен
. Верно и обратное утверждение, т.е. если двучлен 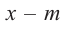 является множителем многочлена
является множителем многочлена 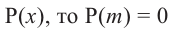 .
.
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 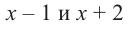 множителями многочлена
множителями многочлена 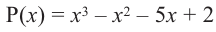 .
.
Решение: вычислим значение многочлена 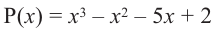 при
при 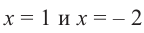 .
.
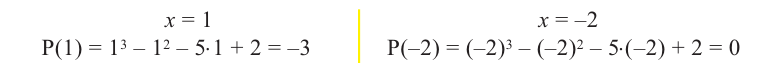
Значит, 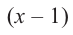 не является множителем, а
не является множителем, а 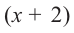 является одним из множителей данного многочлена.
является одним из множителей данного многочлена.
Пример №16
Зная, что 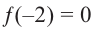 , разложите многочлен
, разложите многочлен 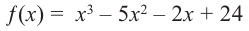 на множители.
на множители.
Решение: так как 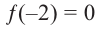 , то двучлен
, то двучлен 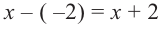 один из множителей многочлена
один из множителей многочлена . Другой множитель найдем, используя метод синтетического деления.
. Другой множитель найдем, используя метод синтетического деления.
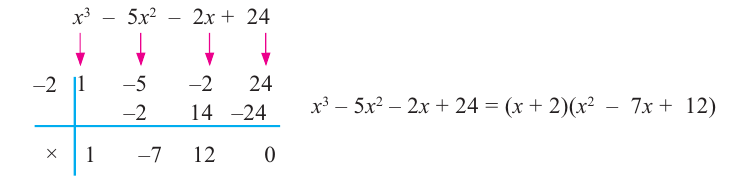
Учитывая, что 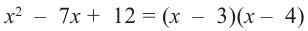 получим:
получим: 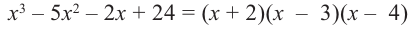 .
.
Отсюда получаем, что 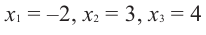 являются нулями многочлена.
являются нулями многочлена.
Примечание: Если многочлен задан в виде 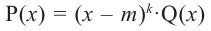 (здесь
(здесь 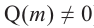 ), то число
), то число 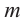 является
является 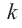 кратным корнем многочлена
кратным корнем многочлена 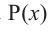 (повторяется
(повторяется 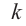 раз). Например, если разложение многочлена на множители имеет вид
раз). Например, если разложение многочлена на множители имеет вид 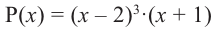 , то число
, то число 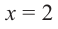 является корнем кратности 3.
является корнем кратности 3.
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 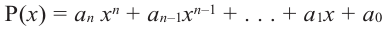 с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
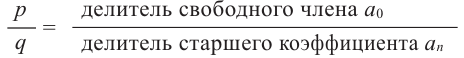
Доказательство. Пусть несократимая дробь 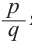 является корнем многочлена
является корнем многочлена 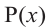 с целыми коэффициентами:
с целыми коэффициентами:
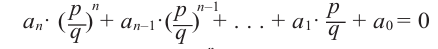
Умножим обе части равенства на 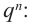
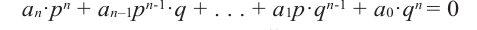
Так как в последнем равенстве каждый член, кроме члена 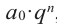 , содержит множитель
, содержит множитель  и каждый член, кроме члена
и каждый член, кроме члена  , содержит множитель
, содержит множитель 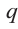 .то коэффициент
.то коэффициент 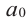 должен делится на
должен делится на 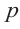 , а коэффициент
, а коэффициент 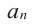 должен делится на
должен делится на 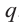 .
.
Пример №17
Найдите рациональные корни многочлена 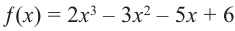 .
.
Решение: свободный член 6, старший коэффициент 2.
Для 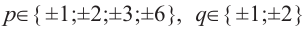 , запишем все возможные числа вида
, запишем все возможные числа вида 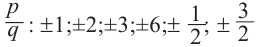
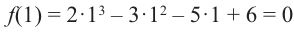 , т.е. одним из множителей является двучлен
, т.е. одним из множителей является двучлен  . Другие множители найдем, используя синтетическое деление:
. Другие множители найдем, используя синтетическое деление: 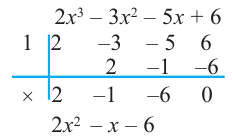
Так как, 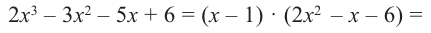
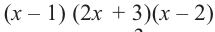 , получим, что
, получим, что 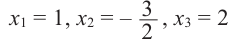 являются корнями многочлена.
являются корнями многочлена.
Следствие 1. Если старший коэффициент 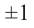 и многочлен имеет рациональный корень, то он является целым числом.
и многочлен имеет рациональный корень, то он является целым числом.
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена 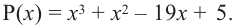
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
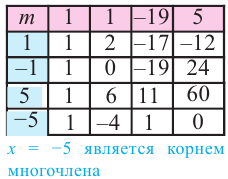
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 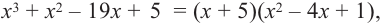 то, решив квадратное уравнение
то, решив квадратное уравнение 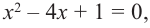 получим другие корни:
получим другие корни: 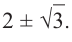 Значит данный многочлен третьей степени имеет три корня:
Значит данный многочлен третьей степени имеет три корня: 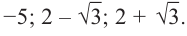
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 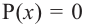 сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми. Например, для нахождения корней многочлена
сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми. Например, для нахождения корней многочлена
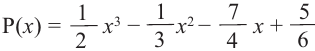 надо умножить все члены уравнения
надо умножить все члены уравнения 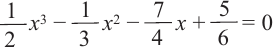 на 12, а затем решить полученное
на 12, а затем решить полученное
уравнение 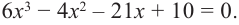
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 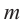 (обращающее значение многочлена в нуль), которое является корнем многочлена, т. е. определяется двучлен
(обращающее значение многочлена в нуль), которое является корнем многочлена, т. е. определяется двучлен 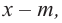 на который многочлен делится без остатка.
на который многочлен делится без остатка.
3. Для данного многочлена при помощи синтетического деления на двучлен 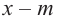 определяется другой множитель.
определяется другой множитель.
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 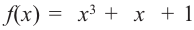 могут являться числа ±1.
могут являться числа ±1.
Проверим: 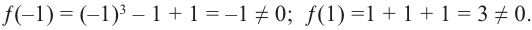 Значит, многочлен
Значит, многочлен 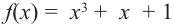 не имеет рациональных корней.
не имеет рациональных корней.
Основная теорема алгебры
Покажем на примере, что многочлен  ой степени имеет
ой степени имеет 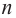 корней.
корней.
Пример №19
Найдите все корни многочлена 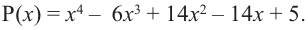
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
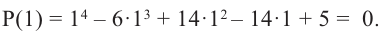
Значит, 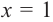 является корнем данного многочлена
является корнем данного многочлена 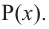 Другие корни найдем синтетическим делением.
Другие корни найдем синтетическим делением.
В выражении  для множителя
для множителя  вновь применим теорему о рациональных корнях и синтетическое деление. Тогда
вновь применим теорему о рациональных корнях и синтетическое деление. Тогда 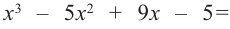
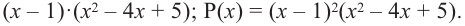 Решим уравнение
Решим уравнение 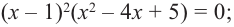
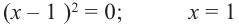 ( корень кратности 2);
( корень кратности 2);
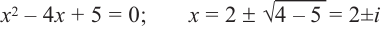
Корни: 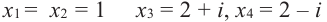
Во всех рассмотренных нами примерах уравнение  ой степени всегда имеет
ой степени всегда имеет  корней, включая кратные корни (действительных или комплексных).
корней, включая кратные корни (действительных или комплексных).
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 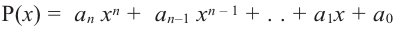 является многочленом ненулевой степени с комплексными коэффициентами, то согласно основной теореме алгебры, у него есть хотя бы один корень
является многочленом ненулевой степени с комплексными коэффициентами, то согласно основной теореме алгебры, у него есть хотя бы один корень 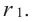 По теореме о разложении многочлена на множители получим
По теореме о разложении многочлена на множители получим 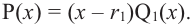 При этом многочлен
При этом многочлен 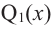 имеет степень
имеет степень 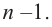 Если
Если 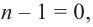 то
то 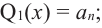 если
если 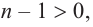 то согласно той же теореме, многочлен
то согласно той же теореме, многочлен 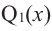 имеет хотя бы один корень. Обозначим его через
имеет хотя бы один корень. Обозначим его через 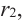 тогда справедливо разложение
тогда справедливо разложение 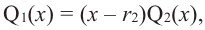 где
где 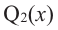 – многочлен степени
– многочлен степени 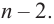 Значит, можно записать
Значит, можно записать 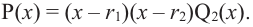 Аналогично, если
Аналогично, если 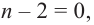 то
то 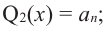 при
при 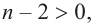 на основании той же теоремы, многочлен
на основании той же теоремы, многочлен 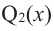 имеет хотя бы один корень. Обозначим его через
имеет хотя бы один корень. Обозначим его через 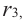 получим
получим 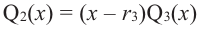 т. е. можно записать
т. е. можно записать 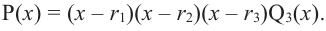
Продолжая процесс 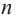 раз, получаем
раз, получаем  Тогда для многочлена
Тогда для многочлена 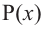 можно записать следующее разложение:
можно записать следующее разложение:
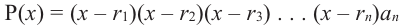
здесь числа  являются нулями многочлена
являются нулями многочлена  Эти нули могут и не быть различными.
Эти нули могут и не быть различными.
Следствие. Многочлен  ой степени
ой степени  на множестве комплексных чисел имеет ровно
на множестве комплексных чисел имеет ровно 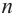 корней, включая кратные корни.
корней, включая кратные корни.
Отметим, что если комплексное число 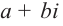 является корнем многочлена с действительными коэффициентами, то сопряженное комплексное число
является корнем многочлена с действительными коэффициентами, то сопряженное комплексное число 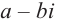 гак же является корнем данного многочлена.
гак же является корнем данного многочлена.
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 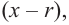 соответствующих действительным корням, и трехчленов вида
соответствующих действительным корням, и трехчленов вида 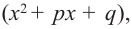 соответствующих сопряженным комплексным корням.
соответствующих сопряженным комплексным корням.
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и 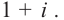
Решение: так как число 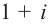 является корнем многочлена, то сопряженное комплексное число
является корнем многочлена, то сопряженное комплексное число 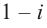 также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде
также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде
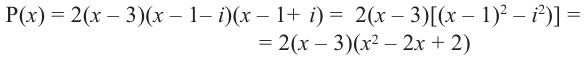
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 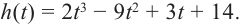 В какие моменты в течении 5 секунд после начала движения кабина карусели находилась на нулевом уровне?
В какие моменты в течении 5 секунд после начала движения кабина карусели находилась на нулевом уровне?
Решение: во всех случаях, кроме значений 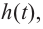 равных нулю, кабина карусели находится либо ниже, либо выше нулевого уровня. Значит, мы должны найти корни заданного многочлена. Применим правило нахождения рациональных корней.
равных нулю, кабина карусели находится либо ниже, либо выше нулевого уровня. Значит, мы должны найти корни заданного многочлена. Применим правило нахождения рациональных корней.
1. Проверим, является ли число  корнем.
корнем.
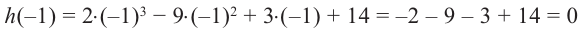
2. Число 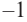 является корнем, значит одним из множителей данного многочлена является
является корнем, значит одним из множителей данного многочлена является 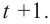 Другие корни найдем при помощи синтетического деления.
Другие корни найдем при помощи синтетического деления.
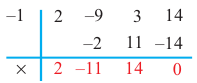
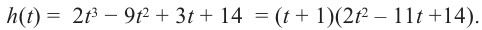
Учитывая, что 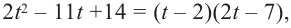 запишем многочлен в виде
запишем многочлен в виде 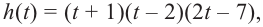 т. е.
т. е. 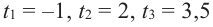 являются корнями уравнения. Значения
являются корнями уравнения. Значения 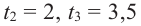 принадлежат временному интервалу в 5 секунд, и в этих моментах кабина карусели находилась на нулевом уровне. То, что корни найдены верно показывает график многочлена, построенный при помощи графкалькулягора.
принадлежат временному интервалу в 5 секунд, и в этих моментах кабина карусели находилась на нулевом уровне. То, что корни найдены верно показывает график многочлена, построенный при помощи графкалькулягора.
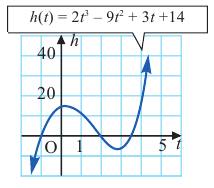
Функция-многочлен
График функции-многочлен
В стандартном виде функция – многочлен записывается как 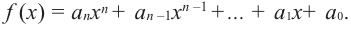 В частном случае, при
В частном случае, при  получаем линейную функцию (график – прямая линия), при
получаем линейную функцию (график – прямая линия), при  получаем квадратичную функцию (график- парабола). Любой многочлен определен на множестве действительных чисел и его графиком является непрерывная (сплошная) линия.
получаем квадратичную функцию (график- парабола). Любой многочлен определен на множестве действительных чисел и его графиком является непрерывная (сплошная) линия.
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 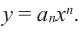 Ниже показаны примеры графиков функции – многочлен и их свойства.
Ниже показаны примеры графиков функции – многочлен и их свойства.
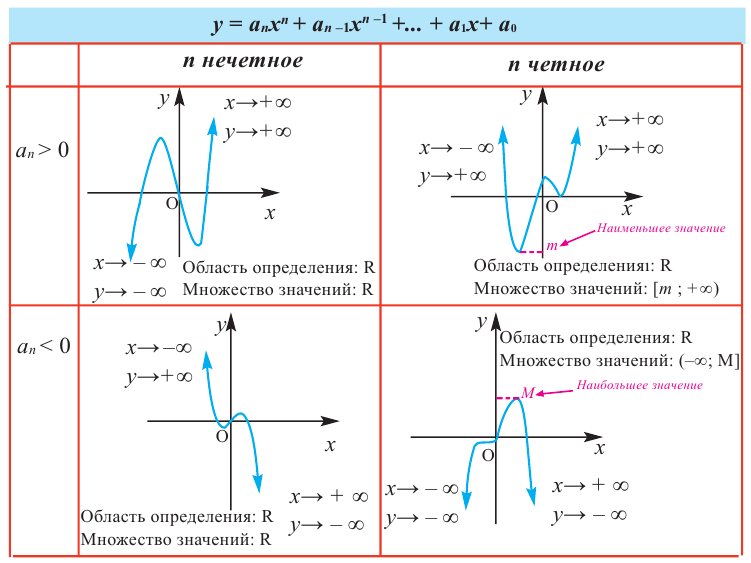
Пример №22
Определите характер поведения функции – многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 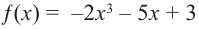 б)
б) 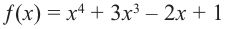
Решение: а) степень многочлена 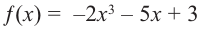 нечетная (равна 3). Коэффициент старшего члена равен
нечетная (равна 3). Коэффициент старшего члена равен 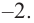 По таблице видно, что в данном случае при
По таблице видно, что в данном случае при 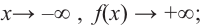 а при
а при 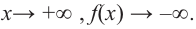
b) степень многочлена 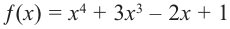 четная (равна 4). Коэффициент старшего члена равен 1. В данном случае при
четная (равна 4). Коэффициент старшего члена равен 1. В данном случае при 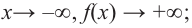 при
при 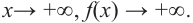
Пример №23
По графику определите как ведет себя функция – многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
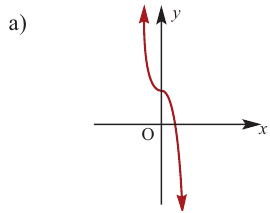
Решение:
при 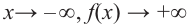
при 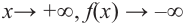
Многочлен нечетной степени
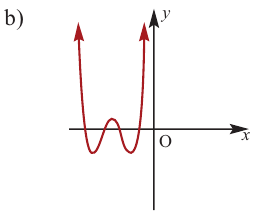
Решение:
при 
при 
Многочлен четной степени
Отметим, что если 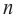 нечетно, то функция – многочлен имеет хотя бы один действительный нуль, если
нечетно, то функция – многочлен имеет хотя бы один действительный нуль, если 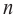 четно, то их вообще может и не быть.
четно, то их вообще может и не быть.
Алгоритм построения эскиза графика функции – многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции 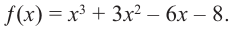
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа 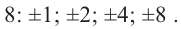
Проверим 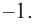
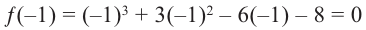
Значит, двучлен  является одним из множителей. Остальные множители найдем синтетическим делением.
является одним из множителей. Остальные множители найдем синтетическим делением.
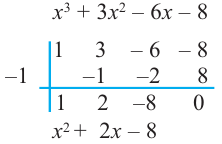
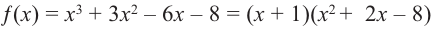
Зная, что 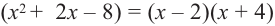 запишем все линейные множители многочлена:
запишем все линейные множители многочлена: 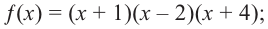
Отсюда находим нули 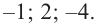 Т. е. график пересекает ось абсцисс в точках
Т. е. график пересекает ось абсцисс в точках 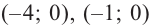 и
и 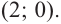 Так как
Так как 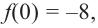 то точка
то точка 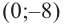 является точкой пересечения с осью
является точкой пересечения с осью 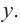 Отметим эти точки на координатной плоскости.
Отметим эти точки на координатной плоскости.
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 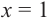 и
и 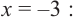
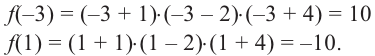
Отметим точки 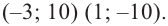
3. Определим, как меняется график при уменьшении или увеличении значений  Степень при старшем члене равна 3, а коэффициент положителен, функция нечетная. Значит, при
Степень при старшем члене равна 3, а коэффициент положителен, функция нечетная. Значит, при  при
при 
4. Соединим отмеченные точки и получим схематический график функции 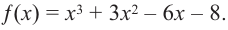
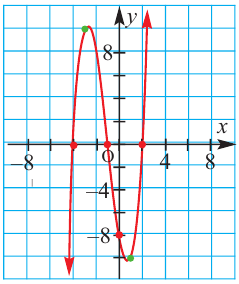
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
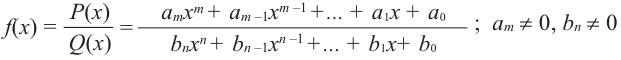
Самым простым примером рациональной функции является функция 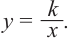
График функции 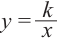 называется гиперболой.
называется гиперболой.
При стремлении значений  к нулю точки гиперболы стремятся к оси ординат, т е. к прямой
к нулю точки гиперболы стремятся к оси ординат, т е. к прямой  при неограниченном увеличении
при неограниченном увеличении 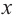 но абсолютному значению точки гиперболы неограниченно приближаются к оси абсцисс, т. е. к прямой
но абсолютному значению точки гиперболы неограниченно приближаются к оси абсцисс, т. е. к прямой 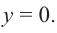 Прямая
Прямая  называется вертикальной асимптотой, а прямая
называется вертикальной асимптотой, а прямая 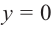 называется горизонтальной асимптотой гиперболы
называется горизонтальной асимптотой гиперболы 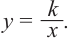 При параллельном переносе гиперболы
При параллельном переносе гиперболы 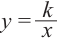 на вектор
на вектор  получается график функции
получается график функции 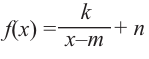 . В этом случае начало координат преобразуется в точку
. В этом случае начало координат преобразуется в точку  и вертикальной асимптотой становится прямая
и вертикальной асимптотой становится прямая 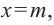 а горизонтальной- прямая
а горизонтальной- прямая 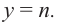
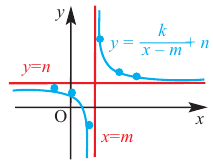
Пример №25
Постройте график функции 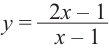
Решение: точки пересечения с осью 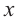 найдем из уравнения
найдем из уравнения 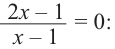
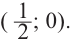
При 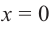 получим
получим 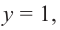 и график пересекает ось
и график пересекает ось  в точке
в точке  Разделим почленно числитель функции на знаменатель и запишем ее в виде
Разделим почленно числитель функции на знаменатель и запишем ее в виде 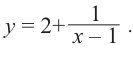 Прямая
Прямая 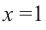 является вертикальной асимптотой, а прямая
является вертикальной асимптотой, а прямая 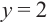 – горизонтальной асимптотой. Зададим таблицу значений для нескольких точек справа и слева от вертикальной асимптоты
– горизонтальной асимптотой. Зададим таблицу значений для нескольких точек справа и слева от вертикальной асимптоты
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках  и
и 
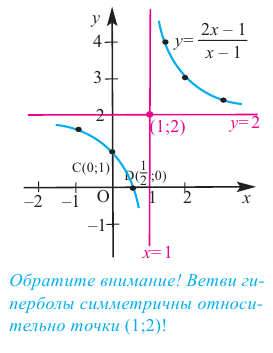
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 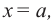 а числитель отличен от нуля, то данная функция имеет вертикальную асимптоту. Горизонтальные асимптоты для рациональной функции
а числитель отличен от нуля, то данная функция имеет вертикальную асимптоту. Горизонтальные асимптоты для рациональной функции 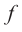 определяются в соответствии со степенью
определяются в соответствии со степенью  и
и  данных многочленов
данных многочленов 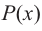 и
и 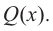
Для 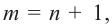 т. е. если степень многочлена в числителе на 1 единицу больше степени многочлена в знаменателе, частное, полученное при делении, имеет вид
т. е. если степень многочлена в числителе на 1 единицу больше степени многочлена в знаменателе, частное, полученное при делении, имеет вид 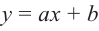 и является линейной функцией. При возрастании
и является линейной функцией. При возрастании  по абсолютному значению график функции приближается к данной прямой. В этом случае говорят, что прямая
по абсолютному значению график функции приближается к данной прямой. В этом случае говорят, что прямая 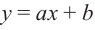 является наклонной асимптотой.
является наклонной асимптотой.
Пример №26
Найдите асимптоты и схематично изобразите график функции
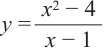
Решение: Точки пересечения с осью  найдем из уравнения
найдем из уравнения  При
При 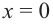 получим
получим 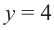 и график пересекает ось
и график пересекает ось  в точке
в точке  При
При 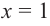 знаменатель обращается в нуль, а числитель отличен от нуля. Значит, прямая
знаменатель обращается в нуль, а числитель отличен от нуля. Значит, прямая 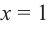 является вертикальной асимптотой. Горизонтальной асимптоты у данной функции нет
является вертикальной асимптотой. Горизонтальной асимптоты у данной функции нет  Разделив числитель на знаменатель, запишем функцию в виде:
Разделив числитель на знаменатель, запишем функцию в виде:
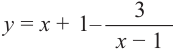
Для больших, но модулю, значений 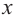 дробь
дробь 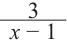 по абсолютному значению уменьшается и график заданной функции бесконечно приближается к прямой
по абсолютному значению уменьшается и график заданной функции бесконечно приближается к прямой 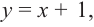 т. е. прямая
т. е. прямая 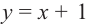 является наклонной асимптотой данной функции. Составим таблицу значений для некоторых точек слева и справа от вертикальной оси.
является наклонной асимптотой данной функции. Составим таблицу значений для некоторых точек слева и справа от вертикальной оси.
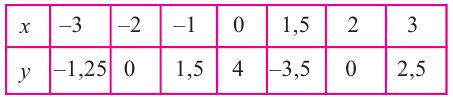
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
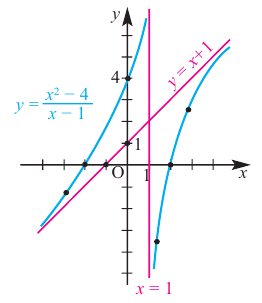
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
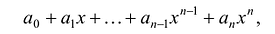 , где
, где 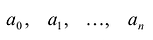 – действительные или комплексные числа, называемые коэффициентами, n – натуральное число, х – переменная величина, принимающая произвольные числовые значения.
– действительные или комплексные числа, называемые коэффициентами, n – натуральное число, х – переменная величина, принимающая произвольные числовые значения.
Если коэффициент 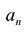 при
при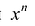 многочлена
многочлена 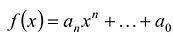 отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число n называется степенью многочлена,
отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число n называется степенью многочлена, 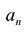 – старшим коэффициентом, а
– старшим коэффициентом, а 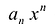 – старшим членом многочлена. Коэффициент
– старшим членом многочлена. Коэффициент 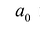 называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 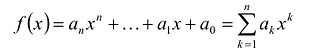 и
и 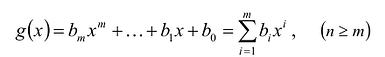 называется многочлен
называется многочлен
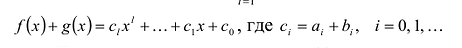
Произведением многочленов 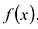 и
и  называется многочлен:
называется многочлен: 
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 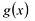 называется делителем многочлена
называется делителем многочлена 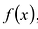 , если существует многочлен
, если существует многочлен 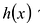 такой, что
такой, что 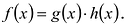
Теорема о делении с остатком
Для любых многочленов 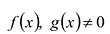 существуют многочлены
существуют многочлены 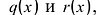 такие, что
такие, что 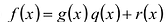 причем степень
причем степень 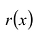 меньше степени g(x) или
меньше степени g(x) или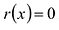 . Многочлены g(x) и r(x) определены однозначно.
. Многочлены g(x) и r(x) определены однозначно.
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит  , то остаток
, то остаток 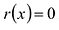 .
.
Число с называется корнем многочлена  , если
, если  .
.
Теорема Безу
Число с является корнем многочлена  тогда и только тогда, когда
тогда и только тогда, когда  делится на x – с.
делится на x – с.
Пусть с – корень многочлена  , т.е.
, т.е. . Разделим
. Разделим  на
на
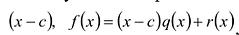 где степень r(х) меньше степени (x-с) которая равна 1. Значит, степень г(х) равна 0, т.е. r(х) = const. Значит,
где степень r(х) меньше степени (x-с) которая равна 1. Значит, степень г(х) равна 0, т.е. r(х) = const. Значит, 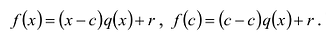 . Так как
. Так как  , то из последнего равенства следует, что r=0, т.е.
, то из последнего равенства следует, что r=0, т.е. 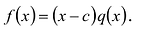
Обратно, пусть (х-с) делит  , т.е.
, т.е. 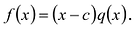 . Тогда
. Тогда 
Следствие. Остаток от деления многочлена  на (x-с) равен
на (x-с) равен  .
.
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена  равносильно разысканию его линейных делителей со старшим коэффициентом 1.
равносильно разысканию его линейных делителей со старшим коэффициентом 1.
Многочлен  можно разделить на линейный многочлен х-с с помощью алгоритма деления с остатком, но существует более удобный способ деления, известный под названием схемы Горнера.
можно разделить на линейный многочлен х-с с помощью алгоритма деления с остатком, но существует более удобный способ деления, известный под названием схемы Горнера.
Пусть 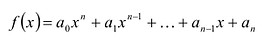 и пусть
и пусть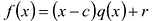 где
где 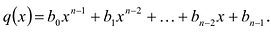 Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и правой частях последнего равенства, имеем:
Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и правой частях последнего равенства, имеем:
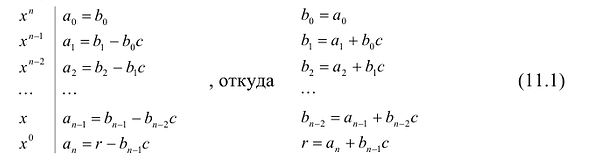
Число с-называется корнем кратности к многочлена  , если
, если 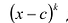 делит
делит  , но
, но 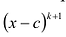 уже не делит
уже не делит  .
.
Чтобы поверить, будет ли число с корнем многочлена  и какой кратности, можно воспользоваться схемой Горнера. Сначала
и какой кратности, можно воспользоваться схемой Горнера. Сначала  делится на х-с, затем, если остаток равен нулю, полученное частное делится на х-с, и т.д. до получения не нулевого остатка.
делится на х-с, затем, если остаток равен нулю, полученное частное делится на х-с, и т.д. до получения не нулевого остатка.
Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени  имеет в С (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.
имеет в С (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.

где  – корни
– корни  , т.е. во множестве С всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то:
, т.е. во множестве С всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то: 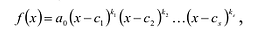 где
где 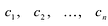 уже различные корни
уже различные корни  ,
,  – кратность корня
– кратность корня 
Если многочлен 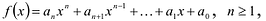 , с действительными коэффициентами имеет корень с, то число с также корень
, с действительными коэффициентами имеет корень с, то число с также корень 
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 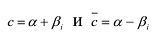 корни
корни  Тогда
Тогда  делится на х-с и
делится на х-с и 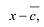 , но так как у
, но так как у 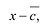 и х-с, нет общих делителей, то
и х-с, нет общих делителей, то  делится на произведение
делится на произведение 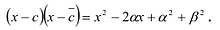
Утверждение 2. Многочлен с действительными коэффициентами степени 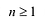 всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где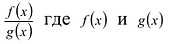 многочлены с действительными коэффициентами, причем многочлен
многочлены с действительными коэффициентами, причем многочлен 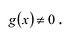 Рациональная дробь
Рациональная дробь  называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде
называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде 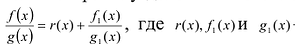 некоторые многочлены, а
некоторые многочлены, а 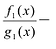 правильная рациональная дробь.
правильная рациональная дробь.
Лемма 1, Если  правильная рациональная дробь, а число
правильная рациональная дробь, а число  является вещественным корнем кратности
является вещественным корнем кратности  многочлена
многочлена 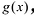 , т.е.
, т.е.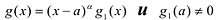 , то существует вещественное число A и многочлен
, то существует вещественное число A и многочлен  с вещественными коэффициентами, такие, что
с вещественными коэффициентами, такие, что 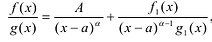 где дробь
где дробь 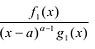 является правильной.
является правильной.
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если  правильная рациональная дробь, а число
правильная рациональная дробь, а число является корнем кратности
является корнем кратности  многочлена g(x), т.е.
многочлена g(x), т.е.  и если
и если 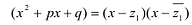 , то существуют вещественные числа M и N многочлен
, то существуют вещественные числа M и N многочлен 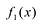 с вещественными коэффициентами, такие,
с вещественными коэффициентами, такие,  где дробь ,
где дробь ,  также является правильной.
также является правильной.
Рациональные дроби вида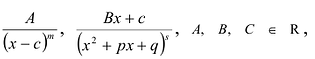
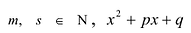 – трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
– трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 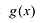 равна n, то в числителе после приведения к общему знаменателю получается многочлен степени n-1, т.е. многочлен
равна n, то в числителе после приведения к общему знаменателю получается многочлен степени n-1, т.е. многочлен  коэффициентами.
коэффициентами.
Число неизвестных 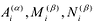 ‘ также равняется n:
‘ также равняется n: 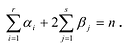
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение

