Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.
Для чтения этой темы желательно, хоть и не обязательно, ознакомиться с темой “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи”, а также с темой “Базисные и свободные переменные. Общее и базисное решения системы линейных алгебраических уравнений”.
Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.
Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи” вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $left { begin{aligned}
& 2x_1-3x_2-x_3-x_4=0;\
& -4x_1+5x_2+3x_4=0.
end{aligned} right.$ является однородной, так как все свободные члены этой системы (т.е. числа, стоящие в правых частях равенств) – нули.
Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:
$$
left { begin{aligned}
& 2cdot 0-3cdot 0-0-0=0;\
& -4cdot 0+5cdot 0+3cdot 0=0.
end{aligned} right.
$$
Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?
Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:
$$
left { begin{aligned}
& 2cdot 1-3cdot (-1)-2-3=0;\
& -4cdot 1+5cdot (-1)+3cdot 3=0.
end{aligned} right.
$$
Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.
Кстати сказать, чтобы не писать каждый раз выражения вроде “$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$”, пишут все значения переменных в матрицу-столбец: $left(begin{array} {c}
1 \
-1 \
2 \
3 end{array} right)$. Эту матрицу тоже называют решением СЛАУ.
Теорема Кронекера-Капелли гласит, что любая СЛАУ имеет решение (совместна) тогда и только тогда, когда ранг матрицы системы ($A$) равен рангу расширенной матрицы системы ($widetilde{A}$), т.е. $rang A=rangwidetilde{A}$. Так как мы уже выяснили, что любая однородная СЛАУ имеет решение (хотя бы одно), то для всех однородных СЛАУ $rang A=rangwidetilde{A}$. Так как ранги равны между собой, то можно обозначить их какой-то одной буквой, например, $r$. Итак, для любой однородной СЛАУ имеем: $rang A=rangwidetilde{A}=r$.
Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.
Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.
Этот случай уже был рассмотрен в теме “Базисные и свободные переменные. Общее и базисное решения СЛАУ”. По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.
Что такое базисные и свободные переменные? показатьскрыть
Фундаментальная система решений однородной СЛАУ.
С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $varphi_1$, $varphi_2$,…, $varphi_{n-r}$.
Любая совокупность $n-r$ линейно независимых решений однородной СЛАУ называется фундаментальной системой (или совокупностью) решений данной СЛАУ.
Часто вместо словосочетания “фундаментальная система решений” используют аббревиатуру “ФСР”. Если решения $varphi_1$, $varphi_2$,…, $varphi_{n-r}$ образуют ФСР, и $X$ – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:
$$
X=C_1cdot varphi_1+C_2cdot varphi_2+ldots+C_{n-r}cdot varphi_{n-r},
$$
где $C_1$, $C_2$,…, $C_{n-r}$ – произвольные постоянные.
Что значит “линейно независимые решения”? показатьскрыть
Пример №1
Решить СЛАУ
$$left { begin{aligned}
& 3x_1-6x_2+9x_3+13x_4=0\
& -x_1+2x_2+x_3+x_4=0;\
& x_1-2x_2+2x_3+3x_4=0.
end{aligned} right.$$
Если система является неопределённой, указать фундаментальную систему решений.
Решение
Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$
left( begin{array} {cccc|c}
3 & -6 & 9 & 13 & 0 \
-1 & 2 & 1 & 1 & 0 \
1 & -2 & 2 & 3 & 0 end{array} right) rightarrow
left|begin{aligned}
& text{поменяем местами первую и третью}\
& text{строки, чтобы первым элементом}\
& text{первой строки стала единица.}
end{aligned}right| rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
-1 & 2 & 1 & 1 & 0 \
3 & -6 & 9 & 13 & 0
end{array} right)
begin{array} {l} phantom{0} \ r_2+r_1\ r_3-3r_1end{array} rightarrow
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0 \
0 & 0 & 3 & 4 & 0
end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\ r_3-r_2end{array} rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0 \
0 & 0 & 0 & 0 & 0
end{array}right).
$$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde{A} = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на “ступеньках”. Что это за “ступеньки” показано на рисунке:

На “ступеньках” стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Примечание. показатьскрыть
Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0 \
0 & 0 & 0 & 0 & 0
end{array}right)$ от нулевой строки:
$$
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 0\
0 & 0 & 3 & 4 & 0
end{array}right)
$$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$
left( begin{array} {cc|cc}
1 & 2 & 2 & -3\
0 & 3 & 0 & -4
end{array}right)
begin{array} {l} phantom{0} \ 1/3cdot{r_2} end{array} rightarrow
left( begin{array} {cc|cc}
1 & 2 & 2 & -3\
0 & 1 & 0 & -4/3
end{array}right)
begin{array} {l} r_1-2r_2 \ phantom{0} end{array} rightarrow \
rightarrow left(begin{array} {cc|cc}
1 & 0 & 2 & -1/3\
0 & 1 & 0 & -4/3
end{array}right).
$$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:
$$
left{begin{aligned}
& x_1=2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.
$$
Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-frac{1}{3}x_4$ и $x_3=-frac{4}{3}x_4$ в левую часть первого уравнения, получим:
$$
3x_1-6x_2+9x_3+13x_4=3cdot left(2x_2-frac{1}{3}x_4right)-6x_2+9cdot left(-frac{4}{3}x_4right)+13x_4=0.
$$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $left(begin{array} {cc} 1 & 0 \0 & 1end{array}right)$. Таблица будет выглядеть так:

Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-frac{1}{3}x_4$ и $x_3=-frac{4}{3}x_4$. Если $x_2=1$, $x_4=0$, то:
$$
begin{aligned}
& x_1=2cdot 1-frac{1}{3}cdot 0=2;\
& x_3=-frac{4}{3}cdot 0=0.
end{aligned}
$$
Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:
$$
begin{array} {c|c|c|c}
x_1 & x_3 & x_2 & x_4 \
hline 2 & 0 & 1 & 0 \
hline & & 0 & 1
end{array}
$$
Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:
$$
begin{aligned}
& x_1=2cdot 0-frac{1}{3}cdot 1=-frac{1}{3};\
& x_3=-frac{4}{3}cdot 1=-frac{4}{3}.
end{aligned}
$$
Найденные значения $x_1=-frac{1}{3}$ и $x_3=-frac{4}{3}$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:
$$
begin{array} {c|c|c|c}
x_1 & x_3 & x_2 & x_4 \
hline 2 & 0 & 1 & 0 \
hline -frac{1}{3} & -frac{4}{3} & 0 & 1
end{array}
$$
Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=left(begin{array} {c} x_1 \x_2 \x_3 \x_4 end{array}right)$. В том же порядке, в котором в матрице $X$ перечислены переменные, записываем значения переменных из таблицы в две матрицы:
$$
varphi_1=left(begin{array} {c} 2 \1 \0 \0 end{array}right);;
varphi_2=left(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right).
$$
Совокупность $varphi_1=left(begin{array} {c} 2 \1 \0 \0 end{array}right)$, $varphi_2=left(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$
X=C_1cdotleft(begin{array} {c} 2 \1 \0 \0 end{array}right)+C_2cdotleft(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right),
$$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Общее решение: $left{begin{aligned}
& x_1=2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.$. Или так: $X=C_1cdotleft(begin{array} {c} 2 \1 \0 \0 end{array}right)+C_2cdotleft(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right)$, где $C_1$ и $C_2$ – произвольные константы. Фундаментальная система решений: $varphi_1=left(begin{array} {c} 2 \1 \0 \0 end{array}right)$, $varphi_2=left(begin{array} {c} -1/3 \0 \ -4/3 \1 end{array}right)$.
Пример №2
Записать ФСР однородной СЛАУ
$$
left{begin{aligned}
& x_1-5x_2-x_3-2x_4+3x_5=0;\
& 2x_1-6x_2+x_3-4x_4-2x_5=0; \
& -x_1+4x_2+5x_3-3x_4=0.
end{aligned} right.,
$$
зная общее решение. Записать общее решение с помощью ФСР.
Решение
Общее решение уже было получено в теме “метод Крамера” (пример №4). Это решение таково:
$$
left{begin{aligned}
& x_1=frac{-17x_4+144x_5}{19};\
& x_2=frac{-15x_4+41x_5}{19};\
& x_3=frac{20x_4-4x_5}{19}; \
& x_4in R; ; x_5in R.
end{aligned} right.
$$
Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.
Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.
Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.
$$
begin{array} {c|c|c|c|c}
x_1 & x_2 & x_3 & x_4 & x_5\
hline -frac{17}{19} & -frac{15}{19} & frac{20}{19} & 1 & 0 \
hline frac{144}{19} & frac{41}{19} & -frac{4}{19} & 0 & 1
end{array}
$$
Совокупность $varphi_1=left(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)$, $varphi_2=left(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$
X=C_1cdotleft(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)+C_2cdotleft(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right),
$$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Фундаментальная система решений: $varphi_1=left(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)$, $varphi_2=left(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right)$. Общее решение: $X=C_1cdotleft(begin{array} {c} -17/19 \-15/19 \20/19 \1\0 end{array}right)+C_2cdotleft(begin{array}{c} 144/19 \ 41/19 \ -4/19\0\1 end{array}right)$, где $C_1$ и $C_2$ – произвольные константы.
Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.
На чтение 1 мин Просмотров 152 Опубликовано 01.05.2013
Обновлено 30.01.2023
В ходе работы с цифровыми (и не только) сигналами часто необходимо найти нули и плюсы системы. Кстати буржуи зовут числитель numerator`ом,а знаменатель — denumerator`ом. Стоит знать это при работе с их материалами и справочной системой Matlab.
Ближе к делу. В матлаб можно очень просто найти нули и полюсы. Для этого вам необходима переменная со значениями коэффициентов полинома числителя и знаменателя.
num = 1; % числитель den = [1 -1]; % знаменатель
Т.е. вот такая дробь:
Ts = 1; % период семплов sys = tf(num,den,Ts); % дискретная система
Находим нули и полюсы:
P = pole(sys); % poles Z = zero(sys); % zeros
Выводим на экран на еденичную окружность:
zplane(P,Z);
Как видите вывелся только один полюс (1 — i0).
Похожий код:

Программист, разработчик с 5 летним опытом работы. Учусь на разработчика игр на Unity и разработчика VR&AR реальности (виртуальной реальности). Основные языки программирования: C#, C++.
Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.
Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.
Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи” вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $left < begin& 2x_1-3x_2-x_3-x_4=0;\ & -4x_1+5x_2+3x_4=0. end right.$ является однородной, так как все свободные члены этой системы (т.е. числа, стоящие в правых частях равенств) – нули.
Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:
Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?
Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:
Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.
Кстати сказать, чтобы не писать каждый раз выражения вроде “$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$”, пишут все значения переменных в матрицу-столбец: $left(begin 1 \ -1 \ 2 \ 3 end right)$. Эту матрицу тоже называют решением СЛАУ.
Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.
Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.
Этот случай уже был рассмотрен в теме “Базисные и свободные переменные. Общее и базисное решения СЛАУ”. По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.
Что такое базисные и свободные переменные? показатьскрыть
Прежде чем дать определение этим терминам, стоит вспомнить, что означает фраза “ранг матрицы равен $r$”. Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют. Теперь можно дать следующее определение:
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Фундаментальная система решений однородной СЛАУ.
С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $varphi_1$, $varphi_2$. $varphi_$.
Часто вместо словосочетания “фундаментальная система решений” используют аббревиатуру “ФСР”. Если решения $varphi_1$, $varphi_2$. $varphi_$ образуют ФСР, и $X$ – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:
$$ X=C_1cdot varphi_1+C_2cdot varphi_2+ldots+C_cdot varphi_, $$
где $C_1$, $C_2$. $C_$ – произвольные постоянные.
Что значит “линейно независимые решения”? показатьскрыть
В данной ситуации под решением понимается матрица-столбец, в которой перечислены значения неизвестных.
Решения $varphi_1$, $varphi_2$, $ldots$, $varphi_n$ называются линейно зависимыми, если существуют такие константы $alpha_1,;alpha_2,;alpha_3,ldots,alpha_n$, что выполняется следующее равенство:
$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+ldots+alpha_ncdot varphi_n=O $$
при условии, что среди коэффициентов $alpha_i$ есть хотя бы один, не равный нулю.
Если же указанное выше равенство возможно лишь при условии $alpha_1=alpha_2=ldots=alpha_n=0$, то система решений называется линейно независимой.
Буква “$O$” в данном определении обозначает нулевую матрицу. Проще всего пояснить это определение на конкретном примере. Давайте рассмотрим ту СЛАУ, о которой шла речь в начале темы. Мы уже проверили, что $varphi_1=left(begin 1 \-1 \2 \3 endright)$ – решение данной СЛАУ. Точно так же можно показать, что $varphi_2=left(begin 16 \ 11 \ -4 \ 3 endright)$, $varphi_3=left(begin -5 \ -4 \ 2 \ 0 endright)$, $varphi_4=left(begin 7 \ 5 \ -2 \ 1endright)$ – решения данной системы.
Примем $alpha_1=-1$, $alpha_2=0$, $alpha_3=4$, $alpha_4=3$. Выясним, чему же равно выражение $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4$:
$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4= -1cdot left(begin 1 \-1 \2 \3 endright)+ 0cdot left(begin 16 \ 11 \ -4 \ 3 endright)+ 4cdot left(begin -5 \ -4 \ 2 \ 0 endright)+ 3cdot left(begin 7 \ 5 \ -2 \ 1endright)=\ =left(begin -1+0-20+21\ 1+0-16+15 \ -2+0+8-6 \ -3+0+0+3endright)= left(begin 0\ 0\ 0\0endright). $$
Итак, существуют такие значения констант $alpha_1$, $alpha_2$, $alpha_3$, $alpha_4$, не все одновременно равные нулю, что выполняется равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4=O$. Вывод: совокупность решений $varphi_1$, $varphi_2$, $varphi_3$, $varphi_4$ – линейно зависима.
Для сравнения: равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2=O$ возможно лишь при условии $alpha_1=alpha_2=0$ (я не буду это доказывать, поверьте на слово 🙂 ). Следовательно, система $varphi_1$, $varphi_2$ является линейно независимой.
Если система является неопределённой, указать фундаментальную систему решений.
Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$ left( begin 3 & -6 & 9 & 13 & 0 \ -1 & 2 & 1 & 1 & 0 \ 1 & -2 & 2 & 3 & 0 end right) rightarrow left|begin & text<поменяем местами первую и третью>\ & text<строки, чтобы первым элементом>\ & text <первой строки стала единица.>endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ -1 & 2 & 1 & 1 & 0 \ 3 & -6 & 9 & 13 & 0 end right) begin phantom <0>\ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 3 & 4 & 0 endright) begin phantom <0>\ phantom<0>\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright). $$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на “ступеньках”. Что это за “ступеньки” показано на рисунке:
На “ступеньках” стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.
Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:
$$ M_<2>^<(1)>=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$
Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.
Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №2 и №4:
$$ M_<2>^<(2)>=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №2 (он соответствует переменной $x_2$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_2$ и $x_4$ можно принять в качестве базисных.
Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.
Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.
В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.
Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:
$$ left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright) $$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=0$, а вторая строка соответствует уравнению $3x_3+4x_4=0$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.
Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$ left( begin 1 & 2 & 2 & -3\ 0 & 3 & 0 & -4 endright) begin phantom <0>\ II:3 end rightarrow left( begin 1 & 2 & 2 & -3\ 0 & 1 & 0 & -4/3 endright) begin I-2cdot II \ phantom <0>end rightarrow \ rightarrow left(begin 1 & 0 & 2 & -1/3\ 0 & 1 & 0 & -4/3 endright). $$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:
Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-frac<1><3>x_4$ и $x_3=-frac<4><3>x_4$ в левую часть первого уравнения, получим:
$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(2x_2-frac<1><3>x_4right)-6x_2+9cdot left(-frac<4><3>x_4right)+13x_4=0. $$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $left(begin 1 & 0 \0 & 1endright)$. Таблица будет выглядеть так:
Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-frac<1><3>x_4$ и $x_3=-frac<4><3>x_4$. Если $x_2=1$, $x_4=0$, то:
Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:
Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:
Найденные значения $x_1=-frac<1><3>$ и $x_3=-frac<4><3>$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:
Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=left(begin x_1 \x_2 \x_3 \x_4 endright)$. В том же порядке, в котором в матрице $X$ перечислены переменные, записываем значения переменных из таблицы в две матрицы:
$$ varphi_1=left(begin 2 \1 \0 \0 endright);; varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright). $$
Совокупность $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$ X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright), $$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Общее решение: $left <begin& x_1=2x_2-frac<1><3>x_4;\ & x_2in R;\ & x_3=-frac<4><3>x_4;\ & x_4 in R. endright.$. Или так: $X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright)$, где $C_1$ и $C_2$ – произвольные константы. Фундаментальная система решений: $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$.
Записать ФСР однородной СЛАУ
зная общее решение. Записать общее решение с помощью ФСР.
Общее решение уже было получено в теме “метод Крамера” (пример №4). Это решение таково:
Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.
Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.
Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.
Совокупность $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$ X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright), $$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Фундаментальная система решений: $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$. Общее решение: $X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$, где $C_1$ и $C_2$ – произвольные константы.
Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -2<,>34 )
Ввод: -1,15
Результат: ( -1<,>15 )
Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac<2> <3>$$
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac<8> <3>$$
Помните, что на ноль делить нельзя!
RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :
Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_<11>x_1 + a_<12>x_2 + cdots + a_<1n>x_n = b_1 \ a_<21>x_1 + a_<22>x_2 + cdots + a_<2n>x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag <1>)
Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.
Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.
СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.
Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.
Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.
СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.
Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.
Формы записи СЛАУ
Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.
Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ <11>\ a_ <21>\ vdots \ a_ end x_1 + begin a_ <12>\ a_ <22>\ vdots \ a_ end x_2 + ldots + begin a_ <1n>\ a_ <2n>\ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag <2>)
Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.
Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).
Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.
Критерий совместности СЛАУ
“Триединство” форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).
Матрицу
( A = begin a_ <11>& a_ <12>& cdots & a_ <1n>\ a_ <21>& a_ <22>& cdots & a_ <2n>\ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ <11>& a_ <12>& cdots & a_ <1n>& b_1 \ a_ <21>& a_ <22>& cdots & a_ <2n>& b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.
Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).
Формулы Крамера
Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac<Delta_i> <|A|>;,quad i=overline <1,n>tag <3>$$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.
Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.
Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.
Однородные системы
Теорема. Если столбцы ( X^<(1)>, X^<(2)>, ldots , X^ <(s)>) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.
Естественно попытаться найти такие решения ( X^<(1)>, ldots , X^ <(s)>) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.
Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.
Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^<(1)>, ldots , X^ <(k)>) этой СЛАУ, образующих фундаментальную систему решений.
Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.
Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ <(1)>+ ldots + c_kX^ <(k)>$$
где постоянные ( c_i ;, quad i=overline <1,k>), принимают произвольные значения.
Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.
Неоднородные системы
Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).
Следствие. Пусть (X’) и (X”) — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ – X” ) является решением соответствующей однородной системы (AY=0).
Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.
Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^<(1)>, ldots , X^ <(k)>) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ <(1)>+ c_2 X^ <(2)>+ ldots + c_k X^ <(k)>$$
где ( c_i in mathbb ;, quad i=overline <1,k>).
Эту формулу называют общим решением СЛАУ.
Как решать систему уравнений

О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Решим систему уравнений методом подстановки
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Пример.
Домножим первое уравнение системы на -2, второе оставим без изменений. Система примет вид:
Сложим уравнения, получим
Отсюда y = -3, а, значит, x = 2
Ответ: (2; -3).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
[spoiler title=”источники:”]
http://www.math-solution.ru/math-task/slau
http://skysmart.ru/articles/mathematic/reshenie-sistem-uravnenij
[/spoiler]
Содержание:
- Однородные СЛАУ
- Фундаментальная система решений
Однородные СЛАУ
Определение
Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.
Однородная СЛАУ, записанная в
матричном виде, $A X=Theta$ всегда совместна,
так как $X=Theta$ всегда является ее решением.
Заметим, что если $x_{1}, x_{2}$ – это два решения однородной
СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:
$$Y=lambda_{1} x_{1}+lambda_{2} x_{2}$$
$$A Y=Aleft(lambda_{1} x_{1}+lambda_{2} x_{2}right)=lambda_{1} A x_{1}+lambda_{2} A x_{2}=lambda_{1} Theta+lambda_{2} Theta=Theta$$
Теорема
Если однородная квадратная СЛАУ имеет ненулевое решение, то
определитель матрицы системы равен нулю.
Пример
Задание. Выяснить, имеет ли однородная СЛАУ
$left{begin{array}{l}
3 x-2 y=-1 \
x+3 y=7
end{array}right.$ ненулевые решения.
Решение. Вычислим определитель матрицы системы:
$$Delta=left|begin{array}{rr}
3 & -2 \
1 & 3
end{array}right|=9-(-2)=9+2=11 neq 0$$
Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$
Ответ. Система имеет только нулевое решение.
Фундаментальная система решений
Рассмотрим множество всех столбцов, которые являются решениями исходной системы.
Определение
Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.
Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы.
Любое решение исходной системы есть линейная комбинация решений ФСР.
Теорема
Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и
общего решения соответствующей однородной СЛАУ.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти общее решение и ФСР однородной системы
$left{begin{array}{l}
x_{1}+x_{2}-3 x_{4}-x_{5}=0 \
x_{1}-x_{2}+2 x_{3}-x_{4}=0 \
4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \
2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0
end{array}right.$
Решение. Приведем систему к ступенчатому виду с помощью
метода Гаусса. Для этого записываем
матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец
свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут
получаться нули):
$$A=left(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
1 & -2 & 2 & -1 & 0 \
4 & -2 & 6 & 3 & -4 \
2 & 4 & -2 & 4 & -7
end{array}right)$$
с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем
первую, от третьей – четыре первых, от четвертой – две первых:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & -6 & 6 & 15 & 0 \
0 & 2 & -2 & 10 & -5
end{array}right)$$
Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три
вторых, к четвертой прибавляем вторую:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 9 & -3 \
0 & 0 & 0 & 12 & -4
end{array}right)$$
От четвертой строки отнимем $frac{4}{3}$ третьей и третью
строку умножим на $frac{1}{3}$ :
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1 \
0 & 0 & 0 & 0 & 0
end{array}right)$$
Нулевые строки можно далее не рассматривать, тогда получаем, что
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1
end{array}right)$$
Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а
ко второй строке прибавляем третью:
$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -6 & 0 \
0 & -2 & 2 & 5 & 0 \
0 & 0 & 0 & 3 & -1
end{array}right)$$
то есть получаем систему, соответствующую данной матрице:
$$left{begin{array}{l}
x_{1}+x_{2}-6 x_{4}=0 \
-2 x_{2}+2 x_{3}+5 x_{4}=0 \
3 x_{4}-x_{5}=0
end{array}right.$$
Или, выразив одни переменные через другие, будем иметь:
$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{2}=x_{2} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{4}=x_{4} \
x_{5}=3 x_{4}
end{array}right.$$
Здесь $x_{2}, x_{4}$ – независимые (или свободные)
переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1}, x_{3}, x_{5}$ – зависимые (связанные) переменные
(то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от
пяти переменных) и ранга матрицы $r$ (в этом
случае получили, что $r=3$ – количество
ненулевых строк после приведения матрицы к ступенчатому виду):
$n-r=5-3=2$
Так как ранг матрицы $r=3$ , а количество неизвестных
системы $n=5$ , то тогда количество решений в ФСР
$n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть
для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки).
В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{5}=3 x_{4}
end{array}right.$$
Тогда придавая в первом случае, например, независимым переменным значения
$x_{2}=1$ , $x_{4}=0$ получаем, что $left{begin{array}{l}
x_{1}=-1+6 cdot 0=-1 \
x_{3}=1-frac{5}{2} cdot 0=1 \
x_{5}=3 cdot 0=0
end{array}right.$ . Полученные значения записываем в первую
строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что
{x_{1}=12, x_{3}=-5, x_{5}=6} , что и определяет второе решение ФСР.
В итоге получаем следующую таблицу:
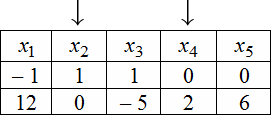
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
$$X_{1}=left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right), X_{2}=left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$
Общее решение является линейной комбинацией частных решений:
$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right)+C_{2}left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$
где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:
$left{begin{array}{l}
x_{1}=-C_{1}+12 C_{2} \
x_{2}=C_{1} \
x_{3}=C_{1}-5 C_{2} \
x_{4}=2 C_{2} \
x_{5}=6 C_{2}
end{array}right.$
$C_{1}, C_{2} neq 0$
Придавая константам $C_{1}, C_{2}$ определенные значения
и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.
Читать дальше: примеры решения СЛАУ.
15.02.2021
Как использовать метод Гаусса?
Сегодня разбираемся с методом Гаусса для решения систем линейных алгебраических уравнений. О том, что это за системы, можно почитать в предыдущей статье, посвященной решению тех же СЛАУ методом Крамера.
Метод Гаусса не требует каких-то специфических знаний, нужна лишь внимательность и последовательность. Несмотря на то что с точки зрения математики для его применения хватит и школьной подготовки, у студентов освоение этого метода часто вызывает сложности. В этой статье попробуем свести их на нет!
Метод Гаусса

Метод Гаусса – наиболее универсальный метод решения СЛАУ (за исключением ну уж очень больших систем). В отличие от рассмотренного ранее метода Крамера, он подходит не только для систем, имеющих единственное решение, но и для систем, у которых решений бесконечное множество. Здесь возможны три варианта.
- Система имеет единственное решение (определитель главной матрицы системы не равен нулю);
- Система имеет бесконечное множество решений;
- Решений нет, система несовместна.
Итак, у нас есть система (пусть у нее будет одно решение), и мы собираемся решать ее методом Гаусса. Как это работает?

Метод Гаусса состоит из двух этапов – прямого и обратного.
Прямой ход метода Гаусса
Сначала запишем расширенную матрицу системы. Для этого в главную матрицу добавляем столбец свободных членов.

Вся суть метода Гаусса заключается в том, чтобы путем элементарных преобразований привести данную матрицу к ступенчатому (или как еще говорят треугольному) виду. В таком виде под (или над) главной диагональю матрицы должны быть одни нули.

Что можно делать:
- Можно переставлять строки матрицы местами;
- Если в матрице есть одинаковые (или пропорциональные) строки, можно удалить их все, кроме одной;
- Можно умножать или делить строку на любое число (кроме нуля);
- Нулевые строки удаляются;
- Можно прибавлять к строке строку, умноженную на число, отличное от нуля.
Обратный ход метода Гаусса
После того как мы преобразуем систему таким образом, одна неизвестная Xn становится известна, и можно в обратном порядке найти все оставшиеся неизвестные, подставляя уже известные иксы в уравнения системы, вплоть до первого.
Когда интернет всегда под рукой, можно решить систему уравнений методом Гаусса онлайн. Достаточно лишь вбить в онлайн-калькулятор коэффициенты. Но согласитесь, гораздо приятнее осознавать, что пример решен не компьютерной программой, а Вашим собственным мозгом.
Пример решения системы уравнений методом Гаусс
А теперь — пример, чтобы все стало наглядно и понятно. Пусть дана система линейных уравнений, и нужно решить ее методом Гаусса:

Сначала запишем расширенную матрицу:

Теперь займемся преобразованиями. Помним, что нам нужно добиться треугольного вида матрицы. Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой и получим:

Затем умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

Умножим 1-ую строку на (6). Умножим 2-ую строку на (13). Добавим 2-ую строку к 1-ой:

Вуаля — система приведена к соответствующему виду. Осталось найти неизвестные:

Система в данном примере имеет единственное решение. Решение систем с бесконечным множеством решений мы рассмотрим в отдельной статье.
Возможно, сначала Вы не будете знать, с чего начать преобразования матрицы, но после соответствующей практики набьете руку и будете щелкать СЛАУ методом Гаусса как орешки.
А если Вы вдруг столкнетесь со СЛАУ, которая окажется слишком крепким орешком, обращайтесь к нашим авторам! Заказать недорого реферат вы можете, оставив заявку в Заочнике. Вместе мы решим любую задачу!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Оценка статьи:




 (нет голосов)
(нет голосов)
![]() Загрузка…
Загрузка…
