Факториал одной сотни записывается как 100! Это произведение всех натуральных чисел до ста включительно. Иногда запись факториала имеет такой вид:
100 х 99 х 98 х 97 х … х 4 х 3 х 2 х 1
Для ответа на вопрос задачи вам не обязательно находить результат умножения. От вас ждут, чтобы вы лишь определили число нулей в конце произведения, не зная, каким именно оно будет. Для решения этой задачи потребуется сформулировать несколько правил. Одно из них вы уже знаете. Взгляните на следующее выражение.
387 000 х 12 900 = 5 027 131 727
Вам не кажется, что здесь есть что-то забавное? Ведь при перемножении двух круглых чисел, то есть тех, которые оканчиваются на нули, невозможно получить некруглое число. Это нарушило бы закон сохранения конечных нулей (закон, который я только что вывел, но, тем не менее, он является верным). Произведение всегда унаследует нулевые окончания своих составляющих. Вот несколько верных примеров этого:
10 х 10 = 100
7 х 20 = 140
30 х 400 = 12 000
Из сомножителей факториала 100 десять заканчиваются на ноль: 10, 20, 30, 40, 50, 60, 70, 80, 90 и 100 (заканчивается на два 0). Это дает уже как минимум одиннадцать конечных нулей, которые 100! обязательно унаследует.
Предупреждение: следование только этому правилу иногда побуждает некоторых кандидатов в своем ответе заявить, что в конце факториала 100 стоят одиннадцать нулей. Такой ответ является неверным. Иногда можно умножить два числа, не заканчивающихся на ноль, и получить произведение, имеющее в конце один или несколько нулей. Вот несколько примеров этого рода:
2 х 5 = 10
5 х 8 = 40
6 х 15 = 90
8 х 125 = 1000
Все, кроме последней пары, входят в сотню составляющих факториала 100. Поэтому ваша работа не закончилась. Теперь мы подходим к закону «сосисок и булочек». Представьте себе ситуацию, когда на пикник одни люди приносят сосиски (в упаковках по десять штук), другие — булочки (упакованные по восемь штук), а некоторые — и то, и другое. Есть единственный способ, позволяющий определить, сколько хотдогов из этих продуктов можно приготовить. Сосчитайте сосиски, сосчитайте булочки и выберите меньшее число из двух.
Тот же самый закон следует использовать и отвечая на наш вопрос. Для этого надо заменить «сосиски» и «булочки» на «сомножители на 2» и «сомножители на 5».
В каждом из приведенных выше уравнений число, которое делится на 2, умножается на число, которое делится на 5. Сомножители на 2 и на 5 при их перемножении «совместно» дают идеальную десятку, что добавляет еще один ноль к общему произведению. Посмотрите на последний пример, где в конце, можно сказать, из воздуха возникает три нуля.
8 х 125 = (2 х 2 х 2) х (5 х 5 х 5)
= (2 х 5) х (2 х 5) х (2 х 5)
= 10 х 10 х 10
= 1000
Поэтому надо составить пары из двоек и пятерок. Возьмем, к примеру, число, равное 692 978 456 718 000 000.
Оно оканчивается на шесть нулей. Это означает, что его можно записать следующим образом:
692 978 456 718 х 10 х 10 х 10 х 10 х 10 х 10,
или так:
692 978 456 718 х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5).
Первая часть, 692 978 456 718, не делится на 10. В ином случае она бы оканчивалась на ноль, и можно было бы эту часть уменьшить еще в 10 раз. К тому же здесь есть шесть сомножителей, равных 10 (или 2 х 5), что соответствует шести нулям в конце числа 692 978 456 718 000 000. Ну как, убедительно?
Это дает нам надежную систему для определения количества нулей в конце любого большого числа. Выделите сомножители 2 и 5. Составьте из них пары и перемножьте их: (2 х 5) х (2 х 5) х (2 х 5) х … Число пар из двоек и пятерок равно количеству нулей в конце. Закройте глаза на все, что осталось слева.
В целом слева у вас останется двойка или пятерка, для которых не нашлось пары. Обычно это двойки. Более того, когда вы имеете дело с факториалом, это всегда двойки. (В факториалах имеется больше четных множителей, чем множителей, которые делятся на 5.) Поэтому узким местом является число пятерок. Из этого следует, что вопрос можно сформулировать по-другому: сколько раз 100! можно разделить без остатка на 5?
Эту арифметическую операцию можно легко проделать даже в голове. В диапазоне от 1 до 100 есть 20 чисел, которые делятся на пятерку: 5, 10, 15, …, 95, 100. Обратите внимание, что 25 дает 2 множителя, равные 5 (25 = 5 х 5), и к тому же в этой группе есть еще три числа, в состав которых входит 25: 50, 75 и 100. В совокупности это добавляет еще четыре пятерки, а всего их 24. 24 множителя на пять дают 24 пары с равным числом двоек, в результате чего получается 24 множителя на 10 (оставляя слева еще множество двоек, для которых не оказалось пары). Таким образом, в конце 100! будет 24 нуля.
Если вам любопытно узнать точный ответ, то значение факториала 100 равно:
93 326 215 443 944 152 681 699 238 856 266 700 490 715 968 264 381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156 518 286 253 697 920 827 223 758 251 185 210 916 864 000 000 000 000 000 000 000 000.
Разбор по книге «Действительно ли Вы достаточно умны, чтобы работать в Google?»
Подсчет конечных нулей факториала числа в любой системе счисления
Время на прочтение
2 мин
Количество просмотров 19K
Как я могу посчитать количество конечных нулей факториала числа в определенной системе счисления?
Давайте рассмотрим случай, когда мы находимся в 10-й системе счисления, а затем посмотрим, как мы можем обобщить это в универсальное решение. Нам дано число N и для его факториала нужно найти количество конечных нулей. Решение будет довольно простым — сумма:
Math.floor(N/5) + Math.floor(N/25) + Math.floor(N/125) + Math.floor(N/625) + ...Её мы можем обобщить в такую формулу:
Почему 5? Это просто. Конечный ноль получается только тогда, когда в составе факториала число имеет 10. Таким образом, посчитав количество десяток в факториале, мы узнаем количество конечных нулей.
Почему в примере выше мы делим на 5? Потому что 10 может быть получено умножением 5 на 2. Поэтому полное решение будет иметь две формулы:
и
Но, рассуждая логически, мы знаем, что первая сумма будет меньше, поэтому нам нужно посчитать только её (подробнее можно почитать тут).
Решение нашей проблемы
Для подсчёта конечных нулей факториала числа в определенной системе счисления я составил алгоритм, приведенный ниже:
- Разложить число B системы счисления на простые множители.
- Разделить число N на каждый уникальной простой множитель K, домножая K сам на себя до тех пор, пока
будет больше единицы, при этом округляя каждый результат до меньшего целого.
- Если при разложении числа системы счисления мы получили несколько одинаковых простых множителей K, то результат выше мы должны разделить на количество одинаковых K.
- Из всех делений N на каждый уникальный множитель K выбрать наименьшее частное, которое и будет нашим ответом.
Я покажу это на примере.
Пусть число N = 5, система счисления B = 12. Факториал 5! = 120, а 120 в 12-ой системе — A0. Мы видим, что в конечной системе счисления факториал исходного числа имеет один ноль. При разложении 12 на простые множители получим 2, 2, 3. У нас есть два уникальных числа: 2 и 3. Следуя нашему алгоритму выполним пункт 2 с числом 2.
Но двойка встречалась дважды при разложении 12-и, поэтому конечный результат мы делим на 2 и округляем до меньшего целого. В результате получаем 1.
Проделываем тоже самое с 3:
Таким образом, мы получили два частных от делений числа N на простые множители числа системы счисления. Они оба равны 1, поэтому меньшее нам выбирать не приходится и мы просто даем ответ — 1.
Рассмотрим еще один пример.
Пусть число N = 16, система счисления B = 16. Факториал 16! = 20922789888000, а 20922789888000 в 16-ой системе — 130777758000. Мы видим, что в конечной системе счисления факториал исходного числа имеет три ноля. При разложении 16 на простые множители, получим 2, 2, 2, 2. Здесь у нас только одно уникальное число, поэтому пункт 2 выполняется только один раз:
При разложении у нас было четыре двойки, поэтому сумму делений делим на 4 с округлением до меньшего целого:
P.S. Большую часть материала для поста перевел отсюда. Автор — Aditya Ramesh.
#статьи
- 19 май 2023
-
0
Что такое факториал и как его вычислить
Статья, после которой вы начнёте щёлкать факториалы как орешки.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Даже если вы уже давно окончили школу, факториалы всё равно могут доставить немало приятных флешбэков — например, если вы обучаетесь программированию и знакомитесь с задачками на рекурсию или комбинаторику. Поэтому мы решили максимально просто объяснить, что такое факториал, как его вычислять и зачем он вообще нужен.
Эта статья будет полезна как опытным программистам, которые хотят освежить знания, так и тем, кто ещё учится: школьникам, студентам и совсем зелёным джунам.
Содержание:
- Что такое факториал
- Для чего он нужен
- Основные свойства и формулы
- Шпаргалка: таблица факториалов
- Решаем задачи на факториалы
- Что запомнить
Факториал числа n — это произведение всех натуральных чисел от единицы до n. Обозначается факториал символом восклицательного знака: !.
Это определение из учебника, и оно пока звучит сложновато — неясно, зачем эти факториалы вообще нужны и как они могут пригодиться в науке и технике. Но об этом чуть позже — для начала давайте посмотрим на примеры факториалов:
Чтобы вычислить их, нам нужно перемножить все числа от единицы до числа, стоящего под знаком факториала — так гласит определение. Получаем выражения:
Ещё в математическом определении сказано, что факториал не может быть отрицательным или дробным — то есть вот такие факториалы вычислить нельзя:
Факториалы незаменимы там, где нужно быстро посчитать количество комбинаций и сочетаний разных предметов. В математике этому посвящён даже целый раздел — комбинаторика. Её методы используют много где: от лингвистики до криптографии и анализа ДНК. И во всех этих сферах факториал помогает упрощать сложные вычисления.
Разберём на примере, как это работает.
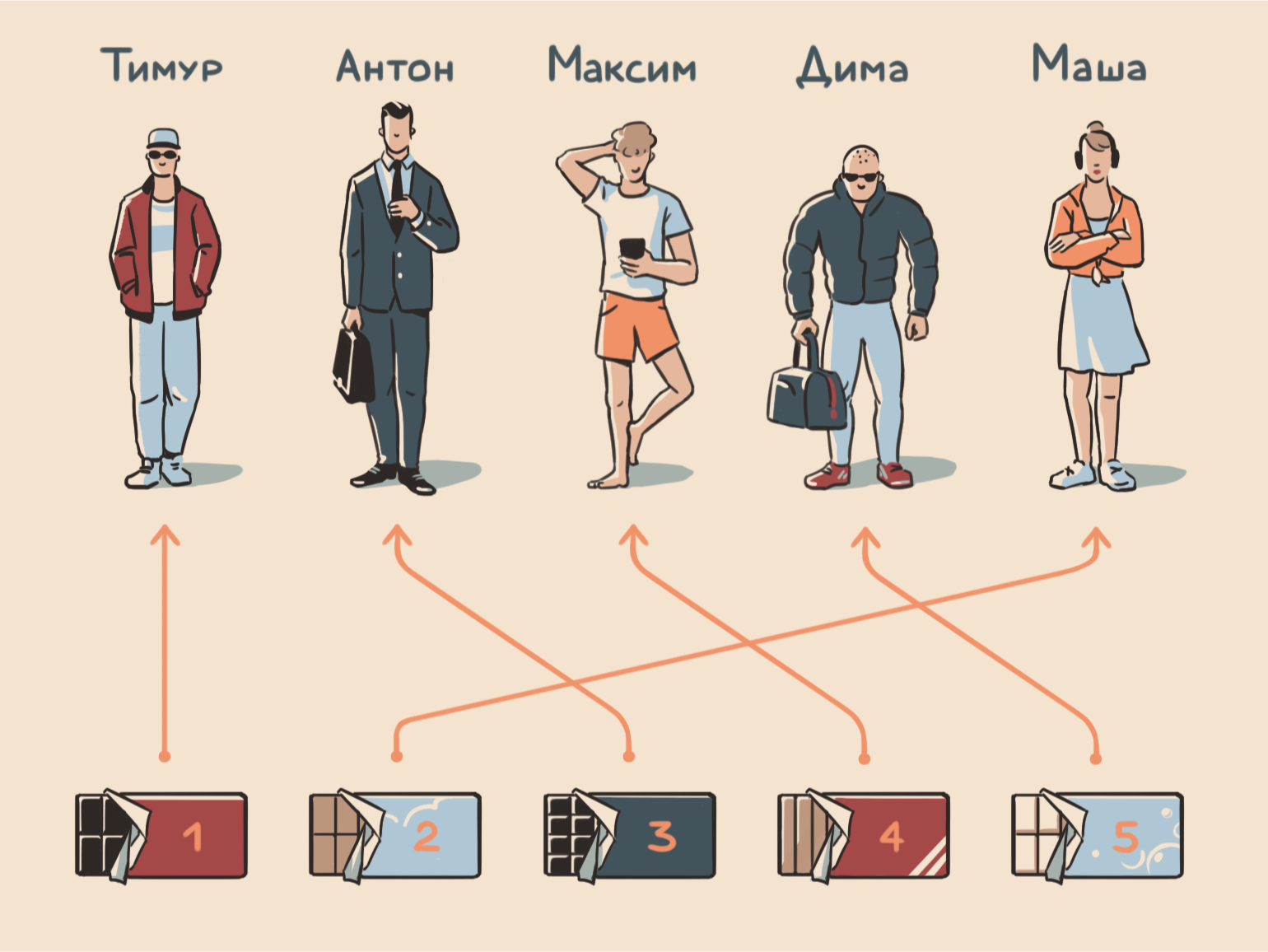
Допустим, у вас есть пять шоколадок и вы решили раздать их пяти друзьям — каждому по одной. Задача — выяснить, сколько существует способов раздать эти шоколадки. Начинаем размышлять:
- первую шоколадку можно отдать одному из пяти друзей;
- вторую — одному из четырёх друзей, потому что один уже получил свою шоколадку;
- третью — одному из трёх, потому что двое уже наслаждаются своими шоколадками;
- четвёртую — одному из двух;
- пятую — последнему другу.
Получается, что способов раздать первую шоколадку — 5, вторую — 4, третью — 3, четвёртую — 2, а пятую — всего 1. По правилам математики, чтобы выяснить общее количество всех вариантов, нужно перемножить их между собой. Ну а кто мы такие, чтобы с этими правилами спорить?
Смотрим на выражение выше и понимаем: ведь оно идеально вписывается в определение факториала — произведение натуральных чисел от одного до n (в нашем случае n равно 5). Следовательно, это выражение можно коротко и изящно записать в виде факториала:
Выходит, что всего способов раздать пять шоколадок пяти друзьям существует 120. Вот как может выглядеть один из них:
Конечно, в жизни вам вряд ли придётся считать количество способов раздать друзьям шоколадки. Но, например, в статистике, теории вероятностей, матанализе и программировании факториалы используют сплошь и рядом. Так что, если видите себя в будущем на матмехе или, на худой конец, в IT, то лучше познакомиться с ними хотя бы бегло.
Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:
- Факториал нуля равен единице — 0! = 1.
- Факториал единицы тоже равен единице: 1! = 1.
- Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.
Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.
Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:
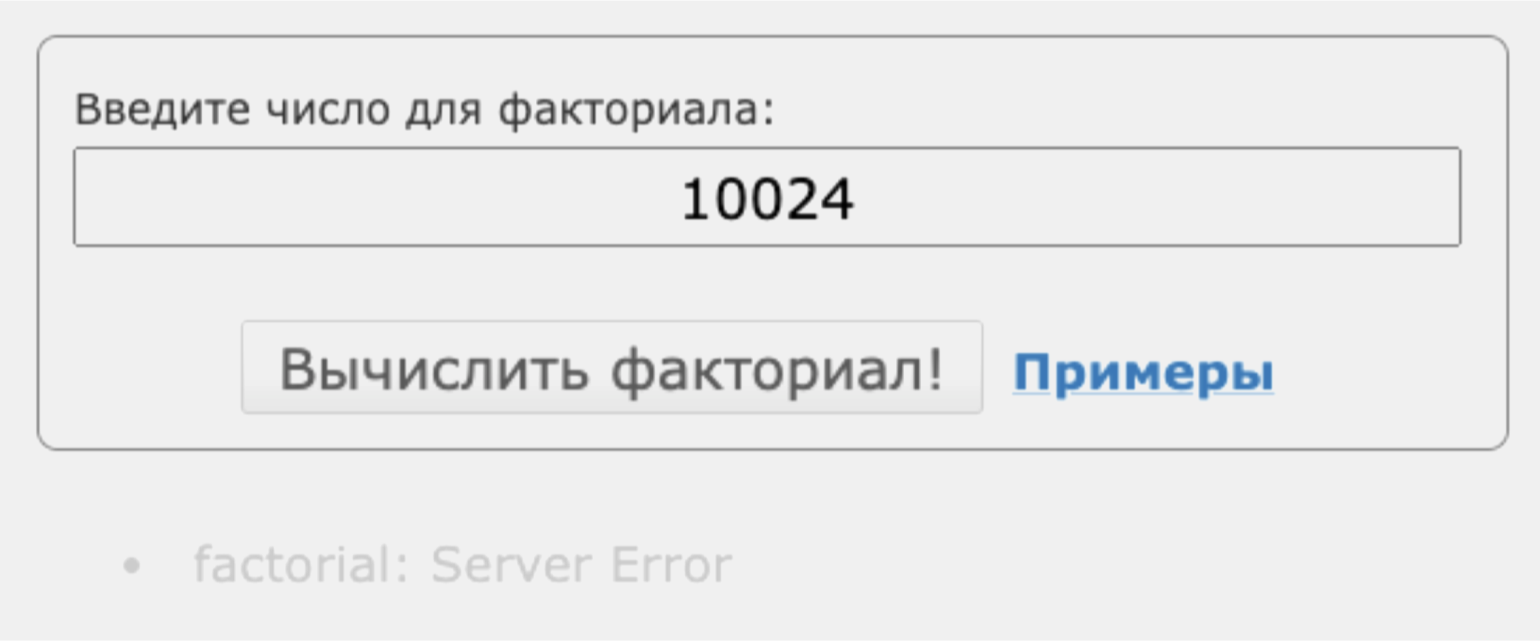
Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).
Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media
Давайте попробуем вычислить факториал числа 6 по этой формуле:
Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:
Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:
Это уже больше похоже на правду. Хотя погрешность всё равно есть.
Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:
В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.
Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.
Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:
Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.
Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:
Можно записать это и в сокращённом виде:
Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:
Получили ответ — 24. Ничего сложного, просто перемножаем числа.
Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:
def factorial(n): # Определяем функцию if n == 0 or n == 1: # Базовый случай return 1 else: # Рекуррентный случай return factorial(n-1) * n # Вызываем эту же функцию, но с меньшим аргументом print(factorial(4)) # Печатаем факториал 4 # Вывод: # 24
Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.
Чтобы быстро находить, чему равен факториал, можно запомнить или сохранить в заметки вот такую табличку. Она рассчитана всего на 12 чисел, но для большинства учебных задач этого хватит.
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
С теорией вроде разобрались — теперь попробуем решить несколько задач с факториалами, чтобы закрепить знания на практике.
Задача: перемножить два факториала.
Решение:
Сперва нужно вычислить значения факториалов, а затем перемножить полученные значения:
Обратите внимание: во второй строке мы применили рекуррентную формулу, чтобы быстрее вычислить факториал числа 7.
Задача: вычесть из одного факториала другой.
Решение:
Используем тот же подход, что и в предыдущей задаче: сначала вычисляем факториалы, а затем получаем ответ на всё выражение.
Вроде бы ничего сложного, главное — не запутаться в умножении.
Задача: умножить один факториал на другой:
Решение:
Вычисляем факториалы, потом перемножаем их значения:
Во второй строке мы воспользовались таблицей выше и быстро нашли значение факториала от числа 8.
Задача: сократить дробь и вычислить её значение.
Решение:
Здесь мы воспользуемся рекуррентной формулой для вычисления факториала и разложим верхний факториал на множители:
В первой строке мы применили рекуррентную формулу два раза, а во второй — просто сократили одинаковые факториалы в числителе и в знаменателе.
Задача: сократить дробь.
Решение:
Хотя здесь нет конкретных чисел, но принцип решения остаётся таким же: используем рекуррентную формулу и сокращаем одинаковые значения в числителе и знаменателе.
Главное — не запутаться и правильно применить рекуррентную формулу.
- Факториал — это произведение всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 будет равен 1 × 2 × 3 × 4 × 5 = 120.
- Его используют во многих областях науки — например, комбинаторике, теории вероятностей и математическом анализе.
- Помимо стандартной формулы для вычисления факториала можно использовать формулы Стирлинга и рекуррентную формулу.
- Формула Стирлинга нужна для того, чтобы посчитать факториал без большого числа операций умножения.
- Рекуррентная формула позволяет вычислить факториал на основе предыдущего факториала.

Научитесь: Профессия Data Scientist
Узнать больше
Given an integer n, write a function that returns count of trailing zeroes in n!.
Examples :
Input: n = 5 Output: 1 Factorial of 5 is 120 which has one trailing 0. Input: n = 20 Output: 4 Factorial of 20 is 2432902008176640000 which has 4 trailing zeroes. Input: n = 100 Output: 24
We strongly recommend that you click here and practice it, before moving on to the solution.
- Approach:
A simple method is to first calculate factorial of n, then count trailing 0s in the result (We can count trailing 0s by repeatedly dividing the factorial by 10 till the remainder is not 0).
- The above method can cause overflow for slightly bigger numbers as the factorial of a number is a big number (See factorial of 20 given in above examples). The idea is to consider prime factors of a factorial n. A trailing zero is always produced by prime factors 2 and 5. If we can count the number of 5s and 2s, our task is done. Consider the following examples.
n = 5: There is one 5 and 3 2s in prime factors of 5! (2 * 2 * 2 * 3 * 5). So a count of trailing 0s is 1.
n = 11: There are two 5s and eight 2s in prime factors of 11! (2 8 * 34 * 52 * 7). So the count of trailing 0s is 2.
- We can easily observe that the number of 2s in prime factors is always more than or equal to the number of 5s. So if we count 5s in prime factors, we are done. How to count the total number of 5s in prime factors of n!? A simple way is to calculate floor(n/5). For example, 7! has one 5, 10! has two 5s. It is not done yet, there is one more thing to consider. Numbers like 25, 125, etc have more than one 5. For example, if we consider 28! we get one extra 5 and the number of 0s becomes 6. Handling this is simple, first, divide n by 5 and remove all single 5s, then divide by 25 to remove extra 5s, and so on. Following is the summarized formula for counting trailing 0s.
Trailing 0s in n! = Count of 5s in prime factors of n!
= floor(n/5) + floor(n/25) + floor(n/125) + ....
Following is a program based on the above formula:
C++
#include <iostream>
using namespace std;
int findTrailingZeros(int n)
{
if (n < 0)
return -1;
int count = 0;
for (int i = 5; n / i >= 1; i *= 5)
count += n / i;
return count;
}
int main()
{
int n = 100;
cout << "Count of trailing 0s in " << 100 << "! is "
<< findTrailingZeros(n);
return 0;
}
Java
import java.io.*;
class GFG {
static int findTrailingZeros(int n)
{
if (n < 0)
return -1;
int count = 0;
for (int i = 5; n / i >= 1; i *= 5)
count += n / i;
return count;
}
public static void main(String[] args)
{
int n = 100;
System.out.println("Count of trailing 0s in " + n
+ "! is "
+ findTrailingZeros(n));
}
}
Python3
def findTrailingZeros(n):
if(n < 0):
return -1
count = 0
while(n >= 5):
n //= 5
count += n
return count
n = 100
print("Count of trailing 0s " +
"in 100! is", findTrailingZeros(n))
C#
using System;
class GFG
{
static int findTrailingZeros(int n)
{
if(n < 0)
return -1;
int count = 0;
for (int i = 5; n / i >= 1; i *= 5)
count += n / i;
return count;
}
public static void Main ()
{
int n = 100;
Console.WriteLine("Count of trailing 0s in " +
n +"! is "+
findTrailingZeros(n));
}
}
PHP
<?php
function findTrailingZeros( $n)
{
if($n < 0)
return -1;
$count = 0;
for ($i = 5; $n / $i >= 1; $i *= 5)
$count += $n / $i;
return $count;
}
$n = 100;
echo "Count of trailing 0s in " , 100,
"! is " , findTrailingZeros($n);
?>
Javascript
<script>
function findTrailingZeros(n)
{
if(n < 0)
return -1;
let count = 0;
for (let i = 5; Math.floor(n / i) >= 1; i *= 5)
count += Math.floor(n / i);
return count;
}
let n = 100;
document.write("Count of trailing 0s in " + 100
+ "! is " + findTrailingZeros(n));
</script>
Output
Count of trailing 0s in 100! is 24
Time Complexity: O(log5n)
Auxiliary Space: O(1)
Approach 2 :- Counting the number of factors of 10 Another way to count the number of trailing zeroes in the factorial of a number is to count the number of factors of 10 in that number’s factorial. This is because a trailing zero is added to the factorial every time a factor of 10 is encountered.
Start the program by including the required header files and the standard namespace.
Define a function named countTrailingZeroes that takes an integer n as input and returns an integer.
Initialize a variable named count to 0, which will be used to count the number of trailing zeroes.
Create a loop that iterates from 1 to n. This loop will be used to calculate the factorial of n.
Within the loop, initialize a variable named j to the current loop variable i.
Create another loop that continues until j is no longer divisible by 5. This inner loop is used to count the number of 5s in the prime factorization of i.
Within the inner loop, increment the count variable and divide j by 5 until j is no longer divisible by 5.
Return the count variable once the loop completes.
Define the main function, which sets n equal to 100 and outputs the result of countTrailingZeroes(n).
End the program by returning 0 from the main function.
In summary, this program calculates the number of trailing zeroes in the factorial of n by counting the number of factors of 5 in the prime factorization of each number from 1 to n.
C++
#include <bits/stdc++.h>
using namespace std;
int countTrailingZeroes(int n)
{
int count = 0;
for (int i = 1; i <= n; i++) {
int j = i;
while (j % 5 == 0) {
count++;
j /= 5;
}
}
return count;
}
int main()
{
int n = 100;
cout << countTrailingZeroes(n) << endl;
return 0;
}
Java
public class Main {
public static int countTrailingZeroes(int n)
{
int count = 0;
for (int i = 1; i <= n; i++) {
int j = i;
while (j % 5 == 0) {
count++;
j /= 5;
}
}
return count;
}
public static void main(String[] args)
{
int n = 100;
System.out.println(countTrailingZeroes(n));
}
}
Python3
def countTrailingZeroes(n):
count = 0
for i in range(1, n+1):
j = i
while j % 5 == 0:
count += 1
j //= 5
return count
n = 100
print(countTrailingZeroes(n))
C#
using System;
class GFG {
static int countTrailingZeroes(int n)
{
int count = 0;
for (int i = 1; i <= n; i++) {
int j = i;
while (j % 5 == 0) {
count += 1;
j /= 5;
}
}
return count;
}
public static void Main(string[] args)
{
int n = 100;
Console.WriteLine(countTrailingZeroes(n));
}
}
Javascript
function countTrailingZeroes(n) {
let count = 0;
for (let i = 1; i <= n; i++) {
let j = i;
while (j % 5 === 0) {
count++;
j = Math.floor(j / 5);
}
}
return count;
}
let n = 100;
console.log(countTrailingZeroes(n));
Time Complexity: O(log5n)
Auxiliary Space: O(1)
This article is contributed by Rahul Jain. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Last Updated :
18 Apr, 2023
Like Article
Save Article
Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается 


.
Например,
.
Для 
.
| n | n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800[1] |
| 14 | 87178291200[2] |
| 15 | 1307674368000[3] |
| 16 | 20922789888000[4] |
| 17 | 355687428096000[5] |
| 18 | 6402373705728000[6] |
| 19 | 121645100408832000[7] |
| 20 | 2432902008176640000[8] |
| 25 | 15511210043330985984000000[9] |
| 50 | 30 414 093 201 713 378 043 612 608 166 064 768 844 377 641 568 960 512 000 000 000 000[10] |
| 70 | 11 978 571 669 969 891 796 072 783 721 689 098 736 458 938 142 546 425 857 555 362 864 628
009 582 789 845 319 680 000 000 000 000 000[11] |
| 100 | ≈9,332621544⋅10157 |
| 450 | ≈1,733368733⋅101000 |
| 1000 | ≈4,023872601⋅102567 |
| 3249 | ≈6,412337688⋅1010000 |
| 10000 | ≈2,846259681⋅1035659 |
| 25206 | ≈1,205703438⋅10100000 |
| 100000 | ≈2,824229408⋅10456573 |
| 205023 | ≈2,503898932⋅101000004 |
| 1000000 | ≈8,263931688⋅105565708 |
| 10100 | ≈109,956570552⋅10101 |
| 101000 | ≈10101003 |
| 1010 000 | ≈101010 004 |
| 10100 000 | ≈1010100 005 |
| 1010100 | ≈101010100 |
Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе, теории чисел, функциональном анализе и др.
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако степенно-показательная функция 

Свойства[править | править код]
Рекуррентная формула[править | править код]
Факториал может быть задан следующей рекуррентной формулой:
Комбинаторная интерпретация[править | править код]
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов.
Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:
ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA
Комбинаторная интерпретация факториала подтверждает целесообразность соглашения 


при 



Связь с гамма-функцией[править | править код]
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Факториал связан с гамма-функцией от целочисленного аргумента соотношением
.
Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при 
Непосредственным обобщением факториала на множества вещественных и комплексных чисел служит пи-функция 

(интегральное определение).
Пи-функция натурального числа или нуля совпадает с его факториалом: 

Формула Стирлинга[править | править код]
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое[12].
Во многих случаях для приближённого вычисления факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что
- 100! ≈ 9,33×10157;
- 1000! ≈ 4,02×102567;
- 10 000! ≈ 2,85×1035 659.
Разложение на простые множители[править | править код]
Каждое простое число p входит в разложение n! на простые множители в степени определяемой следующей формулой:
Таким образом,
где произведение берётся по всем простым числам. Можно заметить, что для всякого простого p большего n соответствующий множитель в произведении равен 1; следовательно, произведение можно брать лишь по простым p, не превосходящим n.
Связь с производной от степенной функции[править | править код]
Для целого неотрицательного числа n:
Например:
Другие свойства[править | править код]
- Для натурального числа
:
- Для любого
:
не является квадратом целого числа;
- Для любого
:
оканчивается на 0;
- Для любого
:
оканчивается на 00.
- Если
простое число:
делится на
(теорема Вильсона)
История[править | править код]
Факториальные выражения появились ещё в ранних исследованиях по комбинаторике, хотя компактное обозначение 

Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что:
Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер. В письме к Кристиану Гольдбаху Эйлер описал требуемое обобщение[15]:
Развивая эту идею, Эйлер в следующем, 1730 году, ввёл понятие гамма-функции в виде классического интеграла. Эти результаты он опубликовал в журнале Петербургской академии наук в 1729—1730 годах.
Обобщения[править | править код]
Двойной факториал[править | править код]
Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.
- Для чётного n:
- Для нечётного n:
Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.
Осуществив замену 


- для чётного числа:
- для нечётного числа:
По договорённости: 
Двойной факториал, так же, как и обычный факториал, определён только для целых неотрицательных чисел.
Последовательность значений n!! начинается так[16]:
- 1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …
Кратный факториал[править | править код]
m-кратный факториал числа n обозначается 



Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.
Кратный факториал связан с гамма-функцией следующим соотношением[18]:
Также кратный факториал 

Неполный факториал[править | править код]
Убывающий факториал[править | править код]
Убывающим факториалом называется выражение
.
Например:
- n = 7; k = 4,
- (n − k) + 1 = 4,
- nk = 7 • 6 • 5 • 4 = 840.
Убывающий факториал даёт число размещений из n по k.
Возрастающий факториал[править | править код]
Возрастающим факториалом называется выражение
Праймориал или примориал[править | править код]
Праймориал или примориал (англ. primorial) числа n обозначается pn# и определяется как произведение n первых простых чисел. Например,
.
Иногда праймориалом называют число 
Последовательность праймориалов (включая 
- 1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 400, 32 589 158 477 190 046 000, 1 922 760 350 154 212 800 000, …
Фибонориал или фибоначчиал[править | править код]
Произведение нескольких первых чисел Фибоначчи. Записывается n!F.
Например, : 6!F = 
Суперфакториалы[править | править код]
Нейл Слоан и Симон Плуффэ[en] в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен
(поскольку устоявшегося обозначения нет, используется функциональное).
В общем
Последовательность суперфакториалов чисел 
- 1, 1, 2, 12, 288, 34 560, 24 883 200, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 737 000 000 000 000, 265 790 267 296 391 960 000 000 000 000 000 000, 127 313 963 299 399 430 000 000 000 000 000 000 000 000 000, …
Идея была обобщена в 2000 году Генри Боттомли[en], что привело к гиперфакториалам (англ. Hyperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел 
- 1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 800 000 000 000, 3 769 447 945 987 085 600 000 000 000 000 000 000 000 000, 6 916 686 207 999 801 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000, …
Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение (m − 1)-уровневых факториалов чисел от 1 до n, то есть
где 


Субфакториал[править | править код]
Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.
См. также[править | править код]
- Факторион
Примечания[править | править код]
- ↑ Шесть миллиардов двести двадцать семь миллионов двадцать тысяч восемьсот
- ↑ Восемьдесят семь миллиардов сто семьдесят восемь миллионов двести девяносто одна тысяча двести
- ↑ Один триллион триста семь миллиардов шестьсот семьдесят четыре миллиона триста шестьдесят восемь тысяч
- ↑ Двадцать триллионов девятьсот двадцать два миллиарда семьсот восемьдесят девять миллионов восемьсот восемьдесят восемь тысяч
- ↑ Триста пятьдесят пять триллионов шестьсот восемьдесят семь миллиардов четыреста двадцать восемь миллионов девяносто шесть тысяч
- ↑ Шесть квадриллионов четыреста два триллиона триста семьдесят три миллиарда семьсот пять миллионов семьсот двадцать восемь тысяч
- ↑ Сто двадцать один квадриллион шестьсот сорок пять триллионов сто миллиардов четыреста восемь миллионов восемьсот тридцать две тысячи
- ↑ Два квинтиллиона четыреста тридцать два квадриллиона девятьсот два триллиона восемь миллиардов сто семьдесят шесть миллионов шестьсот сорок тысяч
- ↑ Пятнадцать септиллионов пятьсот одиннадцать секстиллионов двести десять квинтиллионов сорок три квадриллиона триста тридцать триллионов девятьсот восемьдесят пять миллиардов девятьсот восемьдесят четыре миллиона
- ↑ Тридцать вигинтиллионов четыреста четырнадцать новемдециллионов девяносто три октодециллиона двести один септдециллион семьсот тринадцать седециллионов триста семьдесят восемь квиндециллионов сорок три кваттуордециллиона шестьсот двенадцать тредециллионов шестьсот восемь додециллионов сто шестьдесят шесть ундециллионов шестьдесят четыре дециллиона семьсот шестьдесят восемь нониллионов восемьсот сорок четыре октиллиона триста семьдесят семь септиллионов шестьсот сорок один секстиллион пятьсот шестьдесят восемь квинтиллионов девятьсот шестьдесят квадриллионов пятьсот двенадцать триллионов
- ↑ Одиннадцать дуотригинтиллионов девятьсот семьдесят восемь антригинтиллионов пятьсот семьдесят один тригинтиллион шестьсот шестьдесят девять новемвигинтиллионов девятьсот шестьдесят девять октовигинтиллионов восемьсот девяносто один септемвигинтиллион семьсот девяносто шесть сексвигинтиллионов семьдесят два квинвигинтиллиона семьсот восемьдесят три кватторвигинтиллиона семьсот двадцать один тревигинтиллион шестьсот восемьдесят девять дуовигинтиллионов девяносто восемь анвигинтиллионов семьсот тридцать шесть вигинтиллионов четыреста пятьдесят восемь новемдециллионов девятьсот тридцать восемь октодециллионов сто сорок два септдециллиона пятьсот сорок шесть седециллионов четыреста двадцать пять квиндециллионов восемьсот пятьдесят семь кваттуордециллионов пятьсот пятьдесят пять тредециллионов триста шестьдесят два додециллиона восемьсот шестьдесят четыре ундециллиона шестьсот двадцать восемь дециллионов девять нониллионов пятьсот восемьдесят два октиллиона семьсот восемьдесят девять септиллионов восемьсот сорок пять секстиллионов триста девятнадцать квинтиллионов шестьсот восемьдесят квадриллионов
- ↑ Коэффициенты этого разложения дают A001163 (числители) и A001164 (знаменатели)
- ↑ Крамп, Кристиан. Дата обращения: 19 сентября 2016. Архивировано 19 сентября 2016 года.
- ↑ Pearson, Karl (1924), Historical note on the origin of the normal curve of errors, Biometrika Т. 16: 402–404 [p. 403], DOI 10.2307/2331714: «Стирлинг лишь показал, что арифметическая константа в формуле Муавра равна
. Я считаю, что это не делает его автором теоремы»
- ↑ Дональд Кнут. Искусство программирования, том I. Основные алгоритмы. — М.: Мир, 1976. — С. 79—81. — 736 с.
- ↑ Последовательность A006882 в OEIS
- ↑ «Энциклопедия для детей» Аванта+. Математика.
- ↑ wolframalpha.com Архивная копия от 1 ноября 2013 на Wayback Machine.
- ↑ Последовательность A002110 в OEIS
- ↑ Последовательность A000178 в OEIS
- ↑ Последовательность A055462 в OEIS


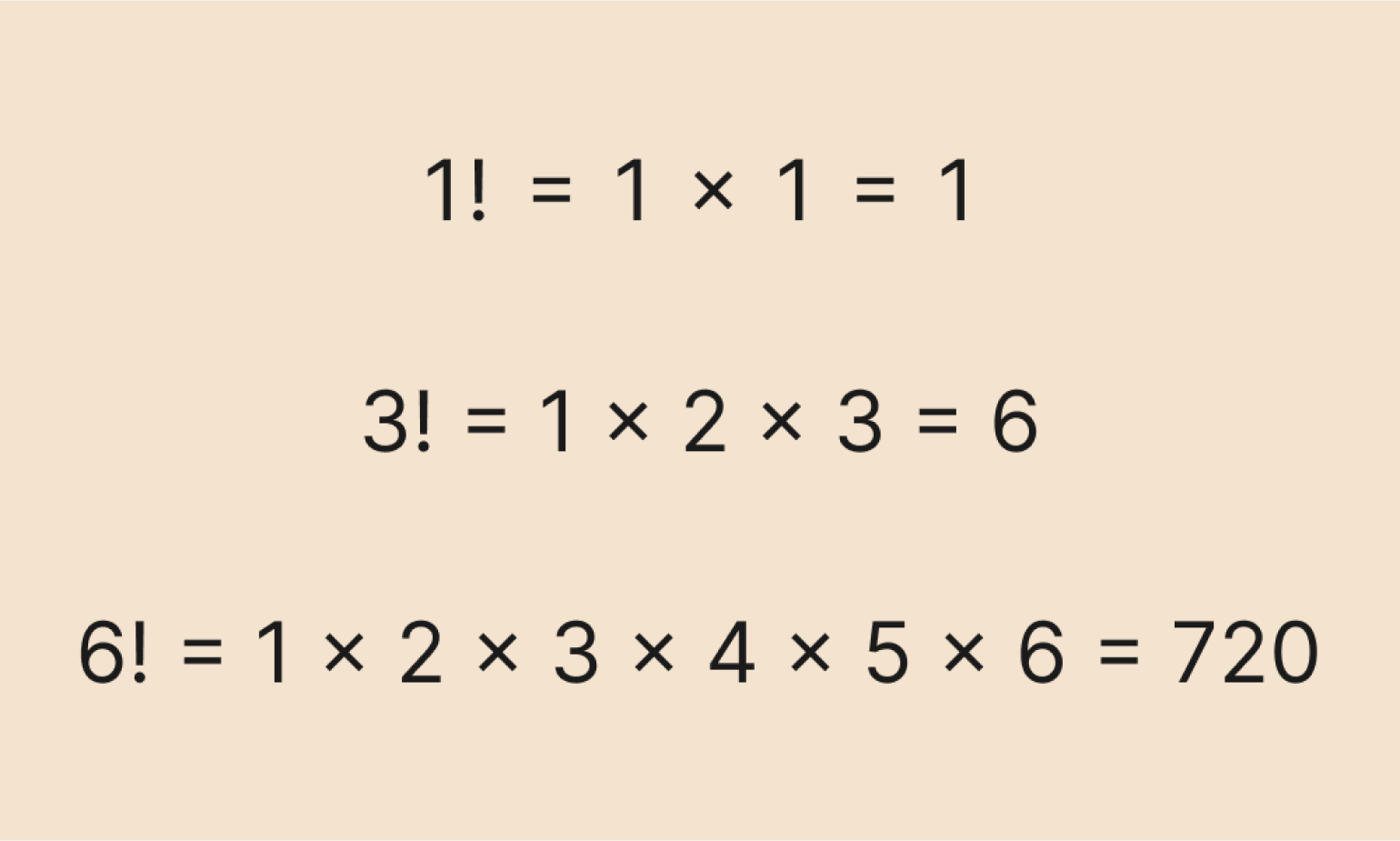

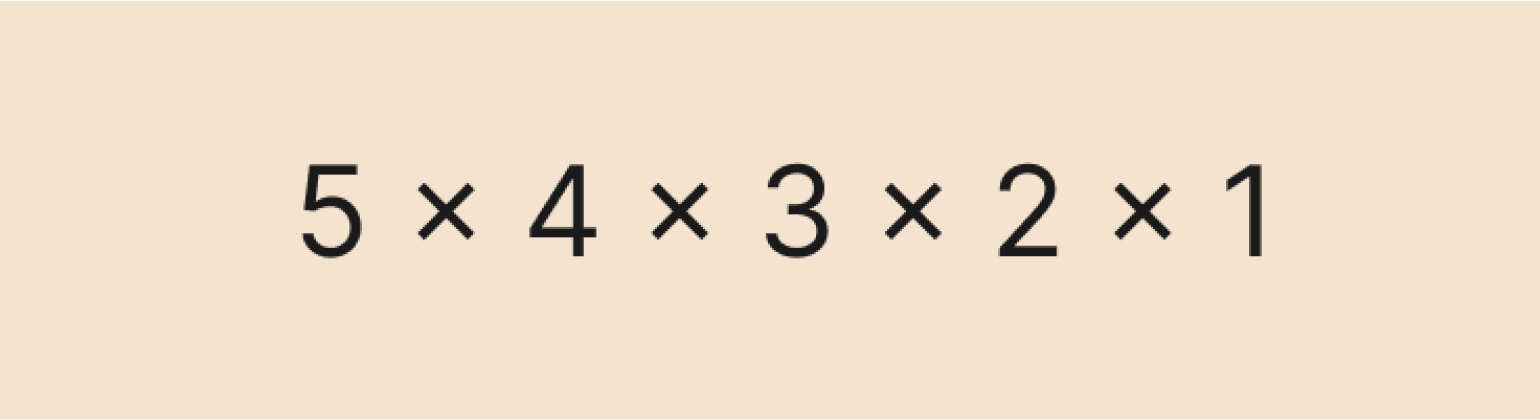
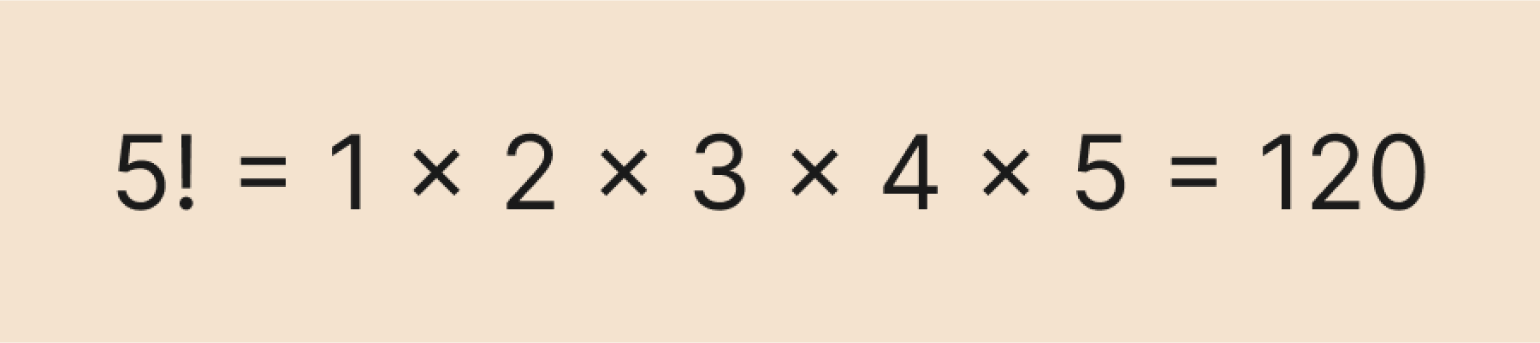
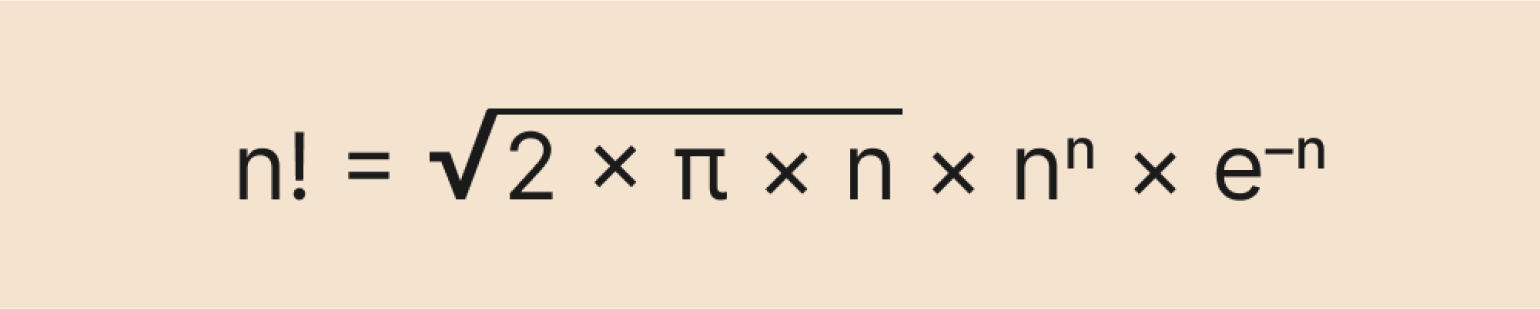
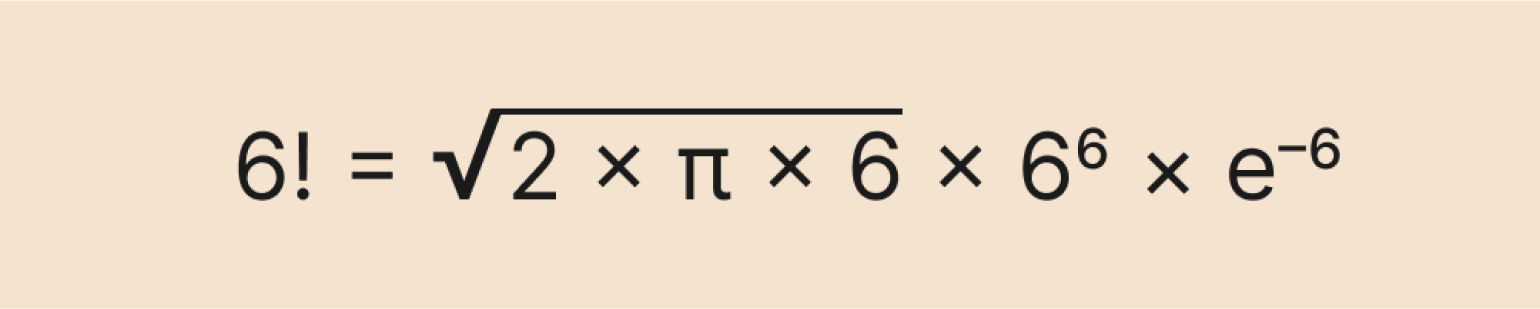
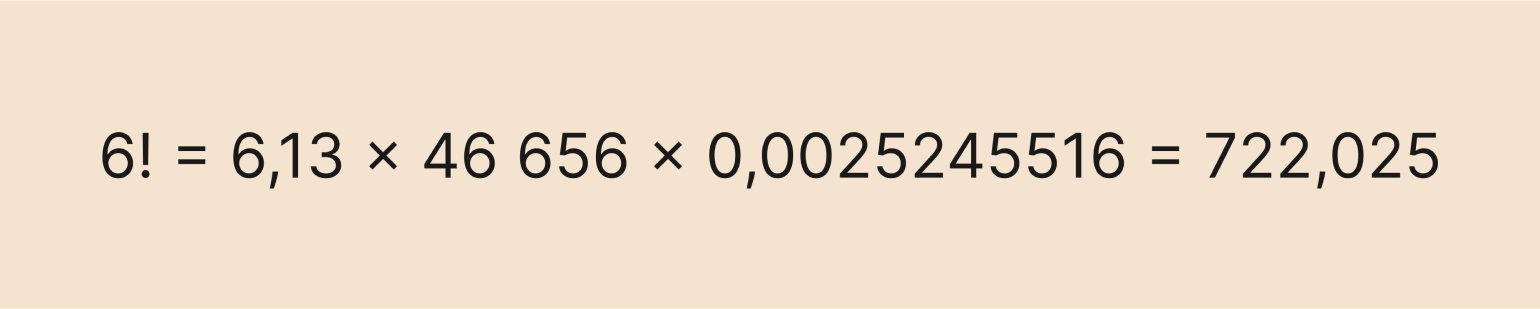

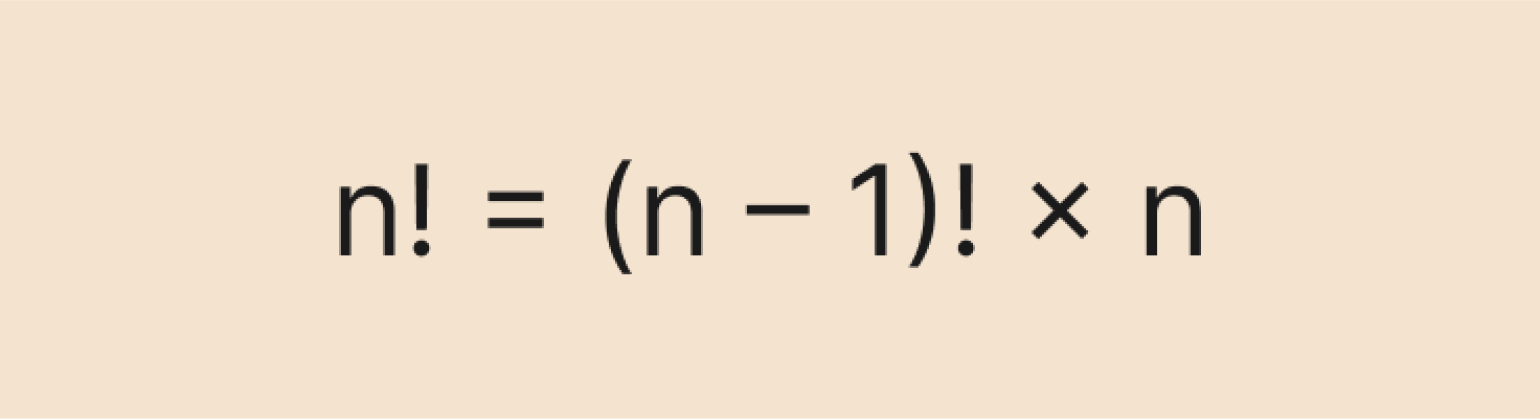

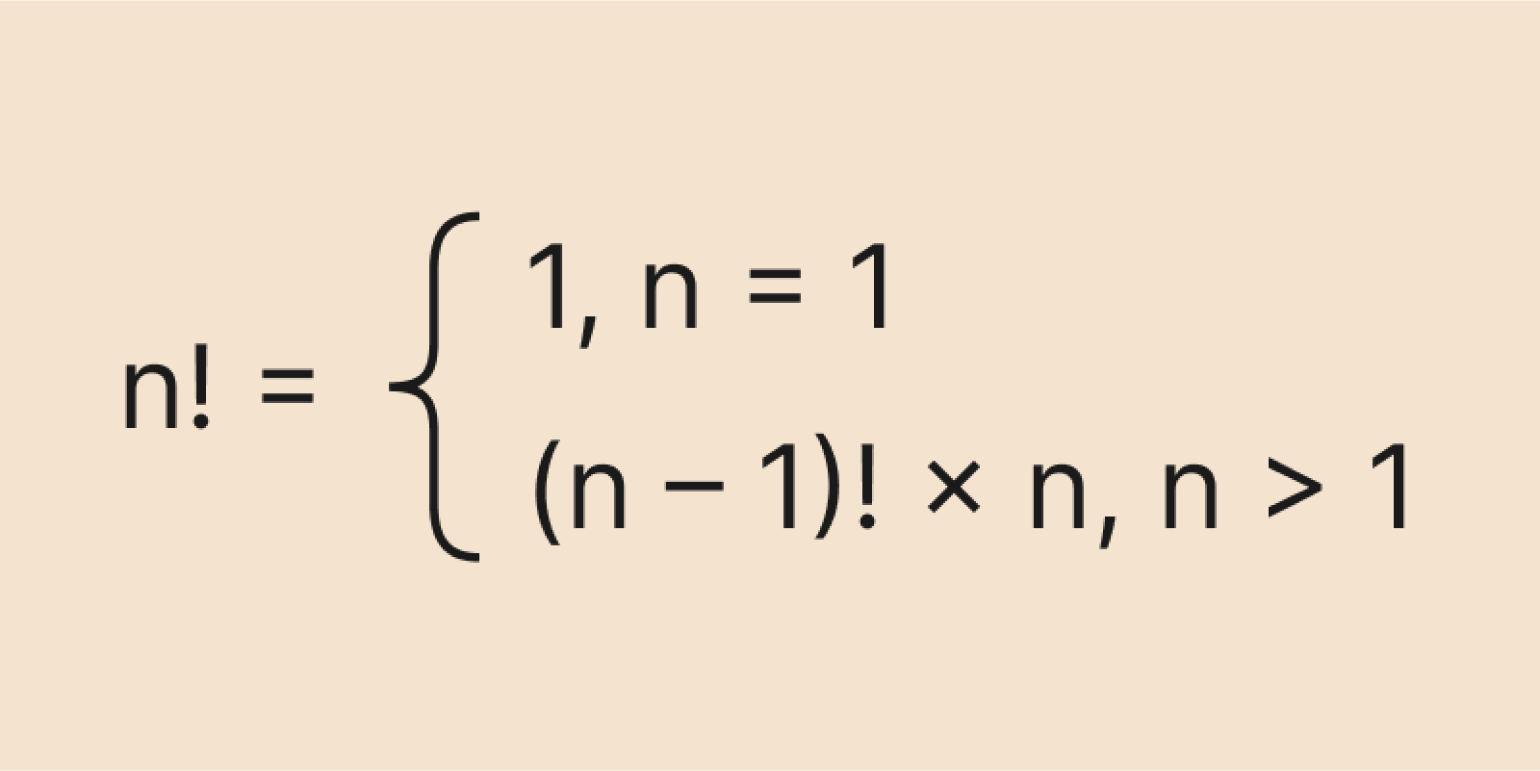
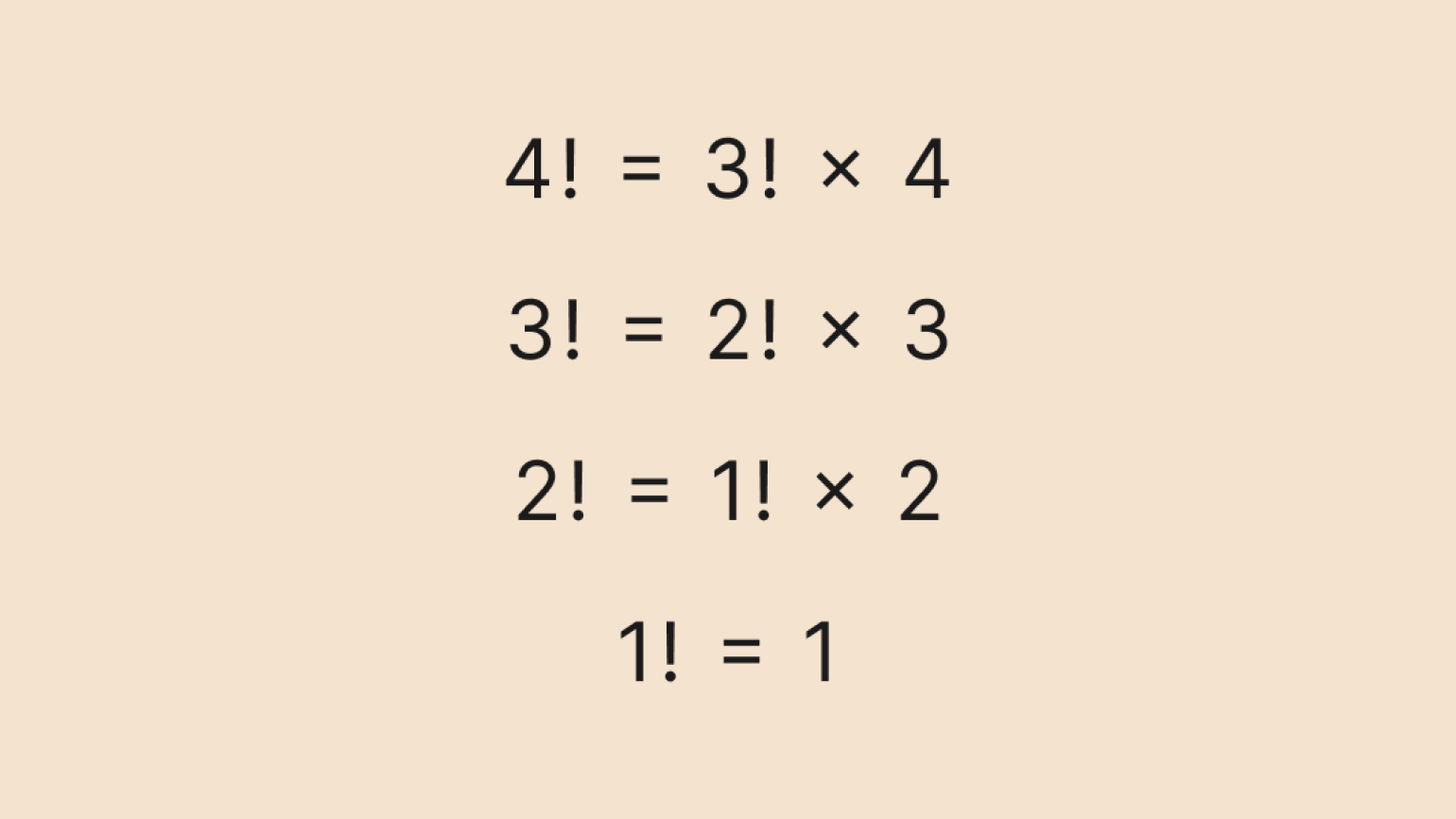
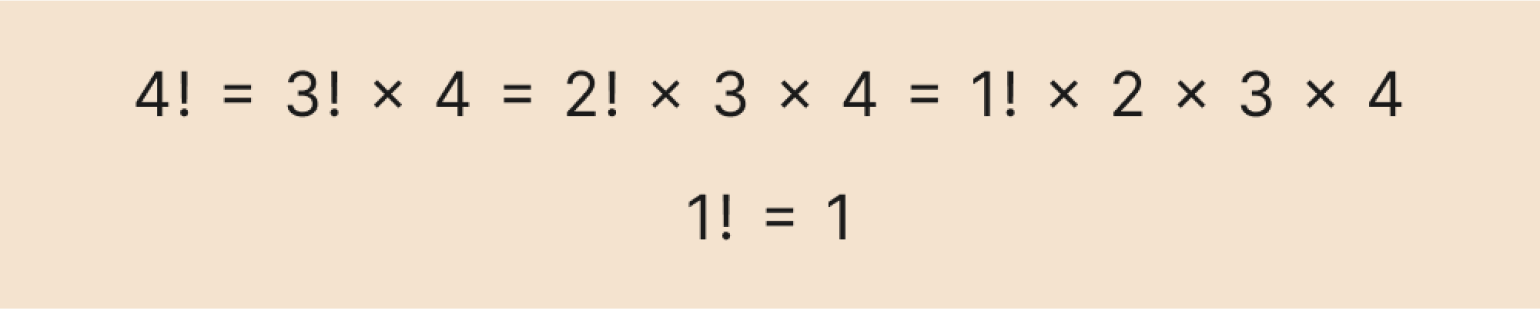
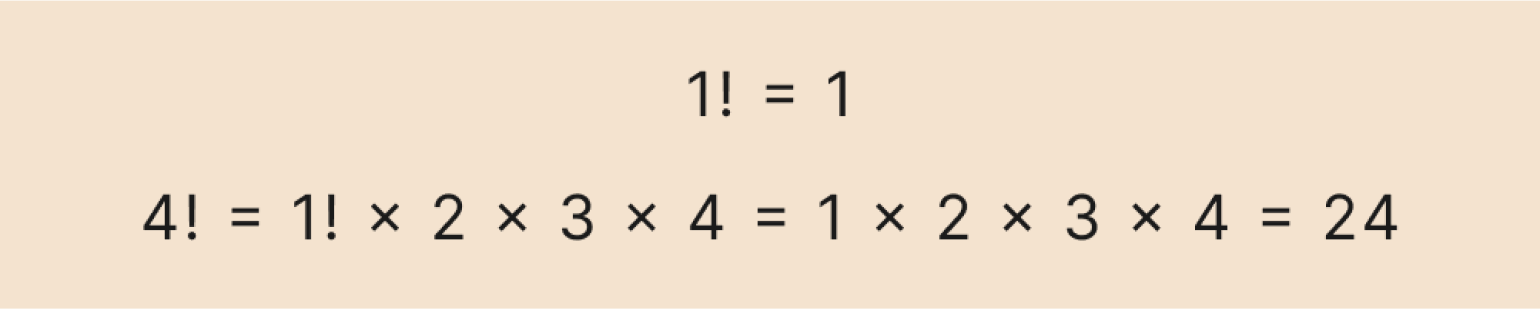


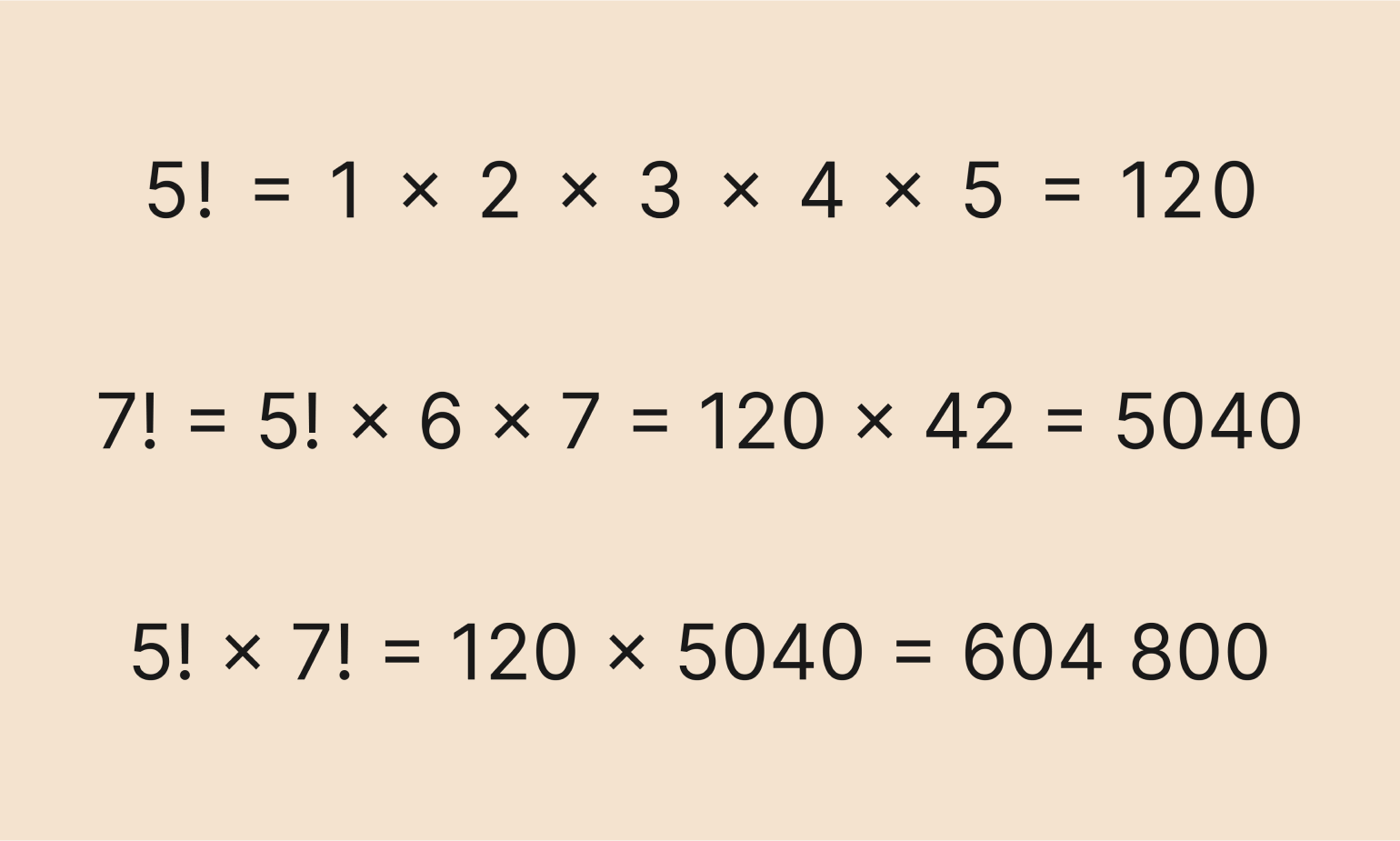

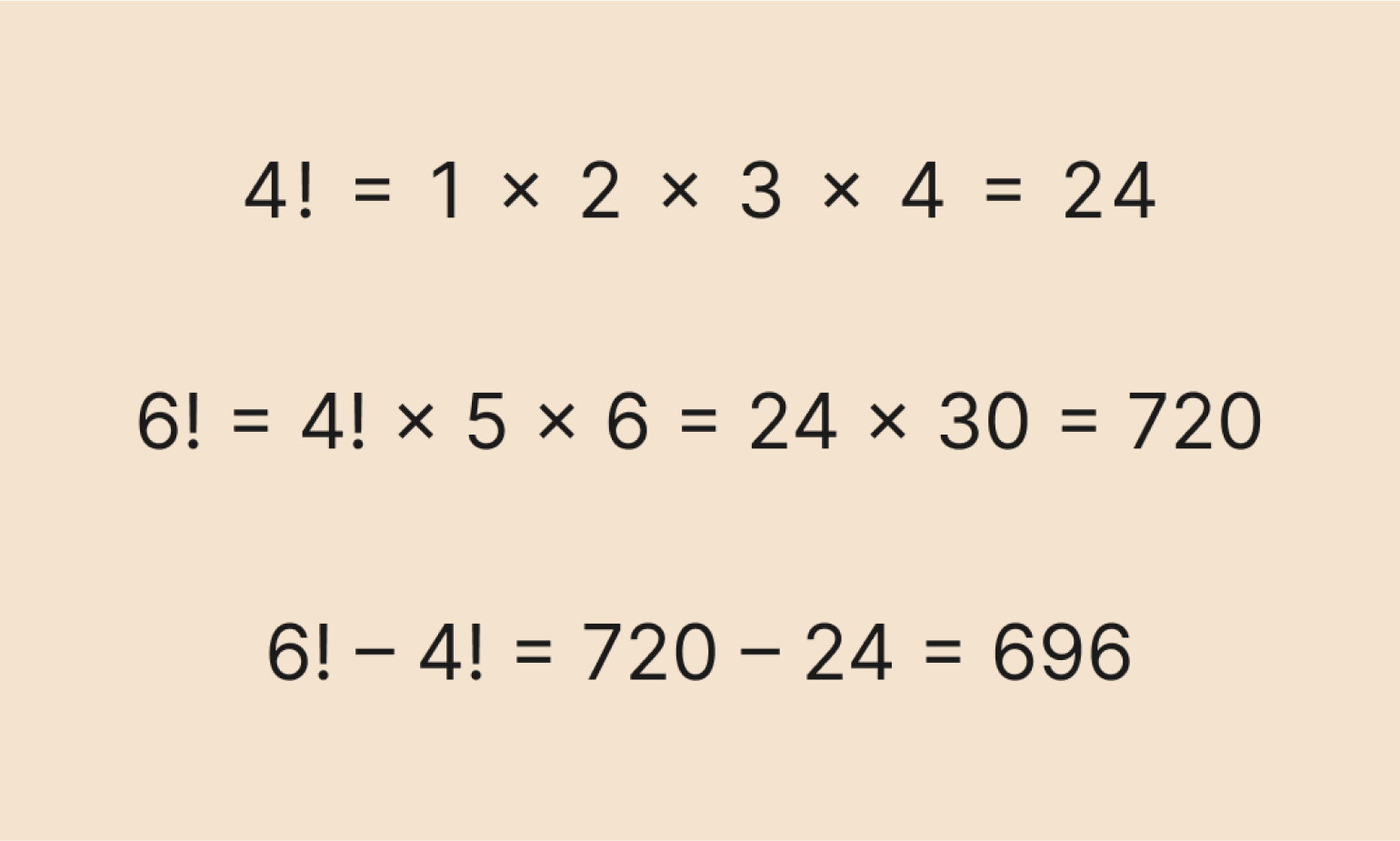

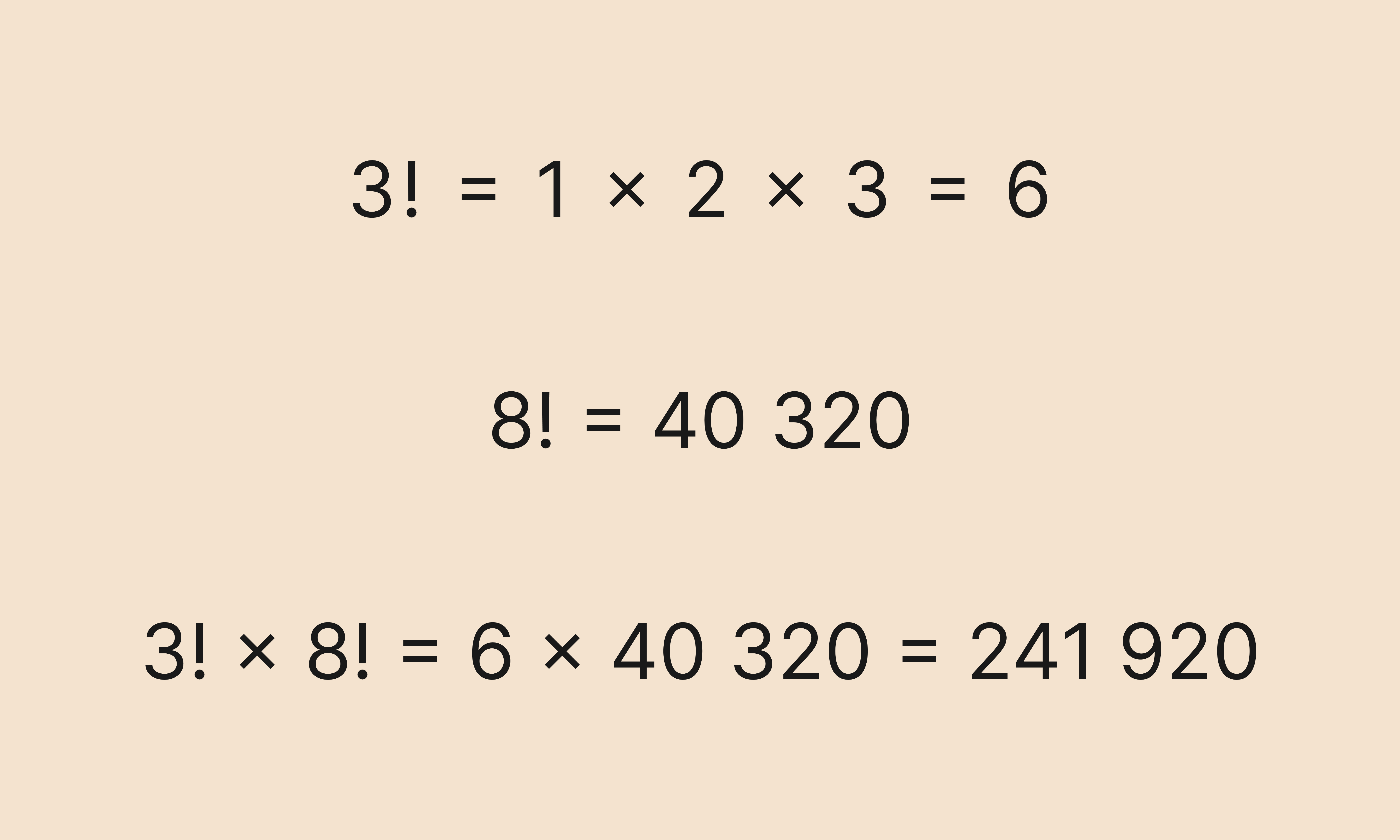

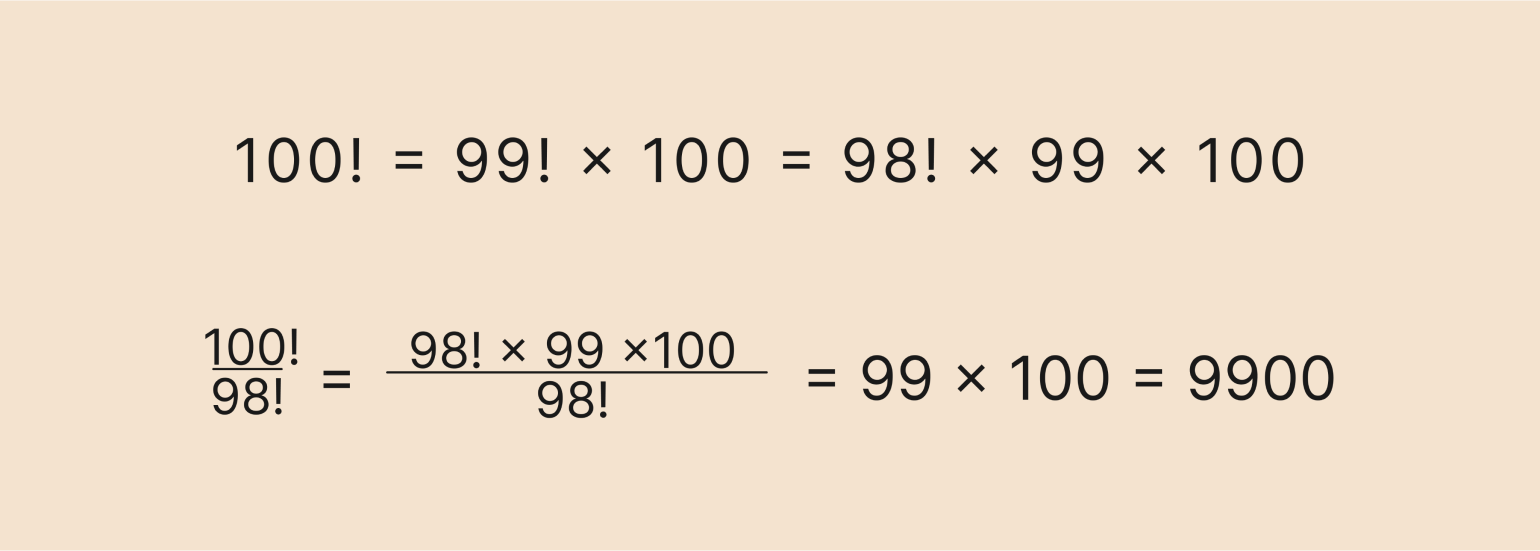
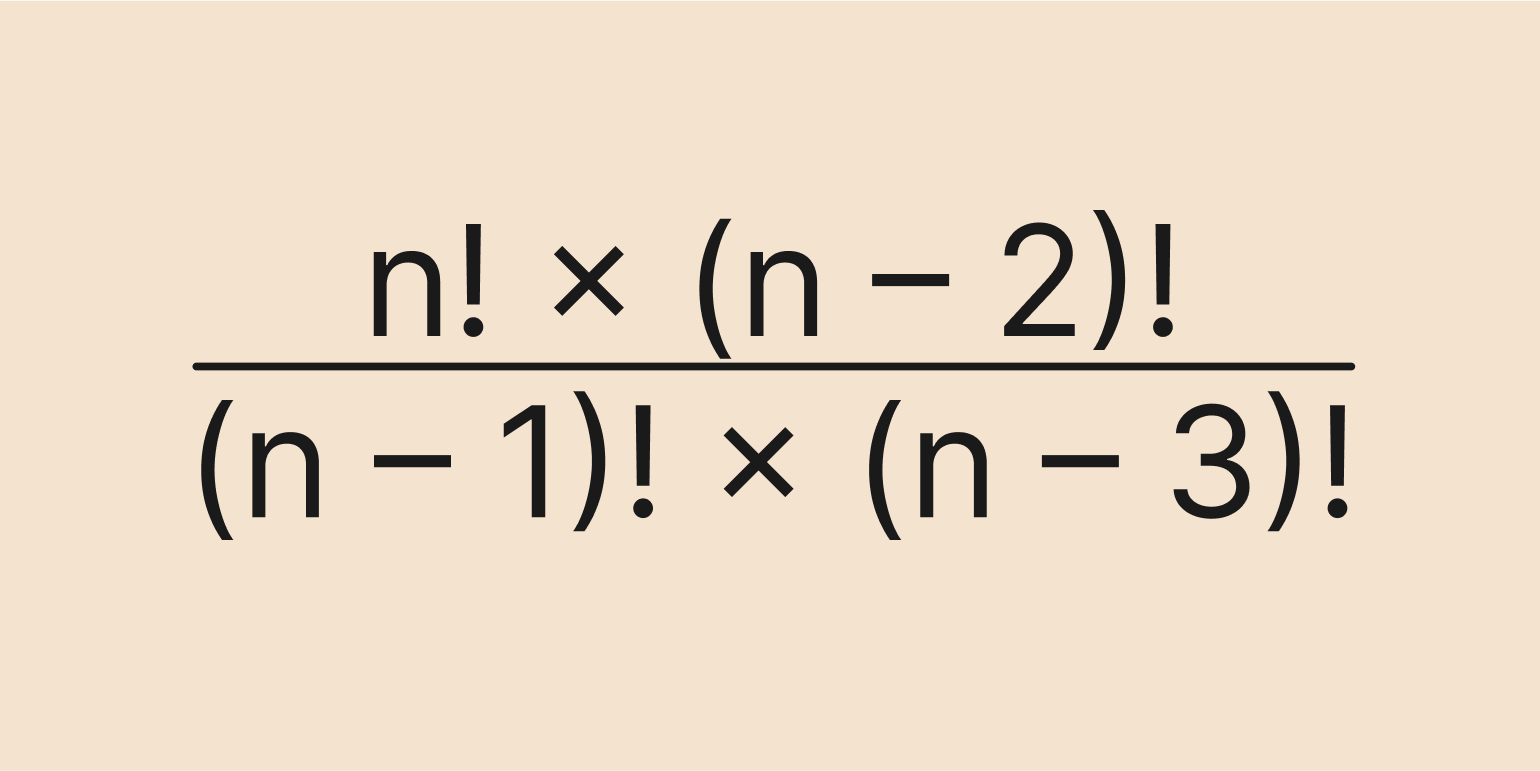
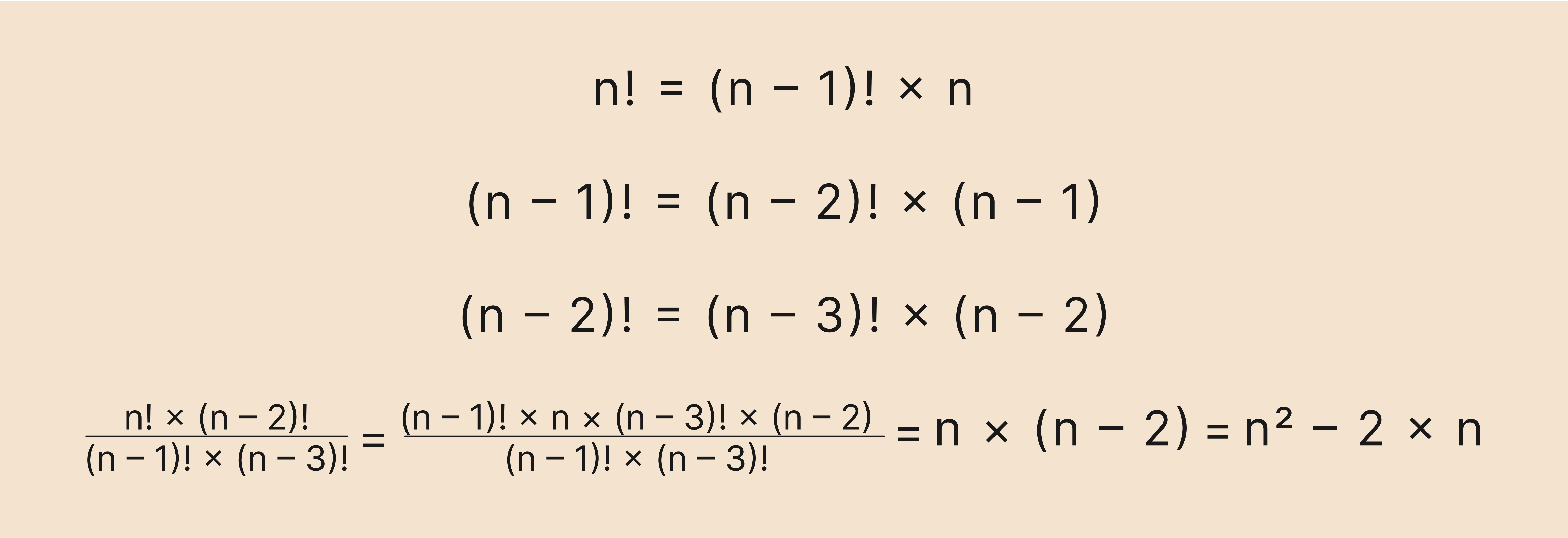





























![(n)_k = n^{underline{k}} = n^{[k]}= ncdot (n-1)cdot ldotscdot (n-k+1) = frac{n!}{(n-k)!} = prod_{i=n-k+1}^n i](https://wikimedia.org/api/rest_v1/media/math/render/svg/001e78ea0bc33bb150e1628f7af1d7d03d5ad1f3)





