Как найти объединение промежутков на координатной прямой

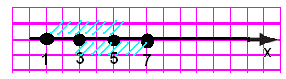
Отметим на координатной прямой точки с координатами –3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше –3 и меньше 2. Верно и обратное: если число х удовлетворяет условию –3 < x < 2.

Множество всех чисел, удовлетворяющих условию –3 < x < 2, называется числовым промежутком или просто промежутком от –3 до 2 и обозначается так: (–3; 2).

На рисунках изображено множество чисел х, для которых выполняется неравенство х < 10 и х ≤ 10. Эти множества представляют собой промежутки, обозначаемые соответственно ((-infty); 10) и ((-infty); 10]. Читается так: число х принадлежит промежутку от минус бесконечности ((-infty)) до 10 (х < 10) и число х принадлежит промежутку от минус бесконечности ((-infty)) до 10, включая число 10 (х ≤ 10). Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают (Acap B).

Промежуток [3; 5] является пересечением промежутков [–1; 5] и [3; 7]. Это можно записать так: [–1; 5] ∩ [3; 7] = [3; 5].

Промежутки [0; 4] и [6; 10] не имеют общих элементов. Если множества не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0; 4] ∩ [6; 10] = 0.

Каждое число из промежутка [1; 7] принадлежит хотя бы одному из промежутков [1; 5] и [3; 7], то есть, либо промежутку [1; 5], либо промежутку [3; 7], либо им обоим.

Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают как (Acup B).

Промежуток [1; 7] является объединением промежутков [1; 5] и [3; 7]. Это можно записать так: ([1;5]cup[3;7]=[1;7].)

Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество ([0;4]cup[6;10]) не является промежутком.

Находя объединение промежутков на координатной прямой: понятно и просто

Объединение промежутков на координатной прямой – это процесс объединения двух или более промежутков на числовой оси. Объединение промежутков – это нахождение максимального промежутка, который содержит все заданные промежутки.

Пример

Допустим, есть два промежутка на числовой оси: $[1,5]$ и $[3,7]$. Сначала нужно найти пересечение этих промежутков, что равно $[3,5]$. Затем, объединение будет равно $[1,7]$.

Алгоритм

1. Сортировка промежутков по начальной точке.
2. Итерации по всем промежуткам. Если начальная точка текущего промежутка находится внутри объединения промежутков (между начальной и конечной точкой), то расширяем объединение до конечной точки текущего промежутка. В противном случае, добавляем текущий промежуток в объединение.
3. Возвращаем объединение.

Реализация на Python

def merge_intervals(intervals):
    intervals.sort(key=lambda x: x[0])
    merged = []
    for interval in intervals:
        if not merged or merged[-1][1] < interval[0]:
            merged.append(interval)
        else:
            merged[-1][1] = max(merged[-1][1], interval[1])
    return merged

Заключение

Объединять промежутки на координатной прямой – это важный инструмент при работе с числовыми данными. Простой алгоритм даёт возможность легко и быстро находить объединение промежутков.

School
at Kazakh-American University

Hand-outs

1.     
КРАТКОЕ СОДЕРЖАНИЕ УРОКА.

Отметим на координатной прямой точки с
координатами -3 и 2. Если точка расположена между ними, то ей соответствует
число, которое больше -3 и меньше 2. Верно и обратное: если число х
удовлетворяет условию -3<x<2 , то оно изображается точкой, лежащей между
точками с координатами -3 и 2.

Множество всех чисел, удовлетворяющих
условию -3<x<2, называется числовым промежутком или
просто промежутком от -3 до 2 и обозначается так: (-3;2).

На рисунках изображены множество чисел х, для которых выполняется неравенство
х<10 и х≤10. Эти множества представляют собой промежутки, обозначаемые
соответственно (-∞; 10) и (-∞; 10]. Читается так: число х принадлежит
промежутку от минус бесконечности (-∞) до 10 (х<10) и число х принадлежит
промежутку от минус бесконечности (-∞) до 10, включая число 10 (х≤10). Знак
равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

Множество, составляющее общую часть
некоторых множеств А и В, называют пересечением этих множеств
и обозначают А∩В. Промежуток [3;5] является
пересечением промежутков [-1;5] и [3;7]. Это можно записать так:
[-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих
элементов. Если множество не имеет общих элементов, то говорят, что их
пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.

Объединение числовых промежутков

Каждое число из промежутка [1;7]
принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо
промежутку [1;5], либо промежутку [3;7], либо им обоим. 

Множество, состоящее из элементов,
принадлежащих хотя бы одному из множеств А и В, называют объединением этих
множеств обозначают AB.

Промежуток [1;7] является объединением
промежутков [1;5] и [3;7]. Это можно записать так: 

Заметим, что объединение промежутков не
всегда представляет собой промежуток, например множество не
является  промежутком.

1.      Числовым
промежутком называется множество всех чисел, удовлетворяющих неравенству.

2.      Знак
равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

3.      Множество,
составляющее общую часть некоторых множеств А и В, называют пересечением этих
множеств и обозначают А∩В.

4.      Множество,
состоящее из элементов, принадлежащих хотя бы одному из множеств А и В,
называют объединением этих множеств обозначают .

2.      КОНТРОЛЬНЫЕ
ВОПРОСЫ:

v Найдите
объединение промежутков [-5; 9] и [7; 12]

v Найдите
пересечение отрезков [-3;5] и [-1;9]

v Запишите
двойное неравенство -2 < y ≤ 0 в виде промежутка:

v Количество
целых решений неравенства: 10 < x ≤ 14

v Найдите
разницу наибольшего и наименьшего целых чисел в промежутке [-10;8)

v Числовой
промежуток, удовлетворяющий неравенству: х ≥ -2

3.     
ГЛОССАРИЙ

4.     
Самостоятельная работа студента: Выучить
урок по hand–outs.

1. СРСП:
   
2. Источники: образовательный портал
   для школьников и студентов http://100ballov.kz

Дата _______математика 6кл

Тема: «Объединение и пересечение числовых промежутков»

Цели:

• ввести понятия пересечения и объединения множеств их обозначения, закрепить понятие числового промежутка, изучение операций объединения и пересечения числовых промежутков и изображений их на координатной прямой.

• способствовать развитию: памяти, речи, внимания, логического мышления.

• Развивающая: способствовать умению сравнивать и анализировать

• Воспитыватательная: способствовать умению оценивать собственный полученный результат

Оборудование: Учебник, рабочая тетрадь, интерактивная доска, презентация Power Point

«Объединение и пересечение числовых промежутков»

Методы: словесный, наглядный, практический.

Основные понятия: интервал, отрезок, полуинтервал, луч, открытый луч; пересечение и объединение промежутков.

Тип урока: урок-объяснение нового материала.

Ход урока

«Ум человеческий только тогда понимает обобщение,

когда он сам его сделал или проверил»

Л. Н. Толстой

1. Организационный момент (5мин)

Приветствие учащихся, проверка их готовности к уроку.

Оценка работы класса с помощью листа контроля

-Здравствуйте, садитесь. Сегоднешний урок пройдет в форме групповой работы. Я вижу что вы все раселись по местам согласна правила разработанного в классе

2. Мотивация урока.

Ребята сейчас я с вами хочу провести игру «Пожелание с сюрпризом». Для этого на ваших столах лежат слова. Вам в течений 1 мин необходимо составить пожелания для других групп и зачитать их. Молодцы

Класс разбит на 4 группы. Каждой группе выдается задание собрать пожелание и зачитать его. Где в каждом пожелании первое слово является словом составляющим тему урока.

1группа-«Объединение ваших действий залог хорошего успеха на уроке»

2группа- «И пусть хорошие оценки радуют вас»

3группа- «Пересечение ваших мыслей результат плодотворного труда»

4 группа-«Числовых промежутков знания, необходимы будут всегда»

А сюрпризом будут слова с ваших пожелании выделенные жирным шрифтом.Как вы думаете что это значит? Тема нашего урока

3. Актуализация опорных знаний. Проверка д/з.(10мин)

Математический диктант.

1. Запишите целые числа в промежутке:

а) [ -5; 2 ] Ответ: -5,-4,-3,-2,-1,0,1,2

2. Запишите и обозначьте данные числовые промежутки:

а) отрезок от 1 до 4 Ответ: [1; 4]
3. Запишите и обозначьте данные числовые промежутки:

б) интервал от 1 до 4 Ответ: (1; 4)
4. Запишите и обозначьте данные числовые промежутки:

в) полуинтервал от 1 до 4, включая 4 Ответ: (1; 4]
5. Запишите и обозначьте данные числовые промежутки:

г) луч от -∞до 5 Ответ: (-∞;5)

4.Изучение нового материала «Пересечение и объединение числовых промежутков» (10 мин)

Отметь на одной чиловой прямой два промежутка: [ — 2; 4] и  [ 1; 6 ]

Назовите промежуток который вы заштриховали? [ — 2; 4]    [ 1; 6 ] = [ -2; 8]

Назовите промежуток где штриховка пересеклась? [ — 2; 4] ∩   [ 1; 6 ] = [ 1; 4]

Рис. 2

Вывод:

Объединением двух числовых промежутков называется числовой промежуток, состоящий из чисел, которые принадлежат хотя бы одному из промежутков

Пересечением числовых промежутков называется числовой промежуток, состоящий из чисел, которые принадлежат одновременно каждому из этих числовых промежутков

Два числовых промежутка между собой могут «пересекаться», «объединятся» или их пересечение может быть ∩   «пустым» множеством. Пересечением двух числовых множеств может быть: интервал, полуинтервал, отрезок.

• Два числовых промежутка могут не пересекаться. Тогда пересечением числовых промежутков

Рис. 3

[ -4; 1]  ∩  [ 3;7] =

[ -4; 1]   [ 3;7] =[ -4; 1]   [ 3;7]

5. Физминутка: Показываю промежутки если интревал, то руки прямо в сторону

если отрезок руки вверх, если луч, руки вниз, полуинтервал одну руку в сторону

6. Работа по закреплению материала (15мин)

Группа-1

1.Изобразите на координатной прямой [1; 6] и [3 ; 10] . Найдите пересечение и объединение промежутков.

Ответ: [1; 6] [3 ; 10]= [3 ; 6] [1; 6] [3 ; 10]= [1 ; 10]

2. Используя координатную прямую, найдите пересечение промежутков

(-4; 6] и ( 0; 7), запишите с помощью обозначений. Найдите наибольшее целое число, удовлетворяющее пересечению промежутков.

Ответ: (-4; 6] ( 0; 7)= (0; 6] целое число=6

3. Используя координатную прямую, найдите объединение промежутков

[1; 10) и [ -3; 8), запишите с помощью обозначений.Запишите в виде неравенства промежуток, удовлетворяющий объединению промежутков.

Ответ: [1; 10)= -3

Группа – 2.

1.Изобразите на координатной прямой (-2; 5] и [3 ; 6] Найдите пересечение и объединение промежутков.

Ответ: (-2; 5] [3 ; 6]= [3 ; 5] (-2; 5] [3 ; 6]=(-2 ; 6]

2. Используя координатную прямую, найдите пересечение промежутков

[-7; 4] и [-2; 5), запишите с помощью обозначений. Найдите наименьшее натуральное число, принадлежащее пересечению числовых промежутков.

Ответ: [-7; 4] [-2; 5)= [-2; 4] натуральное число=0

С-3. Используя координатную прямую, найдите объединение промежутков

[-5; 3) и ( -1; 5), запишите с помощью обозначений. Запишите в виде неравенства промежуток, удовлетворяющий объединению промежутков

Ответ: [-5; 3)= -5

Группа – 3.

1.Изобразите на координатной прямой (-1; 7] и (5 ; 8). Найдите пересечение и объединение промежутков.

Ответ: (-1; 7] [5 ; 8]= [5;7] (-1; 7] [5;8]=(-1 ; 8]

2. Используя координатную прямую, найдите пересечение промежутков

[-3; 9] и [ 1; 11], запишите с помощью обозначений. Найдите наибольшее натуральное число, принадлежащее пересечению числовых промежутков

Ответ: [-3; 9] [1; 11] = [1; 9] натуральное число = 9

3. Используя координатную прямую, найдите объединение промежутков

(-4; 3) и ( -1; 5), запишите с помощью обозначений. Запишите в виде неравенства промежуток, удовлетворяющий объединению промежутков

Ответ: (-1; 3)= -4

Группа– 4.

1.Изобразите на координатной прямой (3; 5] и [-2 ; 4]. Найдите пересечение и объединение промежутков.

Ответ: (3; 5] [-2 ; 4]= (3;4] (3; 5] [-2 ; 4]=[-2 ; 5]

2. Используя координатную прямую, найдите пересечение промежутков

[1; 3) и ( -2; 2), запишите с помощью обозначений. Найдите нименьшее натуральное число, принадлежащее пересечению числовых промежутков

Ответ: [1; 3)= наименьшее натуральное число=1

3. Используя координатную прямую, найдите объединение промежутков

[-6; 1] и ( -4; 3), запишите с помощью обозначений. Запишите в виде неравенства промежуток, удовлетворяющий объединению промежутков

Ответ: [-6; 1] (-4; 3)= (-4; 1] -4

8. Закрепление: «Лови ошибку» (3мин)

Группам дается изображение промежутков где необходимо найти ошибку.

Группа-1

1.[-2; 3) (1; 5]= [-2; 5)

2.[-2; 3) (1; 5]= (1; 5)

Группа-2

1.[1; 5] [3; 7]= (3; 5)

2.[1; 5] [3; 7]= [1; 7]

Группа-3

1.[-2; 3] [1; 6]= [1; 3]

2.[-2; 3] [1; 6]= [-2; 6]

Группа-4

1.[-2; 1) (3; 5]=

2.[-2; 1) (3; 5]=[-2; 1) (3; 5]

9. Подведение итогов урока, выставление оценок. Домашнее задание

Рефлексия

«Закончи предложение» 2мин

Какие новые знания вы получили?

Начните свой ответ со слов:

Я узнал…

Я теперь знаю…

Мне было интересно…

1.Изобразите на координатной прямой (1;7) и (4; 9). Найдите пересечение и объединение промежутков.

2. Используя координатную прямую, найдите пересечение промежутков [ -5; 5] и[ -3;7] запишите с помощью обозначений. Найдите наибольшее целое число, удовлетворяющее пересечению промежутков.

3. Используя координатную прямую, найдите объединение промежутков [ -5;0) и (-2;4] запишите с помощью обозначений.Запишите в виде неравенства промежуток, удовлетворяющий объединению промежутков.

1.Изобразите на координатной прямой (1;7) и (4; 9). Найдите пересечение и объединение промежутков.

Ответ: (1;7) (4;9)= (1;9) (1;7) (4;9)= (4;7)

2. Используя координатную прямую, найдите пересечение промежутков [ -5; 5] и[ -3;7] запишите с помощью обозначений. Найдите наибольшее целое число, удовлетворяющее пересечению промежутков.

Ответ: [ -5; 5] [ -3;7] = [ -3;5] целое число=5

3. Используя координатную прямую, найдите объединение промежутков [ -5;0) и (-2;4] запишите с помощью обозначений.Запишите в виде неравенства промежуток, удовлетворяющий объединению промежутков.

Ответ: [-5; 0)= -5

Задание. Изобразите заданные промежутки на координатной прямой. Найдите пересечение и объединение промежутков. Запишите:

а) (1;7) и (4; 9)
б) [ -5; 5] и[ -3;7]
в) [ -5;0) и (-2;4]
г) (-4;1) и [ 5; 6]

Работа по учебнику Т. А. Алдамуратова «Математика 6 класс», «Атамра» 2011. № 991(1, 2), № 992 (1, 2).

V. Рефлексия

Учитель читает эпиграф к уроку и задает вопрос: «Как вы понимаете слова эпиграфа?
Учащиеся и гости высказывают свое мнение.

VI. Итоги урока

Числовые промежутки.	[-3;6] и [-2;7]	(-∞;5] и [3;+∞)	(-5;8] и [0;7)	(-5;7] и [5;+∞)
Пересечение числовых промежутков
Объединение числовых промежутков

Числовые промежутки.	[-5;3] и [-1;5]	(-∞;3] и [5;+∞)	(-4;7] и [0;5)	(-2;5] и [3;+∞)
Пересечение числовых промежутков
Объединение числовых промежутков

§ 5. Числовые промежутки.

Объединение и пересечение числовых промежутков

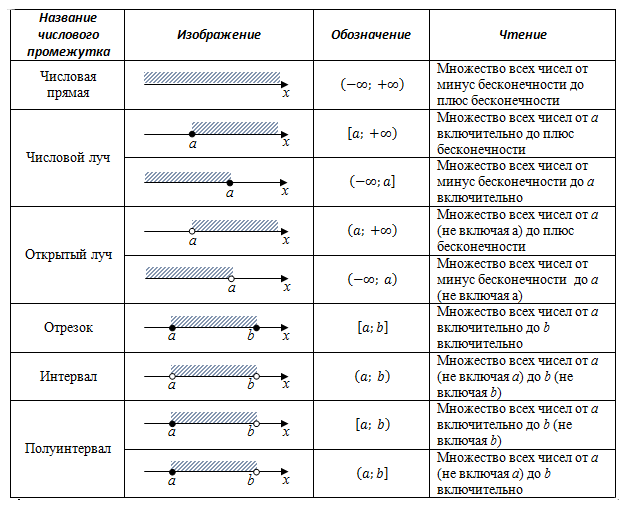
Множество действительных чисел называют также числовой прямой.

В таблице приведены все подмножества множества действительных чисел или части числовой прямой, которые называют числовыми промежутками, а также их характеристики.

Пересечение числовых промежутков

Рассмотрим пересечение множеств, которые являются числовыми промежутками. Например, найдем пересечение отрезка [2; 7] и полуинтервала (5; 9]. Отрезок отметим штриховкой выше координатной прямой, а полуинтервал — ниже. Их пересечение, т. е. общая часть, — это часть прямой с двойной штриховкой (и сверху, и снизу). Так отмечен полуинтервал (5; 7].

Объединение числовых промежутков

Найдем объединение двух числовых промежутков: отрезка [2; 7] и полуинтервала (5; 9], т. е. часть прямой, закрытую двумя этими промежутками. Штриховкой сверху или снизу отмечена часть прямой от 2 до 9. Значит, объединение этих промежутков есть отрезок [2; 9].