Решение некоторых математических задач предполагает нахождение пересечения и объединения числовых множеств. В статье ниже рассмотрим эти действия подробно, в том числе, на конкретных примерах. Полученный навык будет применим для решения неравенств с одной переменной и систем неравенств.
Простейшие случаи
Когда мы говорим о простейших случаях в рассматриваемой теме, то имеем в виду нахождение пересечения и объединения числовых множеств, представляющих из себя набор отдельных чисел. В подобных случаях будет достаточно использования определения пересечения и объединения множеств.
Объединение двух множеств – это множество, в котором каждый элемент является элементом одного из исходных множеств.
Пересечение множеств – это множество, которое состоит из всех общих элементов исходных множеств.
Из указанных определений логически следуют следующие правила:
– чтобы составить объединение двух числовых множеств, имеющих конечное количество элементов, необходимо записать все элементы одного множества и дописать к ним недостающие элементы из второго множества;
– чтобы составить пересечение двух числовых множеств, необходимо элементы первого множества один за другим проверить на принадлежность второму множеству. Те из них, которые окажутся принадлежащими обоим множествам и будут составлять пересечение.
Полученное согласно первому правилу множество будет включать в себя все элементы, принадлежащие хотя бы одному из исходных множеств, т.е. станет объединением этих множеств по определению.
Множество, полученное согласно второму правилу, будет включать в себя все общие элементы исходных множеств, т.е. станет пересечением исходных множеств.
Рассмотрим применение полученных правил на практических примерах.
Исходные данные: числовые множества А = {3, 5, 7, 12} и В = {2, 5, 8, 11, 12, 13}. Необходимо найти объединение и пересечение исходных множеств.
Решение
- Определим объединение исходных множеств. Запишем все элементы, к примеру, множества А: 3, 5, 7, 12. Добавим к ним недостающие элементы множества В: 2, 8, 11 и 13. В конечном итоге имеем числовое множество: {3, 5, 7, 12, 2, 8, 11, 13}. Упорядочим элементы полученного множества и получим искомое объединение: А∪B = {2, 3, 5, 7, 8, 11, 12, 13}.
- Определим пересечение исходных множеств. Согласно правилу, переберем один за другим все элементы первого множества A и проверим, входят ли они во множество B. Рассмотрим первый элемент – число 3: он не принадлежит множеству B, а значит не будет являться элементом искомого пересечения. Проверим второй элемент множества A, т.е. число 5: оно принадлежит множеству B, а значит станет первым элементом искомого пересечения. Третий элемент множества A – число 7. Оно не является элементом множества B, а, следовательно, не является элементом пересечения. Рассмотрим последний элемент множества A: число 1. Оно также принадлежит и множеству B, и соответственно станет одним из элементов пересечения. Таким образом, пересечение исходных множеств – множество, состоящее из двух элементов: 5 и 12, т.е. А∩В = {5, 12}.
Ответ: объединение исходных множеств – А∪B = {2, 3, 5, 7, 8, 11, 12, 13}; пересечение исходных множеств – А∩В = {5, 12}.
Все вышесказанное относится к работе с двумя множествами. Что же касается нахождения пересечения и объединения трех и более множеств, то решение этой задачи возможно свести к последовательному нахождению пересечения и объединения двух множеств. Например, чтобы определить пересечение трех множеств A, В и С, возможно сначала определить пересечение A и B, а затем найти пересечение полученного результата с множеством C. На примере это выглядит так: пусть будут заданы числовые множества: А = {3, 9, 4, 3, 5, 21}, В = {2,7, 9, 21} и С = {7, 9, 1, 3}. Пересечение первых двух множеств составит: А∩В = {9, 21}, а пересечение полученного множества с множеством А∩В = {9, 21}. В итоге: А∩В∩С = {9}.
Однако на практике, чтобы найти объединение и пересечение трех и более простейших числовых множеств, которые состоят из конечного количества отдельных чисел, удобнее применять правила, аналогичные указанным выше.
Т.е., чтобы найти объединение трех и более множеств указанного типа, необходимо к элементам первого множества добавить недостающие элементы второго множества, затем – третьего и т.д. Для пояснения возьмем числовые множества: А = {1, 2}, В = {2, 3}, С = {1, 3, 4, 5}. К элементам первого множества A добавится число 3 из множества B, а затем – недостающие числа 4 и 5 множества C. Таким образом, объединение исходных множеств: А∪В∪С = {1, 2, 3, 4, 5}.
Что же касается решения задачи на нахождение пересечения трех и более числовых множеств, которые состоят из конечного количества отдельных чисел, необходимо одно за другим перебрать числа первого множества и поэтапно проверять, принадлежит ли рассматриваемое число каждому из оставшихся множеств. Для пояснения рассмотрим числовые множества:
А = {3, 1, 7, 12, 5, 2} В = {1, 0, 2, 12} С = {7, 11, 2, 1, 6} D = {1, 7, 15, 8, 2, 6}.
Найдем пересечение исходных множеств. Очевидно, что множество B имеет меньше всего элементов, поэтому именно их мы будем проверять, определяя, входят ли они в остальные множества. Число 1 множества B является элементом и прочих множеств, а значит является первым элементом искомого пересечения. Второе число множества B – число 0 – не является элементом множества A, а, следовательно, не станет элементом пересечения. Продолжаем проверку: число 2 множества B является элементом прочих множеств и становится еще одной частью пересечения. Наконец, последний элемент множества B – число 12 – не является элементом множества D и не является элементом пересечения. Таким образом, получаем: A∩B∩C∩D = {1, 2}.
Координатная прямая и числовые промежутки как объединение их частей
Отметим на координатной прямой произвольную точку, например, с координатой -5,4. Указанная точка разобьет координатную прямую на два числовых промежутка – два открытых луча (-∞, -5,4) и (-5,4, +∞) и собственно точку. Нетрудно увидеть, что в соответствии с определением объединения множеств любое действительное число будет принадлежать объединению (-∞, -5,4)∪ {-5,4} ∪(-5,4, +∞). Т.е. множество всех действительных чисел R = (-∞; +∞) возможно представить в виде полученного выше объединения. И наоборот, полученное объединение будет являться множеством всех действительных чисел.
Отметим, что заданную точку возможно присоединить к любому из открытых лучей, тогда он станет простым числовым лучом (-∞, -5,4] или [-5,4, +∞). При этом множество R будет описываться следующими объединениями: (-∞, -5,4] ∪ (-5,4, +∞) или (-∞, -5,4) ∪ [-5,4, +∞)..
Подобные рассуждения действительны не только относительно точки координатной прямой, но и относительно точки на любом числовом промежутке. Т.е., если мы возьмем любую внутреннюю точку любого произвольного промежутка, его возможно будет представить, как объединение его частей, полученных после деления заданной точкой, и самой точки. К примеру, задан полуинтервал (7, 32] и точка 13, принадлежащая этому числовому промежутку. Тогда заданный полуинтервал можно представить в виде объединения (7, 13) ∪ {13} ∪ (13, 32] и обратно. Мы можем включить число 13 в любой из промежутков и тогда заданное множество (7, 32] можно представить, как (7, 13] ∪ (13, 32] или (7, 13] ∪ (13, 32]. Также мы можем взять в качестве исходных данных не внутреннюю точку заданного полуинтервала, а его конец (точку с координатой 32), тогда заданный полуинтервал можно представить, как объединение интервала (7, 32) и множества из одного элемента {32}. Таким образом: (7, 32] = (7, 32) ∪ {32}.
Еще один вариант: когда берется не одна, а несколько точек на координатной прямой или числовом промежутке. Эти точки разобьют координатную прямую или числовой промежуток на несколько числовых промежутков, а объединение этих промежутков будут составлять исходные множества. К примеру, на координатной прямой заданы точки с координатами -6, 0, 8, которые разобьют ее на промежутки: (-∞, -6), (-6,0), (0, 8), (8, +∞). При этом множество всех действительных чисел, олицетворением чего и является координатная прямая, возможно представить в виде объединения полученных промежутков и указанных чисел:
(-∞, -6) ∪ {-6} ∪(-6,0) ∪ {0} ∪ (0, 8) ∪ {8} ∪ (8, +∞).
Как определить пересечение и объединение при помощи изображений числовых множеств
С темой нахождения пересечения и объединения множеств возможно наглядно разобраться, если использовать изображения заданных множеств на координатной прямой (если только речь – не о простейших случаях, рассмотренных в самом начале статьи).
Мы рассмотрим общий подход, который позволяет определить результат пересечения и объединения двух числовых множеств. Опишем подход в виде алгоритма. Рассматривать его шаги будем постепенно, каждый раз приводя очередной этап решения конкретного примера.
Исходные данные: заданы числовые множества А = (7, +∞) и В = [-3, +∞). Необходимо найти пересечение и объединение данных множеств.
Решение
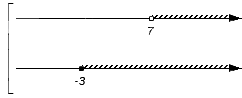
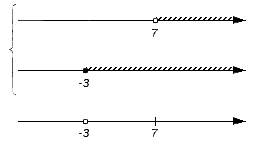
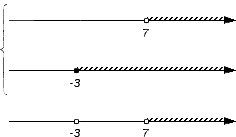
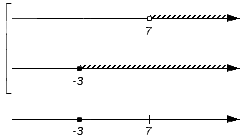
- Изобразим заданные числовые множества на координатных прямых. Их необходимо расположить друг над другом. Для удобства принято считать, что точки начала отсчета заданных множеств совпадают, и остается сохранным расположение точек друг относительно друга: любая точка с большей координатой лежит правее точки с меньшей координатой. При этом, если нам интересно объединение множеств, то координатные прямые объединяют слева квадратной скобкой совокупности; если интересует пересечение, то – фигурной скобкой системы.
В нашем примере для записи пересечения и объединения числовых множеств имеем: 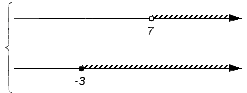
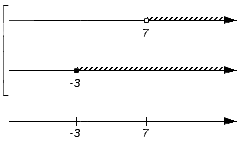
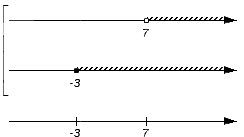
Изобразим еще одну координатную прямую, расположив ее под уже имеющимися. Она понадобится для отображения искомого пересечения или объединения. На этой координатной прямой отмечают все граничные точки исходных числовых множеств: сначала черточками, а позже, после выяснения характера точек с этими координатами, черточки будет заменены выколотыми или невыколотыми точками. В нашем примере это точки с координатами -3 и 7.
Получим:
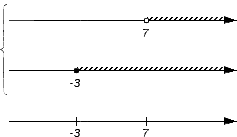
Точки, которые изображены на нижней координатной прямой в предыдущем шаге алгоритма, дают возможность рассматривать координатную прямую как набор числовых промежутков и точек (об этом мы говорили выше). В нашем примере координатную прямую представим в виде набора пяти числовых множеств: (-∞, -3), {-3}, (-3, 7), {7}, (7, +∞).
Теперь необходимо поочередно проверить принадлежность каждого из записанных множеств искомому пересечению или объединению. Получаемые выводы поэтапно отмечаются на нижней координатной прямой: когда промежуток является частью пересечения или объединения, над ним рисуется штриховка. Когда точка входит в пересечение или объединение, то штрих заменяется на сплошную точку; если точка не является частью пересечения или объединения – ее делают выколотой. В этих действиях нужно придерживаться таких правил:
-. промежуток становится частью пересечения, если он одновременно является частью множества A и множества B (или иными словами – если есть штриховка над этим промежутком на обеих координатных прямых, отображающих множества А и B);
– точка становится частью пересечения, если она является одновременно частью каждого из множеств А и В (иными словами – если точка является невыколотой или внутренней точкой какого-либо интервала обоих числовых множеств A и B);
– промежуток становится частью объединения, если он является частью хотя бы одного из множеств A или B (иными словами – если присутствует штриховка над этим промежутком хотя бы на одной из координатных прямых, отображающих множества A и B.
– точка становится частью объединения, если она является частью хотя бы одного из множеств A и B (иными словами – точка является невыколотой или внутренней точкой какого-либо интервала хотя бы одного из множеств A и B).
Кратко резюмируя: пересечением числовых множеств A и B служит пересечение всех числовых промежутков множеств A и B, над которыми одновременно присутствует штриховка, и всех отдельных точек, принадлежащих и множеству А, и множеству В. Объединением числовых множеств A и B служит объединение всех числовых промежутков, над которыми присутствует штриховка хотя бы у одного из множеств A или B, а также всех невыколотых отдельных точек.
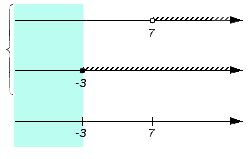
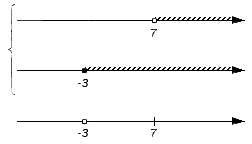
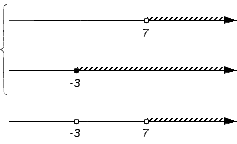
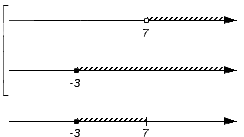
- Вернемся к примеру, определим пересечение заданных множеств. Для этого поочередно проверим множества: (-∞, -3), {-3}, (-3, 7), {7}, (7, +∞). Начнем с множества (-∞, -3), наглядно выделив его на чертеже:
Этот промежуток не будет включен в пересечение, потому что не является частью ни множества A, ни множества B (нет штриховки). И так наш чертеж сохраняет свой изначальный вид:
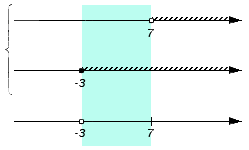
Рассмотрим следующее множество {-3}. Число -3 является частью множества B (невыколотой точкой), но не входит в состав множества A, а потому не станет частью искомого пересечения. Соответственно на нижней координатной прямой точку с координатой -3 делаем выколотой:
Оцениваем следующее множество (-3, 7).
Оно является частью множества B (над интервалом присутствует штриховка), но не входит в множество A (над интервалом штриховка отсутствует): не будет входить в искомое пересечение, а значит на нижней координатной прямой не появляется никаких новых отметок:
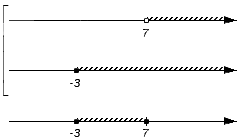
Следующее множество на проверку – {7}. Оно является составом множества B (точка с координатой 7 является внутренней точкой промежутка [-3, +∞) ), но не является частью множества A (выколотая точка), таким образом, рассматриваемый промежуток не станет частью искомого пересечения.. Отметим точку с координатой 7 как выколотую:
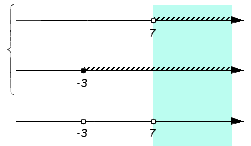
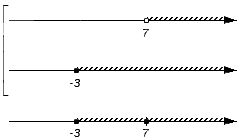
И, наконец, проверяем оставшийся промежуток (7, +∞).
Промежуток входит в оба множества A и B (над промежутком присутствует штриховка), следовательно, становится частью пересечения. Штрихуем место над рассмотренным промежутком:
В конечном счете на нижней координатной прямой образовалось изображение искомого пересечения заданных множеств. Очевидно, что оно является множеством всех действительных чисел больше числа 7, т.е.: А∩В = (7, +∞).
- Следующим шагом определим объединение заданных множеств A и B. Последовательно проверим множества (-∞, -3), {-3}, (-3, 7), {7}, (7, +∞), устанавливая факт включения или невключения их в искомое объединение.
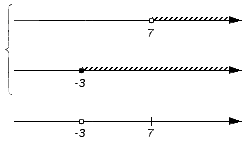
Первое множество (-∞, -3) не является частью ни одного из исходных множеств A и B (над промежутками нет штриховок), следовательно, множество (-∞, -3) не войдет в искомое объединение:
Множество {-3} входит в множество B, а значит будет входить в искомое объединение множеств A и B:
Множество (-3, 7) является составной частью множества B (над интервалом присутствует штриховка) и становится элементом объединения множеств A и B:
Множество 7 входит в числовое множество B, поэтому войдет и в искомое объединение:
Множество (7, +∞), являясь элементом обоих множеств А и В одновременно, становится еще одной частью искомого объединения:
По итоговому изображению объединения исходных множеств А и В получаем: А∩В = [-3, +∞).
Имея некий практический опыт применения правил нахождения пересечений и объединений множеств, описанные проверки легко проводятся устно, что позволяет быстро записывать конечный результат. Продемонстрируем на практическом примере, как выглядит его решение без детальных пояснений.
Исходные данные: множества А =(-∞, -15)∪{-5}∪[0, 7)∪{12} и В =(-20, -10)∪{-5}∪(2, 3)∪{17}. Необходимо определить пересечение и объединение заданных множеств.
Решение
Отметим заданные числовые множества на координатных прямых, чтобы иметь возможность получить иллюстрацию искомых пересечения и объединения:

Ответ: А∩В = (-20,-15)∪{-5}∪(2, 3); А∪В = (-∞, -10)∪{-5}∪[0, 7]∪{12, 17}.
Также понятно, что при достаточном понимании процесса указанный алгоритм возможно подвергнуть оптимизации. К примеру, в процессе нахождения пересечения можно не тратить время на проверку всех промежутков и множеств, представляющих собой отдельные числа, ограничившись рассмотрением только тех промежутков и чисел, которые составляют множество А или В. Прочие промежутки в любом случае не войдут в пересечение, т.к. не являются частью исходных множеств. Составим иллюстрацию сказанного на практическом примере.
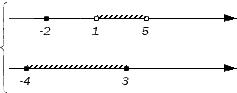
Исходные данные: множества А = {-2}∪[1, 5] и B = [-4, 3].
Необходимо определить пересечение исходных множеств.
Решение
Геометрически изобразим числовые множества А и В:
Граничные точки исходных множеств разобьют числовую прямую на несколько множеств:
(-∞, -4), {-4}, (-4, -2), {-2}, (-2, -1), {1}, (1, 3), {3}, (3, 5), {5}, (5, +∞).
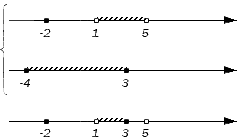
Легко заметить, что числовое множество A можно записать, объединив некоторые из перечисленных множеств, а именно: {-2}, (1, 3), {3} и (3, 5). Достаточно будет проверить эти множества на их включенность также в множество В для того, чтобы найти искомое пересечение. Те, что войдут в множество В и станут элементами пересечения. Проведем проверку.
Совершенно понятно, что {-2} является частью множества B , ведь точка с координатой -2 – внутренняя точка отрезка [-4, 3). Интервал (1, 3) и множество {3} также входят в множество В (над интервалом присутствует штриховка, а точка с координатой 3 является для множества В граничной и невыколотой). Множество (3, 5) не будет элементом пересечения, т.к. не входит в множество В (над ним не присутствует штриховка). Отметим все вышесказанное на чертеже:
В итоге искомым пересечением двух заданных множеств будет объединение множеств, которое мы запишем так: {-2}∪(1, 3].
Ответ: А∩В = {-2}∪(1, 3].
В заключении статьи обговорим еще, как решить задачу о нахождении пересечения и объединения нескольких множеств (более 2). Сведем ее, как рекомендовалось ранее, к необходимости определения пересечения и объединения первых двух множеств, затем полученного результата с третьим множеством и так далее. А можно использовать описанный выше алгоритм с единственным только отличием, что проверку вхождения промежутков и множеств, представляющих собой отдельные числа, необходимо проводить не по двум, а всем заданным множествам. Рассмотрим на примере.
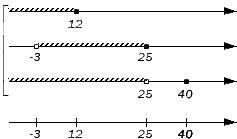
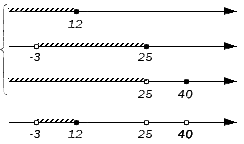
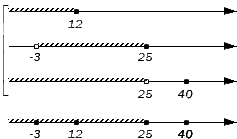
Исходные данные: множества А = (-∞, 12], В = (-3,25], D = (-∞, 25)ꓴ{40}. Необходимо определить пересечение и объединение заданных множеств.
Решение
Отображаем заданные числовые множества на координатных прямых и ставим с левой от них стороны фигурную скобку, обозначая пересечение, а также квадратную, обозначая объединение. Ниже отобразим координатные прямые с отмеченными штрихами граничными точками числовых множеств:
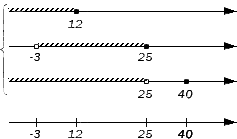
Таким образом, координатная прямая представлена следующими множествами: (-∞, -3), {-3}, (-3, 12), {12}, (12, 25), {25}, (25, 40), {40}, (40, +∞).
Начинаем искать пересечения, поочередно проверяя записанные множества на принадлежность каждому из исходных. Во все три заданных множества входит интервал (-3, 12) и множество {-12}: они и станут элементами искомого пересечения. Таким образом, получим: A∩B∩D = (-3, 12].
Объединение заданных множеств составят множества: (-∞, -3) – элемент множества А; {-3} – элемент множества А; (-3, 12) – элемент множества А; {12} – элемент множества А; (12, 25) – элемент множества В; {25} – элемент множества В и {40} – элемент множества D. Таким образом, получим: A∪B∪D = (-∞, 25] ∪ {40}.
Ответ: A∩B∩D = (-3, 12]; A∪B∪D = (-∞, 25] ∪ {40}.
Отметим также, что искомое пересечение числовых множеств часто является пустым множеством. Происходит это в тех случаях, когда в заданные множества не включены элементы, одновременно принадлежащие им всем.
Исходные данные: А = [-7, 7]; В = {-15}∪[-12, 0)∪{5}; D = [-15, -10]∪[10, +∞); Е = (0, 27). Определить пересечение заданных множеств.
Решение
Отобразим исходные множества на координатных прямых и штрихами граничные точки этих множеств на дополнительной прямой.
Отмеченные точки разобьют числовую прямую на множества: (-∞, -15), {-15}, (-15, -12), {-12}, (-12, -10), {-10}, (-10, -7), {-7}, (-7, 0), {0}, (0, 5), {5}, (5, 7), {7}, (7, 10), {10}, (10, 27), {27}, (27, +∞).
Ни одно из них не является одновременно элементом всех исходных множеств, следовательно, пересечение заданных множеств есть пустое множество.
Ответ: A∩B∩D∩Е = Ø.
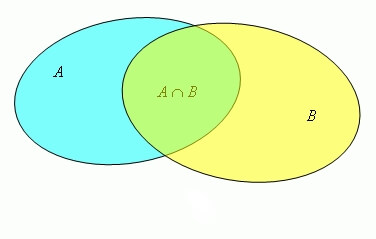
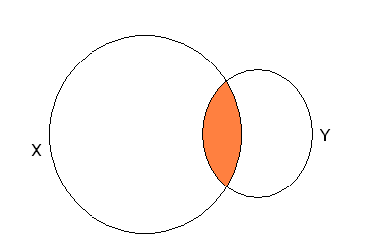
Множества удобно изображать в виде кругов, которые называют кругами Эйлера.
На рисунке множество пересечения множеств X и Y закрашено в оранжевый цвет.
Объединение A и B
Объедине́ние мно́жеств (тж. су́мма или соедине́ние) в теории множеств — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств 




Содержание
- 1 Определения
- 1.1 Объединение двух множеств
- 1.2 Объединение семейства множеств
- 2 Свойства
- 3 Примеры
- 4 Примечания
- 5 См. также
Определения[править | править код]
Объединение двух множеств[править | править код]
Пусть даны два множества 

Объединение семейства множеств[править | править код]
Пусть дано семейство множеств 
Свойства[править | править код]
- Объединение множеств является бинарной операцией на произвольном булеане
- Операция объединения множеств коммутативна:
- Операция объединения множеств ассоциативна:
- Операция объединения множеств дистрибутивна относительно операции пересечения:[1]
- Пустое множество
является нейтральным элементом операции объединения множеств:
- Таким образом булеан вместе с операцией объединения множеств является моноидом;
- Операция объединения множеств идемпотентна:
Примеры[править | править код]
- Пусть
Тогда
Примечания[править | править код]
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 66. — 672 с. — ISBN 5-482-00445-7.
См. также[править | править код]
- Дизъюнктное объединение
- Операции над множествами
Теория множеств |
||
|---|---|---|
| Обзор |
|
|
| Аксиомы |
|
|
| Операции |
|
|
|
|
|
| Типы множеств |
|
|
| Теории |
|
|
|
|
|
| Теоретики множеств |
|
Решение некоторых математических задач предусматривает операции над множествами такие как пересечение, объединение, разность. Под множеством подразумевают объединение некоторых предметов в одно целое. Для совершения подобных действий требуется знание некоторых правил, которые позволят найти пересечение, объединение и разность множеств. О таких правилах пойдёт речь далее.
Обозначение множеств. Как записать объединение и пересечение множеств
Определения
Объединение множеств – это ряд таких элементов, при которым каждый из них представляет собой элемент одного из первоначальных множеств.
Пересечение множеств — заключает в себе все элементы, общие для первоначальных множеств.
При записи обозначения пересечения множеств и объединения множества чисел, используют специальный порядок символов. Самый лёгкий способ обозначить множество — это применение фигурных скобок, в середине которых элементы записаны через запятую.
А = {7, 3, 15, 31}
С помощью такой записи можно задать множество, если оно включает небольшое конечное число элементов. В связи с этим чаще применяется многофункциональный способ определения множеств – посредством характеристического свойства, которое свойственно всем элементам множества, которым не владеют объекты вне множества.
A = {x | P(x)} или A = {x : P(x)}
P(x) – характеристическое свойство множества A.
В таком виде объединение записывается следующим образом:
AUB={x|xєAvxєB}
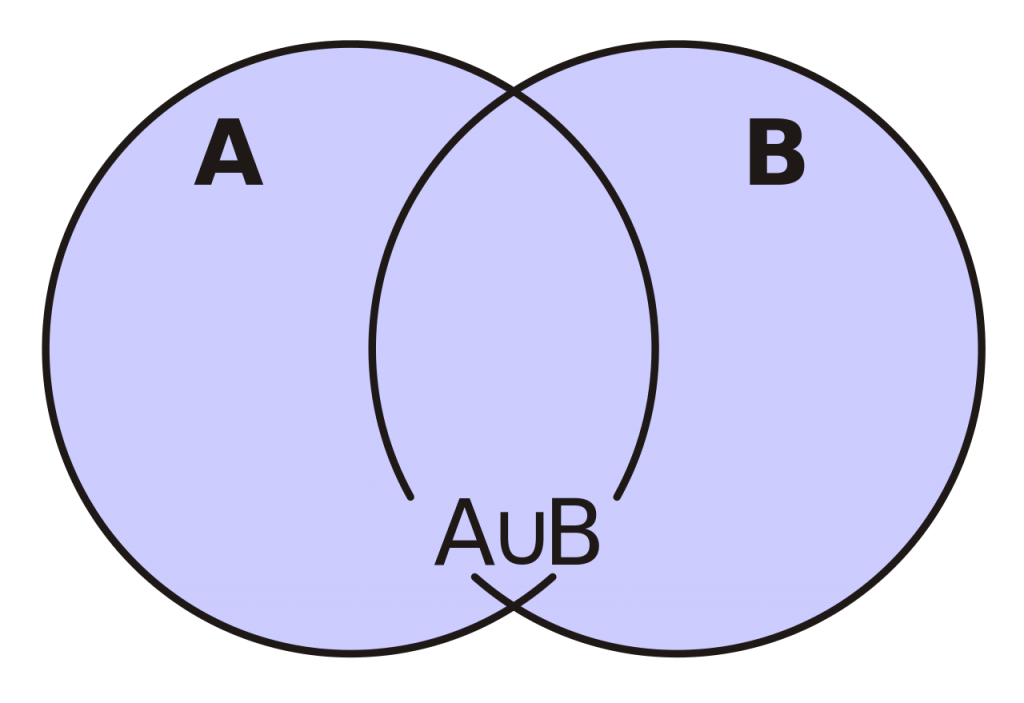
а пересечение множеств записывается как:
AՈB={x|xєAᴧxєB}
Где символы v / ᴧ, обозначают «или» / «и», символ | обозначает «таких что».
Чтобы обозначить множества, как числовые интервалы, при записи применяют скобки круглой и квадратной формы. К примеру, запись [4,24), выражает цифровой диапазон от 4 до 24, при этом число 4 входит в состав множества, а 24 нет. Числа менее 24 принадлежат этому множеству.
Найти пересечение и объединение множеств. Операции над множествами
Важно
U – обозначает объединение множеств A и B;
Ո – обозначает пересечение множеств A и B.
Чтобы легче запомнить данные знаки пересечения и объединения множеств, можно мысленно представить, что символ объединения U напоминает сосуд с открытым верхом, туда есть возможность что-то положить.
Символ пересечения Ո наоборот, выглядит как перевёрнутая ёмкость, в который невозможно поместить какой-либо предмет. Так же символ обозначающий пересечение Ո можно прочитать как «И».
Тогда выражение AՈB=C, читается так: “Все элементы, входящие в состав множества A и множества B, составляют элементы, которые принадлежат множеству C».
Правила нахождения объединения и пересечения и разности множеств
При формировании объединения числовых множеств, следует последовательно записать полностью части одного множества и их дополнить недостающими элементами из остальных. Операцию объединения в отдельных случаях называют сложением множеств и обозначают знаком «+».
Рассмотрим пример объединения числовых множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10}. К имеющимся числовым составляющим множества A 1,2,3,4,5,6,7,8,9 прибавим недостающую часть из множества B 10. Получившееся в результате объединения множество чисел будет выглядеть так {0,1,2,3,4,5,6,7,8,9,10}. Соответственно запись этого объединения:
AUB={0,1,2,3,4,5,6,7,8,9,10}
Чтобы составить пересечение числовых множеств, следует последовательно выбирать части одного множества и удостовериться, входят ли они в другие исследуемые множества, входящие в их число и составляют пересечение.
Для того, чтобы найти пересечение этих же множеств, друг за другом, последовательно проанализируем числа множества A на их наличие в множестве чисел B. Начнём проверку с самого первого числа в множестве A это число 0. В множестве B данное число отсутствует и не войдёт в совокупность пересечения. Смотрим далее, число 1 из множества A так же имеется в составе множества B. Затем следует число 2, которое принадлежит множеству B и, следовательно, пересечению. Идущее за ним 3 не принадлежит A и B не входит в перечисление. Число 4 входит в A и B, значит войдёт и в объединение. Далее продолжаем проверять числа по аналогии. Итак, пересечение множеств A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10} состоит из чисел 2,4,6,8. При записи выглядит так:
AՈB={2,4,6,8}
Выполнение записи пересечения и объединения нескольких множеств
Если требуется выполнить операции с более чем двумя множествами, например: A, B, C, принцип действия подобный предыдущим примерам. В первую очередь находим пересечения A и B. Только затем пересечение полученного множества с C.
Следовательно, процесс нахождения пересечения более двух множеств осуществляется в несколько этапов.
Например, дано три множества A = {1,2,3,7,9}, B = {1,3,5,7,9} и C = {3,4,5,8,9}. Сначала находим пересечение AՈB = {3,9}, затем сравниваем полученное множество с C, это будут те же 3 и 9. Получаем, что пересечение A, B, C выглядит следующим образом:
AՈBՈC={3,9}
При определении объединений двух и более множеств, к числам первого множества последовательно добавляют отсутствующие элементы из второго, третьего и последующих множеств. К примеру, даны следующее множества A = {1,4}, B = {4,3,} и C = {1,3,6,7}. К числовым элементам 1 и 4 из множества A, прибавляем число 4 из множества B. Теперь, к получившемуся множеству 1,3,4 прибавляем цифры 6 и 7 из множества C. В конечном результате получаем объединение:
AUBUC = {1,3,4,6,7}
Для нахождения пересечения совсем не нужно писать много букв. Когда элементов не много, то множество возможно задать элементарным перечислением. Например, первое множество включает в себя числа 1,3,5, второе состоит из элементов 2,3,5. В данном случае, пересечение будет состоять из элементов 3 и 5. Для записи можно использовать прямое перечисление: {1,3,5} Ո {2,3,5} = {3,5}
Основные свойства объединения и перечисления множеств
- Коммутативность или перестановка. Распространяется на все компоненты при любом их количестве.
- AUB = BUA
- AՈB = BՈA
- Ассоциативность или расстановка скобок. Позволяет опускать скобки и делать решение проще.
- (AՈB)ՈC = AՈ(BՈC)
- (AUB)UC = AU(BUC)
- Раскрытие скобок или дистрибутивность.
- (AUB)ՈC=(AՈC)U(BՈC)
- (AՈB)UC=(AUC)Ո(BUC)
Разностью A и B называется множество, которое включает в себя все элементы, каждое из которых принадлежит множеству A и не принадлежит множеству B. Обозначается AB. Приведём пример, найдём разность множеств A = {1,2,3,4,5} и множества B = {2,4,6,8}. Первый вариант находим разность множества A. Запись будет выглядеть так: AB={1,3,5}, в которую не входят элементы, принадлежащие только B числа 6 и 8. Разность множества B при этом выглядит так: BA={6,8}, сюда соответственно не входят числа, принадлежащие только A.
Для закрепления материала пройденных уроков, рассмотрим ещё несколько примеров. Дана задача: A = {0,5,8,10}, B = {3,6,8,9} и X = {0,1,3} Y = {2,4,6}. Найдите пересечение, объединение для A, B и разность множеств X, Y. Решение:
Сначала найдём объединение исходных множеств A U B = {0,3,5,6,8,9,10}.
Затем пересечение A Ո B = {8}
Разность XY = {0,1,3} YX = {2,4,6}
Для того, чтобы выполнить операции над множествами пересечения, объединения, разность в количестве больше двух, следует рассматривать элементы, входящие в первое их них. Затем определить, относится ли этот элемент к каждому из проверяемых множеств. Если данное обстоятельство не соблюдено, то элемент не относится к пересечению. При проверке, лучше выбирать множество с наименьшим количеством элементов в составе.
Кроме перечисленных действий пересечения и объедения существует дополнение множеств и многие другие операции.
Нет времени решать самому?
Наши эксперты помогут!
Отображение множеств с помощью координатной прямой
Для того, чтобы исследовать и обозначать множества, удобно применять выделение числовых промежутков на координатной прямой. Каждая выбранная точка разделяет находящиеся на ней числа на два открытых луча. Приведём пример, точка с координатами 42,7 сформирует промежутки, которые можно записать как (-∞,42,7) и (42,7, +∞). Наше выражение заключено в круглые скобки, это значит, что сама точка 42,7 ни одному из этих промежутков не принадлежит. Числовая прямая, которая записывается как R = (-∞,+∞), при таком варианте из нашего примера, представляет объединение:
(-∞,42,7) U {42,7} U (42,7+∞).
При добавлении нашей рассматриваемой точки 42,7 к одному из представленных (-∞,42,7) или (42,7, +∞) числовых лучей, в таком случае промежуток перестанет быть открытым. При записи выражения нужно будет использовать квадратные скобки, которые обозначают, что точка входит в промежуток. Запись будет выглядеть так: (-∞,42,7] и [42,7+∞). Тем самым множество действительных чисел на координатной прямой будет выглядеть так:
(-∞,42,7] U (42,7+∞) или (-∞,42,7) U [42,7+∞).
На числовой прямой можно выполнять большое количество действий. Такую прямую можно разделить на отрезки не точкой, как в предыдущем примере, а лучом или отрезком. Все выявленные закономерности так же будут соблюдены. Кроме того, они выполняются при разделении самих числовых промежутков. Рассмотрим пример, точка с координатой 18 на промежутке (8,34] разделит его на следующие промежутки (8,18) U {18} U (18,34]. Дополнив точкой, один из промежутков, получатся следующее записи: (8,18] U (18,34], (8,18) U [18,34]. Примем за разделяющую точку цифру 34, которая включается в состав рассматриваемого промежутка и ограничивает его справа. В результате получим объединение множеств {34} и интервала (8,34) либо (8,34] = (8,34) U {34}
Аналогичные закономерности объективны и в ситуации, когда координатная прямая разделяется на промежутки несколькими точками. К примеру, точки -5, 0 и 6 разделят её на промежутки (-∞,-5), (-5,0), (0,6), (6,+∞), при этом множество действительных чисел (-∞,-5) U {-5} U (-5,0) U {0} U (0,6) U {6} U (6,+∞).
Благодаря координатной прямой достаточно просто и легко рассматривать пересечения и объединения множеств. Они указываются друг под другом на координатных прямых с идентичными направлениями отсчёта и точками. При записи отображения множеств координатные прямые обозначают слева квадратной скобкой, фигурные скобки используются, чтобы показать пересечение.
С помощью дополнительной координатной прямой, которую располагают ниже исходной, показываются искомые пересечения или объединение. На ней поперечными чертами отмечают граничные точки первичных множеств, а после выяснения характера точек, их заменяют полями или сплошными. На рисунке вхождение промежутка в объединение показывается штриховкой, отсутствие вхождения – полой точкой, а вхождение – сплошной.
Графически пересечение A и B показывается промежутками, над которыми имеется штриховка, дополненная отдельными точками, которые принадлежат обоим множествам. На рисунке объединение проявляется там, где показана штриховка хотя бы у одного из множеств и сплошные точки.
В приведённых примерах объединения и пересечения множеств указаны только целые числа. Отрезкам на координатной прямой так же принадлежат и другие числа, которые целыми не являются, такие как десятичные дроби. При определении пересечения и определения множеств, класс чисел намного шире, чем представлен в упражнениях, они находятся между целыми числами и количество их очень велико, перечислять которые не представляется возможным.
Лекция 4. Объединение
множеств. Свойства объединения множеств.
Определение. Объединением множеств
А и В называется множество, содержащее все элементы, которые принадлежат
множеству А или множеству В.
Объединение множеств А и В обозначают А∪
В. Таким образом, по определению, А ∪
В = { х | х ∈А
или х∈В}.
Например, если А = { a , c , k , m
, n } и В
= { a , b , c , d , e },
то А ∪
В = { a , c , k , m , n , b , d , e }.
Если изобразить А и В при помощи кругов
Эйлера-Венна, то объединением данных множеств является заштрихованная область
(рис. 4).
Для объединения множеств выполняются
следующие свойства.
1) Переместительное или
коммутативное свойство: А ∪ В = В
∪ А.
2) Сочетательное или
ассоциативное свойство:(А ∪ В)∪
С = А ∪ (В ∪ С).
3) А ∪
∅= А (пустое множество является нейтральным элементом).
4) А ∪
U = U (универсальное множество является поглощающим элементом).
5) Если В ⊂А,
то А∪В = В
Операции объединения и пересечения
множеств связаны законами дистрибутивности или иначе распределительными
свойствами:
(А ∪ В) ∩С
= (А∩С) ∪ (В∩С) и (А∩В) ∪ С =
(А ∪ С) ∩(В ∪ С).
П р и м е р 1. Пусть А – множество
различных букв в слове «математика», а В – множество различных букв в слове
«стереометрия». Найти пересечение и объединение множеств А и В.
Р е
ш е н и е. Запишем множества А и В, перечислив их элементы: А = { м,
а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }.
Буквы м, т, е, и принадлежат и множеству А, и множеству В,
поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е,
и }. В объединение этих множеств войдут все элементы множества А и
несовпадающие с ними элементы из множества В: А ∪
В = { м, а, т, е, и, к, с, р, о, я }.
П р и м е р 2 . В
классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18
человек изучают одновременно английский и немецкий языки. Сколько всего человек
в классе изучают эти иностранные языки? Сколько человек изучают только
английский язык? Только немецкий язык?
Р е ш е н и е. Через А обозначим множество школьников,
изучающих английский язык, через В – множество
школьников, изучающих немецкий
язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18
школьников, поставим это число в пересечение множеств А и В. Английский язык
изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит,
только английский язык изучают 7 человек, укажем это число на диаграмме.
Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9
человек. Поместим и это число на диаграмму. Теперь известно количество
элементов в каждой части множеств, изображенных на диаграмме. Чтобы
ответить на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 =
34. Ответ: 34 человека в классе изучают иностранные языки.
Задания для самостоятельной работы по теме:
1.Найдите объединение множеств А и В, если:
а) А = {26,39,5,58,17,81},
В = {17, 26, 58}.
б) А = {26,39,5,58,
17,81}, В = {17, 26, 58, 5, 39, 81}.
2. Из каких элементов
состоит объединение множества букв в слове «математика» и множества букв в
слове «геометрия»?
3. М – множество
однозначных чисел, Р – множество нечетных натуральных чисел. Из каких
чисел состоит объединение данных множеств? Содержатся ли в нем числа -7 и 9?
4. Используя
координатную прямую, найдите объединение множеств решений неравенств, в которых
х – действительное число:
а) х > -2 и х > 0; в) х > 5 и х
< -7,5;
б) х > -3,7 и х < 4;
г) -2 < х < 4 и х > -1;
д) -7<х<5 и -6<х<2.
Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как
Не понятна формулировка, нашли опечатку?
Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку
Что-то не получается в уроке?
Загляните в раздел «Обсуждение»:
- Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
- Если вопросы остались, задайте свой. Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
- Мы отвечаем на сообщения в течение 2-3 дней. К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
Подробнее о том, как задавать вопросы по уроку

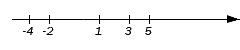













![{displaystyle bigcup limits _{nin mathbb {Z} }[n,n+1]=mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3835f4db48045c5a8bebe8bf50c998c384adab7c)




