Как найти объем бокового сечения конуса

Как найти объем бокового сечения конуса

§ 18. Конус

18.1.Определение конуса и его элементов

Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).

Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.

Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.

Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.

Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).

Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.

Рис. 165

Рис. 166

Рис. 167

Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.

Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что

Sкон = Sбок + Sосн.

Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение  + –  = 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)

18.2. Сечения конуса

Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.

Рис. 168

Рис. 169

Рис. 170

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.

Рис. 171

 Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги. 

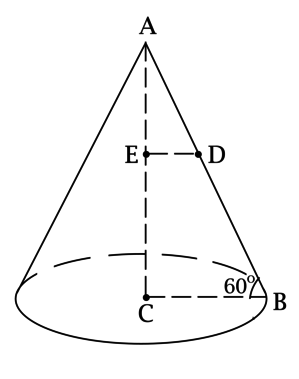
 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.

Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.

Рис. 172

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP = АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС = ; в △ ОСР: CP =  = .

Тогда S△ ABP =  АВ•РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Рис. 173

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Рис. 174

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.

Рис. 175

Рис. 176

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

Sбок =  α•l2,(1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Sбок = πRl.(2)

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

Sкон = πRl + πR2.(3)

Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому

Sбок = 2 π ВС•AD.(4)

Рис. 177

Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем

 = ⇒ BC•AD = DE•АС.(5)

Тогда соотношение (4) принимает вид

Sбок = (2π•DE)•AC,(6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Рис. 178

Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО.  Обозначим этот круг F1.

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

 =  = k,(*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

Sсечен : Sоснов = k2 = : PO2.

Теорема доказана. ▼

18.7.Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

—прямоугольный треугольник (см. рис. 179);

—правильный треугольник (см. рис. 180);

—квадрат (см. рис. 181);

—правильный шестиугольник (см. рис. 182).

Рис. 179

Рис. 180

Рис. 181

Рис. 182

Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).

Рис. 183

Рис. 184

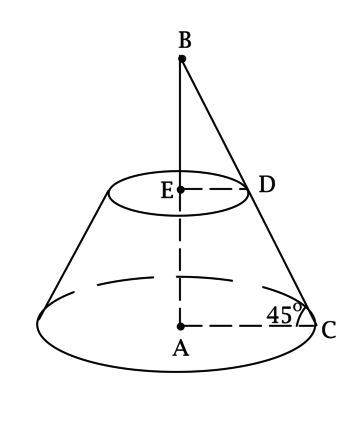
 ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R, OF = R; в △ DPE (правильный): ОР =  = R; в △ ОРF (∠ FOP = 90°):

PF =  = .

Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому

S△ ABP =  AB•PF =  R•  = .

Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда

S1 = 3S△ ABP = ,

S

2 = πR•PA = πR•2R = 2πR2.

Следовательно,

S1 : S2 = : 2πR2 = .

Ответ: а) .


 Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам = •a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl. 

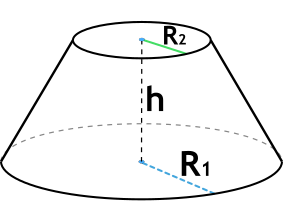
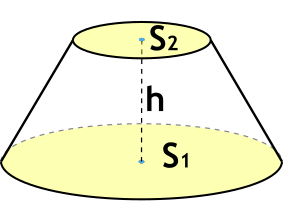
18.8. Усечённый конус

Рис. 185

Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)

Рис. 186

Рис. 187

Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.

Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).

На рисунке 187 показана развёртка усечённого конуса.

Из теоремы 28 следует, что основания усечённого конуса — подобные круги.

Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.

Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.

Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.

Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.

Рис. 188

На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.

18.9. Поверхность усечённого конуса

Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).

Рис. 189

Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).

Используя формулу (2) п. 18.5, получаем

Sбок = πR•PA – πr•РA1 =

= πR(РA1 + А1A) – πr•PA1 =

= πR•A1A + π(R – r)•PA1.

Учитывая, что A1A = l, имеем

Sбок = πRl + π(R – r)PA1.(7)

Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или

R : r = (PA1 + A1A) : PA1, откуда

R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 = .

Подставив это значение РА1 в (7), получаем

Sбок = π(R + r)l.(8)

Таким образом, доказана следующая теорема.

Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼

Площадь полной поверхности усечённого конуса находится по формуле:

Sполн = π•(R + r)•l + π•R2 + π•r2.

Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому

Sбок = 2π•KE•BC.(9)

Рис. 190

Проведём EF ⟂ ВС.  Из подобия прямоугольных треугольников ВСН и EFK имеем

BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)

Тогда равенство (9) принимает вид

Sбок = (2π•EF)•ВH,(11)

т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.

18.10. Объёмы конуса и усечённого конуса

Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).

Рис. 191

Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то  = . Тогда  =  =  = π, значит, для объёмов этих тел выполняется:

Vкон : Vпир = π : 1 или Vкон :  R2•h = π : 1, откуда

Vкон =  πR2 •h.

Рис. 192

Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:

Vус. кон =  π•h•(R2 + r•R + r2).

Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.

Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V =  •h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.

Источник

Напомним,
что конус – это тело, полученное при вращении прямоугольного
треугольника вокруг прямой, проходящей через один из его катетов.

Назовём
элементы конуса.

Осью
конуса называется прямая вращения.

Основание конуса
– круг радиуса ,
который равен катету треугольника вращения.

Радиус
конуса  –
это радиус его основания.

Вершина
конуса – неподвижная вершина треугольника вращения.

Образующая
конуса  –
отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все
образующие конуса равны между собой.

Высота конуса
 –
перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота
конуса совпадает с неподвижным катетом треугольника вращения.

В
конусе радиус основания ,
высота  и
образующая  связаны
следующим соотношением:

.

Сечение
конуса плоскостью, проходящей через его вершину, представляет собой
равнобедренный треугольник, у которого боковые стороны являются образующими
конуса.

Осевым
сечением конуса называется сечение конуса плоскостью,
проходящей через его ось.

Осевое
сечение конуса – равнобедренный треугольник, боковые стороны
которого – образующие, а основание – диаметр основания конуса.

Боковую
поверхность конуса, как и боковую поверхность цилиндра,
можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой
боковой поверхности конуса является круговой сектор.

Обратите
внимание, радиус сектора равен образующей  конуса,
а длина дуги сектора равна длине окружности основания конуса.

Площадь
боковой поверхности конуса можно вычислить по следующим
формулам:

,
,
,

где
 –
длина окружности основания,  –
радиус основания,  –
образующая.

Площадь
полной поверхности конуса равна сумме площади боковой поверхности конуса и
площади его основания.

Тогда
площадь полной поверхности конуса можно вычислить по формуле^

 ,

где
 –
радиус основания конуса,  –
его образующая.

Объём конуса
равен одной третьей произведения площади основания на высоту.

Тогда
его можно вычислить по формуле:

,

где
 –
радиус основания конуса,  –
его высота.

Плоскость,
параллельная плоскости основания конуса, пересекает конус по кругу, а боковую
поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает
конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая
(нижняя) называется усечённым конусом.

Усечённым
конусом называется часть конуса, ограниченная его основанием
и сечением, параллельным плоскости основания. Усечённый конус имеет ось,
высоту ,
радиусы оснований  и
,
образующую .
Осевое сечение усечённого конуса – равнобедренная трапеция.

Площадь
боковой поверхности усечённого конуса и объём усечённого конуса равен разности
площадей боковых поверхностей и объёмов полного конуса и отсечённого.

,

Площадь
боковой поверхности усечённого конуса можно найти по следующим
формулам:

  ,
 

Объём
усечённого конуса можно вычислить по следующим формулам:

 ,

где
 и
 –
площади оснований,  –
высота усечённого конуса;

или
,

где
 –
высота усечённого конуса,  и
 –
радиусы верхнего и нижнего оснований.

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.

Задача
первая. Радиус основания конуса равен  см,
высота конуса равна  см.
Найдите площадь боковой поверхности и объём конуса.

Решение.

Задача
вторая. В конус вписана правильная треугольная пирамида с
площадью основания  см2
и углом наклона бокового ребра к основанию, равным .
Найдите объём и площадь полной поверхности конуса.

Решение.

Задача
третья. В равносторонний конус с радиусом основания, равным см,
вписан прямоугольный параллелепипед в основании которого лежит квадрат, с
высотой  см
так, что одно его основание принадлежит основанию конуса, а вершины другого
основания принадлежат боковой поверхности конуса. Найдите объём
параллелепипеда. В ответе запишите значение .

Решение.

Задача
четвёртая. Длины радиусов оснований и образующей усечённого
конуса равны соответственно  см,
 см
и  см.
Вычислите его высоту.

Решение.

Источник

Объем усеченного конуса через радиусы оснований и высоту

{V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2)}

Радиус нижнего основания R1

Радиус верхнего основания R2

Усеченный конус – фигура, которую можно получить из конуса, если через него провести сечение, параллельное основанию.

Справедливо и другое определение.

Усеченный конус – тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны.

Калькулятор объема конуса и формулы для расчета находится здесь.

Чтобы найти объем усеченного конуса необходимо знать три его характеристики – высоту (h), радиус нижнего основания (R1) и радиус верхнего основания (R2). Кроме того существует вторая формула объема усеченного конуса, для которой необходимо знать высоту конуса, а также площади его верхнего и нижнего оснований.

Содержание:
  1. калькулятор объема усеченного конуса
  2. формула объема усеченного конуса через радиусы оснований и высоту
  3. формула объема усеченного конуса через площади оснований и высоту
  4. примеры задач

Формула объема усеченного конуса через радиусы оснований и высоту

Объем усеченного конуса через радиусы оснований и высоту

{V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2)}

h – высота усеченного конуса

R1 – радиус нижнего основания

R2 – радиус верхнего основания

Формула объема усеченного конуса через площади оснований и высоту

Объем усеченного конуса через площади оснований и высоту

{V=dfrac {h}{3} (S_1 + sqrt{S_1 cdot S_2} + S_2)}

h – высота усеченного конуса

S1 – площадь нижнего основания

S2 – площадь верхнего основания

Примеры задач на нахождение объема усеченного конуса

Задача 1

Найдите объем усеченного конуса радиусы оснований которого равны 1см и 2см, а высота равна 3см​.

Решение

Для решения используем формулу объема усеченного конуса через высоту и радиусы оснований. Подставим известные нам значения в формулу и произведем расчет.

V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2) = dfrac {1}{3} pi cdot 3 cdot (2^2 + 2 cdot 1 + 1^2) = dfrac {1}{3} pi cdot 3 cdot (4 + 2 + 1) = dfrac {1}{3} pi cdot 3 cdot 7 = dfrac {1}{3} pi cdot 21 = dfrac {21}{3} pi = 7 pi : см^3 approx 21.99115 : см^3

Ответ: 7 pi : см^3 approx 21.99115 : см^3

Полученный ответ легко проверить с помощью калькулятора .

Источник

Площадь поверхности конуса

Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.

Площадь боковой поверхности конуса вычисляется по формуле: S = πRl, где R — радиус основания конуса, а l — образующая конуса.

Так как площадь основания конуса равна πR2 (как площадь круга), то площадь полной поверхности конуса будет равна: πR2 + πRl = πR (R + l ).

Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.

Получим ряд равных треугольников. Площадь каждого треугольника равна ah/2 , где а — длина основания треугольника, a h — его высота.

Сумма площадей всех треугольников составит: ah/2 • n = anh/2 , где n — число треугольников.

При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е. an, становится весьма близкой к длине дуги АВ, т. е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.

Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):

S = Cl/2, где С — длина окружности основания конуса, l — образующая конуса.

Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl.

Примечание. В формуле S = Cl/2 поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство

S = Cl/2 точное, а не приближённое.

Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р и l числа, выражающие длины периметра основания и апофемы этой пирамиды.

Тогда боковая поверхность её выразится произведением 1/2р • l .

Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK

1/2р• l, будет стремиться к пределу 1/2С• L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:

S = 1/2С • L = С • 1/2L

Следствия.

1) Так как С = 2πR, то боковая поверхность конуса выразится формулой:

S = 1/2• 2πR • L = πRL

2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:

T = πRL + πR2 = πR(L + R)

Теорема. Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.

Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами р, р1 и l числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.

Тогда боковая поверхность вписанной пирамиды равна 1/2 (р + р1) • l

При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р и р1 стремятся к пределам, принимаемым за длины С и С1 окружностей оснований, а апофема l имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С1) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:

S = 1/2 (С + С1) L

Следствия.

1) Если R и R1 означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:

S = 1/2 (2πR + 2πR1) L = π (R + R1) L.

2) Если в трапеции OO1А1А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:

ВС = 1/2(OA + O1A1) = 1/2 • (R + R1),

откуда

R + R1 = 2ВС.

Следовательно,

S = 2πBC• L,

т. е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.

3) Полная поверхность Т усечённого конуса выразится так:

T = π( R2 + R12 + RL + R1L)

Равна площадь боковой поверхности конуса формула. Площадь боковой и полной поверхности конуса

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.

Мы знаем, что такое конус, попробуем найти площадь его поверхности. Зачем нужно решать такую задачу? Например, нужно понять, сколько теста пойдет на изготовление вафельного рожка? Или сколько кирпичей понадобится, чтобы сложить кирпичную крышу замка?

Измерить площадь боковой поверхности конуса просто так не получится.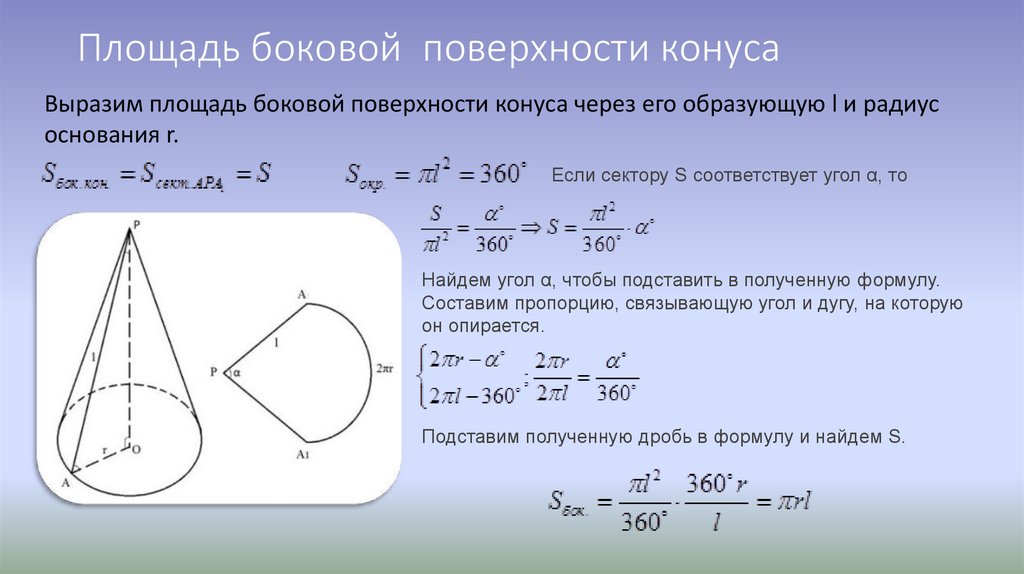 Но представим себе все тот же рожок, обмотанный тканью. Чтобы найти площадь куска ткани, нужно разрезать и разложить ее на столе. Получится плоская фигура, ее площадь мы сможем найти.

Рис. 1. Разрез конуса по образующей

Сделаем так же с конусом. «Разрежем» его боковую поверхность вдоль любой образующей, например, (см. рис. 1).

Теперь «размотаем» боковую поверхность на плоскость. Получаем сектор. Центр этого сектора — вершина конуса, радиус сектора равен образующей конуса, а длина его дуги совпадает с длиной окружности основания конуса. Такой сектор называется разверткой боковой поверхности конуса (см. рис. 2).

Рис. 2. Развертка боковой поверхности

Рис. 3. Измерение угла в радианах

Попробуем найти площадь сектора по имеющимся данным. Сперва введем обозначение: пусть угол при вершине сектора в радианах (см. рис. 3).

С углом при вершине развертки нам придется часто сталкиваться в задачах. Пока же попробуем ответить на вопрос: а не может ли этот угол получиться больше 360 градусов? То есть не получится ли так, что развертка наложится сама на себя? Конечно же, нет.

Докажем это математически. Пусть развертка «наложилась» сама на себя. Это означает, что длина дуги развертки больше длины окружности радиуса . Но, как уже было сказано, длина дуги развертки есть длина окружности радиуса . А радиус основания конуса, разумеется, меньше образующей, например, потому, что катет прямоугольного треугольника меньше гипотенузы

Тогда вспомним две формулы из курса планиметрии: длина дуги . Площадь сектора: .

В нашем случае роль играет образующая ,
а длина дуги равна длине окружности основания конуса, то есть . Имеем:

Окончательно получаем: .

Наряду с площадью боковой поверхности можно найти и площадь полной поверхности. Для этого к площади боковой поверхности надо прибавить площадь основания. Но основание — это круг радиуса , чья площадь по формуле равна .

Окончательно имеем:


,
где — радиус основания цилиндра, — образующая.

Решим пару задач на приведенные формулы.

Рис. 4. Искомый угол

Пример 1
. Разверткой боковой поверхности конуса является сектор с углом при вершине. Найти этот угол, если высота конуса равна 4 см, а радиус основания равен 3 см (см. рис. 4).

Рис. 5. Прямоугольный треугольник, образующий конус

Первым действием, по теореме Пифагора, найдем образующую: 5 см (см. рис. 5). Далее, мы знаем, что .

Пример 2
. Площадь осевого сечения конуса равна , высота равна . Найти площадь полной поверхности (см. рис. 6).

Здесь представлены задачи с конусами, условие связано с его площадью поверхности. В частности в некоторых задачах стоит вопрос об изменении площади при увеличении (уменьшении) высоты конуса или радиуса его основания. Теория для решения задач в . Рассмотрим следующие задачи:

27135. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

Площадь боковой поверхности конуса равна:

Подставляем данные:

75697. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз, а радиус основания останется прежним?

Площадь боковой поверхности конуса:

Образующая увеличивается в 36 раз.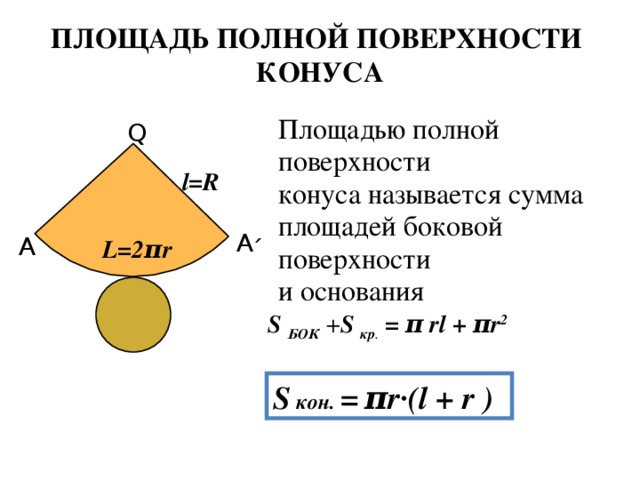 Радиус остался прежним, значит длина окружности основания не изменилась.

Значит площадь боковой поверхности изменённого конуса будет иметь вид:

Таким образом, она увеличится в 36 раз.

*Зависимость прямолинейная, поэтому эту задачу без труда можно решить устно.

27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?

Площадь боковой поверхности конуса равна:

Радиус уменьшается в 1,5 раза, то есть:

Получили, что площадь боковой поверхности уменьшилась в 1,5 раза.

27159. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на Пи.

Полная поверхность конуса:

Необходимо найти радиус:

Известна высота и образующая, по теореме Пифагора вычислим радиус:

Таким образом:

Полученный результат разделим на Пи и запишем ответ.

76299. Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Сечение проходит через середину высоты параллельно основанию. Значит радиус основания и образующая отсеченного конуса будут в 2 раза меньше радиуса и образующей исходного конуса. Запишем чему равна площадь поверхности отсечённого конуса:

Получили, что она будет в 4 раза меньше площади поверхности исходного, то есть 108:4 = 27.

*Так как исходный и отсечённый конус являются подобными телами, то также можно было воспользоваться свойством подобия:

27167. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на Пи.

Формула полной поверхности конуса:

Радиус известен, необходимо найти образующую.

По теореме Пифагора:

Таким образом:

Результат разделим на Пи и запишем ответ.

Задача. Площадь боковой поверхности конуса в четыре раза больше площади основания. Найдите чему равен косинус угла между образующей конуса и плоскостью основания.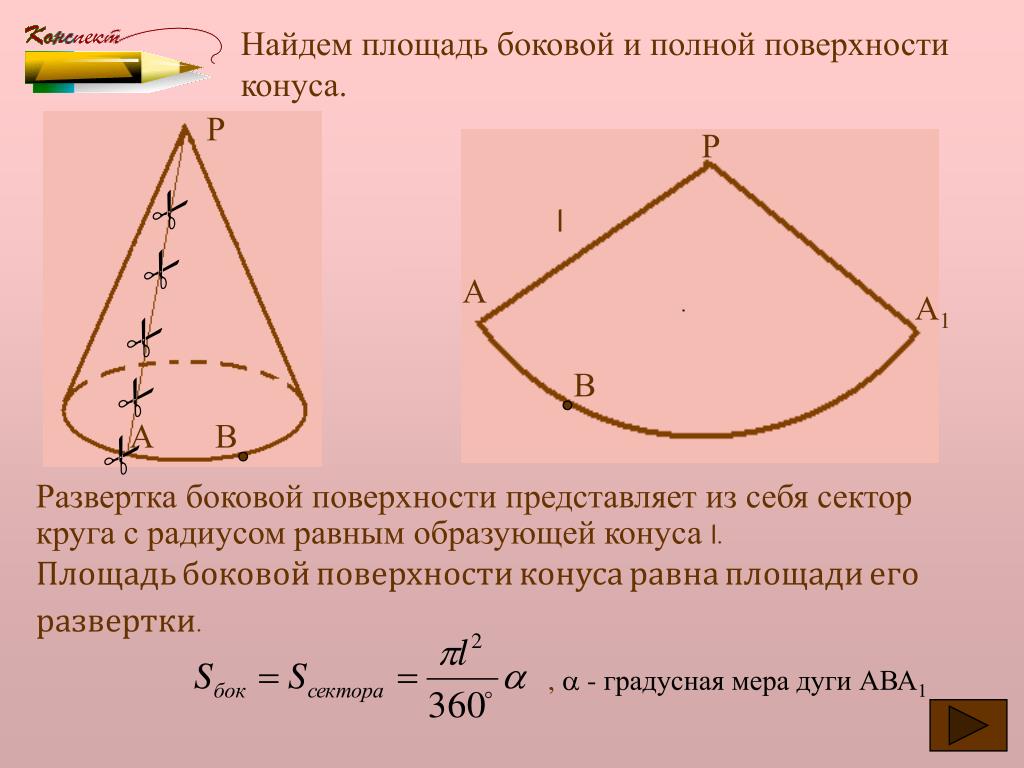

Площадь основания конуса равна:

То есть косинус будет равен:

Ответ: 0,25

Решить самостоятельно:

27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. .

27161. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

На этом всё. Успеха вам!

С уважением, Александр.

*Делитесь с друзьями информацией о сайте через социальные сети.

Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.

Площадь боковой поверхности конуса вычисляется по формуле: S = πRl
, где R — радиус основания конуса, а l
 — образующая конуса.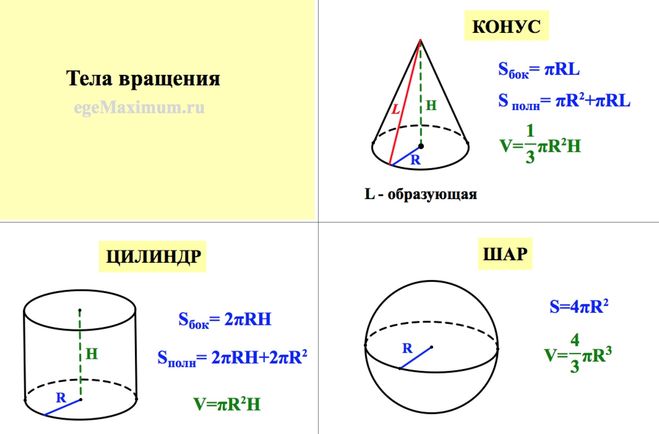

Так как площадь основания конуса равна πR 2 (как площадь круга), то площадь полной поверхности конуса будет равна: πR 2 + πRl
 = πR (R + l
).

Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.

Получим ряд равных треугольников. Площадь каждого треугольника равна ah
 /
 2 , где а
 — длина основания треугольника, a h
 — его высота.

Сумма площадей всех треугольников составит: ah
 /
 2 n
 = anh
 /
 2 , где n
 — число треугольников.

При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е.


an
, становится весьма близкой к длине дуги АВ, т.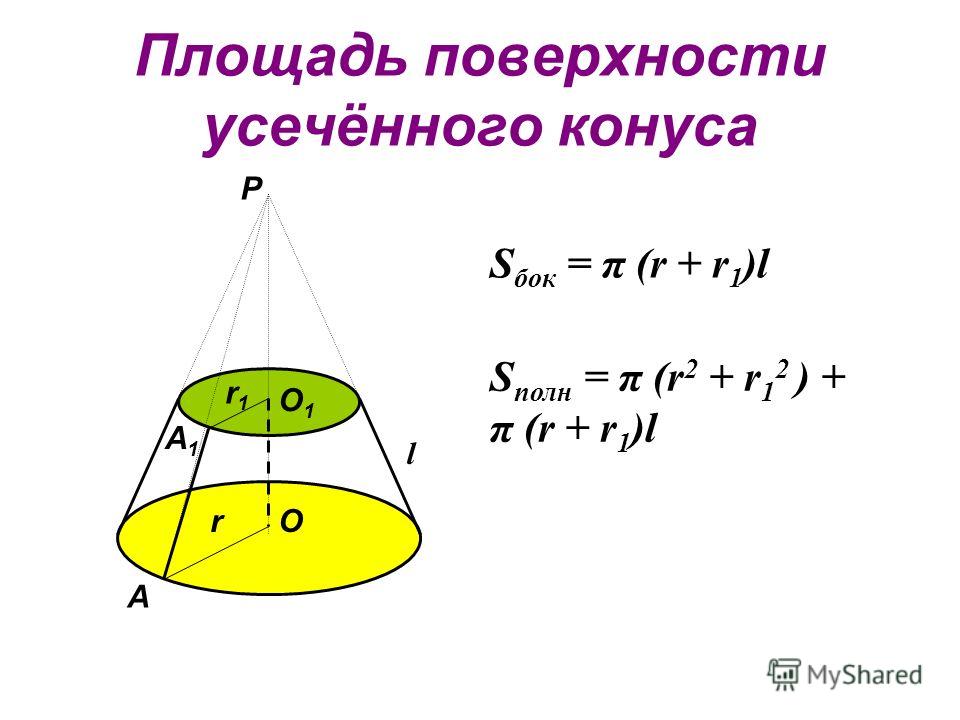 е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.

Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):

S = Cl
 /
 2 , где С — длина окружности основания конуса, l
 — образующая конуса.

Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl
.

Примечание.
 В формуле S = Cl
 /
 2 поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство

S = Cl
 /
 2 точное, а не приближённое.

Теорема.
Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р
 и l
 числа, выражающие длины периметра основания и апофемы этой пирамиды.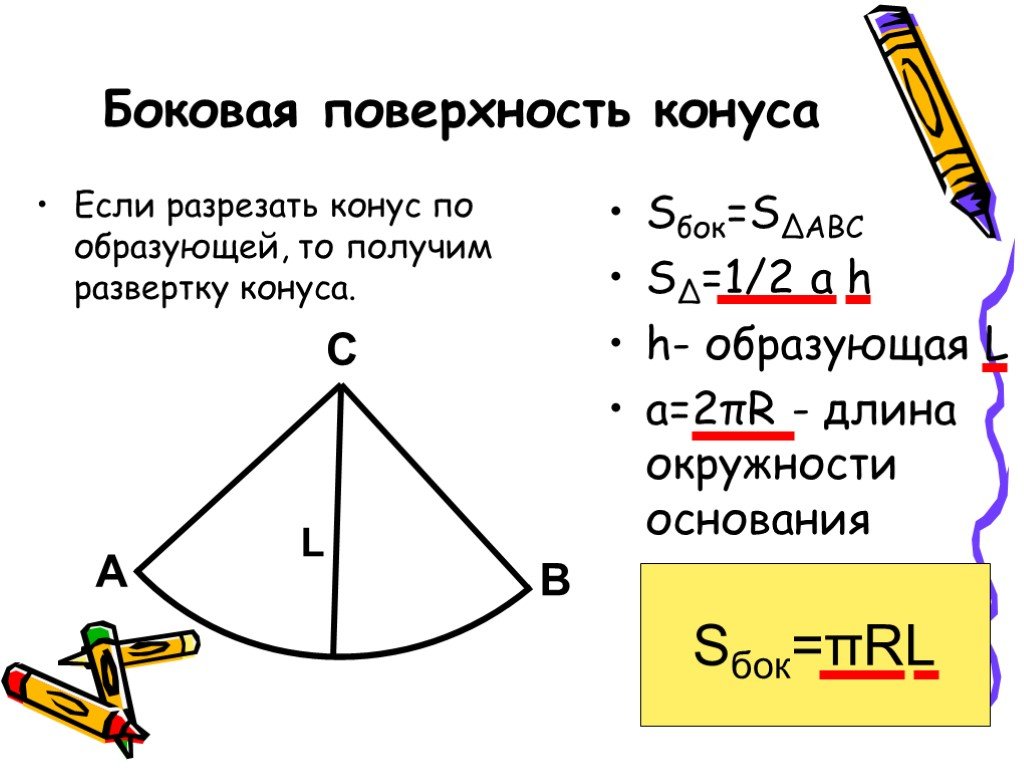

Тогда боковая поверхность её выразится произведением 1 / 2 р
 l
 .

Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р
 будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l
 будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK

1 / 2 р
 l
, будет стремиться к пределу 1 / 2 С
 L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:

S = 1 / 2 С
 L = С
 1 / 2 L

Следствия.

1) Так как С = 2π
 R, то боковая поверхность конуса выразится формулой:

S = 1 / 2
2π
 R
 L = π
 RL

2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:

T = π
 RL + π
 R 2 = π
 R(L + R)

Теорема.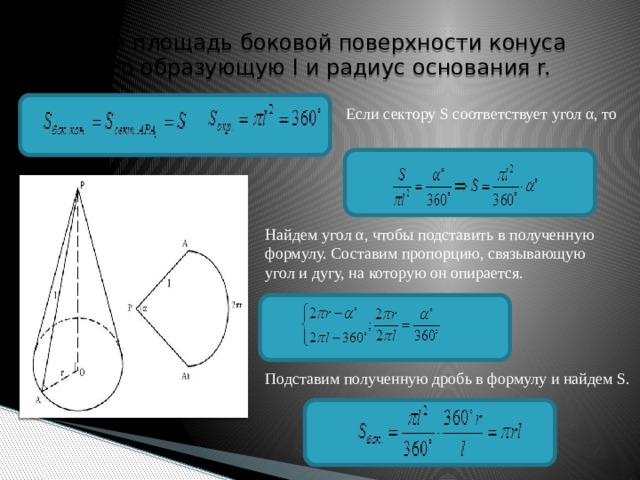
Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.

Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами р, р
 1 и l
 числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.

Тогда боковая поверхность вписанной пирамиды равна 1 / 2 (р + р
 1) l

При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р
 и р
 1 стремятся к пределам, принимаемым за длины С и С 1 окружностей оснований, а апофема l
 имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С 1) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:

S = 1 / 2 (С + С 1) L

Следствия.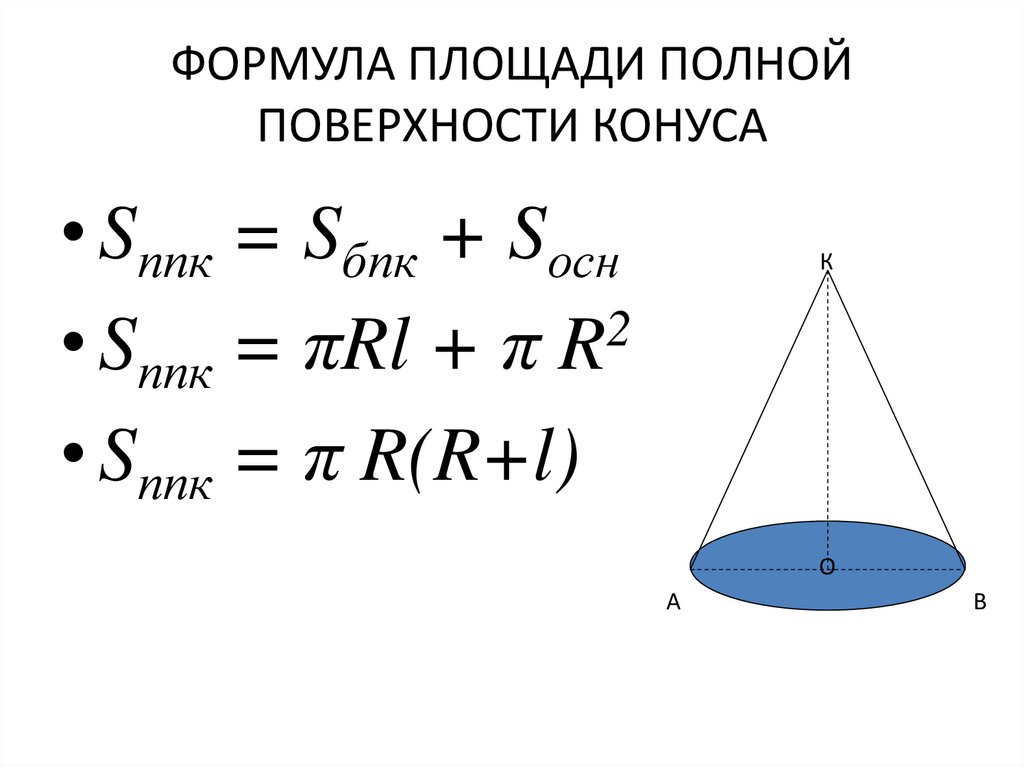

1) Если R и R 1 означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:

S = 1 / 2 (2π
 R + 2π
 R 1) L = π
 (R + R 1) L.

2) Если в трапеции OO 1 А 1 А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:

ВС = 1 / 2 (OA + O 1 A 1) = 1 / 2 (R + R 1),

R + R 1 = 2ВС.

Следовательно,

S = 2π
 BC L,

т. е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.

3) Полная поверхность Т усечённого конуса выразится так:

T = π
(R 2 + R 1 2 + RL + R 1 L)

Боковая площадь конуса

LearnPracticeDownload

Боковая площадь конуса определяется как площадь, покрытая криволинейной поверхностью конуса. Его также называют площадью боковой поверхности (LSA) или площадью криволинейной поверхности (CSA) конуса. Конус — это трехмерный объект, который плавно сужается от плоского круглого основания к точке, называемой вершиной.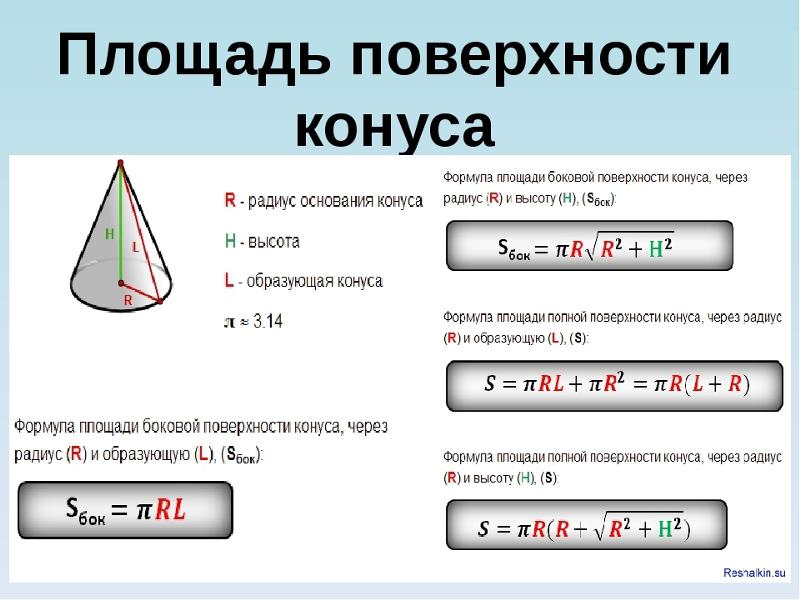 Другими словами, это форма, образованная набором отрезков, исходящих из основания, которые соединяются с общей точкой (вершиной). Эти отрезки начинаются от точек в основании и заканчиваются в вершине.

1. Что такое боковая площадь конуса?
2. Формула боковой площади конуса
3. Как найти боковую площадь конуса?
4. Часто задаваемые вопросы о боковой части конуса

Что такое боковая площадь конуса?

Площадь боковой поверхности конуса представляет собой площадь, занимаемую площадью криволинейной поверхности конуса. Поскольку конус представляет собой трехмерную форму, площадь боковой поверхности конуса также лежит в трехмерной плоскости. Когда много треугольников складываются и вращаются вокруг оси, мы получаем форму, известную как конус. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности.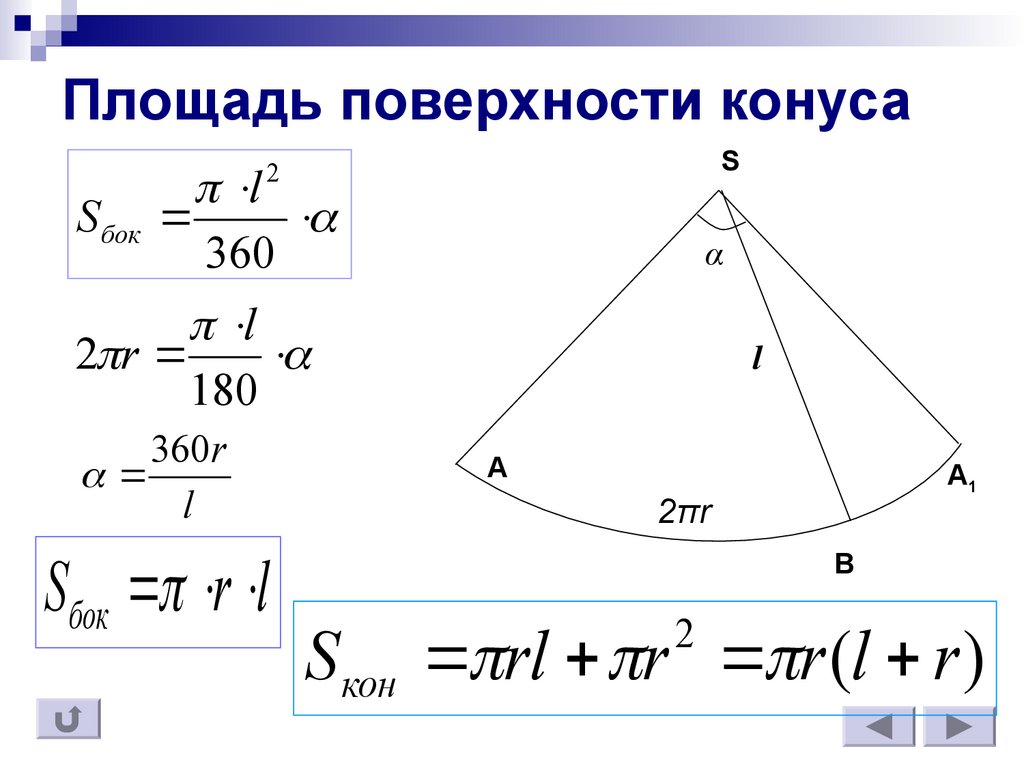 Боковая площадь конуса представлена ​​в квадратных единицах, например, см 2 , м 2 , в 2 и др.

Формула боковой площади конуса

Формула площади боковой поверхности конуса: πrL, где r — радиус основания, а L — наклонная высота. Таким образом, если известны наклонная высота и радиус основания конуса, можно найти площадь его боковой поверхности (или площадь криволинейной поверхности). Мы также можем записать площадь кривизны конуса через высоту конуса, поскольку мы знаем соотношение между высотой и наклонной высотой конуса, используя теорему Пифагора. Связь между высотой и наклонной высотой конуса, заданная как L = √(h 2 + r 2 ), где h — высота конуса. Таким образом, боковая площадь конуса = πrL = πr√(h 2 + r 2 )

Как найти боковую площадь конуса?

Как мы узнали из предыдущего раздела, боковая площадь конуса равна πrL. Таким образом, мы следуем шагам, показанным ниже, чтобы найти боковую площадь конуса:

  • Шаг 1: Определите радиус основания конуса и назовите его r.
  • Шаг 2: Определите его высоту и назовите h.
  • Шаг 3: Найдите площадь боковой поверхности конуса по формуле πrL.
  • Шаг 4: Представьте окончательный ответ в квадратных единицах.

Пример: Чему равна боковая площадь конуса, имеющего радиус основания = 4 единицы и наклонную высоту = 7 единиц?

Решение: При r = 4 единицах и l = 7 единицах

Как мы знаем, боковая площадь конуса = πrL
⇒ Площадь поперечного сечения конуса = (22/7) × 4 × 7 = 88 единиц 2

Ответ: Площадь поперечного сечения конуса составляет 88 единиц 2 .

Решенные примеры на боковой поверхности конуса

  1. Пример 1: Найдите площадь боковой поверхности конуса, имеющего радиус основания 21 единицу и высоту 20 единиц. (Используйте π = 22/7)

    Решение: Учитывая, что r = 21 единица и h = 20 единиц

    Таким образом, наклонная высота конуса, l = √(r 2 + h 2 ) = √(21 2 + 20 2 ) = √(441 + 400) = √841 = 29 ед.
    ⇒ Площадь боковой поверхности конуса = (22/7) × 21 × 29 = 22 × 3 × 29 = 1914 ед. 2

    Ответ:

  2. Пример 2: Найдите боковую поверхность конуса высотой 15 единиц и наклонной высотой 17 единиц. (Используйте π = 3,14)

    Решение: Учитывая, что h = 15 единиц и l = 17 единиц

    Радиус конуса (r) = √(L 2 — h 2 ) = √(17 2 — 30 25 15 ) = √(289 — 225) = √64 = 8 единиц

    Боковая площадь конуса = πrL
    ⇒ Площадь поперечного сечения конуса = 3,14 × 8 × 17 = 427,04 ед.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по боковой поверхности конуса

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о боковой части конуса

Что такое боковая площадь конуса?

Боковая площадь конуса определяется как площадь, покрываемая криволинейной поверхностью конуса.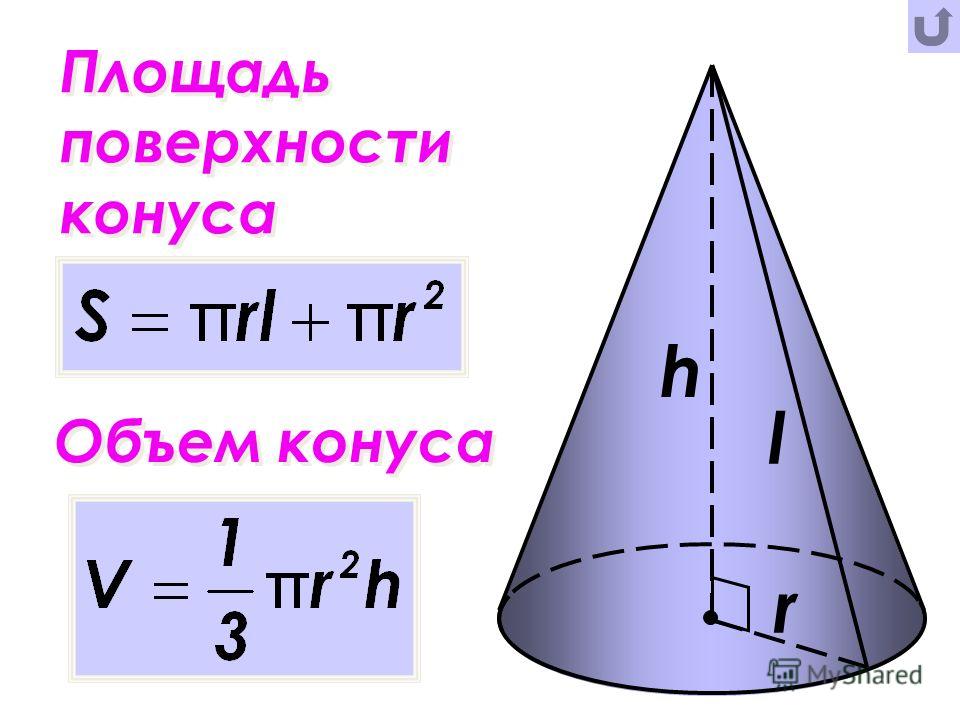 Его также обычно называют площадью боковой поверхности (LSA) или площадью криволинейной поверхности (CSA) конуса. Единица боковой площади конуса выражается в квадратных единицах, например, см 2 , m 2 , in 2 , и т.д.

Какая формула площади боковой поверхности конуса?

Формула площади поперечного сечения конуса определяется как площадь поперечного сечения конуса = πrL, где «r» и «L» — радиус конуса и наклонная высота конуса. Таким образом, можно определить значение боковой площади конуса, если у нас есть значения обоих размеров конуса.

Какова формула площади поперечного сечения конуса через высоту конуса?

Мы знаем, что формула площади поперечного сечения конуса дается как площадь поперечного сечения конуса = πrL. Мы также знаем, что соотношение между наклонной высотой и высотой конуса равно L = √(h 2 + r 2 ). Таким образом, боковая площадь конуса по высоте конуса определяется как πr√(h 2 + r 2 ).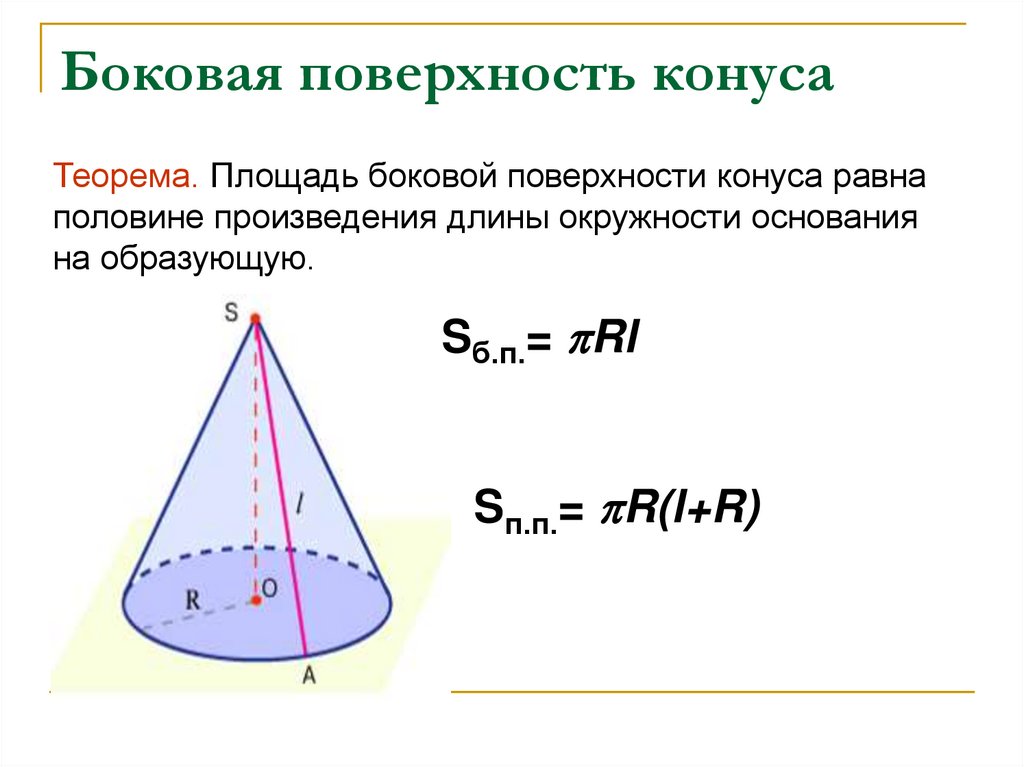

Как найти боковую площадь конуса?

Боковую площадь конуса можно определить с помощью следующих шагов:

  • Шаг 1: Определите радиус основания и высоту конуса.
  • Шаг 2: Определите боковую площадь конуса по формуле πrL.
  • Шаг 3: После того, как значение боковой площади конуса получено, представьте окончательный ответ в квадратных единицах.

Как найти радиус конуса, если известна боковая площадь конуса?

Мы можем найти радиус конуса, если боковую площадь конуса следующие шаги:

  • Шаг 1: Определите заданные размеры конуса и пусть радиус конуса равен «r»
  • Шаг 2: Подставьте значения в формулу πrL и получите уравнение.
  • Шаг 3: Решите уравнение для «r».
  • Шаг 4: После того, как значение радиуса конуса получено, представьте окончательный ответ в единицах.

Что происходит с боковой поверхностью конуса, когда радиус конуса увеличивается вдвое?

Боковая площадь конуса удваивается, когда радиус конуса удваивается, поскольку мы подставляем «2r» вместо «r» в формулу боковой площади конуса. Таким образом, боковая площадь конуса = πrL = π(2r)L = 2(πrL), что в два раза больше первоначального значения боковой площади конуса.

Что происходит с боковой поверхностью конуса, когда наклонная высота конуса уменьшается вдвое?

Боковая площадь конуса уменьшается пополам, когда радиус конуса уменьшается вдвое, поскольку мы подставляем «(L/2)» вместо «L» в формулу боковой площади конуса. Таким образом, боковая площадь конуса = πrL = πr(L/2) = (1/2) × (πrL), что составляет половину первоначального значения боковой площади конуса.

Скачать бесплатные учебные материалы

Рабочий лист на области

Математические листы и
Визуальная учебная программа

Боковая область калькулятора конуса

, созданная Gabriela Diaz

Обзор Laciano Mino

Последний оглавления:

  • Какова формула площади боковой поверхности конуса?
  • В чем разница между боковой площадью и площадью поверхности?
  • Как найти боковую поверхность конуса?
  • Еще больше прямоугольных калькуляторов!
  • Часто задаваемые вопросы

С калькулятором площади поперечного сечения конуса Omni вы сможете определить поперечное сечение правильного конуса в мгновение ока!

Возможно, вам интересно, как найти боковую площадь конуса и даже интересно, есть ли какая-либо разница между его площадью поверхности и боковой площадью, ну, вы попали в нужное место!

Если вы хотите узнать об этом и многом другом, мы приглашаем вас продолжить чтение и найти:

  • Формула боковой площади конуса;
  • В чем разница между боковой площадью и площадью поверхности;
  • Как найти боковую поверхность конуса по его диаметру; и
  • Верно ли, что боковая сторона конуса равна ровно 1/2 площади боковой поверхности цилиндра? 🤔

Какова формула площади боковой поверхности конуса?

Площадь боковой поверхности конуса определяется выражением:

A_L = π x r x √(r² + h²)

Или, с точки зрения наклона конуса:

A_L = π x r x l

Где:

  • A_L — Площадь боковой поверхности;
  • r — Радиус круглого основания конуса;
  • h — вертикаль высота конуса; и
  • l — Наклонная высота.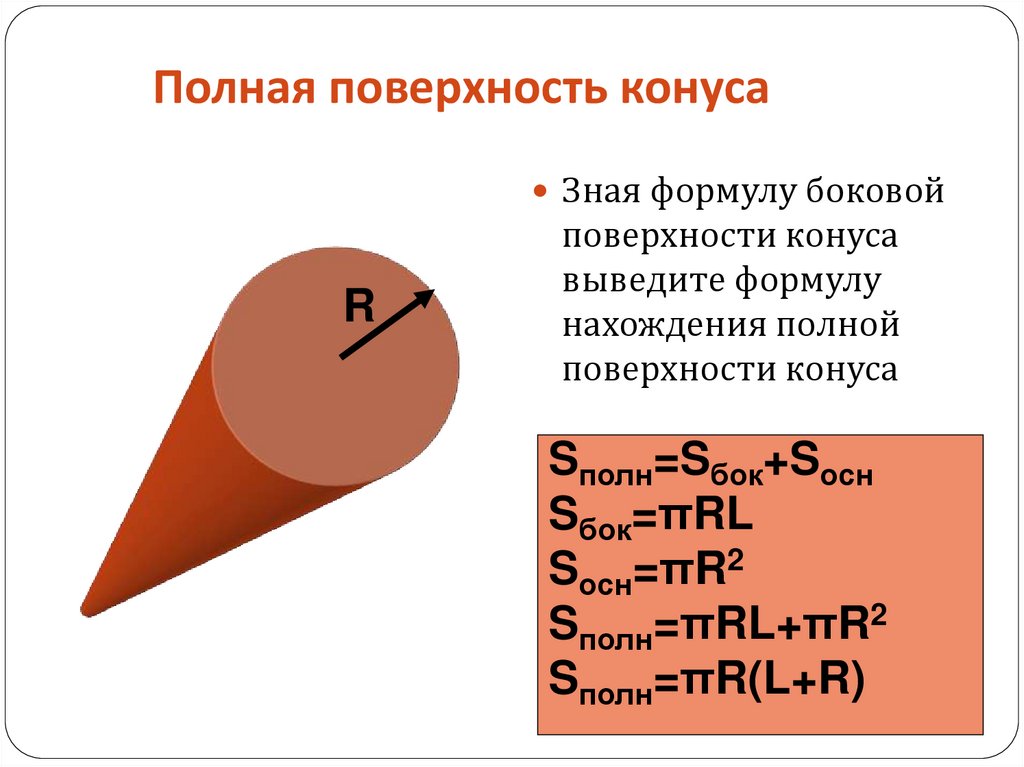

В чем разница между боковой площадью и площадью поверхности?

Из приведенного выше уравнения вы могли заметить, что площадь боковой поверхности конуса не соответствует его общей площади поверхности, определяется как:

A_T = π x r x √(r² + h²) + π x r²

Эти две области состоят в том, что площадь боковой поверхности трехмерной формы является областью, которую можно увидеть при виде сбоку. Это стороны фигуры, исключая ее основание и вершину. Для частного случая конуса мы будем исключать только основание, так как у этой фигуры нет вершины.

Последнее уравнение показывает, что общая площадь поверхности включает боковую площадь π x r x √(r² + h²) и площадь круглого основания конуса π x r² _T =

2

23

Общая площадь = боковая площадь + площадь основания

A_T = π x r x (√(r² + h²) + r)

Отсюда мы можем видеть, что если известна общая площадь и площадь основания конуса , мы могли бы также определить его площадь боковой поверхности как разность между ними:

A_L = Боковая площадь = Общая площадь - площадь основания

Другой вариант расчета боковой площади конуса — это его объем и радиус или объем и вертикальная высота .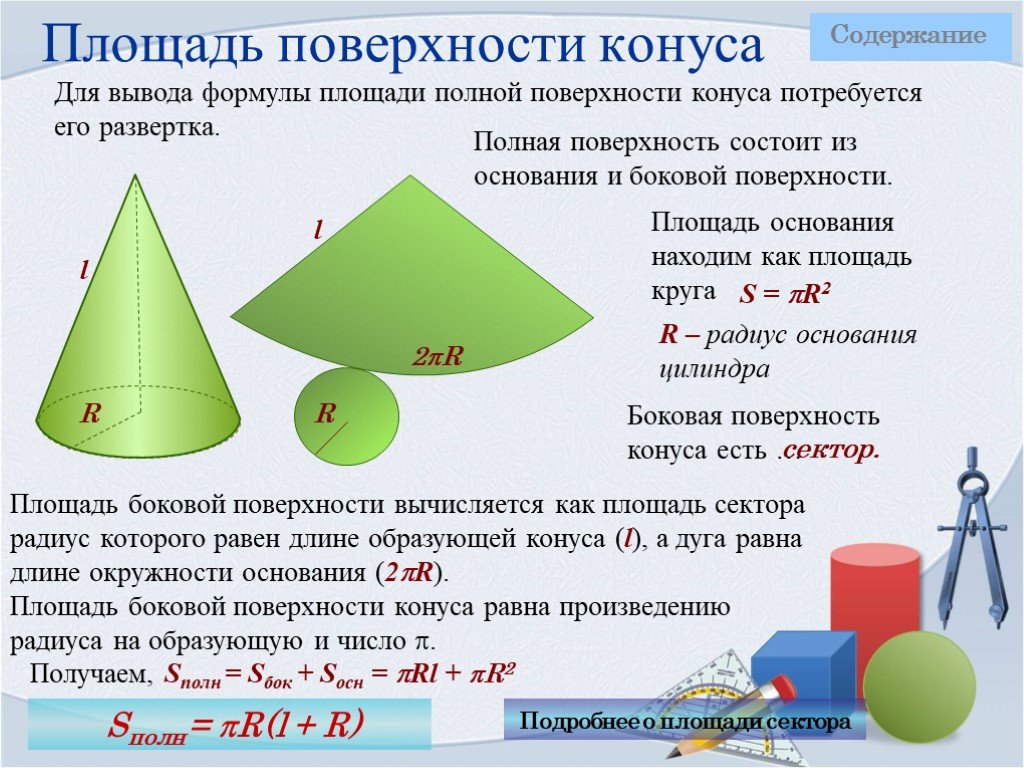 Это означает, что если вы знаете что-либо из этого, калькулятор площади поперечного сечения конуса сможет определить площадь поперечного сечения конуса 😉

Как найти площадь поперечного сечения конуса?

Чтобы найти боковую поверхность конуса:

  1. Используйте формулу площади поперечного сечения конуса, A_L = π x r x √(r² + h²) .
  2. Чтобы использовать эту формулу, вам нужно знать радиус конуса и высоту по вертикали.
  3. Имея эти два известных значения, можно переходить к подстановке значений и выполнению необходимой алгебраической операции.

Например, если у нас есть конус радиусом r = 6 см и высотой h = 10 см, мы можем определить его боковую площадь:

  1. Используя формулу A_L = π x r x √(r² + h²) .
  2. Подставьте соответствующие размеры: A_L = 3,1416 x (6 см) x √((6 см)² + (10 см)²) .
  3. Наконец, выполните необходимые операции и получите результат: A_L = 219,8 см² .

Еще больше прямоугольных калькуляторов!

Если вам понравился калькулятор поперечной площади конуса, и вы хотите узнать больше о геометрических свойствах прямого конуса, мы приглашаем вас посетить другие из наших связанных инструментов:

  • Калькулятор правого кругового конуса;
  • Вычислитель высоты конуса;
  • Расчет радиуса конуса;
  • Расчет высоты наклона конуса; и
  • Калькулятор диаметра конуса.

Часто задаваемые вопросы

Соответствует ли площадь боковой поверхности конуса ровно 1/2 площади боковой поверхности цилиндра?

Правда. Для конуса с наклоном «h» и цилиндра высотой «h», оба с одинаковым радиусом «r», боковая площадь конуса составляет 1/2 боковой площади цилиндра:

  1. Формулы для боковых площадей: A_L_конус = π x r x h и A_L_цилиндр = 2 x π x r x h .
  2. Отсюда 2 x A_L_cone = A_L_цилиндр .

Источник

8. Геометрия в пространстве (стереометрия)


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Задачи по теме «Конус»

(blacktriangleright) Точка (P) – вершина конуса.

(blacktriangleright) Отрезок, соединяющий вершину конуса с границей основания, называется образующей (все образующие равны между собой).

(blacktriangleright) Отрезок, соединяющий вершину конуса с центром основания-круга, является высотой конуса.

(blacktriangleright) Площадь боковой поверхности конуса ({large{S_{text{бок.пов.}}=pi rl}}), где (r) – радиус основания, (l) – образующая.

(blacktriangleright) Площадь полной поверхности конуса – эта сумма площади боковой поверхности и площади основания. [{large{S_{text{полн.пов.}}=pi rl+pi r^2=pi r(r+l)}}]

(blacktriangleright) Объем конуса ({large{V=dfrac{1}{3}S_{text{осн.}}cdot h=dfrac{1}{3}pi
r^2h}}), где (h) – высота конуса.

Заметим, что конус имеет некоторое сходство с пирамидой, только в основании пирамиды лежит многоугольник (граница которого – ломаная), а в основании конуса – круг (граница которого – гладкая).
Поэтому можно сказать, что поверхность пирамиды “ребристая” , а конуса – “гладкая”.


Задание
1

#1886

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности конуса равна (48pi), а площадь основания равна (36pi). Найдите длину образующей конуса.

Если радиус окружности, лежащей в основании конуса обозначить за (r), а длину образующей за (l), то площадь основания и площадь боковой поверхности конуса выразятся по формулам: (S_{text{осн.}} =
pi r^2), (S_{text{бок.пов.}} = pi r l). Из первой формулы следует: (pi r^2 = 36pi) (Rightarrow) (r^2 = 36) (Rightarrow) (r
= 6) (Rightarrow) (6pi l = 48pi) (Rightarrow) (6l = 48) (Rightarrow) (l = 8).

Ответ: 8


Задание
2

#1887

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности конуса равна (48pi), а площадь боковой поверхности усеченного конуса с такими же основанием и углом наклона образующей к плоскости основания равна (36pi). Найдите высоту усеченного конуса, если высота исходного конуса равна (10).

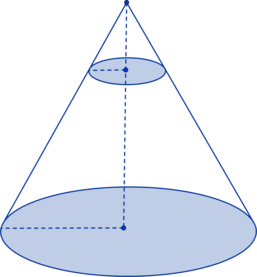
Площадь боковой поверхности меньшего конуса, который дополняет усеченный конус до полного, равна разности их площадей поверхностей: (S_{text{мал}} = 48pi – 36pi = 12pi). Отношение площадей боковых поверхностей большого и малого конусов равно квадрату коэффициента подобия между ними: [frac{S_{text{бол}}}{S_{text{мал}}} = k^2 =
frac{48pi}{12pi} = 4Rightarrow k = 2]

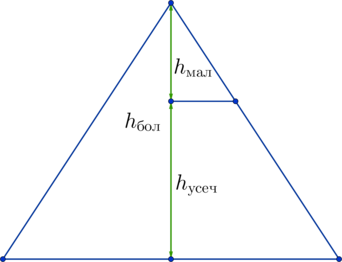
Тогда высоты конусов относятся друг к другу: (dfrac{h_{text{бол}}}{h_{text{мал}}} = dfrac{10}{h_{text{мал}}}
= k = 2). Тогда

[h_{text{мал}} = 5Rightarrow h_{text{усеч}} = h_{text{бол}}
– h_{text{мал}} = 10 – 5 = 5]

Ответ: 5


Задание
3

#962

Уровень задания: Сложнее ЕГЭ

На высоте конуса с вершиной (A), центром основания (C) и радиусом основания (R = 4) отметили точку (E) такую, что расстояние от неё до основания равно (sqrt{3}(4-pi^{-0,5})). Известно, что угол между образующей конуса и плоскостью основания равен (60^circ). Найдите площадь сечения (T) конуса, проходящего через точку (E) и параллельного основанию конуса.

Рассмотрим треугольник (ABC), где (B) – некоторая точка на окружности основания. Так как (AC) – высота конуса, то (ACperp CB), тогда (angle CAB = 90^circ – angle ABC = 30^circ), следовательно, (AB = 2CB = 8). По теореме Пифагора [AC = sqrt{AB^2 – CB^2} = 4sqrt{3}.]

Обозначим через (D) точку пересечения плоскости сечения (T) и (AB). Рассмотрим треугольник (AED): [AE = AC – CE = 4sqrt{3} – sqrt{3}(4 – pi^{-0,5}) = sqrt{dfrac{3}{pi}}.]

Так как сечение (T) параллельно плоскости основания, а (AC) – высота конуса, то (ACperp ED), тогда (triangle AED) – прямоугольный и (angle EAD = 30^circ), откуда [ED = AEcdot mathrm{tg}, angle EAD = sqrt{dfrac{3}{pi}}cdot dfrac{1}{sqrt{3}} = dfrac{1}{sqrt{pi}} = r] – радиус сечения (T).

Таким образом, площадь сечения (T) равна (pi r^2 = picdotdfrac{1}{pi} = 1).

Ответ: 1


Задание
4

#963

Уровень задания: Сложнее ЕГЭ

Радиусы оснований усечённого конуса равны [r = dfrac{2}{sqrt[4]{2}sqrt{pi}}qquad text{и}qquad R = dfrac{10}{sqrt[4]{2}sqrt{pi}},] а угол между его образующей и основанием равен (45^circ). Найдите площадь боковой поверхности этого усечённого конуса.

Обозначим центры оснований усечённого конуса через (A) и (E), так что (A) – центр большего основания. Отметим на большем основании точку (C), а точку меньшего основания, через которую проходит образующая, выходящая из (C), обозначим через (D).

Высота (AE) и образующая (CD) лежат в одной плоскости. Обозначим точку их пересечения через (B).

Так как (AE) – высота, то (AEperp CD) и (AEperp AC).

Рассмотрим прямоугольный треугольник (BAC):
в нём (angle BCA = 45^circ), тогда [AB = R = dfrac{10}{sqrt[4]{2}sqrt{pi}},qquadqquad BC = Rsqrt{2} = dfrac{10sqrt{2}}{sqrt[4]{2}sqrt{pi}}.]

Рассмотрим прямоугольный треугольник (BED):
так как (angle EBD = 45^circ), то [BE = r = dfrac{2}{sqrt[4]{2}sqrt{pi}},qquadqquad BD = rsqrt{2} = dfrac{2sqrt{2}}{sqrt[4]{2}sqrt{pi}},] тогда (EA = AB – BE = R – r), (DC = BC – BD = Rsqrt{2} – rsqrt{2} = sqrt{2}(R – r)). [S_{text{бок}} = pi(R + r)cdot I,] где (I) – образующая, тогда [S_{text{бок}} = pi(R + r)cdotsqrt{2}(R – r) = sqrt{2}pi(R^2 – r^2) = sqrt{2}pileft(dfrac{100}{sqrt{2}pi} – dfrac{4}{sqrt{2}pi}right) = 96.]

Ответ: 96

Старшеклассникам, которые готовятся к сдаче ЕГЭ по математике, непременно стоит научиться вычислять площадь и другие неизвестные параметры конуса. Как показывает практика предыдущих лет, подобные задания из раздела «Геометрия в пространстве» вызывают у выпускников определенные сложности.

При этом понимать, как найти площадь боковой поверхности или, к примеру, сечения конуса, параллельного основанию, должны все учащиеся, независимо от уровня их подготовки. Это позволит им успешно пройти аттестационное испытание по математике.

Базовая информация, которую стоит запомнить

  • Конус представляет собой геометрическое тело, которое образовано совокупностью круга, точки, находящейся вне его плоскости, и лучей, соединяющих заданную точку с точками круга. Его высотой называется перпендикуляр, который опущен из вершины на плоскость основания.
  • Все образующие конуса равны между собой.
  • Осевое сечение конуса представляет собой равнобедренный треугольник. Основание этой фигуры равняется двум радиусам. Боковые стороны треугольника равны образующим конуса.

Занимайтесь вместе с сайтом «Школково»!

Чтобы не допускать распространенных ошибок при решении задач по теме «Конус», выбирайте наш математический портал. Здесь есть весь необходимый материал для изучения разделов, требующих повторения.

Специалисты образовательного проекта «Школково» предлагают новый подход к подготовке к экзамену, предполагающий переход от простого к сложному. Вначале мы даем полную теорию, основные формулы и элементарные практические задачи с решением, в том числе и по теме «Конус», а затем постепенно переходим к заданиям экспертного уровня, которые также встречаются в ЕГЭ. Вся необходимая информация представлена в разделе «Теоретическая справка».

Вы также можете сразу приступить к решению онлайн-задач на вычисление высоты усеченного конуса, площади его боковой поверхности, объема, а также похожих задач на вычисление, например, нахождению объема или площади сечения куба. Большая база упражнений представлена в разделе «Каталог». Перечень заданий систематически обновляется.

Проверьте, насколько легко вы сможете определить площадь конуса в режиме онлайн. Если упражнение потребовало от вас минимальных усилий, рекомендуем вам не тратить время на простые задачи и переходить к более сложным. А если затруднения все же возникли, тогда вам непременно стоит находить время в своем ежедневном расписании на дистанционные занятия вместе со «Школково». С нами вы сможете быстро усвоить алгоритм решения задач на расчет объема конуса и других неизвестных параметров.

УСТАЛ? Просто отдохни

Источник

Добавить комментарий