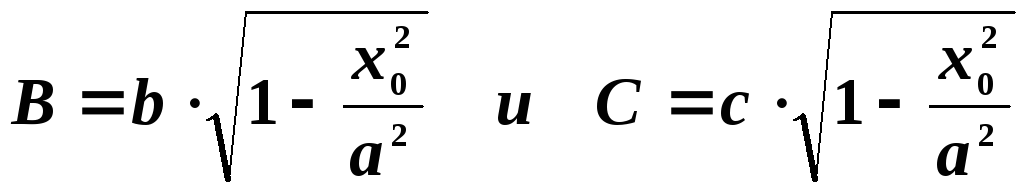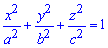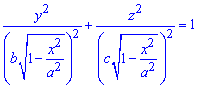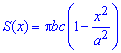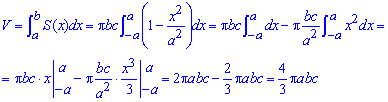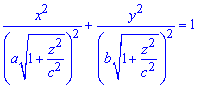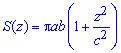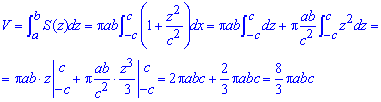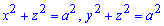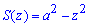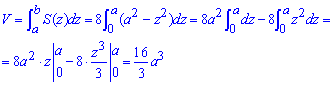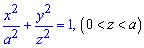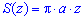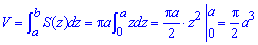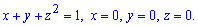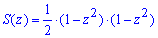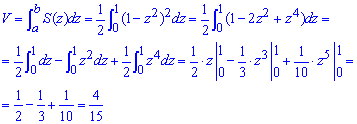Как найти объем через площадь поперечного сечения

Пусть
нам дано тело, известные площади
поперечного сечения
которого расположены перпендикулярно
оси,
как показано на рисунке.

Тогда
элементарный объем этого тела будет
равен

Соответственно
полный объем этого тела будет выражаться
формулой

Например,
найти объем конуса, высоты
и радиуса основания.
Согласно рисунку запишем

Следовательно,
площадь произвольного сечения будет
равна

Тогда
объем конуса будет равен

10. Вычисление объем тела вращения.

Формула
для объема получается из предыдущей,
где
.

Пример 12.
Найти объем эллипсоида с осями
,,.

Имеем уравнение
эллипсоида
.
Для какой-то произвольной точкизапишем

То есть в произвольном
сечении
мы получили эллипс с полуосями

Площадь эллипса
равна

Следовательно,
объем эллипсоида будет равен

1 Y y y y1. Приближенное вычисление определенного интеграла

Пусть
надо вычислить определенный интеграл
от непрерывной на отрезке
функциии при этомпервообразная
нам неизвестна.

Простейший
способ приближенного вычисления
интеграла вытекает из его определения

Эта
формула называется квадратурной формулой
прямоугольников, поскольку площадь
фигуры под графиком функции мы разбиваем
на элементарные прямоугольники.

Можно
площадь фигуры разбивать не на
прямоугольники, а на трапеции, образованные
секущими. В этом случае приближенное
значение интеграла будет рассчитываться
как

FVB

Соседние файлы в папке Лекц.Мат-ка Базов

• #
• #
• #
• #
• #
• #
• #
• #
• #

  19.05.2015694.27 Кб33~WRL2978.tmp

Если объем тела V существует и функция S=S(x) является площадью сечения тела плоскостью (определенная и гладкая на промежутке [a;b]), каторая перпендикулярная к оси Ox в точке x, то объем тела находится за формулой
Это достаточно простая зависимость определенного интеграла, проблема заключается в том, что функция площади не всегда выражается простой зависимостью. В этом Вы скоро убедится из готовых ответов на вычисление объема.
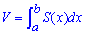
Примеры подобрано из программы для студентов мех-мата Львовского национального университета имени Ивана Франко. Студенты на практических занятиях имеют похожую программу учебы, задания в ряде случаев совпадают.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. “Практикум из математического анализа” (рядом стоит номер из сборника Б. П. Демидовича). 

Для изучения методики нахождения объема тел за известными сечениями основные этапы интегрирования повторяться из примера в пример.

Найти объемы тел, которые ограничены следующими поверхностями

Пример 2463 Найти объем эллипсоида

Вычисление: Сложим уравнение подинтегральной функции. В сечении тела плоскостью, что перпендикулярная к оси Ox, получим эллипс

площадь которого выражается функцией

Определим пределы интегрирования:
у эллипсоида в канонической системе координат это промежуток [-a;a].
Найдем объем эллипсоида:

В том что формула справедлива можете убедиться, сопоставив вычисленную формулу с известной.
Объем фигур измеряется у кубических единиц !
Видим, если эллипсоид вырождается в сферу (a=b=c=R), то его объем равен V=4/3*Pi*R³ (формула известна из “школьной” геометрии).

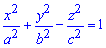
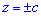
Пример 2464 Найти объем тела (однополий гиперболоид).
Вычисление: Выражаем подинтегральную функцию.
В сечении тела плоскостью, что перпендикулярная к оси Ox, получим эллипс

площадь которого выражается функцией

Определим пределы интегрирования : у эллипсоида в канонической системе координат это промежуток [- a;a].
Найдем объем эллипсоида :

В том что формула справедливая можете убедиться, сравнив вычисленную формулу с известными в справочниках.
Объем фигур измеряется у кубических единиц !
Видим, если эллипсоид вырождается в сферу (a=b=c=R), то его объем равен V=4/3*Pi*R³ (формула известна из “школьной” геометрии).

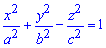
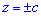
Пример 2464Найти объем тела (однополий гиперболоид).
Вычисление: Выражаемый подинтегральную функцию. В сечении тела плоскостью, что перпендикулярная к оси Oz, получим эллипс

площадь которого

Пределы интегрирования известны за условием: .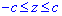
Кроме этого они являются подсказкой в каком направлении выполнять перерез и искать функцию площади.
Найдем объем однополого гиперболоида, что ограничен сверху и снизу плоскостями:

Определенный интеграл в этом задании находится без трудностей.

Пример 2465Найти объем тела образованного пересечением цилиндрических поверхностей
Вычисление: Сложим уравнение подинтегральной функции. Рассмотрим 1/8 часть тела (она расположена в И квадранте).
В сечении плоскостью, какая перпендикулярная к оси Oz, получим квадрат, площадь которого равна

Пределы интегрирования : И вадрат прямоугольной системы координат [0;a].
Интегрированием вычисляем объем тела :

Как можно убедиться из формул площади, их интегрирования достаточно не сложное.

Пример 2468Вычислить объем тела
Вычисление: Выражаемый подинтегральную функцию. В сечении плоскостью, какая перпендикулярная к оси Oz, получим эллипс, площадь которого известна
Пределы интегрирования за условием тоже известны:
.
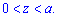
Осталось проинтегрировать и подставить пределы.

Получили, что объем тела равен V=Pi/2*a³ куб. од.

Пример 2469Найти объем тела
Вычисление: Запишем подинтегральную функцию. В сечении плоскостью, которая перпендикулярная к оси Oz, получим равнобедренный прямоугольный треугольник с катетом длиной 1-z², площадь которого легко находится

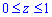
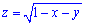
Пределы интегрирования : (это видно из области существования функции ).
Объем тела находим интегрированием:

Из приведенных примеров Вы могли заметить, что все зависит от уравнения площади сечения. Для того, чтобы его записать нужно владеть добрым пространственным воображением и знать сечения основных пространственных тел. Все остальное зависит от Вашего умения интегрировать.

Макеты страниц

Enter the total cross-sectional area (ft^2) and the length of section (ft) into the Volume From Cross-Section Calculator. The calculator will evaluate and display the Volume From Cross-Section. 

• All Volume Calculators
• Surface Area to Volume Calculator
• Volume Fraction Calculator
• Change in Volume Calculator

Volume From Cross-Section Formula

The following formula is used to calculate the Volume From Cross-Section. 

• Where Vc is the Volume From Cross-Section (ft^3)
• CSA is the total cross-sectional area (ft^2) 
• L is the length of section (ft) 

To calculate volume from a cross-section, multiply the cross-sectional area by the length.

How to Calculate Volume From Cross-Section?

The following example problems outline how to calculate Volume From Cross-Section.

Example Problem #1:

1. First, determine the total cross-sectional area (ft^2). 
   1. The total cross-sectional area (ft^2) is given as:  250.
2. Next, determine the length of section (ft). 
   1. The length of section (ft) is provided as: 4.
3. Finally, calculate the Volume From Cross-Section using the equation above: 

Vc = CSA * L

The values given above are inserted into the equation below:

Vc = 250 * 4 = 1000 (ft^3)

Example Problem #2: 

The variables needed for this problem are provided below:

total cross-sectional area (ft^2) = 300

length of section (ft) = 9

Entering these values and solving gives:

Vc = 300*9 = 2700 (ft^3)