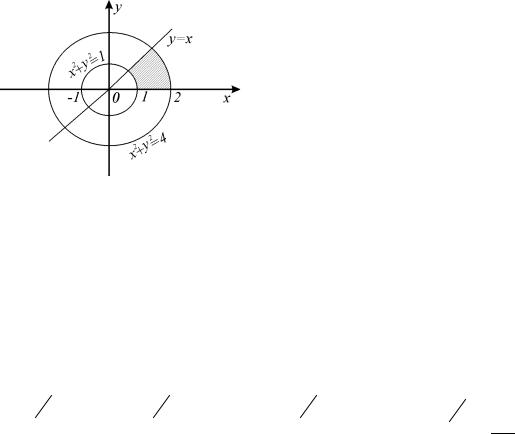
Пример 1.8. Найти площадь области D , ограниченной окружностями x2 + y2 =1 и x2 + y2 = 4 и прямыми x = y и y = 0, y ≥ 0.
Решение. Так как область D (рис. 1.13) есть часть круга, то площадь ее области вычислим по формуле (1.14), то есть воспользуемся полярными координатами. Пределы внешнего интеграла по переменной ϕ
|
определяются |
прямыми: |
y = 0 , |
||
|
следовательно, |
ϕ = 0 |
и |
y = x , |
|
|
следовательно, |
ϕ = π . |
Пределы |
||
|
4 |
||||
|
внутреннего интеграла по переменной ρ |
||||
|
определим так: фиксируем произвольное |
||||
|
Рис. 1.13 |
значение ϕ (0, |
π |
полюса О |
|
|
4 ) , затем |
из |
под углом ϕ проведем луч. Точка входа этого луча в область D лежит на
дуге окружности x2 + y2 = 4, уравнение которой в полярных координатах ρ = 2, а точка выхода этого луча из области D лежит на дуге окружности
x2 + y2 =1, уравнение которой в полярных координатах ρ =1. Значит, пределами интегрирования по ρ, соответственно, будут 1 и 2. Поэтому
|
π 4 |
2 |
π 4 |
ρ |
2 |
2 |
1 |
π 4 |
3 |
π |
4 |
|||||||
|
S = ∫ |
dϕ∫ρdρ = ∫ |
dϕ |
= |
∫(4 |
−1)dϕ = |
ϕ |
|||||||||||
|
2 |
2 |
2 |
0 |
||||||||||||||
|
0 |
1 |
0 |
1 |
0 |
|||||||||||||
2. ТРОЙНЫЕ ИНТЕГРАЛЫ
Тройной интеграл является аналогом двойного интеграла и вводится для функций трех переменных.
2.1. Определение тройного интеграла. Пусть функция f (x, y, z)
определена в ограниченной замкнутой области V . Разобьем эту область с помощью сети поверхностей на конечное число частичных областей
|
V1,V2 ,…Vn , объемы которых соответственно |
обозначим |
через |
||
|
∆v1, ∆v2,…∆vn . В каждой частичной области |
Vi , i = |
|||
|
1, n |
выберем |
16

произвольную точку M i (xi , yi , zi ) , i =1, n и умножим значение функции f (x, y, z) в точке Mi на объем∆vi этой области, а затем составим сумму
|
n |
|
|
σn = ∑ f (xi , yi , zi )∆vi , |
(2.1) |
i =1
которая называется интегральной суммой для функции f (x, y, z) по об-
ласти V .
Если существует конечный предел I интегральной суммы (2.1) при стремлении к нулю наибольшего λ из диаметров всех частичных областей
|
Vi , i = |
, |
зависящий ни от способа разбиения области V , ни от |
|||||||
|
1, n |
не |
||||||||
|
выбора |
точек |
Mi (xi , yi , zi ), то этот предел называется тройным |
|||||||
|
интегралом |
функции |
f (x, y, z) по |
области V и |
обозначается |
так |
||||
|
∫∫∫ f (x, y, z)dv . Таким образом, по определению |
|||||||||
|
V |
n |
||||||||
|
I = lim |
∑ f (xi , yi , zi )∆vi = ∫∫∫ f (x, y, z)dv . |
(2.2) |
|||||||
|
λ→0 i =1 |
V |
||||||||
|
Функция |
f (x, y, z) называется в |
этом случае |
интегрируемой по |
||||||
|
области |
V , |
V |
– областью интегрирования, x, y, z – переменными |
||||||
|
интегрирования, dv – элементом объема, а λ = max d (Vi ) . |
|||||||||
|
1≤i≤n |
Если разбиение области V на частичные области проводить плоскостями, параллельными координатным плоскостям (в дальнейшем
будем предполагать, что это всегда имеет место), то частичные области Vi
|
– |
есть |
прямоугольные |
параллелепипеды |
и, |
следовательно, |
||
|
∆vi |
= ∆xi ∆yi ∆zi , i = |
. Тогда dv = dxdydz и |
|||||
|
1, n |
I = ∫∫∫ f (x, y, z)dv = ∫∫∫ f (x, y, z)dxdydz.
|
V |
V |
|
|
Замечание 2.1. Если в (2.2) положить f (x, y, z) ≡1 при (x, y, z) V , |
||
|
то получим |
выражение |
для объема V области V в виде тройного |
|
интеграла |
V = ∫∫∫dxdydz . |
|
|
V |
||
|
# |
||
|
Достаточные условия существования тройного интеграла можно |
||
|
сформулировать в виде следующей теоремы. |
||
|
Теорема. Всякая непрерывная в замкнутой ограниченной области |
||
|
V функция |
f (x, y, z) интегрируема в этой области. |
17
Замечание 2.2. Можно указать менее жесткие условия существования тройного интеграла. Но мы ограничимся рассмотрением только непрерывных в замкнутой области функций.
#
Тройные интегралы обладают свойствами, аналогичными свойствам двойных интегралов (см. пункт 1.2).
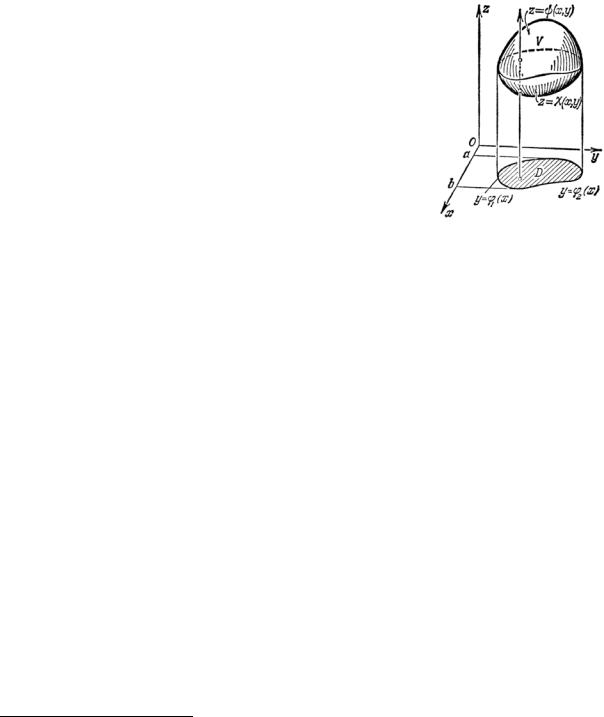
2.2. Вычисление тройных интегралов сводится к трехкратному интегрированию, то есть к последовательному вычислению трех
|
обыкновенных |
(однократных) |
определенных |
|||||
|
интегралов по каждой из трех переменных |
|||||||
|
координат точки трехмерного пространства. |
|||||||
|
Пусть |
функция |
f (x, y, z) |
непрерывна |
в |
|||
|
области V . Пусть поверхность S , ограничивающая |
|||||||
|
тело V , пересекается не более, чем в двух точках |
|||||||
|
любой |
прямой, |
параллельной |
одной |
из |
|||
|
координатных осей1, например, оси Oz, и |
|||||||
|
проходящей через любую внутреннюю точку |
|||||||
|
области (рис. 2.1), и проектируется в правильную |
|||||||
|
двумерную область D плоскости xOy .Такая |
Рис. 2.1 |
||||||
|
область |
V |
называется |
правильной трехмерной |
|
областью. Пусть нижняя часть поверхности |
S задана |
уравнением |
||||
|
z = χ( x, y ), верхняя – уравнением |
z =ψ(x, y) , |
где |
χ(x, y),ψ(x, y) – |
|||
|
однозначные непрерывные функции, определенные в |
областиD , |
|||||
|
являющейся проекцией тела V на плоскостьxOy . Тогда |
||||||
|
ψ ( x, y) |
||||||
|
∫∫∫ f (x, y, z)dxdydz = ∫∫dxdy |
∫ f (x, y, z)dz , |
(2.3) |
||||
|
V |
D |
χ( x, y) |
||||
|
ψ ( x, y) |
||||||
|
причем сначала вычисляется |
внутренний интеграл |
∫ f (x, y, z)dz по |
||||
|
переменной z , в котором переменные x |
χ( x, y) |
|||||
|
и |
y считаются постоянными, а |
|||||
|
пределы интегрирования есть |
функции |
от |
x и |
y , |
а затем внешний |
двойной интеграл по области D .
Если область D является правильной в направлении оси Oy , то интеграл по области V вычисляется по формуле
|
b |
ϕ2 ( x) |
ψ( x, y) |
||
|
∫∫∫ f (x, y, z)dxdydz = ∫dx |
∫ |
dy ∫ f (x, y, z)dz, |
(2.4) |
|
|
V |
a |
ϕ1 ( x) |
χ( x, y) |
1 Более сложные области V часто удается сводить к рассматриваемому виду путем разбиения их на конечное число областей V1,…,Vn, каждая из которых удовлетворяет условиям, изложенным выше.
18
то есть сводится к последовательному вычислению трех определенных интегралов. В (2.4) сначала вычисляется внутренний интеграл по переменной z при постоянных x и y , затем внутренний интеграл по
переменной y при постоянной x и, наконец, интеграл по переменнойx –
пределы интегрирования внешнего интеграла постоянны.
Разумеется, порядок интегрирования, при выполнении известных условий может быть избран другим, как в двойном интеграле по области D в формуле (2.4)
|
d |
ψ2 ( y) |
ψ( x, y) |
||
|
∫∫∫ f (x, y, z)dxdydz = ∫dy ∫ |
dx ∫ f (x, y, z)dz, |
(2.5) |
||
|
V |
c |
ψ1 ( y) |
χ( x, y) |
|
|
также и в тройном интеграле: для этого тело V нужно проектировать на |
||||
|
плоскость yOz или на плоскость |
xOz , |
тогда в (2.3) соответственно |
||
|
поменяются |
ролями переменные x , |
y , z . |
Наиболее простой вид формула вычисления тройного интеграла принимает в случае, когда V есть прямоугольный параллелепипед, ограниченный плоскостями x = a, x = b, y = c, y = d, z = e, z = h :
|
b |
d |
h |
||
|
∫∫∫ f ( x, y, z )dxdydz = ∫dx∫dy∫ f ( x, y, z )dz. |
(2.6) |
|||
|
V |
a |
c |
e |
|
|
Пример 2.1. Вычислить |
∫∫∫( x + z )dxdydz по |
области V, |
V
ограниченной плоскостями x = 0, x = 1, y = 0, y = 1, z = 0, z = 1. Решение. Так как область интегрирования есть прямоугольный
параллелепипед, то для вычисления данного интеграла воспользуемся формулой (2.6)
|
1 |
1 |
1 |
1 |
1 |
z2 |
1 |
|||||||||||||
|
∫∫∫(x + z)dxdydz = ∫dx∫dy∫(x + z)dz = ∫dx∫dy(xz + |
) |
= |
|||||||||||||||||
|
2 |
|||||||||||||||||||
|
V |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||||||
|
1 |
|||||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
x2 |
x |
1 |
||||||||||
|
= ∫dx∫( x + |
)dy = ∫dx(x + |
) y |
= ∫(x + |
)dx = ( |
+ |
) |
=1. |
||||||||||||
|
2 |
2 |
2 |
2 |
2 |
|||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||
|
Пример.2.2. Вычислить∫∫∫ |
x2dxdydz по области V , ограниченной |
||||||||||||||||||
|
плоскостями z = 0, |
x = 0, |
V |
x + y + z −2 = 0. |
||||||||||||||||
|
y = 0, |
Решение. Область интегрирования V есть тетраэдр, расположенный в первом октанте (рис.2.2). Область V является правильной, так как прямая, проведенная через любую ее внутреннюю точку параллельно оси Oz пересекает поверхность ограничивающую пространственную область лишь в двух точках (рис.2.2), поэтому для вычисления заданного интеграла воспользуемся формулой (2.3).
19
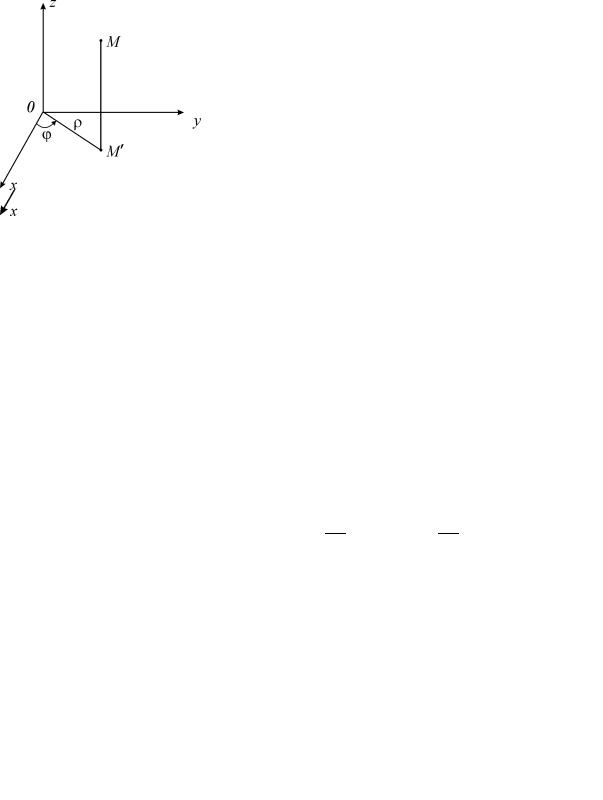
Рис. 2.3
|
Определим пределы внутреннего интеграла по |
||
|
переменной |
z . Так как прямая, |
параллельная оси |
|
Oz , входит в область V |
через плоскость, |
|
|
уравнение |
которой z = 0 |
(нижний предел |
|
интегрирования), а выходит из области через |
||||
|
плоскость, уравнение |
которой |
z = 2 − x − y |
||
|
(верхний предел интегрирования), то |
||||
|
2−x−y |
||||
|
∫∫∫x2dxdydz = ∫∫dxdy |
∫x2dz , |
|||
|
V |
D |
0 |
||
|
где D – проекция области V на плоскость xOy. D |
Рис. 2.2 |
|||
|
есть треугольник, образованный прямыми |
||||
x = 0, y = 0 и y = 2 − x . Следовательно, по формуле (2.4) имеем
|
2−x−y |
2 |
2−x |
2−x −y |
2 |
2−x |
02−x −y = |
||||||||||
|
∫∫dxdy |
∫x2dz = ∫x2dx ∫ |
dy |
∫dz = ∫x2dx ∫dy z |
|||||||||||||
|
D |
0 |
0 |
0 |
0 |
0 |
0 |
2−x |
|||||||||
|
2 |
2−x |
2 |
y |
2 |
||||||||||||
|
= ∫x2dx ∫(2 − x − y)dy = ∫x2dx ((2 − x) y − |
) |
= |
||||||||||||||
|
0 |
0 |
0 |
2 |
0 |
||||||||||||
|
2 |
||||||||||||||||
|
2 |
(2 − x) |
2 |
x |
4 |
||||||||||||
|
= ∫x2 ((2 − x)2 − |
)dx = ∫(2x2 − 2x3 + |
) dx = |
||||||||||||||
|
2 |
||||||||||||||||
|
0 |
0 |
2 |
||||||||||||||
|
= ( |
2x3 |
− |
2x |
4 |
+ |
x5 |
) |
2 |
||
|
3 |
4 |
10 |
0 |
|||||||
= 163 −8 +165 = 158 .
#
2.3. Тройной интеграл в цилиндрических координатах. Как и в двумерном случае, для тройных интегралов имеют место формулы преобразования интеграла от прямоугольных координат к новым системам координат. Наиболее употребительные из них – цилиндрические и сферические координаты. Мы рассмотрим только преобразование к цилиндрическим координатам.
В цилиндрической системе координат положение точки M пространства определяется полярными координатами ϕ и ρ точки M ′ (проекции точки
Mна плоскость xOy ) и аппликатой z самой точки M (рис. 2.3). Числа
ϕ, ρ, z называют цилиндрическими координатами точки M , причем
20
ρ ≥ 0, ϕ [0,2π] z – любое. Цилиндрические координаты связаны с
|
декарторыми соотношениями: |
|
|
x = ρ cosϕ, y = ρ sin ϕ, z = z . |
(2.7) |
|
Преобразование тройного интеграла от декартовых |
координат |
x , y, z к цилиндрическим координатам ϕ, ρ, z осуществляется по
следующей формуле перехода
∫∫∫ f (x, y, z)dxdydz =∫∫∫ f (ρ cosϕ, ρsin ϕ, z)ρdρdϕdz ,
V V
где dv = ρdρdϕdz – элемент объема в цилиндрических координатах.
Выразим уравнения нижней и верхней частей поверхности S , ограничивающей данную область V , в цилиндрических координатах –
z = z1(ρ,ϕ) и z = z2 (ρ,ϕ) соответственно и запишем формулу для вычисления интеграла в цилиндрических координатах, аналогичную (2.3)
|
∫∫∫ f (ρ cosϕ, ρsinϕ, z)ρdρdϕdz = ∫∫ρdρdϕ |
z2 ( ρ,ϕ) |
|||
|
∫ f (ρ cosϕ, ρsinϕ, z)dz, |
||||
|
V |
D |
z1 ( ρ,ϕ) |
||
|
где D есть проекция области V на плоскость xOy.Воспользовавшись |
||||
|
заданием плоской области D в полярных координатах (пункт 1.4) получим |
||||
|
z2 |
( ρ,ϕ) |
|||
|
∫∫ρdρdϕ |
∫ f (ρ cosϕ, ρsinϕ, z)dz = |
|||
|
D |
z1 ( ρ,ϕ) |
|||
|
β |
ρ2 (ϕ) |
z2 ( ρ,ϕ) |
||
|
= ∫dϕ |
∫ ρdρ |
∫ f (ρ cosϕ, ρsinϕ, z)dz . |
(2.8) |
αρ1 (ϕ) z1 ( ρ,ϕ)
Формулу (2.8) удобно использовать, если область V проектируется в круг или часть круга.
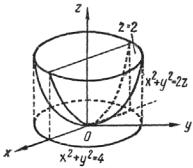
Пример 2.3. Вычислить ∫∫∫(x2 + y2 )dxdydz по области, ограни-
V
ченной плоскостью z = 2 и параболоидом x2 + y2 = 2z.
Решение. Область V (рис. 2.4) снизу ограничена параболоидом x2 + y2 = 2z , сверху
плоскостью z = 2 . Эта область проектируется на плоскость xOy в облстьD , ограниченную
|
окружностью |
x2 + y2 = 4, |
уравнение которой |
|||
|
получено |
при |
исключении |
переменной z |
из |
|
|
уравнений |
параболоида |
x2 + y2 = 2z |
и |
||
|
Рис. 2.4 |
плоскости z = 2 . |
x2 + y2 = ρ2 , |
|||
|
Введем цилиндрические координаты. Так как |
то |
21

|
уравнение |
параболоида |
примет вид z = |
ρ2 |
; |
уравнение плоскости при |
|||||||||||
|
2 |
||||||||||||||||
|
изменится . В области D |
||||||||||||||||
|
переходе |
к цилиндрическим |
координатам |
не |
|||||||||||||
|
0 ≤ϕ ≤ 2π , а 0 ≤ ρ ≤ 2 . Тогда, следуя формуле (2.8), имеем |
||||||||||||||||
|
2π |
2 |
2 |
||||||||||||||
|
∫∫∫(x2 + y2 )dxdydz =∫∫∫ρ2 ρdρdϕdz = ∫ dϕ∫ρ3dρ ∫dz = |
||||||||||||||||
|
V |
V |
0 |
0 |
ρ2 |
||||||||||||
|
2 |
2 |
|||||||||||||||
|
2π |
2 |
2π |
2 |
ρ5 |
||||||||||||
|
= ∫ dϕ∫ρ3dρ z |
2 = |
∫ |
dϕ∫ |
(2ρ3 − |
)dρ = |
|||||||||||
|
ρ |
2 |
|||||||||||||||
|
0 |
0 |
0 |
0 |
|||||||||||||
|
2 |
||||||||||||||||
|
2π |
ρ |
4 |
ρ |
6 |
2 |
2π |
(23 − |
2 |
4 |
8ϕ |
||||
|
= ∫ |
dϕ( |
− |
) |
= ∫ |
)dϕ = |
|||||||||
|
2 |
12 |
3 |
3 |
|||||||||||
|
0 |
0 |
0 |
||||||||||||
= 163π .
#
2.4. Вычисление объемов. С помощью тройных интегралов можно вычислить объем пространственной области, массу тела, занимающего область V , а также координаты центра тяжести этого тела и моменты инерции его относительно координатных осей и начала координат. Мы рассмотрим только геометрическое приложение тройного интеграла – вычисление объема пространственной области.
Как установлено в замечании 2.1 объем V пространственной области V может быть вычислен с помощью тройного интеграла по формуле
|
V = ∫∫∫dx dy dz. |
(2.9) |
||
|
V |
|||
|
В цилиндрической системе координат имеем |
|||
|
V = ∫∫∫ρ dρ dϕ dz. |
(2.10) |
||
|
V |
|||
|
Пример 2.4. Вычислить объем тела, ограниченного параболоидом |
|||
|
6 − x2 − y2 = z |
и конусом |
x2 + y2 = z2 |
|
|
(z ≥ 0) . |
|||
|
Решение. Тело (рис.2.5), объем которого |
|||
|
нужно найти, |
ограничено |
снизу конусом |
|
|
x2 + y2 = z2 , |
сверху – |
параболоидом |
|
|
6 − x2 − y2 = z |
и проектируетcя на плоскость |
||
|
xOy в область D , ограниченную окружностью |
Рис. 2.5 |
||
|
x2 + y2 = 4. Уравнение окружности получено |
в результате исключения z из уравнения конуса и параболоида.
22
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция и = f(x;y;z). Разбив область V сеткой поверхностей на п частей 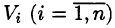 и выбрав в каждой из них произвольную точку
и выбрав в каждой из них произвольную точку 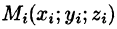 , составим интегральную сумму
, составим интегральную сумму 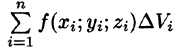 для функции
для функции 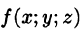 по области V (здесь
по области V (здесь 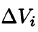 — объем элементарной области
— объем элементарной области 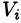 ).
).
Если предел интегральной суммы существует при неограниченном увеличении числа п таким образом, что каждая «элементарная область» 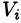 стягивается в точку (т. е. диаметр области
стягивается в точку (т. е. диаметр области 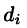 стремится к нулю, т.е.
стремится к нулю, т.е. 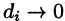 ), то его называют тройным интегралом от функции и = f(х;у;z) по области V и обозначают
), то его называют тройным интегралом от функции и = f(х;у;z) по области V и обозначают
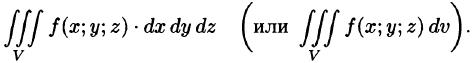
Таким образом, по определению, имеем:
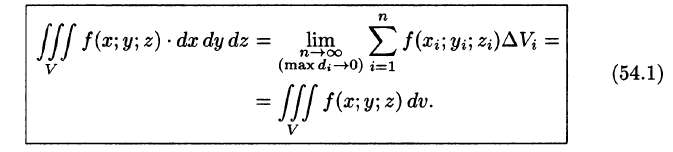
Здесь dv = dx dy dz — элемент объема.
Теорема:
Если функция и = f(x;y,z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (54.1) при 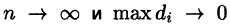 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек
существует и не зависит ни от способа разбиения области V на части, ни от выбора точек 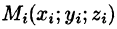 в них.
в них.
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
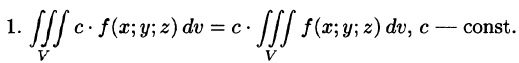
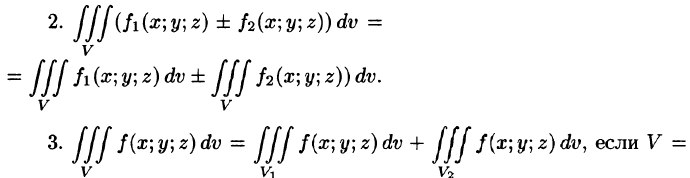
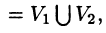
а пересечение 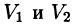 состоит из границы, их разделяющей.
состоит из границы, их разделяющей.
4. 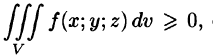 если в области V функция
если в области V функция 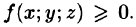
Если в области интегрирования 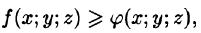 то и
то и
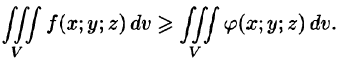
5.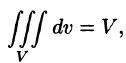 так как в случае
так как в случае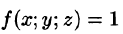 любая интегральная сумма имеет вид
любая интегральная сумма имеет вид 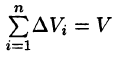 и численно равна объему тела.
и численно равна объему тела.
6. Оценка тройного интеграла:
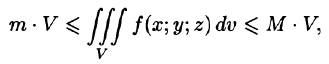
где m и М — соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.
7. Теорема о среднем значении: если функция f(x; у, z) непрерывна в замкнутой области V, то в этой области существует такая точка 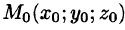 , что
, что
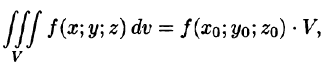
где V — объем тела.

Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
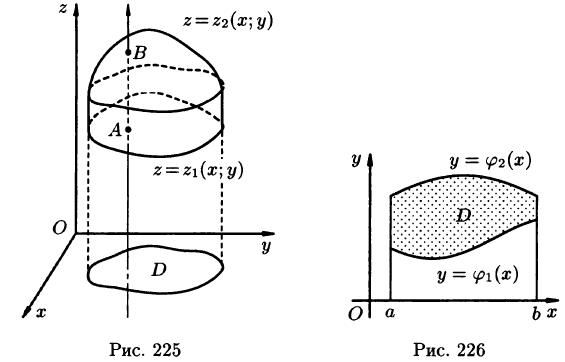
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью 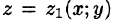 , сверху — поверхностью
, сверху — поверхностью 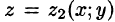 , причем
, причем 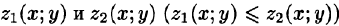 — непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху (см. рис. 225). Будем считать область V — правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции f(х; у, z) имеет место формула
— непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху (см. рис. 225). Будем считать область V — правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции f(х; у, z) имеет место формула
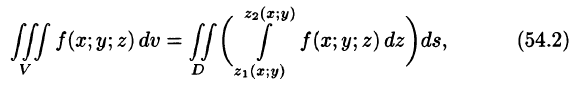
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). При этом сначала вычисляется внутренний интеграл по переменной г при постоянных х и у в пределах изменения z. Нижней границей интеграла является аппликата точки А — точки входа прямой, параллельной оси Oz в область V, т. е. 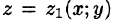 ; верхней границей — аппликата точки В — точки выхода прямой из области V, т. е.
; верхней границей — аппликата точки В — точки выхода прямой из области V, т. е. 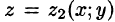 . Результат вычисления этого интеграла есть функция двух переменных: х и у.
. Результат вычисления этого интеграла есть функция двух переменных: х и у.
Если область D ограничена линиями 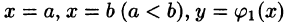 и
и 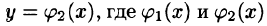 — непрерывные на отрезке [а, b] функции, причем
— непрерывные на отрезке [а, b] функции, причем 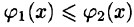 (см. рис. 226), то, переходя от двойного интеграла по области D к повторному, получаем формулу
(см. рис. 226), то, переходя от двойного интеграла по области D к повторному, получаем формулу
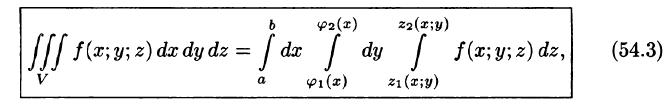
по которой вычисляется тройной интеграл в декартовых координатах.
Замечания:
- Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).
- Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.
Пример:
Вычислить
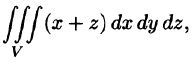
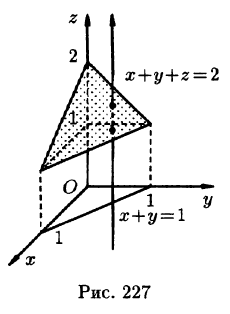
где V ограничена плоскостями х = 0, у =0, z = 1, x + y + z = 2 (рис. 227).
Решение:
Область V является правильной в направлении оси Oz (как, заметим, и в направлении осей Ох и Оу). Ее проекция на плоскость Оху является правильной в направлении оси Оу (и оси Ох). Согласно формуле (54.3), имеем:
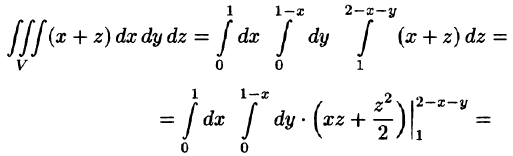
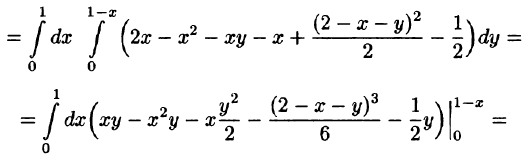
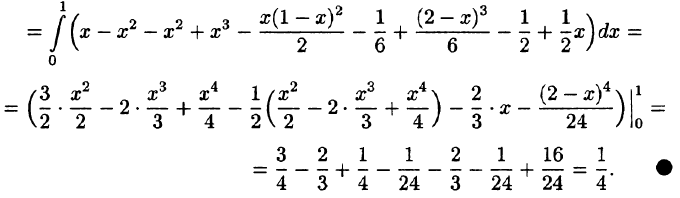
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.
Пусть совершена подстановка
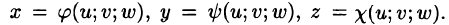
Если эти функции имеют в некоторой области 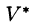 пространства Ouvw непрерывные частные производные и отличный от нуля определитель
пространства Ouvw непрерывные частные производные и отличный от нуля определитель
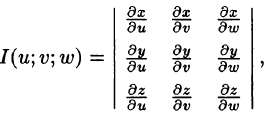
то справедлива формула замены переменных в тройном интеграле:
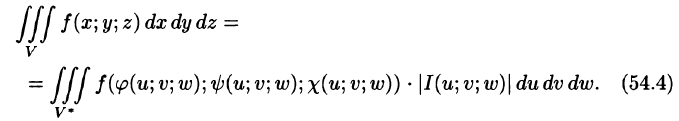
Здесь I(u; v;w) — определитель Якоби, или якобиан преобразования (примем без доказательства).
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.
Положение точки М(х; у; z) в пространстве Oxyz можно определить заданием трех чисел 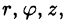 где r — длина радиуса-вектора проекции точки М на плоскость Оху,
где r — длина радиуса-вектора проекции точки М на плоскость Оху, 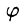 — угол, образованный этим радиусом-вектором с осью Ox, z — аппликата точки М (см. рис. 228).
— угол, образованный этим радиусом-вектором с осью Ox, z — аппликата точки М (см. рис. 228).
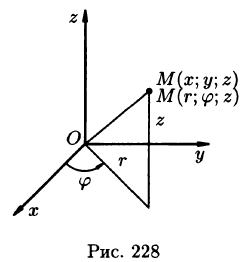
Эти три числа (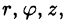 ) называются цилиндрическими координатами точки М.
) называются цилиндрическими координатами точки М.
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
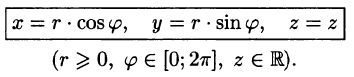
Возьмем в качестве и, v, w цилиндрические координаты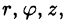 и вычислим якобиан преобразования:
и вычислим якобиан преобразования:
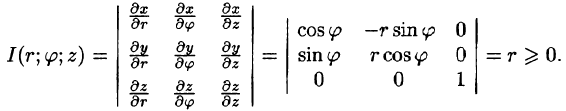
Формула замены переменных (54.4) принимает вид
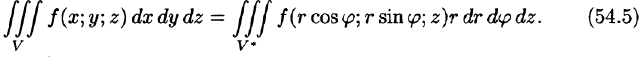
Таким образом, вычисление тройного интеграла приводится к интегрированию по r, по 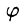 и по z аналогично тому, как это делается в декартовых координатах.
и по z аналогично тому, как это делается в декартовых координатах.
Замечание:
К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.
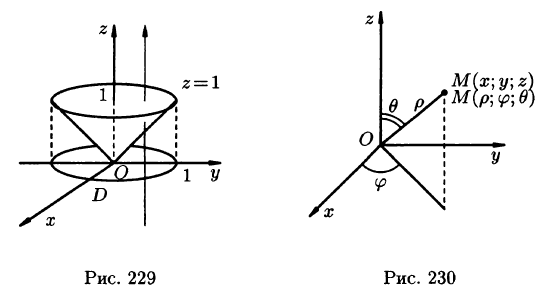
Пример:
Вычислить 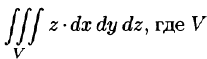 — область, ограниченная верхней частью конуса
— область, ограниченная верхней частью конуса 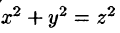 и плоскостью z = 1.
и плоскостью z = 1.
Решение:
На рис. 229 изображена область интегрирования V. Вычислим интеграл путем перехода к цилиндрическим координатам: 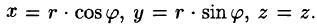 Здесь
Здесь 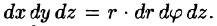 Уравнение конуса примет вид
Уравнение конуса примет вид 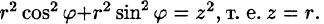 Уравнение окружности
Уравнение окружности 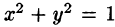 (границы области D) запишется так: r= 1. Новые переменные изменяются в следующих пределах: r— от 0 до 1,
(границы области D) запишется так: r= 1. Новые переменные изменяются в следующих пределах: r— от 0 до 1,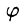 — от 0 до
— от 0 до 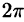 , a z — от r до 1 (прямая, параллельная оси Oz, пересекающая область D, входит в конус z =r и выходит из него на высоте z = 1).
, a z — от r до 1 (прямая, параллельная оси Oz, пересекающая область D, входит в конус z =r и выходит из него на высоте z = 1).
Таким образом, согласно формуле (54.5), получаем:
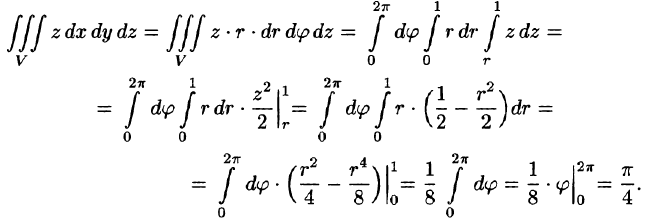
Заметим, что, не переходя к цилиндрическим координатам, получим:
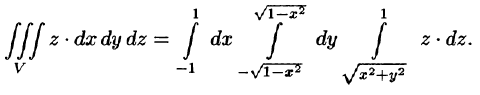
Сферическими координатами точки М(х; у; z) пространства Oxyz называется тройка чисел 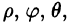 где р — длина радиуса-вектора точки
где р — длина радиуса-вектора точки 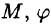 — угол, образованный проекцией радиуса-вектора
— угол, образованный проекцией радиуса-вектора 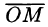 на плоскость Оху и осью Ох, в — угол отклонения радиуса-вектора
на плоскость Оху и осью Ох, в — угол отклонения радиуса-вектора 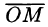 от оси Oz (см. рис. 230).
от оси Oz (см. рис. 230).
Сферические координаты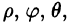 связаны с декартовыми координатами х, у, z соотношениями:
связаны с декартовыми координатами х, у, z соотношениями:
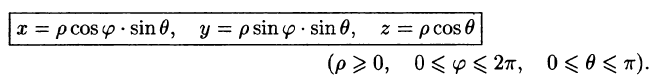
В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования
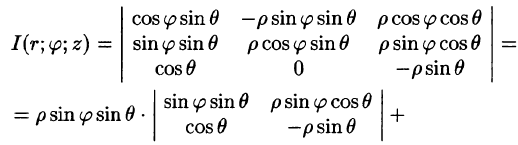
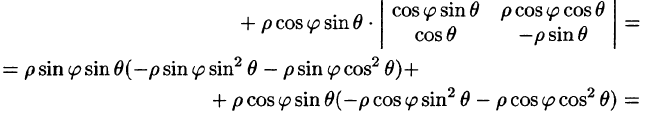
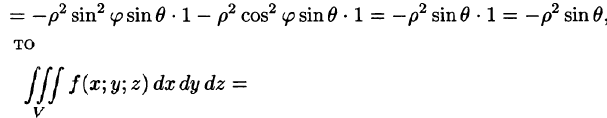
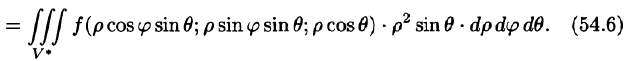
Замечание:
Переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравнение его границы 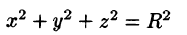 в сферических координатах имеет вид р = R) или его часть, а также если подынтегральная функция имеет вид
в сферических координатах имеет вид р = R) или его часть, а также если подынтегральная функция имеет вид 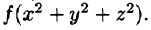
Пример 54.3. Вычислить
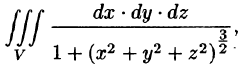
где V — шар 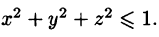
Решение:
Вычислим интеграл путем перехода к сферическим координатам: 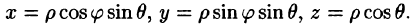 Тогда
Тогда
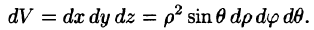
Граница области V — сфера и ее уравнение имеет вид р = 1, подынтегральная функция после замены переменных примет вид 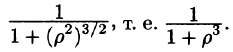 Новые переменные изменяются в следующих пределах: р —от 0 до 1, у — от 0 до
Новые переменные изменяются в следующих пределах: р —от 0 до 1, у — от 0 до 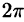 ,
, 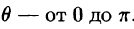 Таким образом, согласно формуле (54.6),
Таким образом, согласно формуле (54.6),
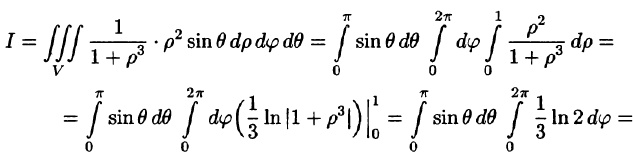
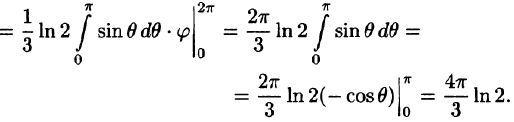
Некоторые приложения тройного интеграла Объем тела
Объем области V выражается формулой 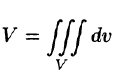 или
или 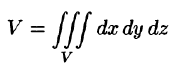 — в декартовых координатах,
— в декартовых координатах,

Масса тела
Масса тела m при заданной объемной плотности 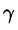 вычисляется с помощью тройного интеграла как
вычисляется с помощью тройного интеграла как
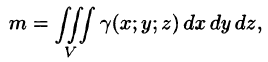
где 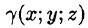 — объемная плотность распределения массы в точке M{x;y;z).
— объемная плотность распределения массы в точке M{x;y;z).
Статические моменты
Моменты 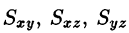 тела относительно координатных плоскостей Оху, Oxz, Oyz вычисляются по формулам
тела относительно координатных плоскостей Оху, Oxz, Oyz вычисляются по формулам
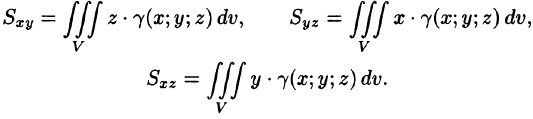
Центр тяжести тела
Координаты центра тяжести тела V находятся по формулам
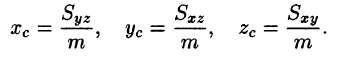
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
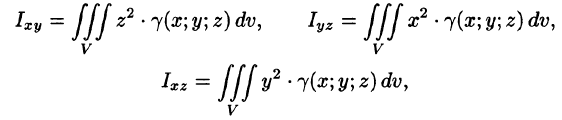
а моменты инерции относительно координатных осей:
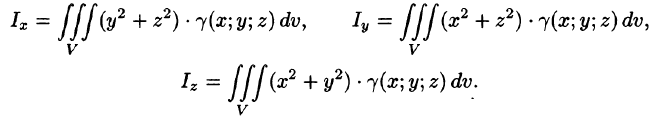
Пример:
Найти объем тела, ограниченного поверхностями
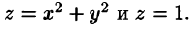
Решение:
Данное тело ограничено сверху плоскостью z = 1, снизу — параболоидом 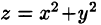 (см. рис. 231). Объем тела находим, используя цилиндрические координаты:
(см. рис. 231). Объем тела находим, используя цилиндрические координаты:
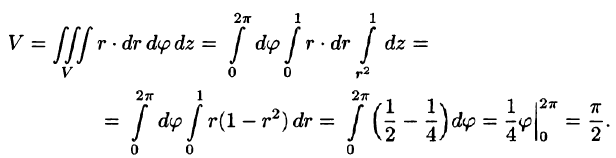
Пример:
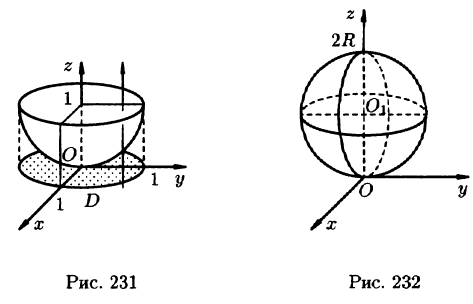
Найти массу шара 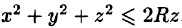 , если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
Решение:
Уравнение сферы 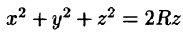 можно записать так:
можно записать так: 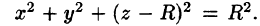 Центр шара расположен в точке
Центр шара расположен в точке 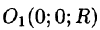 (см. рис. 232). Пусть M(x;y;z) — произвольная точка шара. Тогда, по условию, плотность
(см. рис. 232). Пусть M(x;y;z) — произвольная точка шара. Тогда, по условию, плотность 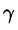 определяется формулой
определяется формулой
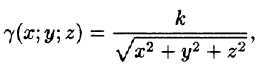
где k — коэффициент пропорциональности, 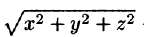 — расстояние от точки М до начала координат.
— расстояние от точки М до начала координат.
Итак,
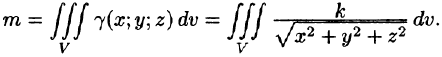
Вычислять интеграл будем в сферических координатах. Уравнение сферы 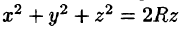 примет вид
примет вид 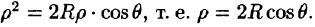
Поэтому сферические координаты будут изменяться в следующих пределах:
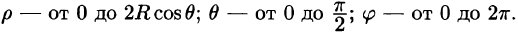
Подынтегральная функция примет вид 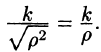 Поэтому
Поэтому
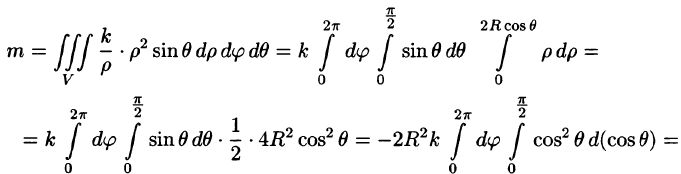
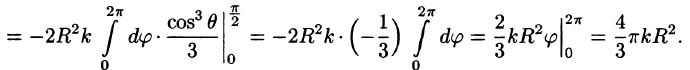
Из соображений симметрии следует, что 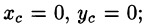 вычислив интеграл
вычислив интеграл 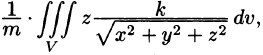 найдем
найдем 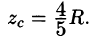 Итак, координаты центра тяжести
Итак, координаты центра тяжести 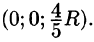
Тройной интеграл


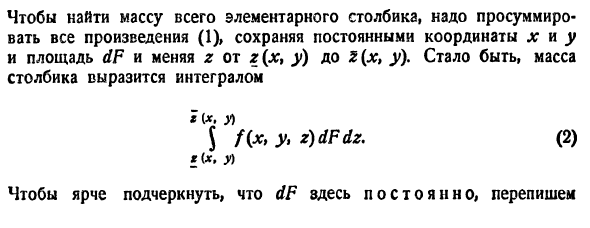

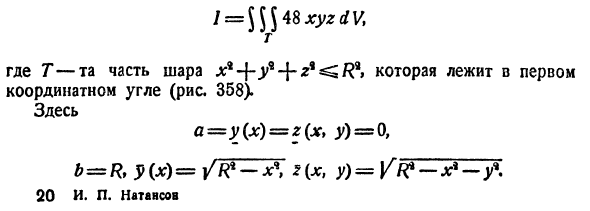

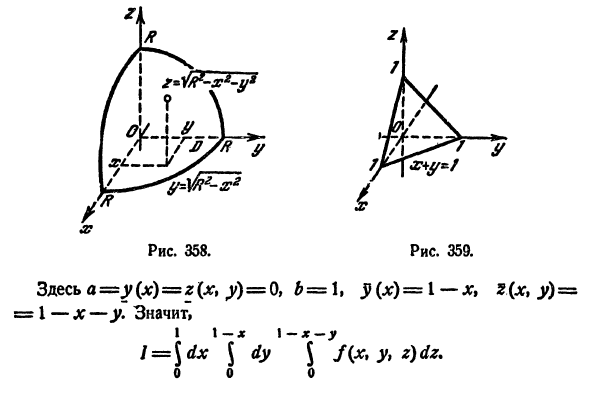











Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Примеры решений тройных интегралов
В этом разделе вы найдете подробные решения, связанные и вычислением и применением тройных интегралов: от непосредственного вычисления (в декартовых, цилиндрических, сферических координатах), до применения к нахождению объемов тел, массы, моментов и т.п. Примеры сгруппированы по темам:
Спасибо за ваши закладки и рекомендации
Тройные интегралы: примеры решений
Задача 1. Вычислить тройной интеграл
$$iiint_V x^2yz dx dy dz, quad V: -1 le x le 2, 0le y le 3, 2 le z le 3. $$
Задача 2. Переходя к сферическим координатам, вычислить интеграл
$$iiint_V x^2 dxdydz, quad V: x^2+y^2+z^2=R^2,, zge 0, xgt 0.$$
Задача 3. Переходя к цилиндрическим координатам вычислить интеграл
$$iiint_V x^2 dxdydz, quad V: x^2+y^2=x,, z=x^2+y^2, z=0.$$
Задача 4. Решить тройной интеграл двумя способами (цилидрическая и сферическая замена координат)
$$iiint_G(x^2+y^2+z^2)^2 dxdydz,quad G={(x,y,z):x^2+y^2+z^2le a^2,x+zge0}$$
Трудности с задачами? МатБюро поможет с интегралами.
Объемы тел: примеры решений
Задача 5. Найти объем тела, заданного ограничивающими его поверхностями (внутри цилиндра).
$$z=sqrt{100-x^2-y^2},, z=6,, x^2+y^2=51$$
Задача 6. Найти объем тела, ограниченного поверхностями
$$x^2+y^2=9x, x^2+y^2=12x, z=sqrt{x^2+y^2}, z=0, y ge 0.$$
Задача 7. Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями:
$$z=2-x, z=0, y=sqrt{x}, y=frac{1}{4}x^2.$$
Задача 8. Найти объем тела, ограниченного координатными плоскостями и поверхностью
$$
left(frac{x}{a}+ frac{y}{b} + frac{z}{c} right)^3 = sin left(pi frac{frac{x}{a}+ frac{y}{b}}{frac{x}{a}+ frac{y}{b} + frac{z}{c} } right)
$$
Задача 9. Найти объем тела, ограниченного поверхностью $x^2+y^2+z^2=2x+3y$.
Моменты, масса тела: примеры решений
Задача 10. Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью
$$(x^2+y^2+z^2 )^3=frac{x^2+y^2}{z^2} $$
с плотностью $z=0$ $(z ge 0)$.
Задача 11. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости $xOy$, а ось симметрии совпадает с осью $Oz$, если заданы радиус основания $R$, высота цилиндра $H$ и функция плотности $gamma(rho)$, где $rho$ – полярный радиус точки.
$$ R=2, H=0,5, gamma=2+rho^2+rho^3.$$
Задача 12. Найти массу тела, заданного системой неравенств, если плотность тела в каждой точке задана функцией $mu$.
$$ frac{1}{2}sqrt{x^2+y^2} le z le sqrt{4-x^2-y^2}, quad mu =frac{5}{8}z. $$
Задача 13. Найти момент инерции относительно оси Oz тела, ограниченного заданными поверхностями.
$$z=-x^2-y^2, z=x^2+y^2-8$$
Не берется интеграл? Вычислим быстро и подробно поясним!
Полезные ссылки
- Интегралы – примеры решений
- Применение интегралов – примеры решений
- Двойные интегралы – примеры решений
- Криволинейные интегралы – примеры решений
- Поверхностные интегралы – примеры решений
- Учебник с примерами онлайн по тройным интегралам
