Как найти объем цилиндра через боковую площадь

Как посчитать объем цилиндра

Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Зная радиус r и высоту h

Зная диаметр d и высоту h

Зная площадь основания S_o и высоту h

Зная площадь боковой поверхности S_b и высоту h

См. также

Цилиндр является одной из распространенных форм пространственных тел, с которыми мы сталкиваемся ежедневно. Действительно, кружка, таблетка, дымоход, труба и другие предметы имеют цилиндрическую форму. В данной статье рассмотрим вопрос, как рассчитать объем цилиндра, используя различные известные параметры этой фигуры.

Определение цилиндра в геометрии

Прежде чем переходить к ответу на вопрос, как рассчитать объем цилиндра, разберемся, с какой фигурой мы имеем дело.

С геометрической точки зрения цилиндр образован двумя одномерными элементами. Первый – это кривая, которая является направляющей. Второй – это прямой отрезок, который называется образующей. Когда отрезок не находится в плоскости кривой, если его один конец соединить с кривой и перемещать параллельно самому себе вдоль нее, то мы получим цилиндрическую поверхность.

Под предоставленное определение подходит множество пространственных фигур, включая гиперболические, параболические и эллиптические цилиндры. Тем не менее в данной статье будем рассматривать только круглый прямой цилиндр. Круглым он называется по причине того, что его основания являются кругами (направляющая – окружность), а прямой он потому, что отрезок образующей перпендикулярен основаниям. Для наглядности описанный цилиндр показан на рисунке.

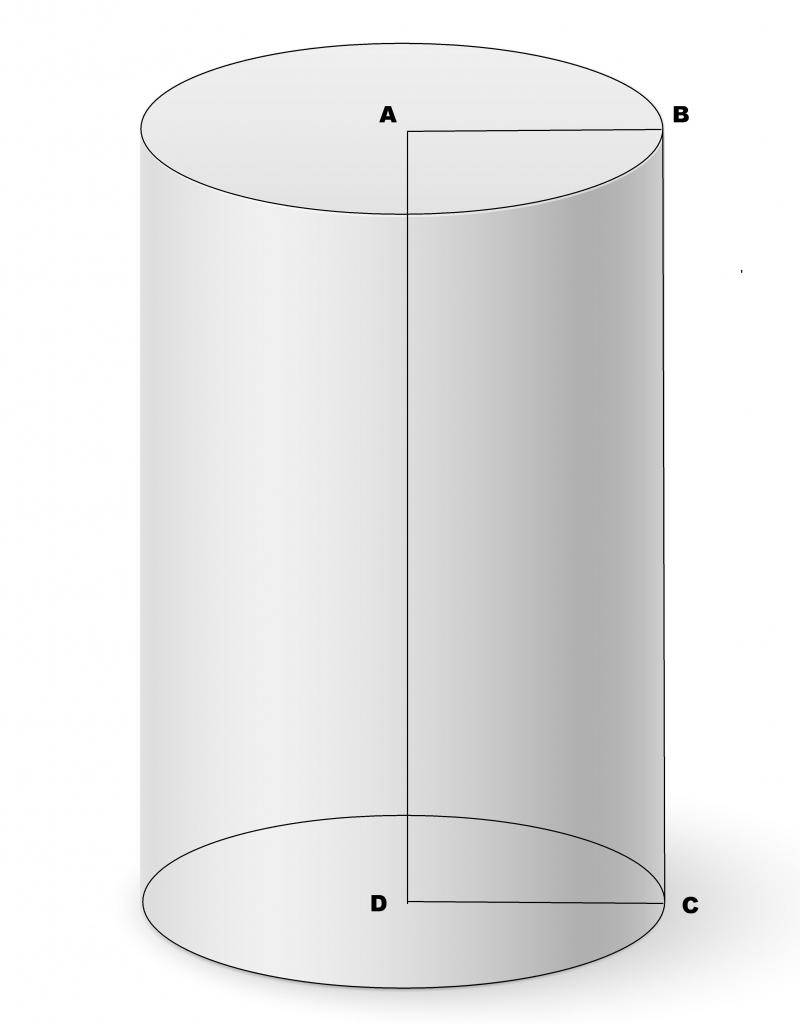
Как рассчитать объем цилиндра через радиус (диаметр) и высоту?

Ответом на этот вопрос является стандартная формула, которая справедлива для любого цилиндра и даже призмы. Запишем ее:

V = S_o * h

Поскольку в рассматриваемом случае основание – это правильный круг, то можно конкретизировать это выражение и переписать его в следующем виде:

V = pi * r² * h

Если известен диаметр, то найти объем цилиндра можно, используя такое выражение:

V = pi / 4 * d² * h

Определение объема цилиндра через площадь боковой поверхности

Еще одним способом рассчитать объем цилиндра, является использование площади его боковой поверхности. Этой поверхностью называется совокупность точек всех образующих, которые соединяют два основания фигуры. Боковая поверхность имеет цилиндрическую форму. Если ее разрезать вдоль одной из образующих и раскрыть, то получится развертка фигуры, показанная ниже.

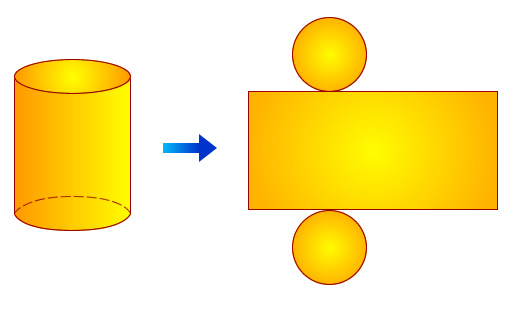
Видно, что в развернутом виде боковая поверхность является обычным прямоугольником, стороны которого равны высоте и длине окружности основания. Последний факт позволяет записать формулу для площади S_b этой фигуры:

S_b = 2 * pi * r * h

Если известен радиус r фигуры, тогда высота ее будет равна:

h = S_b / (2 * pi * r)

Тогда для объема V формула для цилиндра запишется в виде:

V = r * S_b / 2

Если же известна площадь S_b и высота h, тогда радиус фигуры будет равен:

r = S_b / (2 * pi * h)

Подставляя его в выражение для объема, приходим к следующей формуле:

V = S_b² / (4 * pi * h)

Можно заметить, что обе формулы с использованием боковой площади S_b соответствуют размерности объема (м³).

Важно понимать, что объем круглого прямого цилиндра можно определить только в том случае, если известны какие-нибудь два его параметра.

Задача на расчет объема цилиндра через площадь его полной поверхности

Предположим, что цилиндр имеет высоту 21 см, а площадь его развертки составляет 335 см². Необходимо определить объем фигуры.

Ни одна из приведенных выше формул не способна дать нам искомый ответ. В таком случае, как рассчитать объем цилиндра? Как выше было сказано, достаточно знать любые два параметра фигуры, чтобы определить величину V. В данном случае запишем сначала формулу для общей площади цилиндра:

S = S_b + 2 * S_o = 2 * pi * r * h + 2 * pi * r²

Подставим в это равенство известные данные, получим:

r² + 21 * r – 53,34 = 0

После подстановки данных мы разделили левую и правую части на 2 * pi и перенесли все члены в одну часть равенства.

Таким образом, перед нами стоит задача решения квадратного уравнения. Используем стандартный метод решения через дискриминант, имеем:

дискриминант D = 654,36;

r = 2,29 см.

При решении уравнения мы отбросили отрицательный корень.

Теперь для определения объема цилиндра можно воспользоваться формулой с параметрами r и h. Подставляя их в указанную формулу, приходим к ответу на задачу: V = 345,8 см³.

Цилиндр является одной из распространенных форм пространственных тел, с которыми мы сталкиваемся ежедневно. Действительно, кружка, таблетка, дымоход, труба и другие предметы имеют цилиндрическую форму. В данной статье рассмотрим вопрос, как рассчитать объем цилиндра, используя различные известные параметры этой фигуры.

Определение цилиндра в геометрии

Прежде чем переходить к ответу на вопрос, как рассчитать объем цилиндра, разберемся, с какой фигурой мы имеем дело.

Вам будет интересно:Что такое глобальные проблемы человечества?

С геометрической точки зрения цилиндр образован двумя одномерными элементами. Первый – это кривая, которая является направляющей. Второй – это прямой отрезок, который называется образующей. Когда отрезок не находится в плоскости кривой, если его один конец соединить с кривой и перемещать параллельно самому себе вдоль нее, то мы получим цилиндрическую поверхность.

Под предоставленное определение подходит множество пространственных фигур, включая гиперболические, параболические и эллиптические цилиндры. Тем не менее в данной статье будем рассматривать только круглый прямой цилиндр. Круглым он называется по причине того, что его основания являются кругами (направляющая – окружность), а прямой он потому, что отрезок образующей перпендикулярен основаниям. Для наглядности описанный цилиндр показан на рисунке.

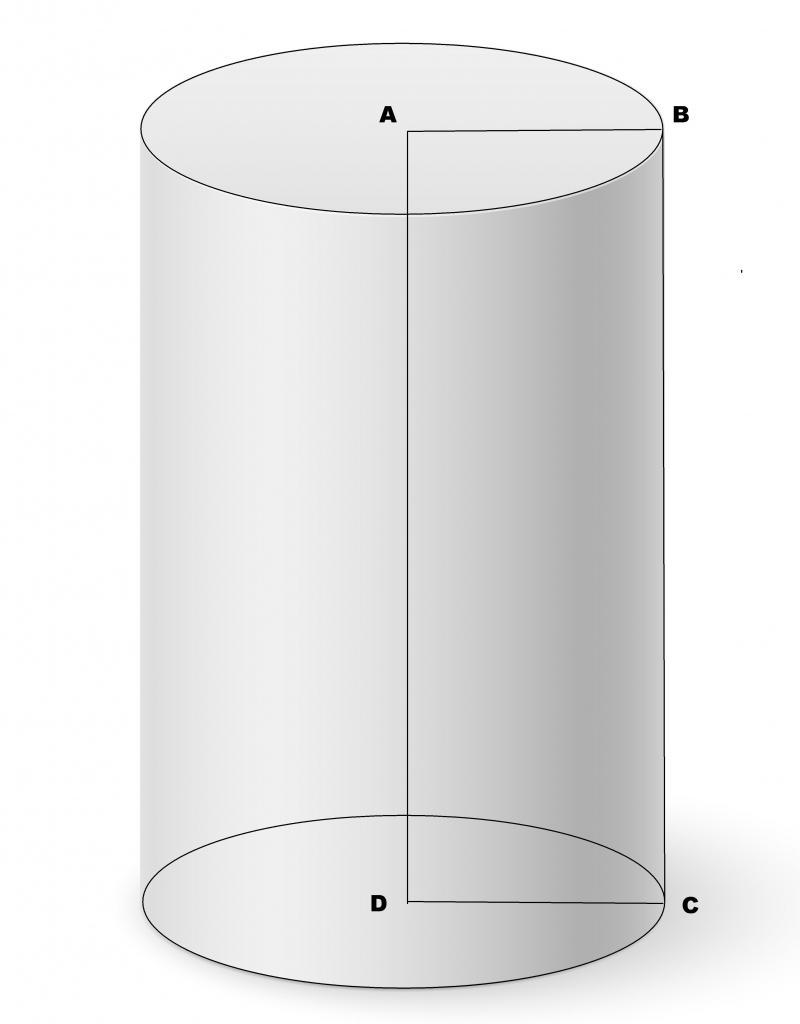
Как рассчитать объем цилиндра через радиус (диаметр) и высоту?

Ответом на этот вопрос является стандартная формула, которая справедлива для любого цилиндра и даже призмы. Запишем ее:

V = So * h

Поскольку в рассматриваемом случае основание – это правильный круг, то можно конкретизировать это выражение и переписать его в следующем виде:

V = pi * r2 * h

Если известен диаметр, то найти объем цилиндра можно, используя такое выражение:

V = pi / 4 * d2 * h

Определение объема цилиндра через площадь боковой поверхности

Еще одним способом рассчитать объем цилиндра, является использование площади его боковой поверхности. Этой поверхностью называется совокупность точек всех образующих, которые соединяют два основания фигуры. Боковая поверхность имеет цилиндрическую форму. Если ее разрезать вдоль одной из образующих и раскрыть, то получится развертка фигуры, показанная ниже.

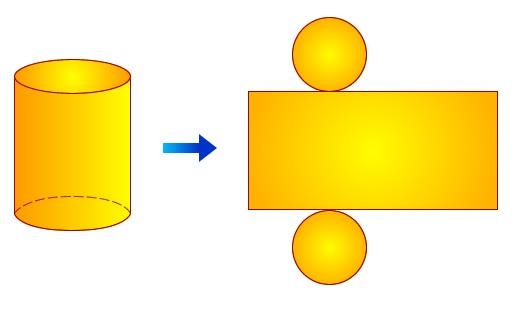
Видно, что в развернутом виде боковая поверхность является обычным прямоугольником, стороны которого равны высоте и длине окружности основания. Последний факт позволяет записать формулу для площади Sb этой фигуры:

Sb = 2 * pi * r * h

Если известен радиус r фигуры, тогда высота ее будет равна:

h = Sb / (2 * pi * r)

Тогда для объема V формула для цилиндра запишется в виде:

V = r * Sb / 2

Если же известна площадь Sb и высота h, тогда радиус фигуры будет равен:

r = Sb / (2 * pi * h)

Подставляя его в выражение для объема, приходим к следующей формуле:

V = Sb2 / (4 * pi * h)

Можно заметить, что обе формулы с использованием боковой площади Sb соответствуют размерности объема (м3).

Важно понимать, что объем круглого прямого цилиндра можно определить только в том случае, если известны какие-нибудь два его параметра.

Задача на расчет объема цилиндра через площадь его полной поверхности

Предположим, что цилиндр имеет высоту 21 см, а площадь его развертки составляет 335 см2. Необходимо определить объем фигуры.

Ни одна из приведенных выше формул не способна дать нам искомый ответ. В таком случае, как рассчитать объем цилиндра? Как выше было сказано, достаточно знать любые два параметра фигуры, чтобы определить величину V. В данном случае запишем сначала формулу для общей площади цилиндра:

S = Sb + 2 * So = 2 * pi * r * h + 2 * pi * r2

Подставим в это равенство известные данные, получим:

r2 + 21 * r – 53,34 = 0

После подстановки данных мы разделили левую и правую части на 2 * pi и перенесли все члены в одну часть равенства.

Таким образом, перед нами стоит задача решения квадратного уравнения. Используем стандартный метод решения через дискриминант, имеем:

дискриминант D = 654,36;

r = 2,29 см.

При решении уравнения мы отбросили отрицательный корень.

Теперь для определения объема цилиндра можно воспользоваться формулой с параметрами r и h. Подставляя их в указанную формулу, приходим к ответу на задачу: V = 345,8 см3.

Жду ваши вопросы и мнения в комментариях

Площадь полной поверхности цилиндра равна:

Онлайн калькулятор для цилиндра позволяет по известным данным вычислить:

• объем цилиндра,
• площадь основания, площадь боковой поверхности и  площадь полной поверхности цилиндра,
• элементы: радиус, диаметр и высоту.

Калькулятор для цилиндра: комментарий

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Обозначения для цилиндра:
R – радиус, D – диаметр,
V – объем,
Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,
h – высота прямого кругового цилиндра (h1 и h2 — минимальная  и максимальная высота)
π – число Пи которое всегда примерно равно 3,14.

Прямой круговой цилиндр

Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.

Формулы для прямого кругового цилиндра:

Найти объем цилиндра, если известны:

• радиус и высота цилиндра: V=πR²h
• диаметр и высота цилиндра: V=πD²/4h
• площадь и высота цилиндра: V=Sоh

Площадь(Sб) боковой поверхности прямого кругового цилиндра

Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h

Площадь(Sо) основания цилиндра

Основание цилиндра —круг, поэтому площадь одного основания находится по формуле площади круга: Sо=πR².

Площадь(S)  полной поверхности прямого кругового цилиндра

Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR²=2πR(h+R)

Формулы нахождения радиуса и диаметра по:

• высоте и объему: R=√(V/πh), D=2*√(V/πh)
• площади боковой поверхности и высоте: R=Sб/2πh, D=2*Sб/2πh
• площади основания и высоте: R=√(Sо/π), R=2*√(Sо/π)

Формулы нахождения высоты по:

• радиусу и объему: h=V/πR²
• площади боковой поверхности и радиусу: h=Sб/2πR
• площади полной поверхности и радиусу: h=S/2πR-R

Скошенный цилиндр

Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h1 и максимальной высотой h2.

Формулы для скошенного цилиндра:

• Объем скошенного цилиндра: V=πR²(h1+h2)²
• Площадь(Sб) боковой поверхности скошенного цилиндра: Sб=πR(h1+h2)
• Площадь(Sо) оснований скошенного цилиндра: Sо=πR²+πR √(R2+((h1−h2)/2)²)
• Площадь(S) полной поверхности скошенного цилиндра  
  S=Sб+Sо= πR(h1+h2)+ πR²+πR √ (R²+((h1−h2)/2)²)  = πR[(h1+h2)+ R+√ (R²+((h1−h2)/2)²) ]

Список всех онлайн-конвертеров на странице «Калькуляторы«.