Содержание:
Цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через его сторону (рис. 26). На рисунке 27 показано образование цилиндра при вращении прямоугольника 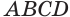
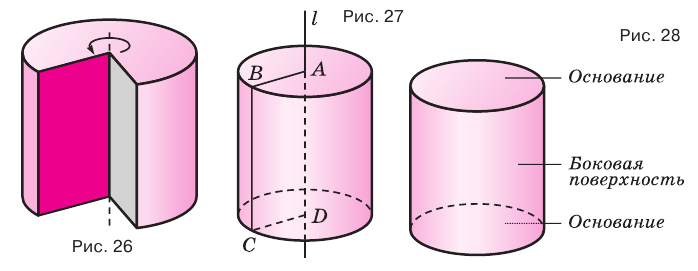
Образующая цилиндра является его высотой.
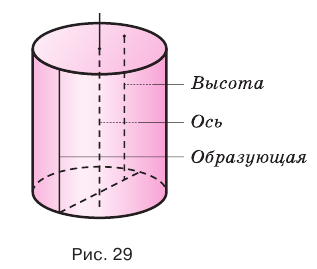
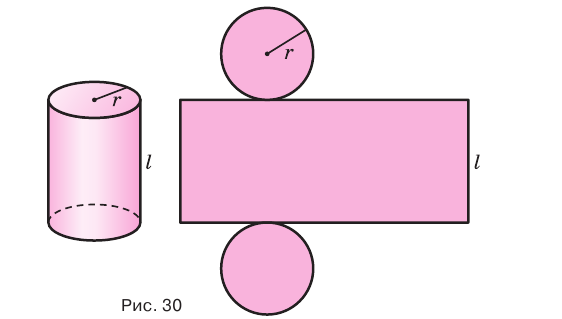
Поверхность цилиндра можно развернуть на плоскость, в результате получится прямоугольник, представляющий боковую поверхность цилиндра, и два круга, представляющих его основания. На рисунке 30 показан цилиндр и его развертка.
Теорема 4.
Боковая поверхность цилиндра равна произведению длины окружности основания и образующей:
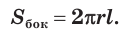
На плоскости важной конфигурацией, которая часто встречается в задачах, является сочетание окружности с прямой. Подобной пространственной конфигурацией является сочетание цилиндра с плоскостью.
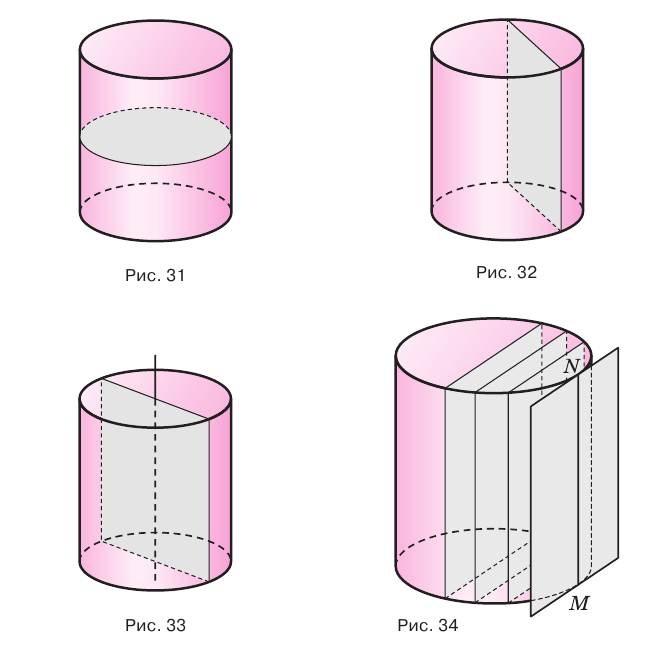
Если цилиндр пересечь плоскостью, параллельной основанию, то получится круг, равный основанию (рис. 31), а если плоскостью, перпендикулярной основанию, то — прямоугольник, одна сторона которого равна высоте цилиндра (рис. 32). Осевое сечение цилиндра, т. е. сечение плоскостью, проходящей через ось цилиндра, является прямоугольником, стороны которого равны высоте цилиндра и диаметру его основания (рис. 33).
Будем двигать плоскость, проходящую через ось цилиндра, параллельно самой себе (рис. 34). При этом две противолежащие стороны прямоугольника-сечения цилиндра, являющиеся хордами оснований, будут уменьшаться, а две другие стороны, которые являются образующими цилиндра, — сближаться до того момента, пока не совпадут. Получим плоскость, содержащую образующую 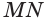 цилиндра и не имеющую с ним других общих точек. Такая плоскость называется касательной плоскостью цилиндра. Любая прямая, проведенная в касательной плоскости цилиндра и отличная от образующей, имеет с цилиндром единственную общую точку. Такая прямая называется касательной прямой цилиндра.
цилиндра и не имеющую с ним других общих точек. Такая плоскость называется касательной плоскостью цилиндра. Любая прямая, проведенная в касательной плоскости цилиндра и отличная от образующей, имеет с цилиндром единственную общую точку. Такая прямая называется касательной прямой цилиндра.
Теорема 5.
Если плоскость касается цилиндра по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 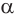 касается цилиндра с осью
касается цилиндра с осью 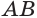 по образующей
по образующей 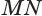 (рис. 35). Докажем, что плоскость, содержащая образующую
(рис. 35). Докажем, что плоскость, содержащая образующую 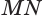 и ось
и ось 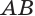 , перпендикулярна плоскости
, перпендикулярна плоскости  .
.
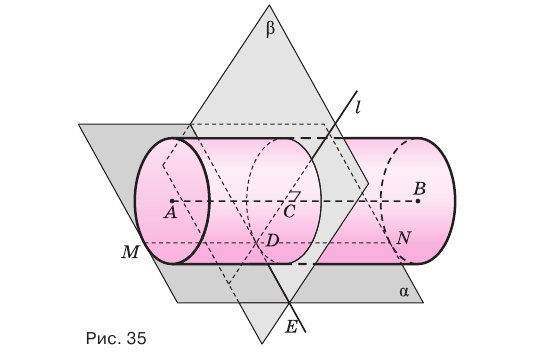
Проведем прямую 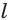 , которая пересекает прямую
, которая пересекает прямую 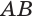 в точке
в точке 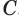 , прямую
, прямую 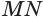 в точке
в точке 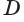 и перпендикулярна оси
и перпендикулярна оси 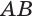 . Через точку
. Через точку 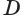 проведем плоскость
проведем плоскость 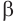 , перпендикулярную образующей
, перпендикулярную образующей 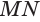 . Эта плоскость пересекает цилиндр по кругу, центр которого находится в точке
. Эта плоскость пересекает цилиндр по кругу, центр которого находится в точке 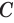 , а плоскость
, а плоскость 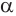 — по прямой
— по прямой 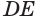 , касающейся окружности с центром
, касающейся окружности с центром 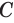 . Учитывая свойство касательной к окружности, можем утверждать, что прямая
. Учитывая свойство касательной к окружности, можем утверждать, что прямая 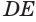 перпендикулярна радиусу
перпендикулярна радиусу 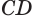 окружности с центром в точке
окружности с центром в точке 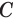 . Кроме того, поскольку прямая
. Кроме того, поскольку прямая 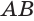 параллельна прямой
параллельна прямой 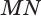 , то прямая
, то прямая 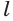 перпендикулярна прямой
перпендикулярна прямой 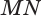 . Получили, что прямая
. Получили, что прямая 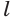 перпендикулярна как прямой
перпендикулярна как прямой 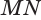 , так и прямой
, так и прямой 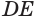 , которые пересекаются и лежат в плоскости
, которые пересекаются и лежат в плоскости 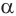 . Поэтому по признаку перпендикулярности прямой и плоскости прямая
. Поэтому по признаку перпендикулярности прямой и плоскости прямая 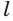 перпендикулярна плоскости
перпендикулярна плоскости 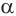 . Но плоскость, содержащая образующую
. Но плоскость, содержащая образующую 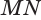 и ось
и ось 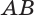 , проходит и через прямую
, проходит и через прямую 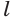 . Поэтому она, по признаку перпендикулярности плоскостей, перпендикулярна плоскости
. Поэтому она, по признаку перпендикулярности плоскостей, перпендикулярна плоскости 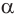 .
.
Теорема 5 выражает свойство касательной плоскости цилиндра.
Теорема 6.
Плоскость касается цилиндра, если она проходит через его образующую и перпендикулярна плоскости, содержащей эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 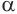 содержит образующую
содержит образующую 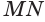 цилиндра и перпендикулярна плоскости, проходящей через эту образующую и ось
цилиндра и перпендикулярна плоскости, проходящей через эту образующую и ось 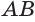 (рис. 36). Докажем, что плоскость
(рис. 36). Докажем, что плоскость 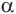 не имеет с цилиндром других общих точек, кроме точек образующей
не имеет с цилиндром других общих точек, кроме точек образующей 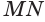 .
.
Пусть 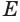 — точка плоскости
— точка плоскости 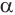 , не принадлежащая образующей
, не принадлежащая образующей 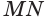 . Через эту точку проведем плоскость
. Через эту точку проведем плоскость 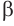 , перпендикулярную оси
, перпендикулярную оси 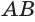 . Она пересечет цилиндр по кругу с центром
. Она пересечет цилиндр по кругу с центром 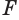 , образующую
, образующую 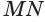 в некоторой точке
в некоторой точке 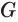 и плоскость
и плоскость 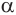 по прямой
по прямой 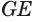 . Поскольку плоскости
. Поскольку плоскости 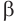 и
и 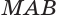 обе перпендикулярны плоскости
обе перпендикулярны плоскости 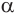 , то их линия пересечения
, то их линия пересечения 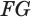 также перпендикулярна плоскости
также перпендикулярна плоскости 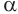 , а потому
, а потому 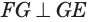 . Учитывая, что
. Учитывая, что 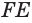 и
и 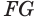 — соответственно гипотенуза и катет прямоугольного треугольника
— соответственно гипотенуза и катет прямоугольного треугольника 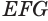 , получим, что
, получим, что 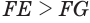 . Значит, точка
. Значит, точка 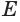 не принадлежит цилиндру с осью
не принадлежит цилиндру с осью 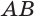 .
.
Теорема 6 выражает признак касательной плоскости цилиндра.
Пусть имеется цилиндр (рис. 37). Впишем в одно из оснований цилиндра многоугольник 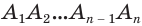 , через его вершины
, через его вершины 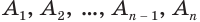 проведем образующие
проведем образующие 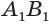 ,
, 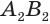 , …,
, …, 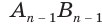 ,
, 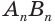 и соединим их другие концы
и соединим их другие концы 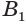 ,
, 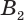 , …,
, …, 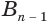 ,
, 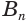 . В результате получим призму
. В результате получим призму 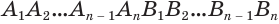 . Ее называют призмой, вписанной в цилиндр, а сам цилиндр называют цилиндром, описанным около призмы.
. Ее называют призмой, вписанной в цилиндр, а сам цилиндр называют цилиндром, описанным около призмы.
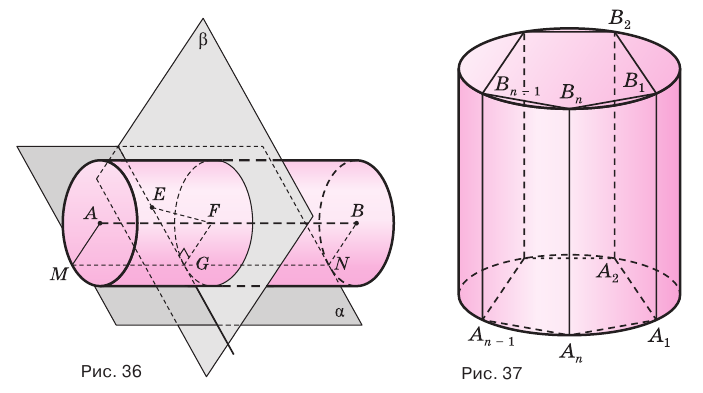
Если цилиндр описан около призмы, то основания цилиндра описаны около оснований призмы, а боковая поверхность цилиндра содержит боковые ребра призмы.
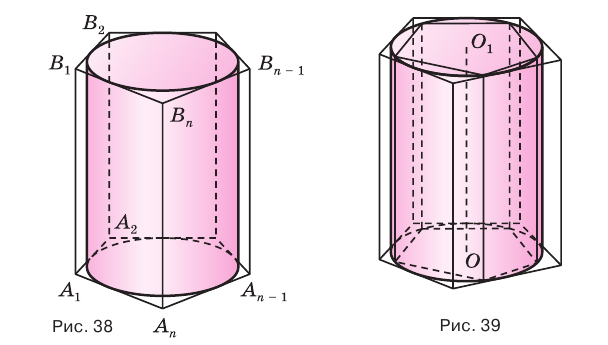
Подобным образом вводится понятие призмы, описанной около цилиндра, и цилиндра, вписанного в призму (рис. 38). Если призма описана около цилиндра, то ее основания описаны около оснований цилиндра, а боковые грани касаются боковой поверхности цилиндра.
Теорема 7.
Объем цилиндра равен произведению площади его основания и образующей:
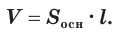
Доказательство:
Пусть имеется цилиндр с осью 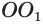 (рис. 39). В него впишем правильную призму
(рис. 39). В него впишем правильную призму 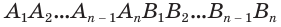 и, кроме того, около него опишем правильную призму
и, кроме того, около него опишем правильную призму 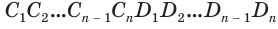 . В соответствии с теоремой 3 объем первой призмы равен произведению площади многоугольника
. В соответствии с теоремой 3 объем первой призмы равен произведению площади многоугольника 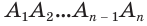 и высоты призмы, которая равна боковому ребру
и высоты призмы, которая равна боковому ребру 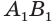 , а объем второй — произведению площади многоугольника
, а объем второй — произведению площади многоугольника 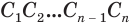 и той же высоты. Объем самого цилиндра заключен между этими объемами.
и той же высоты. Объем самого цилиндра заключен между этими объемами.
Будем количество 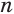 сторон оснований призмы делать все большим и большим. Тогда объем первой призмы увеличивается, объем второй — уменьшается, а разность между ними стремится к нулю, если количество сторон
сторон оснований призмы делать все большим и большим. Тогда объем первой призмы увеличивается, объем второй — уменьшается, а разность между ними стремится к нулю, если количество сторон 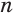 становится неограниченно большим. То число, к которому приближаются объемы обеих призм, принимается за объем цилиндра.
становится неограниченно большим. То число, к которому приближаются объемы обеих призм, принимается за объем цилиндра.
В описанном процессе высота 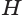 призмы остается равной боковому ребру, которое равно образующей
призмы остается равной боковому ребру, которое равно образующей 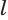 цилиндра, а площади многоугольников
цилиндра, а площади многоугольников 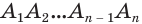 и
и 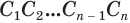 стремятся к площади
стремятся к площади 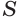 круга, лежащего в основании цилиндра. Значит, объем
круга, лежащего в основании цилиндра. Значит, объем 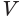 цилиндра равен произведению площади
цилиндра равен произведению площади 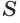 основания и образующей
основания и образующей 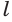 цилиндра:
цилиндра:
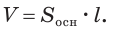
Поверхность цилиндра
Ещё один важный класс пространственных фигур – тела вращения. Цилиндр является одним из них, мы познакомимся с ним глубже. Свойства цилиндра похожи на свойства призм, мы последовательно изучим их.
Тело, полученное вращением прямоугольника вокруг одной из его сторон называют цилиндром (точнее, прямой круговой цилиндр) (рис. 75). При вращении прямоугольника одна его сторона остаётся неподвижной. Её называют осью цилиндра. Поверхность, образованную при вращении противоположной стороны прямоугольника называют цилиндрической поверхностью, а саму сторону образующей цилиндра. Две другие стороны прямоугольника при этом вращении образуют два равных круга, которые называют основаниями цилиндра (рис. 76). 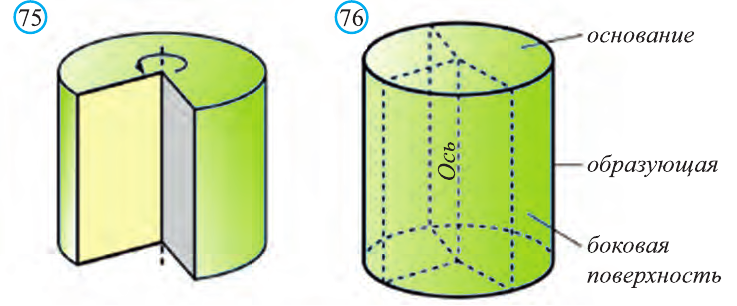
Замечание. Тело, полученное вращением прямоугольника вокруг одной из его сторон называют прямым круговым цилиндром. Более широкое понятие цилиндра вводят следующим образом.
Пусть в пространстве параллельный перенос переводит плоскую фигуру F1, в фигуру F2. Тело, состоящее из этих фигур и отрезков, соединяющих их соответствующие точки, называют цилиндром (рис. 77).
Если при параллельном переносе образующая перпендикулярна плоскости фигуры F1 , цилиндр называют прямым (рис. 78.а), в противном случае наклонным цилиндром (рис. 78.b). На рисунке 78.с изображена Пизанская башня, имеющая вид наклонного цилиндра. 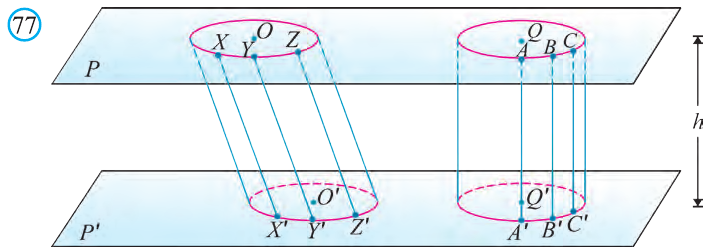
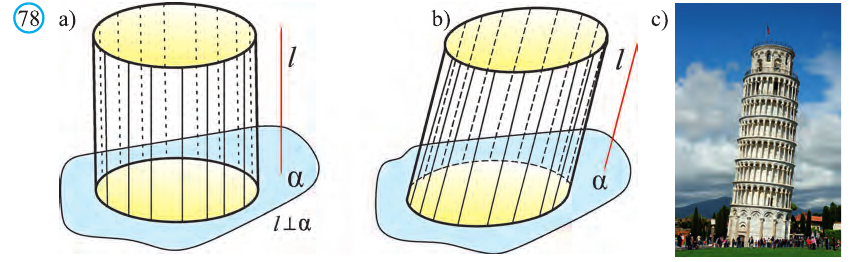
Если фигура F1 является кругом, то цилиндр называют круговым цилиндром.
Только прямой круговой цилиндр является телом вращения. В дальнейшем мы будем рассматривать прямые круговые цилиндры, которые для краткости будем называть цилиндрами.
Основания цилиндра являясь равными кругами, лежат на параллельных плоскостях. Перпендикуляр, опущенный из некоторой точки одного основания на другое, называют его высотой.
Расстояние между параллельными плоскостями равно высоте цилиндра. Ось цилиндра также является его высотой.
Образующие цилиндра параллельны и равны. Точно также, длины высоты, оси и образующих цилиндра будут равны между собой.
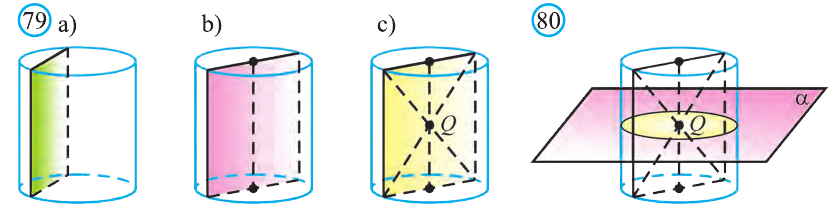
Сечением цилиндра плоскостью параллельной его оси является прямоугольник (рис.79.а). Две противоположные его стороны – это образующие цилиндра, а две другие стороны – соответствующие параллельные хорды оснований цилиндра.
В частности, осевое сечение также прямоугольник, образованный сечением цилиндра плоскостью, проходящей через его ось (рис. 79.b).
Диагонали осевого сечения цилиндра проходят через точку являющуюся серединой отрезка, соединяющего центры оснований цилиндра. Следовательно, эта точка Q есть центр симметрии цилиндра (рис. 79.с).
Плоскость, проходящая через точку Q перпендикулярно оси цилиндра является его плоскостью симметрии (рис. 80). Любая плоскость, проходящая через ось цилиндра также будет ось симметрии цилиндра (рис. 81).
Пример:
Осевое сечение цилиндра – квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Решение:
Сторона квадрата равна 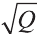 . Она равна диаметру
. Она равна диаметру
основания. Поэтому его площадь равна 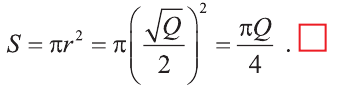
Докажите самостоятельно эту теорему пользуясь рисунком 82. 
Следствие. Полная поверхность цилиндра равна сумме его боковой поверхности и площадей двух его оснований:
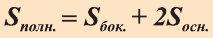 или
или 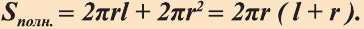
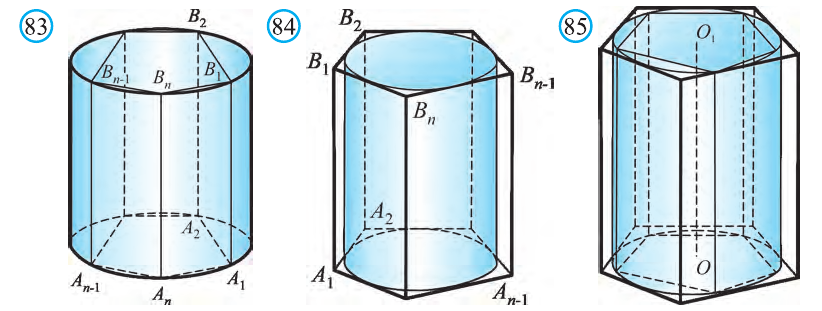
Пусть дан произвольный цилиндр. Впишем в одно из его оснований многоугольник 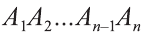 (рис. 83). Через вершины многогранника
(рис. 83). Через вершины многогранника 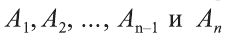 проведём образующие цилиндра
проведём образующие цилиндра 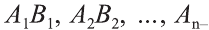
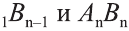 , другие концы которых
, другие концы которых 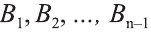 и
и 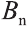 последовательно соединим отрезками. В результате получим призму
последовательно соединим отрезками. В результате получим призму 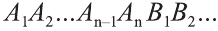
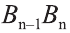 . Эту призму называют призмой, вписанной в цилиндр. А цилиндр называют цилиндром, вписанным в призму. Если призма вписана в цилиндр, то основание призмы будет вписано в основание цилиндра и боковые рёбра призмы будут лежать на боковой поверхности цилиндра.
. Эту призму называют призмой, вписанной в цилиндр. А цилиндр называют цилиндром, вписанным в призму. Если призма вписана в цилиндр, то основание призмы будет вписано в основание цилиндра и боковые рёбра призмы будут лежать на боковой поверхности цилиндра.
Ясно, что если вокруг основания призмы можно описать окружность, то вокруг призмы можно описать цилиндр.
Аналогично вводятся понятия призмы, описанной вокруг цилиндра и цилиндра, вписанного в призму (рис. 84). Если призма описана вокруг цилиндра, то основание призмы будет описано вокруг основания цилиндра и боковые грани призмы будут касаться боковой поверхности цилиндра.
Ясно, что если в основание призмы можно вписать окружность, то вокруг цилиндра можно описать призму.
Объём цилиндра
Теорема. Объём цилиндра равен произведению площади его основания и образующей цилиндра: 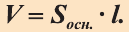
Доказательство. Пусть дан цилиндр с осью ОО1 (рис. 85). Впишем в него призму 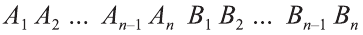 и опишем вокруг него призму
и опишем вокруг него призму 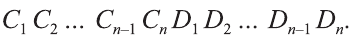 . Обозначим объём цилиндра V, а объёмы вписанной и описанной призм V1 и V2 , тогда имеет место двойное неравенство
. Обозначим объём цилиндра V, а объёмы вписанной и описанной призм V1 и V2 , тогда имеет место двойное неравенство 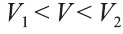 . Объёмы призм находят по следующим формулам:
. Объёмы призм находят по следующим формулам: 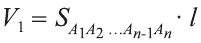 и
и
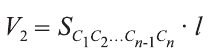
Будем всё больше и больше увеличивать число n сторон оснований призм. Тогда объём вписанной призмы будет увеличиваться, а объём описанной призмы уменьшаться. Если число n сторон увеличивать неограниченно, то разность между объёмами будет стремится к нулю. Число, к которому приближаются объёмы вписанной и описанной призм, принимают за объём данной призмы. При этом площади многогранников 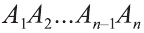 и
и 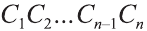 будут стремиться к площади S круга, лежащего в основании цилиндра. Следовательно,
будут стремиться к площади S круга, лежащего в основании цилиндра. Следовательно, 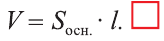
Исторические сведения:
В произведении Абу Райхна Беруни «Книга о началах искусства астрономии» («Астрономия») как введение в стереометрию в разделе о геометрии приводятся следующие определения фигур:
Куб – физическая фигура, похожая на кубик для игры в нарды, ограниченная с шести сторон квадратами.
Призма – представляет собой фигуру, ограниченную по бокам плоскостями в форме квадрата или прямоугольника, а сверху и снизу -двумя треугольниками. В этом определении Беруни приведено описание частного вида призмы, а именно треугольной призмы.
Книга Беруни «Канон Масьуда» написана в 1037 году. В ней приведены правила нахождения объёмов параллелепипеда и призмы: «Если тело не четырёхугольное или другого вида, то его расчёт таков: найди площадь, умножь его на глубину, в итоге получишь объём». В произведении Абу Али ибн Сино «Книга знания» в разделе «Основы изучения геометрических тел» дано описание тела и треугольной призмы. А также описаны условия взаимного равенства двух призм. Ибн Сино даёт следующее определение призмы: «Призма – тело, ограниченное двумя плоскими треугольными сторонами.»
В произведении Аль Каши «Книга счёта» приведёт много примеров расчета площадей поверхностей и объёмов тел. Благодаря своим глубоким знаниям в математике, геометрии, тригонометрии, механике и астрономии он пользовался вниманием и уважением Улугбека. Аль Каши наряду с многоугольниками изучачл призмы, пирамиды, цилиндры, конусы, усечённые конусы.

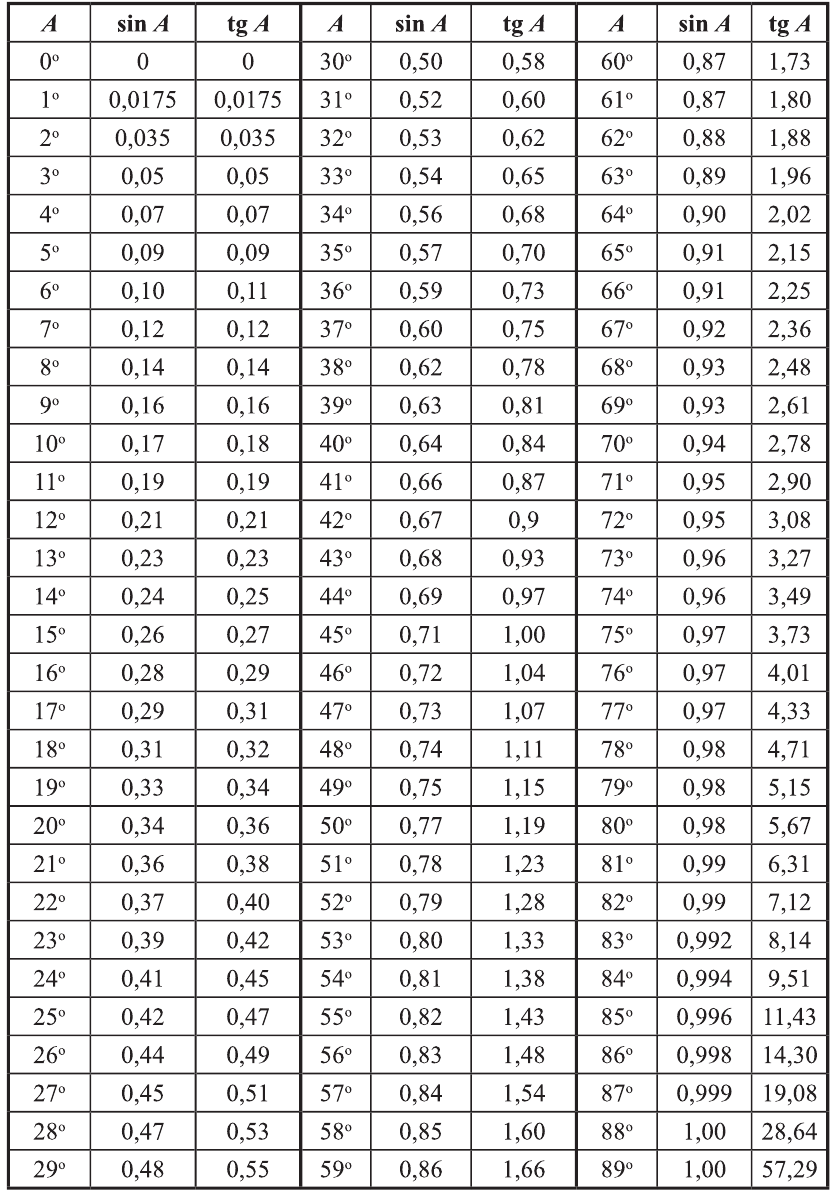
Таблица приближенных значений тригонометрических функций:
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Возникновение геометрии
- Призма в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
Вопрос, как найти объем цилиндра, может возникнуть не только у школьника. Ведь такую форму имеет, к примеру, кастрюля, емкость которой иногда срочно нужно узнать. Вот тогда потребуется знание специальной формулы.
Что нужно знать о цилиндре?
Геометрическое тело, о котором мы говорим, образуется в результате вращения прямоугольника вокруг одной из его сторон, и всегда будет прямым. То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.
Каким бы ни был вид тела, все равно нужно знать о том, как найти объем цилиндра. Но сначала нужно определиться с некоторыми теоретическими данными.
Как называются отдельные элементы цилиндра и что о них известно?
Отрезки, которые соединяют попарно соответствующие точки на двух основаниях, называются образующими. У любого цилиндра они равны и параллельны друг другу. Если он прямой, то длина образующей совпадает с высотой тела.
В основании может лежать окружность или эллипс, тогда цилиндр будет круговым или эллиптическим соответственно. В формулах этот факт потребуется учесть. Потому что чаще всего они даются для кругового цилиндра. В эллиптическом, до того как вычислить объем цилиндра, нужно будет узнать, по какой формуле определить площадь овала.
Формулы объема для прямого и наклонного цилиндров
Здесь и далее приняты такие обозначения.
| Буква-обозначение | математическая величина |
| V | объем |
| S | площадь основания |
| h | высота |
| r | радиус окружности |
| l | длина образующей |
| α | угол между образующей и основанием |
В любом случае потребуется формула, в которой высота тела, умножается на площадь основания. Она выглядит так:
V = Sh
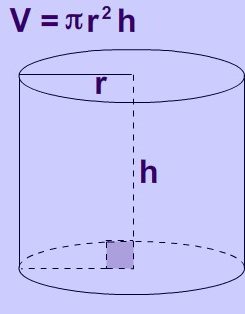
Если требуется узнать, как найти объем цилиндра прямого, то здесь высота по длине полностью совпадает с образующей. Основанием чаще всего является круг, тогда его площадь будет сосчитана по формуле:
S = πr2.
Когда в задаче идет речь об эллиптическом цилиндре, то потребуется такая формула площади основания:
S = π ab, здесь буквами a и b обозначены малая и большая полуоси овала.
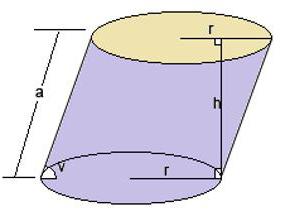
При решении задач о наклонном цилиндре потребуется ввести некоторые дополнения в формулу. Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением:
h = l * sin α.
Как быть, если нужно определить объем на практике?
В задачах обычно уже известны значения угла или высоты с образующей. А возможно, какие-то другие элементы, через которые их можно найти. В жизни приходится делать измерения самостоятельно.
Тогда вопрос о том, как определить объем цилиндра, сводится к тому, чтобы правильно сделать измерения его высоты и радиуса. Для этого потребуются: линейка, карандаш и прямоугольный лист бумаги.
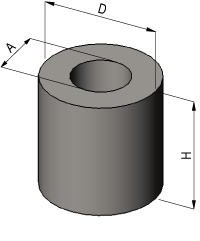
Чаще всего в быту нас окружают прямые круговые цилиндры. Измерить их высоту обычно не составляет труда. Нужно просто приложить линейку сбоку и измерить расстояние от низа до верха тела. Это будет высота — h.
С радиусом окружности все не так легко. Нужно немного вспомнить геометрию. Здесь потребуется лист бумаги с прямым углом и карандаш.
Что дает теория по геометрии? Вокруг прямоугольного треугольника можно описать окружность. Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.
Нужно взять лист бумаги и положить его так, чтобы прямой угол касался края основания. Тогда две его стороны, которые образуют этот угол, в некоторых точках пересекутся с окружностью. В этих местах потребуется сделать метки. По ним провести отрезок. Он окажется гипотенузой и искомым диаметром основания цилиндра.
Как найти объем цилиндра, в нашем случае? В формуле фигурирует радиус. Он равен половине диаметра. То есть длину получившегося отрезка нужно разделить на два.
Осталось только подставить результаты измерений в формулу объема и сосчитать. Причем учесть, что ответ получится в см3. Если объем нужно узнать в кубических метрах, то число нужно будет разделить на миллион. Чтобы получить объем в литрах, делителем окажется тысяча.
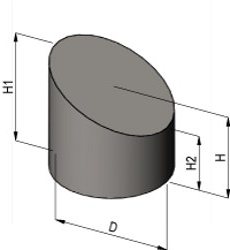
Задача
Условие. Даны два цилиндра. Высота первого в два раза больше второго. Радиус второго вдвое больше, чем у первого. Необходимо узнать, во сколько раз объем первого цилиндра больше или мегьше объема второго.
Решение. Сначала потребуется ввести обозначения. Пусть высота и радиус первого тела будут иметь индекс 1, а второго — 2.
Теперь можно записать данные в условии значения в виде выражений:
h1 = 2h2 и r2 = 2r1.
Формулы объемов обоих цилиндров примут такой вид:
v1 = π r12 h1 и v2 = π r22 h2.
В задаче требуется найти:
v1 : v2 = (π r12 h1) : (π r22 h2).
После сокращения πи замены h1 и r2введенными выражениями, получается:
v1 : v2 = (r12 2h2) : (4r12 h2).
То есть v1 : v2 = 1 : 2. Это означает, что объем первого цилиндра в два раза меньше.
Ответ. v1 = v2 : 2.
Объём прямого цилиндра онлайн
Значащих цифр:
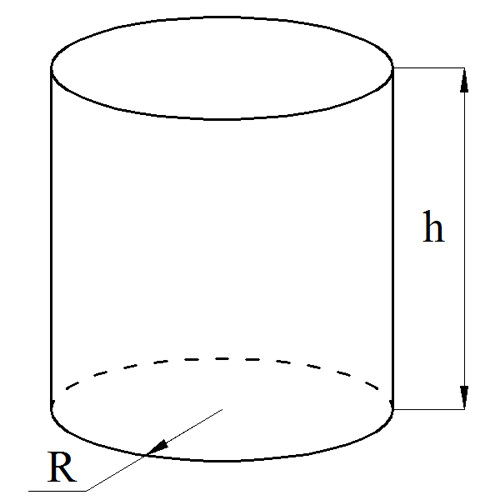
Формула объёма прямого цилиндра
Формула объёма прямого цилиндра через радиус
V=πR2h
Формула объёма прямого цилиндра через диаметр
V=πD2h/4
Формула объёма прямого цилиндра через площадь основания
V = Sh
где S это площадь основания прямого цилиндра
Определение цилиндра
Цилиндр(круговой цилиндр) – это тело, которое описывает плоский прямоугольник при вращении около оси, содержащей его сторону.
Цилиндр называется прямым если его образующие перпендикулярны плоскостям основания.
Высота цилиндра это перпендикуляр между основаниями цилиндра.
Образующая цилиндра это отрезок параллельный оси цилиндра, концы которого лежат на окружностях основания.
Образующая цилиндра это отрезок параллельный оси цилиндра, концы которого лежат на окружностях основания.
Радиус цилиндра это радиус основания.
Основания цилиндра это равные круги расположенные в параллельных плоскостях.
В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.
-
Формула вычисления объема цилиндра
- Через площадь основания и высоту
- Через радиус основания и высоту
- Через диаметр основания и высоту
- Примеры задач
Формула вычисления объема цилиндра
Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H

Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2)2 ⋅ H
Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см2, а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см2 ⋅ 10 см = 785 см3.
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)2 ⋅ 6 см = 301,44 см3.
Как узнать объем цилиндра
При решении математических и технических задач иногда требуется узнать объем цилиндра. Аналогичная задача часто возникает и в быту, так как многие емкости (бочки, ведра, банки и т.п.) имеют цилиндрическую форму. Конечно, если известны радиус и высота (длина) цилиндра, его объем очень легко вычислить. Однако на практике эти параметры не всегда заданы, да и цилиндры бывают не только прямые круговые.

Вам понадобится
- калькулятор
Инструкция
Чтобы узнать объем цилиндра, умножьте его высоту на число «пи» и на квадрат радиуса. В виде формулы это правило выглядит следующим образом:Об = В * π * Р², где Об – объем цилиндра, В – высота цилиндра, Р – радиус основания цилиндра, π – число «пи», примерно равное 3,14.Объем цилиндра будет измеряться в соответствующих радиусу и высоте кубических единицах измерения. Т.е. если, например, радиус и высота цилиндра будут заданы в метрах, его объем получится в кубометрах (м³).Вышеприведенное правило справедливо лишь для «обычного», т.е. прямого кругового цилиндра (цилиндра, основание которого представляет круг, а направляющая перпендикулярна ему).
Пример: высота цилиндра составляет 5 см, а радиус основания – 2 см. В этом случае его объем будет равен: 5 * π * 2² ≈ 62,831 см³.Число π имеется на многих калькуляторах и обозначается, как правило, греческой буквой «пи» (π). На виртуальной клавиатуре стандартного калькулятора Windows (в инженерном виде) число обозначено как pi.
Если вместо радиуса цилиндра задан его диаметр, воспользуйтесь следующей формулой:Об = В * π * (Д/2)² или Об = ¼ * В * π * Д², где Д – диаметр основания цилиндра.
Пример: высота и диаметр основания цилиндра равны 10 см. В этом случае, чтобы узнать объем, посчитайте значение следующего выражения: 10 * π * (10/2)² ≈ 785,398 см³.
На практике, обычно гораздо проще измерить периметр (длину окружности) основания цилиндра, чем его диаметр или радиус. Чтобы посчитать объем цилиндра, если известен периметр его основания, воспользуйтесь следующей формулой:Об = ¼ * В * П² / π, где П – периметр основания.При использовании этой формулы для расчета емкости тары (посуды) учтите, что реальная вместимость окажется немного меньше расчетной (на величину объема стенок сосуда).
Согласно определению, основанием цилиндра может быть произвольная линия на плоскости, а его образующая необязательно перпендикулярна основанию. В общем случае узнать объем цилиндра можно по следующим правилам:- объем цилиндра равен произведению длины образующей на площадь сечения цилиндра плоскостью, которая перпендикулярна образующей;
– объем цилиндра равен произведению площади основания на высоту (расстояние между основаниями).
Видео по теме
Обратите внимание
Высота цилиндра – понятие чисто геометрическое. Она означает лишь расстояние между его основаниями и не зависит от расположения цилиндра в пространстве.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
