Масса полой детали
Никогда не устану повторять, что масса тела — это его объем  , умноженный на плотность его материала
, умноженный на плотность его материала  (см. таблицы плотностей):
(см. таблицы плотностей):

Однако, в случае полой или пустотелой детали мы будем иметь дело не с объемом ее тела, а с объемом ее стенок. Объем стенок полой детали проще всего представить как разность объемов двух сплошных тел: с внешними размерами и с внутренними (из полного объема тела вычитается объем внутренней пустоты).
Формулы для объема сплошных тел можно найти в статье «Масса сплошной детали».
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой  обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
1. Масса трубки (полого цилиндра)
 Объем стенок трубки:
Объем стенок трубки:  , где
, где  — внешний диаметр трубки,
— внешний диаметр трубки,  — длина трубки,
— длина трубки,  — толщина стенки.
— толщина стенки.
После упрощения получаем формулу для объема: 
Тогда масса трубки:

2. Масса полого (пустотелого) шара
 Объем стенок шара:
Объем стенок шара:  , где
, где  — внешний диаметр шара,
— внешний диаметр шара,  — толщина стенки.
— толщина стенки.
Тогда масса:

3. Масса полого сегмента шара
 Объем стенок сегмента шара:
Объем стенок сегмента шара:  , где
, где  — внешний диаметр основания сегмента,
— внешний диаметр основания сегмента,  — высота сегмента,
— высота сегмента,  — толщина стенки*.
— толщина стенки*.
После упрощения получаем формулу для объема: 
Тогда масса:

4. Масса полого усеченного конуса
 Объем стенок круглого усеченного конуса:
Объем стенок круглого усеченного конуса:  , где
, где  — внешний диаметр большего основания,
— внешний диаметр большего основания,  — внешний диаметр меньшего основания,
— внешний диаметр меньшего основания,  — высота конуса,
— высота конуса,  — толщина стенки*.
— толщина стенки*.
После упрощения получаем формулу для объема: 
Тогда масса:

5. Масса полой усеченной пирамиды
 Для простоты рассмотрим усеченную пирамиду с квадратным основанием. Объем ее стенок:
Для простоты рассмотрим усеченную пирамиду с квадратным основанием. Объем ее стенок:  , где
, где  — внешний размер большего основания,
— внешний размер большего основания,  — внешний размер меньшего основания,
— внешний размер меньшего основания,  — высота пирамиды,
— высота пирамиды,  — толщина стенки*.
— толщина стенки*.
После упрощения получаем формулу для объема: 
Тогда масса:

* в данном случае  — это не вполне толщина стенки. Строго говоря, мы имеем тут дело с двумя величинами: та
— это не вполне толщина стенки. Строго говоря, мы имеем тут дело с двумя величинами: та  , что стоит в формулах за скобкой, это точно толщина стенки, а та
, что стоит в формулах за скобкой, это точно толщина стенки, а та  , которую мы отнимаем от внешнего размера тела, чтобы получить его внутренний размер, — это толщина стенки, деленная на косинус угла наклона образующей. Но в большинстве случаев толщина стенки не превышает нескольких процентов от размеров тела, и ошибкой можно пренебречь. Однако, для толстостенных деталей это обстоятельство нужно учитывать.
, которую мы отнимаем от внешнего размера тела, чтобы получить его внутренний размер, — это толщина стенки, деленная на косинус угла наклона образующей. Но в большинстве случаев толщина стенки не превышает нескольких процентов от размеров тела, и ошибкой можно пренебречь. Однако, для толстостенных деталей это обстоятельство нужно учитывать.
Объем через массу и плотность, формула
Объем тела выражается через массу и плотность следующей формулой:
Объем тела — есть отношение массы тела к плотности вещества из которого состоит тело.
[ V = frac{m}{ρ} ]
Здесь:
V — объем тела (м³),
m — масса тела, (килограмм),
ρ — плотность вещества, (кг/м³).
Вычислить, найти объем твердых тел или жидкостей через массу и плотность по формуле (1)
Выберите вещество ▼
| m (масса, килограмм) |
| ρ (плотность вещества, x103 кг/м³) |
Вычислить
нажмите кнопку для расчета
Вычислить, найти объем газа через массу и плотность по формуле (1)
Выберите вещество ▼
| m (масса газа, килограмм) |
| ρ (плотность газа, кг/м³) |
Вычислить
нажмите кнопку для расчета
Объем через массу и плотность |
стр. 444 |
|---|
Найти массу, плотность или объем онлайн
На данной странице калькулятор поможет найти плотность, массу или объем вещества онлайн. Для расчета введите значения в калькулятор.
Объем, масса и плотность
Найти
Масса:
Объем:
Плотность:
Ответы:
Формула для нахождения массы тела через плотность и объем:
m – масса; V – объем; p – плотность.
Формула для нахождения объема тела через плотность и массу:
m – масса; V – объем; p – плотность.
Формула для нахождения плотности тела через объем и массу:
m – масса; V – объем; p – плотность.
Калькулятор
 Главная
Главная  Учёба
Учёба  Объем цилиндра
Объем цилиндра  Объём полого цилиндра
Объём полого цилиндра
Объём полого цилиндра
Формула вычисления объема полого цилиндра часто применяются при расчете массы полой круглой трубы.
Эти онлайн калькуляторы производят расчёты по следующим формулам.
Другая Формула
Объём полого цилиндра через внутренний и наружный радиусы
Формула расчёта: V = pi*(r1[в квадрате]-r2[в квадрате])*h
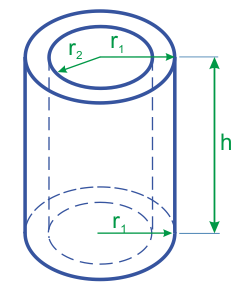
| Радиус наружный (r1) | ||
| Радиус внутренний (r2) | ||
| Высота (h) |
Объём полого цилиндра по толщине стенки и наружному диаметру
Формула расчёта: 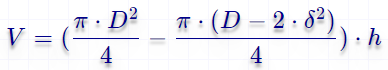
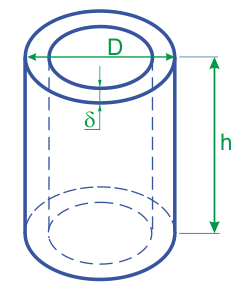
| Внешний диаметр (D) | ||
| Толщина стенки (δ) | ||
| Высота (h) |
Объём полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки
Формула расчёта: V = pi*(d*δ+δ2)*h
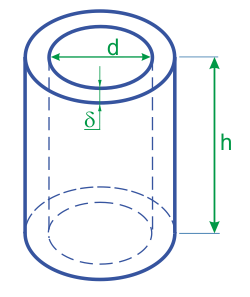
| Внутренний диаметр (d) | ||
| Толщина стенки (δ) | ||
| Высота (h) |
Площадь полого цилиндра
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |
Чтобы узнать объем грузов, перевозимых в рулонах (ткани, ковры, шторы, резиновые покрытия) необходимо воспользоваться формулой расчета объема цилиндра.
Чтобы определить объем цилиндра по радиусу, необходимо произвести расчет по формуле:
- V=π·r²·h
-

π — константа равная (3.14);
r — радиус основания;
h — высота цилиндра.
