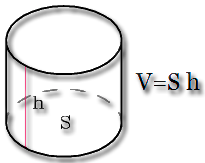
{V= pi R^2 h}
Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон.
Другое определение: цилиндр – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Рассчитать объем цилиндра можно по нескольким формулам. Для расчета необходимо знать высоту цилиндра и один из параметров – радиус основания, диаметр основания или площадь основания.
Содержание:
- калькулятор объема цилиндра
- формула объема цилиндра через высоту и радиус
- формула объема цилиндра через высоту и площадь основания
- формула объема цилиндра через высоту и диаметр
- примеры задач
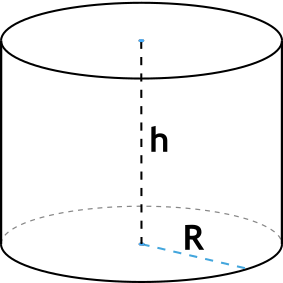
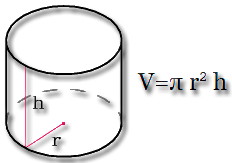
Формула объема цилиндра через высоту и радиус
{V= pi R^2 h}
R – радиус основания цилиндра
h – высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что {pi R^2} – это формула площади круга, а в нашем случае – площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
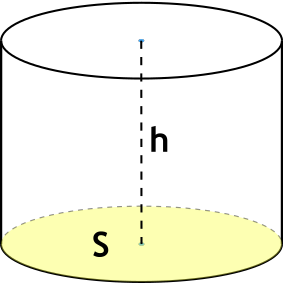
Формула объема цилиндра через высоту и площадь основания
{V= S h}
S – площадь основания цилиндра
h – высота цилиндра
Так как диаметр окружности равен двум радиусам, мы легко можем преобразовать формулу объема цилиндра через радиус и высоту в формулу через диаметр и высоту. Для этого выразим радиус через диаметр и получим необходимую формулу:
D = 2R to R = dfrac{D}{2}
V = pi R^2 h = pi {Big( dfrac{D}{2} Big) }^2 h = pi dfrac{D^2}{4} h
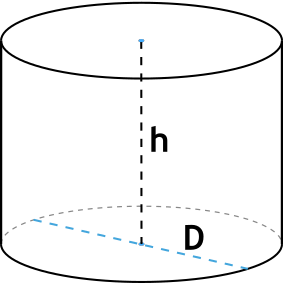
Формула объема цилиндра через высоту и диаметр
{V= pi {dfrac{D^2}{4}} h}
D – диаметр основания цилиндра
h – высота цилиндра
Примеры задач на нахождение объема цилиндра
Задача 1
Найти объём цилиндра с высотой 3см и диаметром основания 6см.
Решение
Так как в условии задачи нам дан диаметр основания цилиндра, мы будем использовать формулу объема через диаметр. Подставим в нее известные высоту и диаметр, чтобы получить объем цилиндра.
V = pi dfrac{D^2}{4} h = pi dfrac{6^2}{4} 3 = pi dfrac{36}{4} 3 = pi cdot 9 cdot 3 = 27 pi : см^3 approx 84.823 : см^3
Ответ: 27 pi : см^3 approx 84.823 : см^3
Ответ легко проверить с помощью калькулятора .
Задача 2
Найдите объем цилиндра с радиусом основания 5см и высотой 16см.
Решение
Для решения этой задачи воспользуемся формулой объема через радиус.
V = pi R^2 h = pi cdot 5^2 cdot 16 = pi cdot 25 cdot 16 = pi cdot 25 cdot 16 = 400 pi : см^3 approx 1 256.63706 : см^3
Ответ: 400 pi : см^3 approx 1 256.63706 : см^3
Проверить ответ поможет калькулятор .
Что бы узнать объем цилиндра вам нужно знать высоту, радиус или площадь, всего есть две основные формулы – площадь основания и высота и радиус и высота.
Самый простой способ это умножить площадь основания цилиндра на его высоту.
Калькуляторы объема цилиндра
- Выберете величины для вычисления – обязательно нужно знать высоту, площадь основания или диаметр цилиндра.
- Для результата введите известные значения величин.
- Выберете нужный показатель результата и вводные в куб. мм, куб. см, куб. м, куб. дюйм.
- Активируйте калькулятор и получите результат (значение не округляются).
Если после использования данного онлайн калькулятора
(Расчет объема цилиндра) у вас возникли какие-то вопросы по работе сервиса или вопросы
образовательного характера, то Вы всегда можете задать их на нашем
форуме.
Определение цилиндра
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра). Цилиндр – круговой если в основании его лежит круг.
Формулы для вычисления объема цилиндра
Формула объема цилиндра через площадь основания и высоту:
$ V = S h $ где:
S – площадь основания
h – высота цилиндра
Формула объема цилиндра через радиус и высоту:
$ V = pi r^2 h$ где:
π – число пи (3.1415);
h – высота цилиндра;
r – радиус основания.
Примеры решений:
Пример 1
Определить, чему равен объем цилиндра, если радиус его основания R равна $225 pi mathrm{cm}^{2}$ , высота равна h в 5 раз болше R.
Решение:
$S_{mathrm{ocH}}=225 pi$
$h=5 cdot R$
Вычисляем радиус основания:
$S_{mathrm{ocH}}=pi cdot R^{2}$
Выразим радиус R:
$R^{2}=frac{S_{mathrm{och}}}{pi}$
$R=sqrt{frac{S_{mathrm{ock}}}{pi}}$
$R=sqrt{frac{225 pi}{pi}}$
$R=sqrt{225}$
$R=15$
Вычисляем высоту:
$h=5 cdot R=5 cdot 15=75$
Вычисляем объем цилиндра по формуле:
$V=S_{mathrm{ocH}} cdot h=225 cdot pi cdot 75 approx 52950 mathrm{~cm}^{3}$
Результат:$approx 52950 mathrm{~cm}^{3}$
Пример 2
Найти чему равен объем цилиндра, если радиус основанияравен 17 см, а высота – 140 см
Решение:
R = 17
h = 140
Высчитываем по формуле:
$V=S_{mathrm{ocH}} cdot h=pi cdot R^{2} cdot h=pi cdot 17^{2} cdot 140 approx 127108 mathrm{~cm}^{3}$
Результат:$approx 127108 mathrm{~cm}^{3}$
Как рассчитать объем цилиндра
На данной странице калькулятор поможет рассчитать объем цилиндра онлайн. Для расчета задайте высоту, радиус или площадь основания. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
По высоте и радиусу
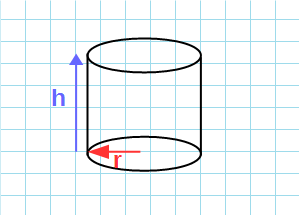
Формула объема цилиндра через высоту и радиус:
V=π·r²·h
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Через площадь основания и высоту
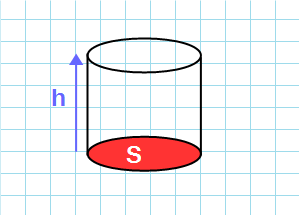
Формула объема цилиндра через высоту и площадь основания:
V=S·h
S – площадь основания цилиндра; h – высота цилиндра.
Как посчитать объем цилиндра
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать объем цилиндра
Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра если его радиус
r = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
V = π⋅r2⋅h
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3
Зная диаметр d и высоту h
Чему равен объем цилиндра если его диаметр
d = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
V = π⋅(d/2)2⋅h
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
Зная площадь основания So и высоту h
Чему равен объем цилиндра если площадь его основания
So = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
V = So⋅h
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см2, то:
V = 10 ⋅ 5 = 50 см3
Зная площадь боковой поверхности Sb и высоту h
Чему равен объем цилиндра если площадь его боковой поверхности
Sb = ,
а высота
h = ?
Ответ: V =
0
Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
V = Sb2/4πh
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см2, то:
V = 302/ 4 ⋅ 3.14⋅ 5 = 900/62.8 = 14.33 см3
См. также
Калькулятор объема цилиндра, формула, расчет
Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Также определение можно перефразировать, и сказать, что цилиндр — это геометрическое тело, которое получается при вращении прямоугольника вокруг одной из его стороны.
Формула объема цилиндра: V = π×r²×h, где r — радиус оснований, h — высота цилиндра S – это площадь основания, h – это высота цилиндра, π = 3,14159. π×r² — это площадь основания цилиндра (S). Если площадь основания известна, то формулу объема цилиндра можно записать в следующем виде: V = S×h.
Объем цилиндра можно рассчитать самостоятельно по приведенным выше формулам. Также можно воспользоваться онлайн калькуляторами объема цилиндра.
Объем цилиндра через радиус и высоту — онлайн расчет
Для расчета объема цилиндра введите радиус, высоту и нажмите кнопку вычислить.
Объем цилиндра через площадь основания — калькулятор
Для расчета объема цилиндра введите площадь основания, высоту и нажмите кнопку вычислить.