Как определить объём цилиндра при его погружении в воду?
Анонимный вопрос
2 декабря 2018 · 12,0 K
Инженер по профессии, люблю спорт, музыку, кино. · 2 дек 2018
Согласно закону Архимеда, объем тела, погруженного в воду равен объему вытесненной им воды.
Чтобы определить таким образом объем цилиндра, нужно взять мерный стакан с водой со шкалой объема. Определить по шкале первоначальный объем воды – V1.
Затем погружаем цилиндр в воду и отмечаем объем воды после погружения – V2.
Тогда объем цилиндра бует равен разности конечного и начального объемов воды:
V = V2 – V1.
11,7 K
Комментировать ответ…Комментировать…
888
Знаток
(463),
на голосовании
13 лет назад
Голосование за лучший ответ
Захар Иванов
Мастер
(1525)
13 лет назад
Площадь основания умножить на высоту.
Иван Афанасьев
Ученик
(144)
13 лет назад
V=3.14*(r^2)*H, где r-радиус цилиндра, H-высота цилиндра
Влад Храмов
Ученик
(113)
7 лет назад
помогите срочно как решить эту задачу V=3.14(r во 2)H
V= 3.14*(0.25)*1
Похожие вопросы
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1. Определите цену деления мензурки.
2. Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3. Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201), и снова измерьте объём жидкости.
4. Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5. Результаты измерений запишите в таблицу 9.
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9.

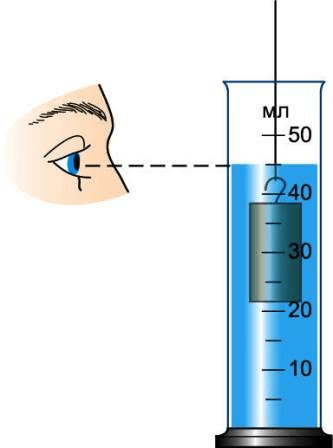
рис. 201
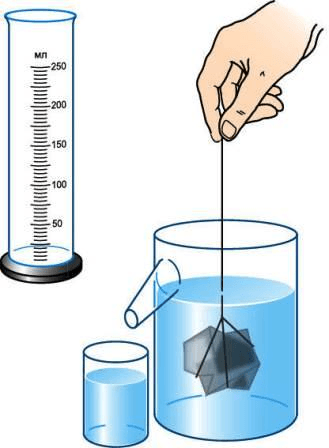
рис. 202

reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
V
=
V
2
−
V
1
, где
V
2
− объём воды и тела,
V
1
− начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30.
Таким образом, цена каждого деления будет равна
30
−
202
=
10
= 5 мл.
2 - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70
с
м
3
. - Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
V
б
р
=
95
−
70
=
25с
м
3
V
ц
=
85
−
65
=
20с
м
3
V
ш
=
75
−
60
=
15с
м
3
- Результаты измерений запишем в таблицу 9.
Таблица 9.
| № опыта | Название тела | Начальный объём воды в мензурке
V 1 , с м 3 |
Объём воды и тела
V 2 , с м 3 |
Объём тела V,
с м 3 V = V 2 − 1 |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Просмотров: 5 562
Задание 7 ОГЭ по физике, демоверсия 2018:
К динамометру прикрепили цилиндр, как показано на рисунке 1. Затем цилиндр полностью погрузили в воду (рисунок 2).

Определите объём цилиндра.
Ответ: ___________________________ см3.
Будем благодарны, если вы поделитесь данной записью со своими друзьями в социальных сетях, оставите отзыв и посмотрите другие материалы на нашем сайте.
Вконтакте
Одноклассники
Мой мир

{V= pi R^2 h}
Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон.
Другое определение: цилиндр – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Рассчитать объем цилиндра можно по нескольким формулам. Для расчета необходимо знать высоту цилиндра и один из параметров – радиус основания, диаметр основания или площадь основания.
Содержание:
- калькулятор объема цилиндра
- формула объема цилиндра через высоту и радиус
- формула объема цилиндра через высоту и площадь основания
- формула объема цилиндра через высоту и диаметр
- примеры задач
Формула объема цилиндра через высоту и радиус
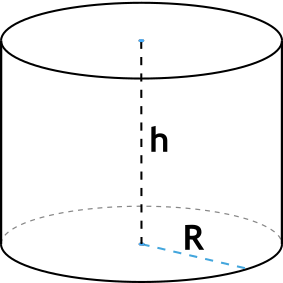
{V= pi R^2 h}
R – радиус основания цилиндра
h – высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что {pi R^2} – это формула площади круга, а в нашем случае – площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
Формула объема цилиндра через высоту и площадь основания
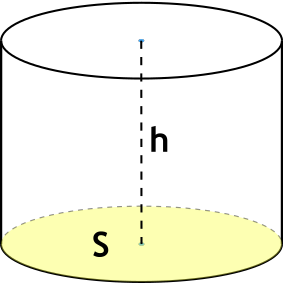
{V= S h}
S – площадь основания цилиндра
h – высота цилиндра
Так как диаметр окружности равен двум радиусам, мы легко можем преобразовать формулу объема цилиндра через радиус и высоту в формулу через диаметр и высоту. Для этого выразим радиус через диаметр и получим необходимую формулу:
D = 2R to R = dfrac{D}{2}
V = pi R^2 h = pi {Big( dfrac{D}{2} Big) }^2 h = pi dfrac{D^2}{4} h
Формула объема цилиндра через высоту и диаметр
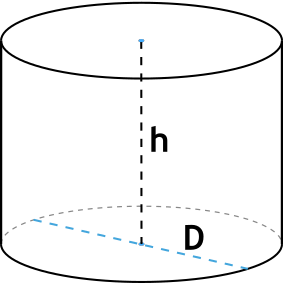
{V= pi {dfrac{D^2}{4}} h}
D – диаметр основания цилиндра
h – высота цилиндра
Примеры задач на нахождение объема цилиндра
Задача 1
Найти объём цилиндра с высотой 3см и диаметром основания 6см.
Решение
Так как в условии задачи нам дан диаметр основания цилиндра, мы будем использовать формулу объема через диаметр. Подставим в нее известные высоту и диаметр, чтобы получить объем цилиндра.
V = pi dfrac{D^2}{4} h = pi dfrac{6^2}{4} 3 = pi dfrac{36}{4} 3 = pi cdot 9 cdot 3 = 27 pi : см^3 approx 84.823 : см^3
Ответ: 27 pi : см^3 approx 84.823 : см^3
Ответ легко проверить с помощью калькулятора .
Задача 2
Найдите объем цилиндра с радиусом основания 5см и высотой 16см.
Решение
Для решения этой задачи воспользуемся формулой объема через радиус.
V = pi R^2 h = pi cdot 5^2 cdot 16 = pi cdot 25 cdot 16 = pi cdot 25 cdot 16 = 400 pi : см^3 approx 1 256.63706 : см^3
Ответ: 400 pi : см^3 approx 1 256.63706 : см^3
Проверить ответ поможет калькулятор .
