Задания
Версия для печати и копирования в MS Word
Тип 2 № 72283 
i
В основании прямой призмы лежит квадрат со стороной 6. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
Решение.
Это задание ещё не решено, приводим решение прототипа.
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
Диагональ квадрата, лежащего в основании призмы, является диаметром описанного вокруг призмы цилиндра. Тогда объем цилиндра:
Ответ: 4.
Аналоги к заданию № 27050: 72303 4973 4975 … Все
Классификатор стереометрии: Объём цилиндра, конуса, шара
Прототип задания
·
Видеокурс
Решение.
Найдем диагональ основания призмы, исходя из информации о размере ребер ее основания.
По теореме Пифагора, найдем квадрат гипотенузы треугольника, лежащего в основании.
7^2 + 8^2 = 113
Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
Таким образом, цилиндр, описанный около заданной призмы, будет иметь диаметр, равный гипотенузе прямоугольного треугольника, лежащего в основании призмы и высоту, равную высоте призмы. Таким образом, объем цилиндра составит:
V= пr2h, где
п – число пи
r – радиус основания цилиндра
h – высота цилиндра
Поскольку гипотенуза прямоугольного треугольника, лежащего в основании призмы одновременно является диаметром цилиндра, описанного вокруг призмы, то радиус цилиндра будет равен половине гипотенузы, то есть квадратный корень из 113 деленный пополам, а квадрат радиуса, соответственно равен r2=113/4.
По условию задачи высота ребра призмы равна 8/п .
Таким образом:
V=п*113/4*8/п
V=226
Ответ: 226
Задача 1. Объем прямоугольного параллелепипеда, описанного около сферы, равен Найдите радиус сферы.
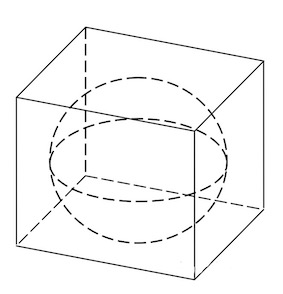
Решение: + показать
Задача 2. В куб вписан шар радиуса Найдите объем куба.

Решение: + показать
Задача 3. Шар, объём которого равен вписан в куб. Найдите объём куба.

Решение: + показать
Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен Объем параллелепипеда равен
Найдите высоту цилиндра.
Решение: + показать
Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объем параллелепипеда.
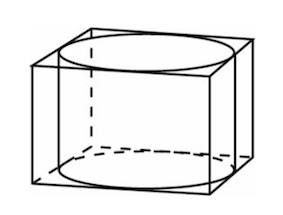 Решение: + показать
Решение: + показать
Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны Найдите площадь боковой поверхности призмы.
Решение: + показать
Задача 7. В основании прямой призмы лежит квадрат со стороной . Боковые ребра равны
Найдите объем цилиндра, описанного около этой призмы.
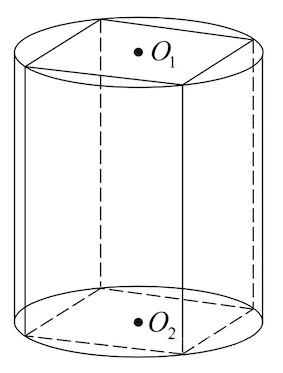
Решение: + показать
Задача 8. Около шара описан цилиндр, площадь поверхности которого равна Найдите площадь поверхности шара.
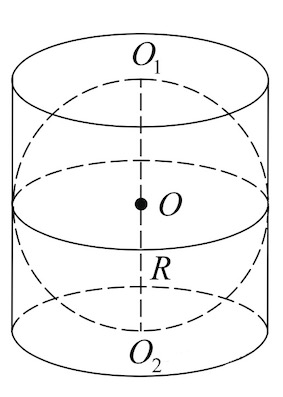
Решение: + показать
Задача 9. Цилиндр описан около шара. Объем цилиндра равен Найдите объем шара.

Решение: + показать
Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
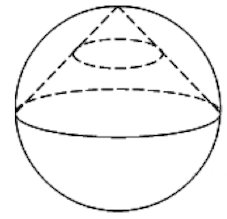
Решение: + показать
Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен Найдите объем шара.

Решение: + показать
Задача 12. Середина ребра куба со стороной является центром шара радиуса
Найдите площадь
части поверхности шара, лежащей внутри куба. В ответе запишите
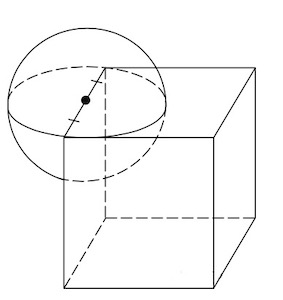
Решение: + показать
Задача 13. Вершина куба
со стороной
является центром сферы, проходящей через точку
. Найдите площадь
части сферы, содержащейся внутри куба. В ответе запишите величину
.
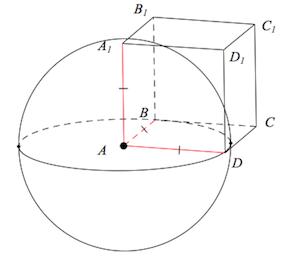
Решение: + показать
Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен
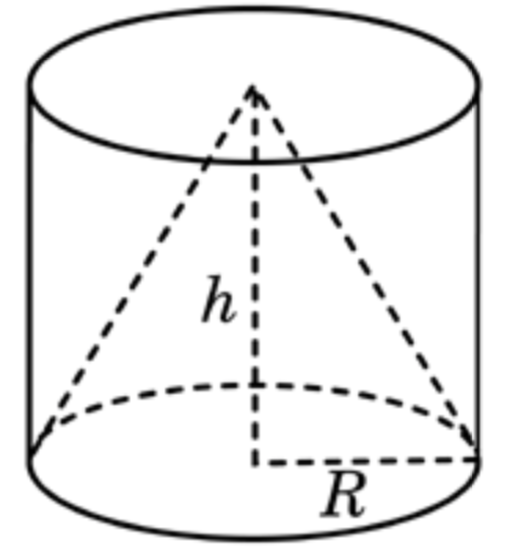
Решение: + показать
Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.

Решение: + показать
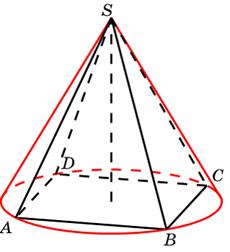
Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания и высотой
Найдите его объем, деленный на
.
Решение: + показать
Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
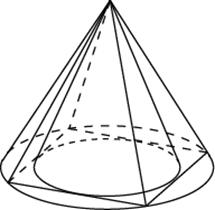
Решение: + показать
Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
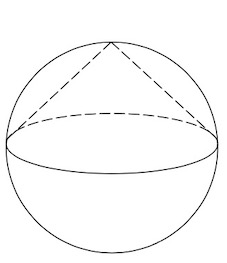
Решение: + показать
Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.

Решение: + показать
Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами и
Боковые ребра равны
. Найдите объем цилиндра, описанного около этой призмы.
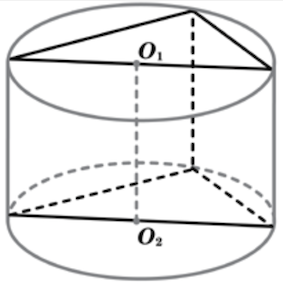
Решение: + показать
Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна
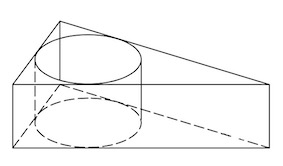
Решение: + показать
Задача 22. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен а высота равна
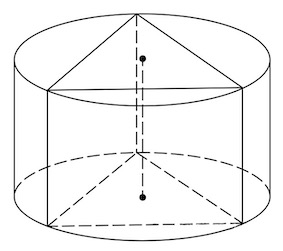
Решение: + показать
Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен

Решение: + показать
Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 26. Около куба с ребром описан шар. Найдите объем этого шара, деленный на
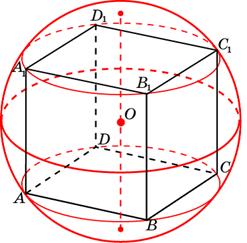
Решение: + показать
Задача 27. Куб вписан в шар радиуса Найдите объем куба.

Решение: + показать
 Вы можете пройти тест “Комбинация тел”
Вы можете пройти тест “Комбинация тел”
Перейти к контенту
Задание
В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
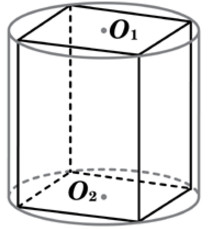
Решение
- Объем цилиндра равен произведению его высоты на площадь основания. А площадь основания равна площади круга: V=h*Socн=h*π*r2.
- Высота цилиндра известна, она равна боковому ребру призмы, то есть 2/π.
- Осталось найти площадь основания.
В основании лежит квадрат, причем по рисунку видим, что диагональ данного квадрата проходит через центр основания, тем самым являясь диаметром круга, лежащего в основании цилиндра.
Данная диагональ разбивает квадрат на два прямоугольных треугольника. Поэтому найдем диагональ (которая является диаметром) по теореме Пифагора:
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
D2 = 72+72 = 49+49 = 98
D = √98 — диаметр основания цилиндра.
- Найдем площадь основания:
S = π*(√98/2)2 = 24,5π
- Осталось найти объем цилиндра:
V = 2/π*24,5π = 49 – объем цилиндра.
Ответ: 49
Прямоугольный параллелепипед описан около
![]()
Дорогие друзья! В этой публикации мы рассмотрим ещё несколько заданий с комбинацией двух тел – призмы и цилиндра, одно из них вписано в другое. Ставится вопрос о вычислении объёма одного из указанных тел. Конечно же, необходимо знать соответствующие формулы, понимать, что высоты таких тел равны (они общие).
Кроме этого, в одном из типов представленных задач используется свойство прямоугольного треугольника вписанного в окружность, его мы подробно (с доказательством) рассмотрели здесь. Рассмотрим задачи:

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Радиус основания цилиндра равен 1. Это означает, что оба рёбра параллелепипеда в его основании равны 2. Высота общая. Таким образом, искомый объём:
![]()
Ответ: 4

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 8. Объем параллелепипеда равен 128. Найдите высоту цилиндра.

Так как высота цилиндра и параллелепипеда общая, то вычислив высоту параллелепипеда мы естественно найдём высоту цилиндра.
Основанием параллелепипеда является квадрат, сторона которого равна диаметру цилиндра, то есть двум его радиусам. Поэтому сторона основания будет равна 16.
Объём параллелепипеда равен произведению трёх его рёбер, третье ребро это высота:
![]()
Ответ: 0,5

В основании прямой призмы лежит прямоугольный треугольник с катетами 12 и 16. Боковые ребра равны 3/Пи. Найдите объем цилиндра, описанного около этой призмы.

Объём цилиндра равен:
![]()
Известно, что гипотенуза прямоугольного треугольника вписанного в окружность является диаметром этой окружности. По теореме Пифагора длина гипотенузы прямоугольного треугольника будет равна:
![]()
Значит радиус цилиндра будет равен 10, вычислим его объём:
![]()
Ответ: 300

В основании прямой призмы лежит квадрат со стороной 6. Боковые ребра равны 4/Пи. Найдите объем цилиндра, описанного около этой призмы.

Для нахождения объёма цилиндра необходимо найти площадь его основания (или радиус основания):
![]()
Основание цилиндра это круг, диаметр которого совпадает с диагональю квадрата. Диагональ квадрата в основании призмы можем найти по теореме Пифагора:
![]()
Получили, что радиус круга (цилиндра) равен 6√2.
Таким образом, вычислим искомый объем:

Ответ: 288
![]()
27042. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Посмотреть решение
27049.В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны 5/Пи. Найдите объем цилиндра, описанного около этой призмы.

Посмотреть решение
27050. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/Пи. Найдите объем цилиндра, описанного около этой призмы.

Посмотреть решение
Нf этом всё. Успеха Вам!
C уважением, Александр.
*Делитесь информацией в социальных сетях.
Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2Объём
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
