Ученик
(161),
закрыт
9 лет назад
Оракул
Оракул
(52849)
9 лет назад
диагональ осевого сечения – есть гипотенуза прямоугольного треугольника
диаметр – нижний катет
находите второй катет – он есть высота цилиндра
h = /18^2 – 4^2 = /308
Объем V = h * S
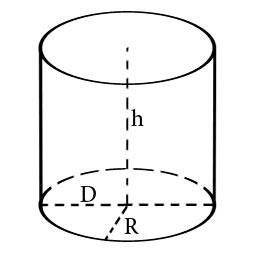
S = pi r^2 = 4pi – площадь основания
V = 4 pi /308
Вопрос о том, как найти объем цилиндра, может возникнуть не только у школьника, который занимается изучением стереометрии. На сегодняшний день очень популярны обтекаемые и плавные формы в архитектуре и дизайне интерьера. К ним относится и цилиндр. Сам по себе он является телом вращения – прямоугольником, который прокрутили на 360 градусов вокруг одной из сторон. Такую форму имеют колонны, поршни, кастрюли, чашки, стаканы, вазы и т. д. Конечно, в быту редко может пригодиться информация о нахождении объема цилиндра, но в школе этой теме уделяют достаточно много времени, так что игнорировать ее не стоит.
Стандартный способ определения объема цилиндра
Для того чтобы понять особенности объема цилиндра, нужно вернуться к теме параллелепипеда. Это тело имеет основу в виде прямоугольника или квадрата. Для расчета объема такой геометрической фигуры нужно умножить площадь основы (S = a × b) на высоту. С цилиндром все по аналогии. Основой выступает круг, формула площади которого S = πR2. Высота – это любая вертикальная линия, чаще всего выбирают ту, которая соединяет центры основ.
Как найти объем цилиндра по диагонали сечения?
Иногда может случиться такое, что в условиях не будет нужных величин, тогда необходимо будет находить их по рисунку, используя свойства цилиндра. Самым частым примером такого случая являются задачи, в которых известна диагональ сечения и одна из составляющих формулы объема – радиус или высота. Задание с подобным условием можно считать типичным для этой темы. Для решения нужно помнить только одну вещь: высота цилиндра – это любая вертикальная линия, которая соединяет основы и создает с ними угол в 90 градусов. Пользуясь этой особенностью, можно с легкостью определить, что диагональ сечения (которым является куб или прямоугольник), радиус и высота создают вместе треугольник. Его стороны можно найти по теореме Пифагора.
Зная диаметр цилиндра, можно вычислить радиус цилиндра и периметр окружности цилиндра, которая представляет собой его основание. Радиус будет равен одной второй диаметра, а периметр окружности – произведению диаметра на число π.
r=D/2
P=πD
Первое, что можно вычислить через диаметр и диагональ цилиндра – это его высота. Так как высота непосредственно связана со всеми остальными параметрами цилиндра, такими как площадь, объем и прочие, то она является необходимым звеном для геометрического калькулятора цилиндра. (рис.25.1)
h=√(d^2-D^2 )
Площадь боковой поверхности цилиндра равна произведению высоты на длину окружности в основании цилиндра, таким образом, раскрывая эту формулу, получаем, что площадь боковой поверхности равна произведению числа π и диаметра на квадратный корень из разности квадратов диагонали и диаметра.
S_(б.п.)=hP=πD√(d^2-D^2 )
Площадь полной поверхности цилиндра представлена площадью боковой поверхности в сумме с площадью двух оснований в виде окружностей.
S_(п.п.)=S_(б.п.)+2S_(осн.)=πD(√(d^2-D^2 )+D)
Чтобы найти объем цилиндра через диаметр и диагональ нужно представить высоту цилиндра в виде квадратного корня разности из квадратов диагонали и диаметра, а затем умножить это на площадь основания, состоящую из числа π и четверти квадрата диаметра.
V=(πD^2 h)/4=(πD^2 √(d^2-D^2 ))/4
Чтобы в цилиндр можно было вписать сферу, нужно чтобы диаметр цилиндра был равен его высоте, тогда сфера будет соприкасаться со всеми гранями цилиндра и ее радиус будет равен радиусу цилиндра, то есть половине его диаметра. (рис. 25.2)
r_1=r=D/2
Чтобы вокруг цилиндра можно было описать сферу, нужно точно так же чтобы диаметр цилиндра совпадал с высотой, и радиус описанной сферы будет равен половине диагонали цилиндра.
R=d/2
Примечание. Это урок с решениями задач по геометрии (раздел цилиндр). Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”.
Задача
Осевое сечение цилиндра – квадрат, диагональ которого равна 4√2.
Вычислить объем цилиндра.
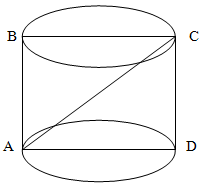
Решение.
Поскольку диагональ сечения цилиндра – квадрат, то обозначим его сторону как a.
a2 + a2 = (4√2)2
2a2 = 32
a2 = 16
a = 4
Объем цилиндра найдем по формуле:
V = πd2 / 4 * h
откуда
V = π42 / 4 * 4
V = 16π
Ответ: Объем цилиндра равен 16π
Задача
Куб с ребром длиной а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.
Решение.
Проведем плоскость через основание цилиндра.

Диагональ куба является одновременно диаметром цилиндра. Зная сторону куба, определяем длину диагонали AC квадрата ABCD как
CD2 + AD2= AC2
a2 + a2 = AC2
2a2 = AC
AC = a√2
Проведем плоскость через ось цилиндра по диагонали AC. Высота сечения равна длине ребра куба и по условиям задачи рана а, а ширина сечения равна a√2.
Таким образом, площадь сечения равна:
S = a * a√2 = a2√2
Ответ: a2√2
Задача
Диагональ осевого сечения цилиндра равна 12 см и образует с плоскостью нижнего основания угол 45 градусов. Найти обьём цилиндра.
Решение.
Поскольку основание осевого сечения образует с высотой цилиндра, принадлежащей сечению, прямой угол, то треугольник, который образован диагональю осевого сечения, высотой цилиндра и его диаметром – прямоугольный.
Исходя из этого, угол между диагональю и высотой также равен 45 градусов ( 180 – 90 – 45 ).
Таким образом, треугольник является равнобедренным, а, следовательно, высота цилиндра равна его диаметру. Применив теорему Пифагора, найдем их.
d2 + d2 = 122
2d2 = 144
d2 = 72
Теперь применим формулу объема цилиндра V = пd2 / 4 h
V = 72п / 4 * √72
V = 18п * √72
Ответ: 18п√72
Задача
|
Высота цилиндра 2м. Радиус основания 7м. В этот цилиндр наклонно вписан квадрат так, что все вершины его лежат на окружностях оснований. Найти сторону квадрата. |
Висота циліндра 2м. Радіус основи 7м. В цей циліндр похило вписаний квадрат так, що всі вершини його лежать на окружностях основ. Знайти сторону квадрата. |
Решение. Рiшення.
|
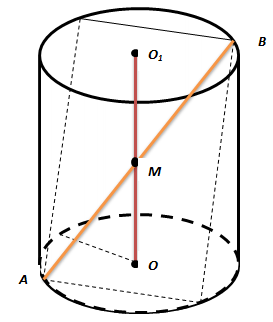
В силу симметричности квадрата и цилиндра и ввиду того, что квадрат наклонный, диагональ квадрата пересечет ось цилиндра ОО1 в точке М, являющейся серединой отрезкаОО1. По условию ОО1=2м, а ОА=7 м, поэтому ОМ=1м.
Пусть d – диагональ квадрата. Тогда сторона квадрата а равна: |
У силу симетричності квадрата і циліндра і зважаючи на те, що квадрат похилий, діагональ квадрата перетне вісь циліндра ОО1 в точці М, яка є серединою відрізка ОО1. За умовою ОО1=2м, а ОА=7 м, тому ОМ=1м.
Позначимо d – діагональ квадрата. Тоді сторона квадрата а: |
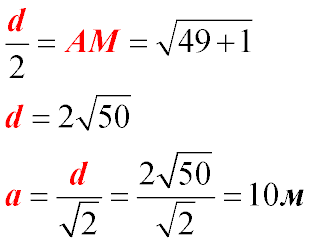
0
Цилиндр и его сечения |
Описание курса
| Диагональ цилиндра
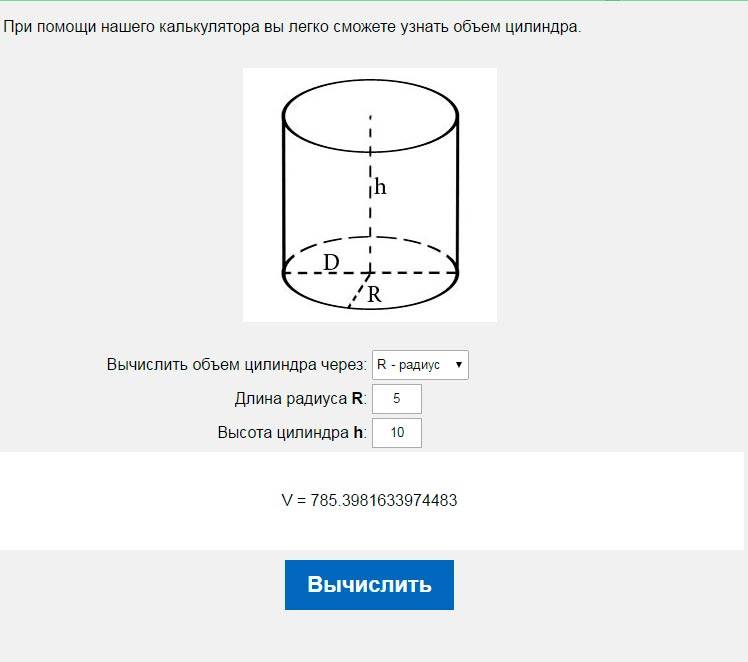
При помощи нашего калькулятора вы легко сможете узнать объем цилиндра. Так же если вам необходимо узнать объем бочки, круглой цистерны, круглого бака и т.д., то это калькулятор то, что Вам нужно.
|
|
|
| Вычислить объем цилиндра через: | |
| Длина радиуса R: | |
| Высота цилиндра h: |
Для того что бы вычислить объем цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить объем.
Объем цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
V=πR2h
- Если нам известен диаметр:
V=πD2/4h
Где V – объем, R – радиус, D – диаметр, h – высота, π – число Пи которое всегда примерно равно 3,14.
Расчет объема цилиндра |
 |