Всего: 42 1–20 | 21–40 | 41–42
Добавить в вариант
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 10 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 30 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 30 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
В бак цилиндрической формы, площадь основания которого равна 80 квадратным сантиметрам, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
В бак цилиндрической формы, площадь основания которого равна 90 квадратным сантиметрам, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
В бак цилиндрической формы, площадь основания которого равна 80 квадратным сантиметрам, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
В бак цилиндрической формы, площадь основания которого равна 60 квадратным сантиметрам, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы, налито 8 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы, налито 10 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,3 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В бак, имеющий форму правильной четырёхугольной призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В бак, имеющий форму правильной четырёхугольной призмы, налито 10 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,6 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 60 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 60 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 2,6 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В бак, имеющий форму правильной четырёхугольной призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 2 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 70 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 90 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 70 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
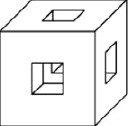
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Всего: 42 1–20 | 21–40 | 41–42
Найти объём заданной фигуры в принципе не сложно, если изначально есть информация о всех трёх необходимых размерах. То есть о длинне, о ширине и о высоте. Ведь ещё со школы всем известно, что именно перемножив данные размеры, мы и получим объём фигуры. В заданном вопросе присутствуют три различные сложные объёмны фигуры. Сложными их можно назвать потому, что они состоят и некоего количества маленьких кубиков.
Учитывая то, что благодаря заданному условию по объёму каждого маленького кубика,- получается возможным узнать необходимые нам размеры, – получается, что и объём этих трёх сложных фигур найти можно. Причём сделать это можно отталкиваясь от двух принципов. Первый это традиционное умножение размеров длинны, ширины и высоты. А второй это сложение общего количества маленьких кубиков в каждой сложной фигуре.
1) Решение задачи по первому варианту:
а) Длинна фигуры 5 кубиков, ширина 2 кубика, высота 2 кубика. И ходя из известных условий мы знаем, что длинна любого рёбра маленького кубика равна 1-му сантиметру. Умножаем соответственно 5 х 2 х 2. Получаем число 20. Значит объём этой фигуры равен 20 кубическим сантиметрам.
б) В этом примере все три размера одинаковы и составляют по 10 кубиков. Умножая 10 х 10 х 10 получаем число 1000. Ну и подставляя всё тот же один сантиметр получаем 1000 кубических сантиметров или просто один кубометр.
в) В третьем случае можно предположить, что целой сложная фигура будет тогда, когда крановщик закончит работу и уложит сверху последний пласт. В получившейся фигуре длинна и ширина будут равны,- по 10 кубиков, а высота получится 6 кубиков. Умножая 10 х 10 х 6, получаем число 600. Объём этой сложной фигуры равен 600 кубических сантиметров. Ну а если не считать верхний пласт, то конечно 500, поскольку в верхнем пласте маленьких кубиков ровно 100 штук. Ну и соответственно объём верхнего пласта равен 100 кубическим сантиметрам.
Ну а при использовании второго варианта нужно просто складывать общее количество объёмов маленьких кубиков в каждой фигуре. А так как для сложения можно использовать и умножение, то основной принцип никуда не денется. Только вместо линейных размеров длинны, ширины и высоты, будем складывать объёмы. И в итоге всё получится точно так же. В первом случае 20 маленьких кубиков по одному кубическому сантиметру каждый. В итоге сложения получим те же самые 20 кубических сантиметров. Во втором и в третьем случаях всё точно так же. Только учитывая количество маленьких кубиков в каждой сложной фигуре, чтобы узнать их количество будет проще применить умножение, чем сложение!
-
Расчет обЪема и веса детали
На рисунке 1
приведена схема разбивки детали на
элементарные объемы. Объем детали будет
равен алгебраической сумме элементарных
объемов.
Рисунок 1 – Схема
разбивки детали на элементарные объемы
Рассмотрим элемент,
объем которого мы можем найти по формуле
(1)
VΙ
= V1-VА-VВ–
VС-VД-VЕ-VЖ
VЗ ,
(1)
где
объем V1
– объем полого цилиндра:
Vпол.
цил. = 0,785 ∙
h
∙ (D2
– d2),
(2)
V1=0,785∙
34 ∙ (192,7762
– 972)=740743,22
мм3
объем VА
– объем четверти тора:
VА=2,47r2(D-0,848r),
(3)
VА=2,47∙102((97+20)-0,848∙10)=26804,44мм3
объем VВ
– объем
четверти тора:
VВ=2,47r2(D+0,848r),
(4)
VВ=2,47∙102((172-20)+0,848∙10)=39638,56мм3
объем VС
– объем полового цилиндра, находим по
формуле (2)
VС=0,785∙102(1522-1172)=
73907,75 мм3
объем VД
– объем
восьми отверстий, имеющих форму цилиндра:
Vцил.
= 0,785∙h∙D2,
(5)
VД=8∙0,785∙7∙92=3560,76
мм3
объем VЕ
– объем восьми отверстий, имеющих форму
усеченного конуса:
VЕ=

(6)
VЕ
=

объем Vж–
объем полового цилиндра, находим по
формуле (2)
Vж=0,785∙14(1752+1132)
= 6237,44 мм3
объем Vз
– объем четверти тора, находится по
формуле (4)
Vз
= 19596,58 мм3
VΙ
= 378228,20 мм3
Рассмотрим второй
элемент, объем которого мы можем найти
по формуле (6)
VΙΙ
= V2-VК-VИ
, (7)
где
объем V2–
объем цилиндра, находим по формуле (5)
V2
= 0,785∙972∙56=413619,64
мм3
объем VК–
объем цилиндра, находим по формуле (5)
VК
= 0,785∙772∙56=260638,84
мм3
объем VИ–
объем двух конических кольца:
VИ
= 0,524(3D-2d)dH
, (8)
VИ
= 2∙0,524(3∙97-2∙3,5)3,5∙11=11458,83 мм3
VΙΙ=141521,97
мм3
Рассмотрим третий
элемент объем, которого VΙΙΙ
– это объем зубьев колеса, и он равен
объему полого цилиндра (формула (2)),
умноженному на коэффициент, равный
0,55:
VΙΙΙ
=∙0,55 0,785∙34(210,782
– 192,782)
= 106655,70мм3,
(9)
Складывая объемы
трех этих элементов найденные по формулам
(1), (7), (9) получим объем всей детали:
VД
= VΙ+VΙΙ+VΙΙΙ ,
(10)
где
VД– объем детали;
VΙ
,VΙΙ,VΙΙΙ
– объемы,
получаемые по формулам (1,7,9).
VД=
626405,87 мм3
= 626,406 см3
Теперь, зная объем
детали, найдем массу детали по формуле
(11):
МД
= VД
∙ ρ,
(11)
где
ρ
– плотность материала,

г/см3.
МД
= 626,406 ∙ 7,8 = 4917,29 г
-
Определение группы металла , группы сложности , группы точности , исходного индекса
Расчет ведем по
ГОСТ 7505-89.
Группа стали
назначается, исходя из среднего массового
содержания углерода или легирующих
элементов. Материал – Cталь
20ХН3А ГОСТ 4543-71, суммарная массовая доля
легирующих элементов 4%, а значит группа
стали М2.
Степень сложности
определяется путем вычисления следующего
отношения
(11):
Сi
=

(12)
где
VПОК
– объем поковки;
VФ
– объем геометрической фигуры, в которую
вписывается форма детали (рисунок 2).
Рисунок 2 –
Геометрическая фигура, в которую
вписывается форма детали
Для
данной детали описанной фигурой будет
являться цилиндр, размеры которого
увеличены на 1,05. Найдем объем этого
цилиндра по формуле (2):
VФ
= 0,785 ∙ 58,8 ∙ 221,322
= 2260936,19 (мм3).
Объем
поковки на данном этапе находится по
формуле (13):
VПОК
= VД
∙
КР,
(13)
где
КР
– расчетный коэффициент, КР
= 1,7.
VПОК
=626405,87
∙ 1,7 = 1064889,97 (мм3).
Сi
=

По
расчету получаем степень сложности
поковки С2.
Класс
точности поковки устанавливается в
зависимости от технологического процесса
и оборудования для ее изготовления, а
также исходя из предъявляемых требований
к точности размеров поковки. Согласно
ГОСТ 7505-89 выбираем
4-й класс точности
– Т4.
Массу
поковки найдем по формуле, аналогичной
формуле (11):
МПОК
= 1064,889 ∙ 7,8 = 8306,1 г
Исходный
индекс для последующего назначения
основных припусков, допусков и допускаемых
отклонений определяется в зависимости
от массы, марки стали, степени сложности
и класса точности поковки по ГОСТ
7505-89.
В данном случае исходный индекс
14.
Объем
Сведения из теории
Объем прямоугольного параллелепипеда – V = abc.
Объем пирамиды – 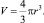
Объем прямого кругового цилиндра – V = 2πr2h.
Объем конуса – 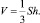
Объем шара – 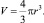
Задача 323. Сколько коробок в форме прямоугольного параллелепипеда размерами 30×40×50 (см) можно поместить в кузов машины размерами 2×3×1,5 (м)?
Ответ: 150.
Задача 324. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см×40 см?
Ответ: 90.
Задача 325. Размеры кирпича 25×12×6,5 (см). Найдите вес одного кирпича в граммах, если объемный вес кирпича равен 1700 кг/м3.
Ответ: 3315.
Задача 326. Какова должна быть площадь кабинета высотой 3,5 м для класса в 28 человек, если на каждого ученика нужно 7,5 м3 воздуха?
Ответ: 60.
Задача 327. Прямолинейный участок дороги шириной 10 м и длиной 100 м требуется покрыть асфальтом толщиной 5 см. Сколько потребуется машин асфальта, если объемный вес асфальта равен 2,4 т/м3, а грузоподъемность одной машины – 5 тонн?
Ответ: 24.
Задача 328. Пирамида Хеопса имеет форму правильной четырехугольной пирамиды, сторона основания которой равна 230 м, а высота около 138 м. Найдите ее объем в кубических метрах.
Ответ: 2433400.
Задача 329. В цилиндрический сосуд, в котором находится 6 дм3 воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали в кубических дециметрах?
Ответ: 3.
Задача 330. Воду, находящуюся в цилиндрическом сосуде на уровне 12 см, перелили в цилиндрический сосуд, в два раза большего диаметра. На какой высоте будет находиться уровень воды во втором сосуде?
Ответ: 3.
Задача 331. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Ответ: 1,125.
Задача 332. Воду, заполняющую всю коническую колбу высотой 12 см, перелили в цилиндрический сосуд, радиус основания которого равен радиусу окружности конической колбы. На какой высоте от основания цилиндрического сосуда будет находиться поверхность воды?
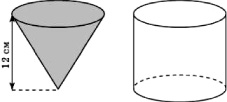
Задача 333. Медный прямоугольный параллелепипед, ребра которого равны 20 с, 20 см и 10 см, переплавлен в шар. Найдите радиус шара. (Примите π ≈ 3.)
Ответ: 10.
Задача 334. Сколько нужно взять медных шаров радиуса 2 см, чтобы из них можно было выплавить шар радиуса 6 см?
Ответ: 27.
Задача 335. Найдите радиус шара, который можно выплавить из трех медных шаров радиусов 3 см, 4 см и 5 см.
Ответ: 6.
Задача 336. Мякоть вишни окружает косточку толщиной, равной диаметру косточки. Считая шарообразной форму вишни и косточки, найдите отношение объема мякоти к объему косточки.
Ответ: 26.
Задача 337. Профиль русла реки имеет форму равнобедренной трапеции, основания которой равны 10 м и 6 м, а высота – 2 м. Скорость течения равна 1 м/с. Какой объем воды проходит через этот профиль за 1 мин? Ответ дайте в кубических метрах.
Ответ: 960.
Задача 338. Чугунная труба имеет длину 2 м и внешний диаметр 20 см. Толщина стенок трубы равна 2 см. Найдите вес трубы, если удельный вес чугуна примерно равен 7,5 г/см3. Ответ дайте в килограммах. (Примите π ≈ 3.)
Ответ: 162.
Задача 339. Какой объем краски потребуется, чтобы окрасить внешнюю поверхность цилиндрической трубы диаметра 1 м и длины 10 м слоем краски в 1 мм? Ответ дайте в кубических дециметрах. (Примите π ≈ 3.)
Ответ: 30.
Задача 340. Какой объем краски потребуется, чтобы окрасить поверхность шара радиуса 1 м слоем краски в 0,5 мм? Ответ дайте в кубических дециметрах. (Примите π ≈ 3.)
Ответ: 6.
Задача 341. Квадратный лист бумаги со стороной 6 см перегнули по пунктирным линиям, показанным на рисунке, и сложили треугольную пирамиду. Найдите ее объем.
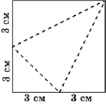
Ответ: 9.
Задача 342. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).
Ответ: 12.
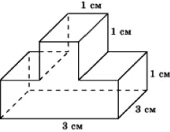
Задача 343. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).
Ответ: 40.
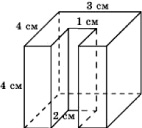
Задача 344. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).
Ответ: 12.
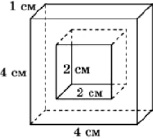
Задача 345. В каждой грани медного куба с ребром 6 см проделали сквозное квадратное отверстие со стороной квадрата 2 см. Найдите вес оставшейся части, считая удельный вес меди приблизительно равным 0,9 г/см3.
Ответ: 144.
Задача 346. Найдите объем детали, изображенной на рисунке, составленной из двух частей цилиндров. (При-
мите π ≈ 3).
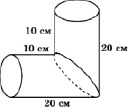
Ответ: 2250.
Задача 347. Найдите объем детали, изображенной на рисунке, вырезанной из цилиндра. (Примите π ≈ 3.)
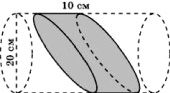
Ответ: 3000.
Задача 348. Диаметр Солнца примерно в 400 раз больше диаметра Луны. Во сколько раз объем Солнца больше объема Луны?
Ответ: 64000000.
Для определения объема детали необходимо найти объем тела, образованного этой деталью. Для этого можно воспользоваться формулами для объема простейших геометрических тел, таких как параллелепипед, цилиндр или шар.
Если форма детали не является простейшей, то ее объем можно разбить на более простые части и найти объем каждой из них, а затем сложить.
На первом фото дана деталь, форма которой напоминает цилиндр с полусферой сверху. Для определения объема необходимо найти объем цилиндра и объем полусферы, а затем сложить:
V = Vцилиндра + Vполусферы = πr²h + 2/3πr³/2
где r – радиус основания цилиндра и полусферы, h – высота цилиндра.
На втором фото дана деталь, форма которой напоминает параллелепипед с двумя вырезами. Объем такой детали можно найти как разность объема большого параллелепипеда и объемов двух меньших параллелепипедов:
V = Vбольшого параллелепипеда – 2Vмаленьких параллелепипедов = (a×b×h) – 2(a/2×b/2×h)
где a, b, h – соответственно длина, ширина и высота большого параллелепипеда.
На третьем фото дана деталь, форма которой напоминает тетраэдр. Объем такой детали можно найти по формуле для объема тетраэдра:
V = 1/3×Sоснования×h
где Sоснования – площадь основания тетраэдра, h – высота тетраэдра, опущенная на основание.


