Если кристалл кубической системы
обладает плотностью ρ (г/см3),
известен тип решетки (простая, объемно-
центрированная кубическая или
гранецентрированная[ кубическая), то
расчет производится следующим образом.
Число атомов, n необходимое
для построения данного куба (в таблице).
Масса куба определяется через массу
атомов (для металлов):
![]() ,
,
где А – атомная масса металла, N
– число Авогадро. Объем элементарной
ячейки определяется через плотность
ρ:
![]() .
.
Длина ребра куба определяется по формуле:
![]()
(см, м).
|
Таблица. Важнейшие характеристики |
То же, % |
52,4 |
68,0 |
74,0 |
34,0 |
74,0 |
|
Плотность упаковки |
π/6 |
(π√3)/8 |
(π√2)/6 |
(π√3)/16 |
(π√2)/6 |
|
|
Атомный радиус |
а√2 |
(а√3)/4 |
(а√2)/4 |
(а√3)/8 |
а/2 |
|
|
Число атомов
В элементарной |
1 |
2 |
4 |
8 |
2 |
|
|
Координаци-онное |
6 |
8 |
12 |
4 |
12 |
|
|
Характеристики |
Простой куб |
Объемно-центрированный |
Гранецентриро-ванный |
Решетка алмаза |
Гексагональная |
Пример. Определить длину ребра куба
элементарной кристаллической ячейки
металлического свинца, имеющего решетку
типа ГЦК и плотность 11340 кг/м3 .

a
Решение:
-
Изобразим элементарную кристаллическую
ячейку и обозначим длину ребра куба
(а). -
Находим n– число
частиц, необходимое и достаточное для
построения ячейки:
![]()
-
По формуле определяем длину ребра
куба.
![]()
![]()
-
Определяем атомный радиус свинца, по
его величине делаем вывод о физических
свойствах Pb.
![]()
-
Зная плотность свинца и число n
можно определить объем элементарной
ячейки:
![]()
-
Можно оценить, сколько молей Pb
содержится в 1 м3 твердого свинца. -
Оценить сколько атомов содержится в 1
м3 Pb. -
Сколько весит один атом Pb.
-
Рассчитать плотность упаковки и сделать
вывод.
1.3. Расчет энергии кристаллической решетки.
Под энергией решетки U
понимают ту энергию, которая выделяется
при образовании кристаллов из частиц,
составляющих решетку и находящихся в
свободном состоянии (состояние идеального
газа) при той же температуре.
Для ионных кристаллов такими частицами
являются ионы, для атомных – атомы и
т.д..
Значение U вычисляют
разными способами. Рассмотрим способ
расчета на основе кругового процесса
Борна – Габера для NaCl:
![]() ,
,
где ∆H0обр
– энтальпия образования NaCl
из элементарных натрия и хлора,
кДж/моль.
∆H0субл.
– энтальпия сублимации металлического
натрия, кДж/моль.
INa
–энергия ионизации натрия, кДж/моль.
Eсвязи – энергия
диссоциации связи Cl –
Cl, кДж/моль.
ECl –
энергия сродства атомов хлора к электрону,
кДж/моль.
U – энергия кристаллической
решетки NaCl, кДж/моль.
Необходимые справочные данные приведены
в приложении.
Капустинский А.Ф. предложил уравнение
для расчета энергии моля кристалла
имеющего ионную решетку:
![]()
(кДж/моль)
z1 и z2
– валентность ионов.
r1 и r2
– радиусы ионов для координационного
числа 6,Å
∑n – число ионов
в молекуле.
Необходимые справочные данные приведены
в таблицах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Определение параметров элементарной кристаллической ячейки в виде параллелепипеда с параметрами длины рёбер a, b, c и с углами между рёбрами
α, β, γ
Постоя́нная решётки, или параметр решётки — размеры элементарной кристаллической ячейки кристалла. В общем случае элементарная ячейка представляет собой параллелепипед с различными длинами рёбер, обычно эти длины обозначают как a, b, c. Но в некоторых частных случаях кристаллической структуры дли́ны этих рёбер совпадают. Если к тому же выходящие из одной вершины рёбра равны и взаимно перпендикулярны, то такую структуру называют кубической. Структуру с двумя равными рёбрами, находящимися под углом 120 градусов, и третьим ребром, перпендикулярным им, называют гексагональной.
Принято считать что, параметры элементарной ячейки описываются 6 числами: 3 длинами рёбер и 3 углами между рёбрами, принадлежащими одной вершине параллелепипеда.
Например, элементарная ячейка алмаза — кубическая и имеет параметр решётки 0,357 нм при температуре 300 К.
В литературе обычно не приводят все шесть параметров решётки, только среднюю длину рёбер ячейки и тип решётки.
Размерность параметров решётки a, b, c в СИ — длина. Величину, ввиду малости, обычно приводят в нанометрах или ангстремах (1 Å = 0,1 нм).
Параметры решётки могут быть экспериментально определены методами рентгеноструктурного анализа (исторически первый метод, развитый в начале XX века) или, начиная с конца XX века, — атомно-силовой микроскопией. Параметр кристаллической решётки может использоваться в качестве природного эталона длины нанометрового диапазона.[1][2]
Объём элементарной ячейки[править | править код]
Объём элементарной ячейки можно вычислить, зная её параметры (длины и углы параллелепипеда). Если три смежных ребра ячейки представить в виде векторов, то объём ячейки V равен (с точностью до знака) тройному скалярному произведению этих векторов (т.е. скалярному произведению одного из векторов на векторное произведение двух других). В общем случае
Для моноклинных решёток α = γ = 90°, и формула упрощается до
Для орторомбических, тетрагональных и кубических решёток угол β также равен 90°, поэтому[3]
Для тригональных (ромбоэдрических) решёток α = β = γ ≠ 90°, а также a = b = c, поэтому
Слоистые полупроводниковые гетероструктуры[править | править код]
Постоянство параметров решётки разнородных материалов позволяет получить слоистые, с толщиной слоёв в единицы нанометров сэндвичи разных полупроводников. Этот метод обеспечивает получение широкой запрещённой зоны во внутреннем слое полупроводника и используется при производстве высокоэффективных светодиодов и полупроводниковых лазеров.
Согласование параметров решётки[править | править код]
Параметры решётки важны при эпитаксиальном выращивании тонких монокристаллических слоёв другого материала на поверхности иного монокристалла — подложки. При значительной разнице параметров решётки материалов трудно получить монокристалличность и бездислокационность наращиваемого слоя. Например, в полупроводниковой технологии для выращивания эпитаксиальных слоёв монокристаллического кремния в качестве гетероподложки обычно используют сапфир (монокристалл оксида алюминия), так как оба имеют практически равные постоянные решётки, но с разным типом сингонии, у кремния — кубическая типа алмаза, у сапфира — тригональная.
Обыкновенно параметры решётки подложки и наращиваемого слоя выбирают так, чтобы обеспечить минимум напряжений в слое плёнки.
Другим способом согласования параметров решёток является метод формирования переходного слоя между плёнкой и подложкой, в котором параметр решётки изменяется плавно (например, через слой твёрдого раствора с постепенным замещением атомов вещества подложки атомами выращиваемой плёнки, так чтобы параметр решётки слоя твёрдого раствора у самой плёнки совпадал с этим параметром плёнки).
Например, слой фосфида индия-галлия с шириной запрещённой зоны 1,9 эВ может быть выращен на пластине арсенида галлия с помощью метода промежуточного слоя.
См. также[править | править код]
- Триклинная сингония
- Моноклинная сингония
- Ромбическая сингония
- Тетрагональная сингония
- Кубическая сингония
Примечания[править | править код]
- ↑ R. V. Lapshin. Automatic lateral calibration of tunneling microscope scanners (англ.) // Review of Scientific Instruments (англ.) (рус. : journal. — USA: AIP, 1998. — Vol. 69, no. 9. — P. 3268—3276. — ISSN 0034-6748. — doi:10.1063/1.1149091.
- ↑ R. V. Lapshin. Drift-insensitive distributed calibration of probe microscope scanner in nanometer range: Real mode (англ.) // Applied Surface Science : journal. — Netherlands: Elsevier B. V., 2019. — Vol. 470. — P. 1122—1129. — ISSN 0169-4332. — doi:10.1016/j.apsusc.2018.10.149.
- ↑ Dept. of Crystallography & Struc. Biol. CSIC. 4. Direct and reciprocal lattices (4 июня 2015). Дата обращения: 9 июня 2015. Архивировано 4 мая 2021 года.
Enter the unit cell mass (g) and the unit cell density (g/mm^3) into the Unit Cell Volume Calculator. The calculator will evaluate and display the Unit Cell Volume.
- All Volume Calculators
- Cell Density Calculator
- Grout Volume Calculator
- Powder Volume Calculator
Unit Cell Volume Formula
The following formula is used to calculate the Unit Cell Volume.
- Where UCV is the Unit Cell Volume (mm^3)
- UCM is the unit cell mass (g)
- UCD is the unit cell density (g/mm^3)
To calculate a unit cell volume, divide the unit cell mass by the unit cell density.
How to Calculate Unit Cell Volume?
The following example problems outline how to calculate Unit Cell Volume.
Example Problem #1:
- First, determine the unit cell mass (g).
- The unit cell mass (g) is given as: 5.
- Next, determine the unit cell density (g/mm^3).
- The unit cell density (g/mm^3) is provided as: 10.
- Finally, calculate the Unit Cell Volume using the equation above:
UCV = UCM / UCD
The values given above are inserted into the equation below:
UCV = 5 / 10 = .5 (mm^3)
Example Problem #2:
The variables needed for this problem are provided below:
unit cell mass (g) = 7
unit cell density (g/mm^3) = 2
Entering these values and solving gives:
UCV = UCM / UCD = 3.5(mm^3)
Объем элементарной ячейки Калькулятор
| Search | ||
| Дом | Химия ↺ | |
| Химия | Химия твердого тела ↺ | |
| Химия твердого тела | Объем различных кубических ячеек ↺ |
|
✖Длина ребра — это длина ребра элементарной ячейки.ⓘ Длина края [a] |
+10% -10% |
|
✖Объем — это количество пространства, которое занимает вещество или объект или которое заключено в контейнере.ⓘ Объем элементарной ячейки [VT] |
⎘ копия |
Объем элементарной ячейки Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Длина края: 100 Ангстрем –> 1E-08 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
1E-24 Кубический метр –> Конверсия не требуется
11 Объем различных кубических ячеек Калькуляторы
Объем элементарной ячейки формула
Объем = Длина края^3
VT = a^3
Что такое элементарная ячейка?
Наименьшая повторяющаяся единица кристаллической решетки – это элементарная ячейка, строительный блок кристалла. Все идентичные элементарные ячейки определены таким образом, что они заполняют пространство без перекрытия. Трехмерное расположение атомов, молекул или ионов внутри кристалла называется кристаллической решеткой. Он состоит из множества элементарных ячеек. Одна из трех составляющих частиц занимает каждую точку решетки.
Элементарная ячейка кристаллической решетки служит для описания микроструктуры материалов. От ее параметров зависят многие физико-химические свойства вещества: твердость, температура плавления, электро- и теплопроводность, пластичность и другие. Типы этих элементарных структур были описаны еще в 19 веке. Одной из разновидностей является примитивная ячейка. Для выделения в структуре материала элементарной ячейки необходимо соблюдение ряда условий.
Кристаллическая решетка
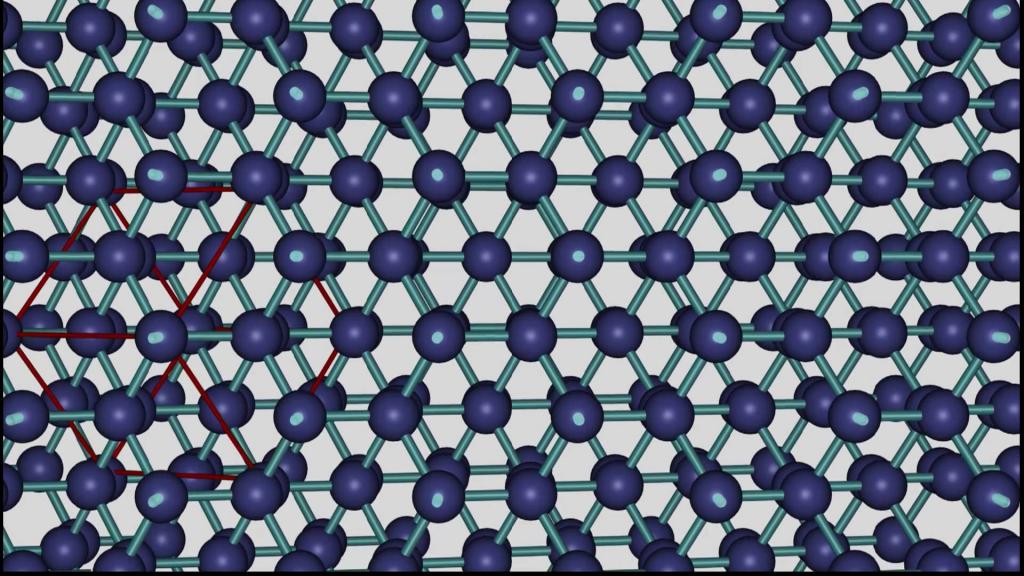
Все твердые тела по внутренней структуре можно классифицировать на две формы: аморфные и кристаллические. Отличительной особенностью последних является специфическая организованная структура частиц.
Кристаллическая решетка – это упрощенная трехмерная модель твердых кристаллов, которая используется для анализа их свойств в физике, химии, биологии, минералогии и других науках. Внешне она похожа на сетку. В ее узлах находятся атомы вещества. Данный массив точек имеет определенный, регулярно повторяющийся порядок, специфичный для каждого вида вещества.
Что такое элементарная ячейка?
Элементарная ячейка кристаллической решетки – это наименьшая часть твердого тела, которая позволяет охарактеризовать его свойства. Она служит основой решетки и дублируется в ней бесчисленное количество раз.
Данная модель используется для упрощения визуального описания внутреннего строения кристаллов. При этом применяется система из 3 кристаллографических координатных осей, которые отличаются от обычных ортогональных тем, что они являются конечными отрезками определенного размера. Углы между осями могут быть равны 90° или быть непрямыми.
Если плотно заполнить элементарными ячейками определенный объем, то можно получить идеальный монокристалл. На практике более распространены поликристаллы, состоящие из нескольких ограниченных в пространстве регулярных структур.
Виды
В науке выделяют 14 видов элементарных ячеек решеток, обладающих уникальной геометрией. Впервые их описал французский физик Огюст Бравэ в 1848 г. Этого ученого считают основателем кристаллографии.

Данные типы элементарных структур кристаллической решетки группируют в 7 категорий, называемых сингониями, в зависимости от соотношения длин сторон и равенства углов:
- кубическая;
- тетрагональная;
- орторомбическая;
- ромбоэдрическая;
- шестиугольная;
- триклинная.
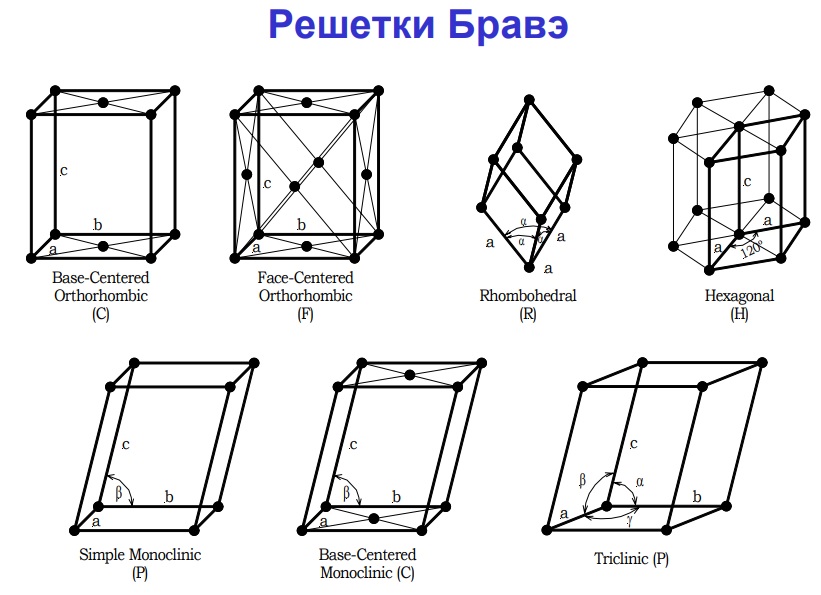
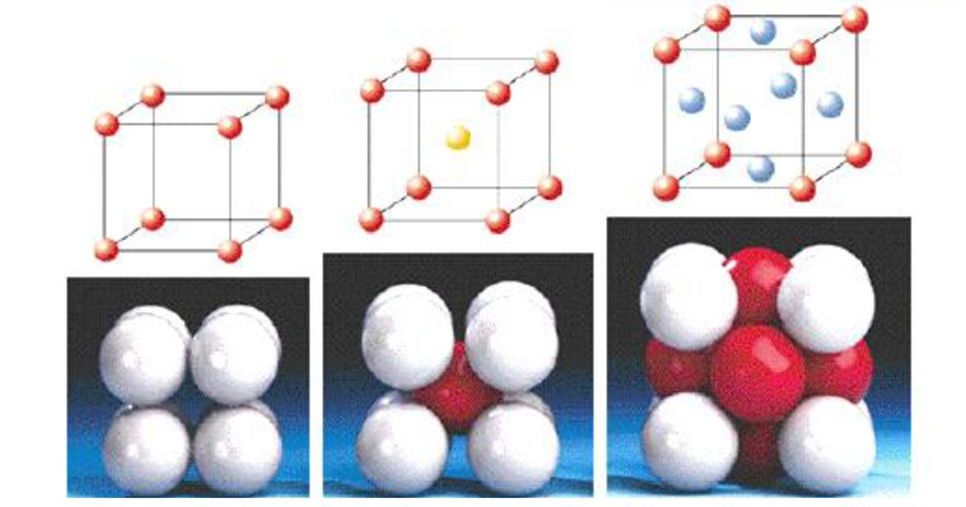
Наиболее простой и распространенной в природе из них является первая категория, которая в свою очередь делится на 3 типа решеток:
- Простая кубическая. Все частицы (а ими могут быть атомы, электрически заряженные частицы или молекулы) находятся в вершинах куба. Эти частицы идентичны. Каждой ячейке принадлежит 1 атом (8 вершин × 1/8 атома = 1).
- Объемноцентрированная кубическая. Отличается от предыдущей модели тем, что в центре куба находится еще одна частица. К каждой ячейке относится по 2 атома вещества.
- Гранецентрированная кубическая. Частицы содержатся в вершинах элементарной ячейки, а также в центре всех граней. Каждая из ячеек насчитывает по 4 атома.
Примитивная ячейка
Элементарная ячейка называется примитивной, если ее частицы находятся только в вершинах решетки и отсутствуют в других местах. Ее объем является минимальным по сравнению с другими типами. На практике она оказывается часто низкосимметричной (примером может служить ячейка Вигнера-Зейтца).
У не примитивных ячеек атом в центре объема делит их на 2 или на 4 одинаковые части. В гранецентрированной структуре происходит разделение на 8 частей. В металлографии пользуются понятием элементарной, а не примитивной ячейки, так как симметрия первой позволяет более полноценно описать кристаллическую структуру материала.
Признаки
Все 14 видов элементарных ячеек обладают общими свойствами:
- они являются простейшими повторяющимися структурами в кристалле;
- каждый центр решетки состоит из одной частицы, называемый узлом решетки;
- узлы ячейки соединяются между собой прямыми, которые формируют геометрию кристалла;
- противоположные грани параллельны;
- симметрия элементарной структуры соответствует симметрии всей кристаллической решетки.
При выборе структуры элементарной ячейки руководствуются некоторыми правилами. У нее должны быть:
- наименьший объем и площадь;
- наибольшее количество одинаковых ребер и углов между ними;
- прямые углы (по возможности);
- пространственная симметрия, отражающая симметрию всей кристаллической решетки.
Объем
Объем элементарной ячейки определяется в зависимости от ее геометрической формы. Для кубической сингонии он вычисляется как длина грани (межцентровое расстояние атомов), возведенная в третью степень. Для гексагональной сингонии объем можно определить по формуле, указанной ниже:
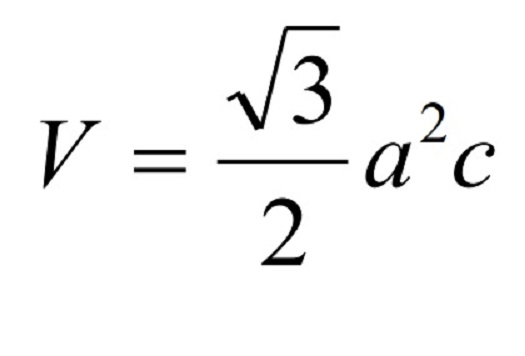
где a и c – параметры кристаллической решетки, измеряющиеся в ангстремах.
На практике параметры кристаллической решетки рассчитываются для того чтобы в дальнейшем можно было определить структуру соединения, массу атома (исходя из веса данного объема и числа Авогадро) или его радиус.




