Как найти объем эллипсоида через интеграл

Если объем тела V существует и функция S=S(x) является площадью сечения тела плоскостью (определенная и гладкая на промежутке [a;b]), каторая перпендикулярная к оси Ox в точке x, то объем тела находится за формулой
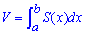Это достаточно простая зависимость определенного интеграла, проблема заключается в том, что функция площади не всегда выражается простой зависимостью. В этом Вы скоро убедится из готовых ответов на вычисление объема.
Примеры подобрано из программы для студентов мех-мата Львовского национального университета имени Ивана Франко. Студенты на практических занятиях имеют похожую программу учебы, задания в ряде случаев совпадают.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. “Практикум из математического анализа” (рядом стоит номер из сборника Б. П. Демидовича). 

Для изучения методики нахождения объема тел за известными сечениями основные этапы интегрирования повторяться из примера в пример.

Найти объемы тел, которые ограничены следующими поверхностями

Пример 2463 Найти объем эллипсоида

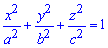
Вычисление: Сложим уравнение подинтегральной функции. В сечении тела плоскостью, что перпендикулярная к оси Ox, получим эллипс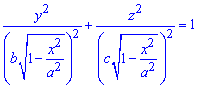

площадь которого выражается функцией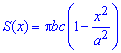

Определим пределы интегрирования:
у эллипсоида в канонической системе координат это промежуток [-a;a].
Найдем объем эллипсоида: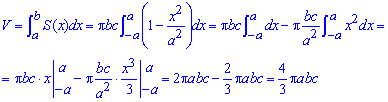

В том что формула справедлива можете убедиться, сопоставив вычисленную формулу с известной.
Объем фигур измеряется у кубических единиц !
Видим, если эллипсоид вырождается в сферу (a=b=c=R), то его объем равен V=4/3*Pi*R³ (формула известна из “школьной” геометрии).

Пример 2464 Найти объем тела 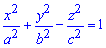(однополий гиперболоид).
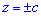Вычисление: Выражаем подинтегральную функцию.
В сечении тела плоскостью, что перпендикулярная к оси Ox, получим эллипс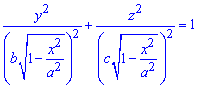

площадь которого выражается функцией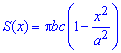

Определим пределы интегрирования : у эллипсоида в канонической системе координат это промежуток [- a;a].
Найдем объем эллипсоида :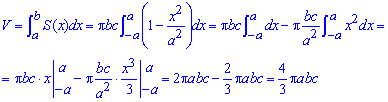

В том что формула справедливая можете убедиться, сравнив вычисленную формулу с известными в справочниках.
Объем фигур измеряется у кубических единиц !
Видим, если эллипсоид вырождается в сферу (a=b=c=R), то его объем равен V=4/3*Pi*R³ (формула известна из “школьной” геометрии).

Пример 2464Найти объем тела 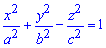(однополий гиперболоид).
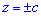Вычисление: Выражаемый подинтегральную функцию. В сечении тела плоскостью, что перпендикулярная к оси Oz, получим эллипс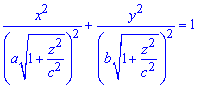

площадь которого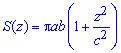

Пределы интегрирования известны за условием: .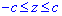
Кроме этого они являются подсказкой в каком направлении выполнять перерез и искать функцию площади.
Найдем объем однополого гиперболоида, что ограничен сверху и снизу плоскостями: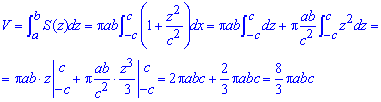

Определенный интеграл в этом задании находится без трудностей.

Пример 2465Найти объем тела образованного пересечением цилиндрических поверхностей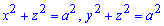
Вычисление: Сложим уравнение подинтегральной функции. Рассмотрим 1/8 часть тела (она расположена в И квадранте).
В сечении плоскостью, какая перпендикулярная к оси Oz, получим квадрат, площадь которого равна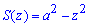

Пределы интегрирования : И вадрат прямоугольной системы координат [0;a].
Интегрированием вычисляем объем тела :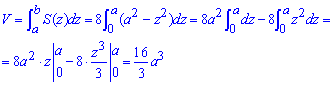

Как можно убедиться из формул площади, их интегрирования достаточно не сложное.

Пример 2468Вычислить объем тела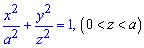
Вычисление: Выражаемый подинтегральную функцию. В сечении плоскостью, какая перпендикулярная к оси Oz, получим эллипс, площадь которого известна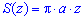
Пределы интегрирования за условием тоже известны:
.
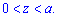Осталось проинтегрировать и подставить пределы.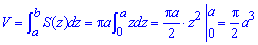

Получили, что объем тела равен V=Pi/2*a³ куб. од.

Пример 2469Найти объем тела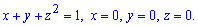
Вычисление: Запишем подинтегральную функцию. В сечении плоскостью, которая перпендикулярная к оси Oz, получим равнобедренный прямоугольный треугольник с катетом длиной 1-z², площадь которого легко находится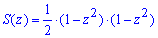

Пределы интегрирования : 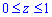(это видно из области существования функции ).
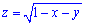Объем тела находим интегрированием: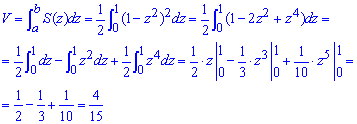

Из приведенных примеров Вы могли заметить, что все зависит от уравнения площади сечения. Для того, чтобы его записать нужно владеть добрым пространственным воображением и знать сечения основных пространственных тел. Все остальное зависит от Вашего умения интегрировать.

Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

Пусть требуется найти объем 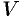тела, причем известны площади 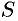сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси : , .

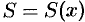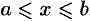Применим схему II (метод дифференциапа).

1. Через произвольную точку 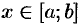проведем плоскость 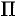, перпендикулярную оси (см. рис. 187). Обозначим через 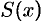площадь сечения тела этой плоскостью; 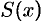считаем известной и непрерывно изменяющейся при изменении . Через 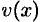обозначим объем части тела, лежащее левее плоскости 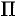. Будем считать, что на отрезке 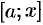величина 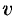есть функция от , т. е. .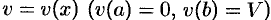

2. Находим дифференциал 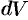функции 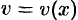. Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось в точках и 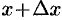, который приближенно может быть принят за цилиндр с основанием 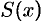и высотой 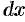. Поэтому дифференциал объема .

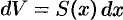3. Находим искомую величину 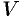путем интегрирования 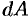в пределах от 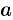до :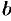

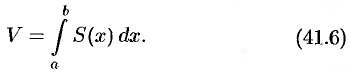
Полученная формула называется формулой объема тела по площади параллельных сечений.

Пример №41.6.

Найти объем эллипсоида .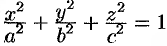

Решение:

Рассекая эллипсоид плоскостью, параллельной плоскости 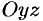и на расстоянии от нее 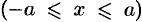, получим эллипс (см. рис. 188):

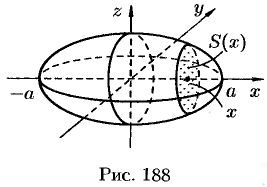
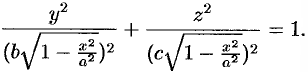
Площадь этого эллипса равна 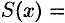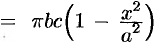. Поэтому, по формуле (41.6), имеем

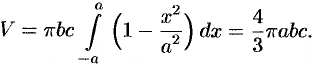
Объем тела вращения

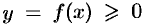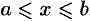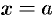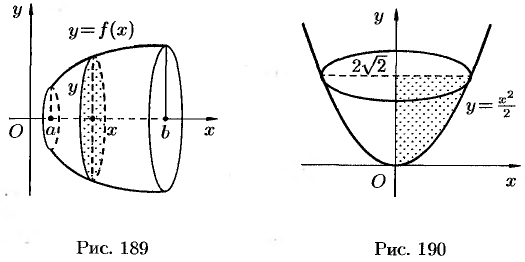
Пусть вокруг оси вращается криволинейная трапеция, ограниченная непрерывной линией , отрезком и прямыми и 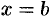(см. рис. 189). Полученная от вращения фигура, называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси , проведенной через произвольную точку оси (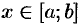), есть круг с радиусом 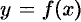. Следовательно, .

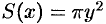Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком непрерывной функции 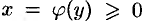и прямыми 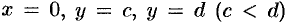, то объем тела, образованною вращением этой трапеции вокруг оси 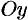, по аналогии с формулой (41.7), равен

Пример №41.7.

Найти объем тела, образованною вращением фигуры, ограниченной линиями 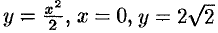вокруг оси 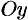(см. рис. 190).

Решение:

По формуле (41.8) находим:

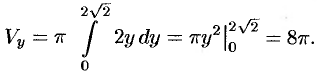
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Этот случай сводится
к теореме 2, если использовать формулы,
связывающие декартовы
и полярныекоординаты точки:

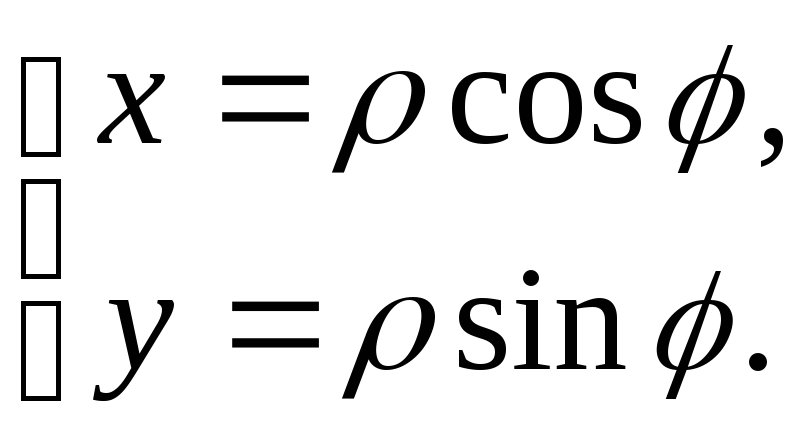
А.
.
Функция– непрерывно-диф-ференцируема. В этом
случае имеем:

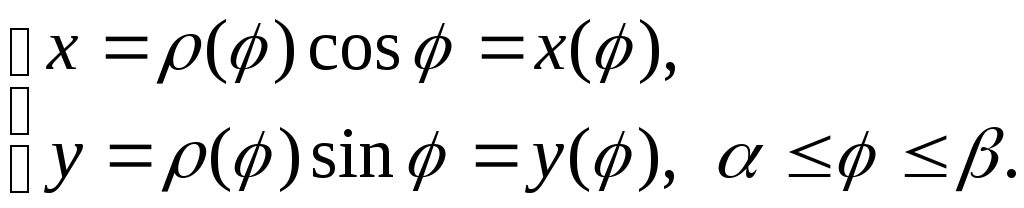
Вычисляем
производные, возводим их в квадрат и
складываем:

Итак, длина линии
в этом случае выражается формулой

Пример 4.
Вычислить длину части кардиоиды
расположенной вне окружности.

Решение.
Решим сначала неравенство

.

Итак, требуемая
часть кардиоиды соответствует изменению
отдо– это пределы интегрирования в формуле
(3). Проведем теперь предварительные
вычисления:

Т.к.
,
тои;
на этом промежутке синус положителен.

Вычисляем длину:

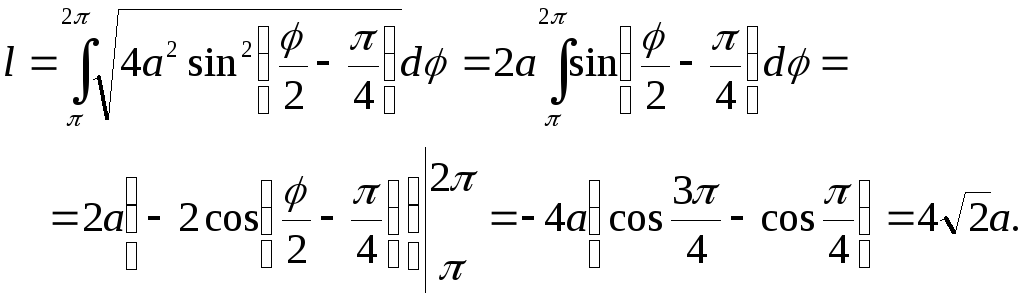
Предлагаем студентам
самостоятельно рассмотреть еще 2 случая
и получить нужные формулы:

В.
–

С.

–

Задачи
(для самостоятельного решения)

1. Вычислить длину
графика функций
.

2. Вычислить длину
петли линии
.

3. Вычислить длину
всей линии
.

4. Найти радиус
окружности, которая делит дугу астроиды

на три равновеликие части.

5. Найти длину всей
линии
.

6. Найти длину дуги
линии
.

7. Найти длину дуги
линии
.

§4. Вычисление объёмов некоторых тел

I Понятие объёма тела. Объём цилиндра

Понятие объёма
тела вводится аналогично понятию площади
плоской фигуры: в данное тело вписывают
многогранники
и описывают вокруг тела.
Их объёмы обозначими.

Определение
1. Пусть
для данного тела
существуют две после-довательности
многогранниковитаких, что.
Если,
то телоназывают кубируемым, а число– его объёмом.

Как и в случае
фигур, будем вписывать и описывать не
многогранники, а другие тела (и наборы
их), кубируемость которых уже доказана.

Дадим определение
цилиндра и докажем его кубируемость.

Пусть в некоторой
плоскости
дана линияи пусть дана прямая, перпендикулярнаяи проходящая через точку.
Поверхность, образованная движением
прямой,
когда в точкепробегает линию,
называют цилиндрической поверхностью.
При этом прямуюназывают образующей, а линию– направляющей поверхности.

Определение
2. Цилиндром
называют тело, ограниченное цилинд-рической
поверхностью с замкнутой направляющей
и двумя плоскостями, перпендикулярными
образующей. Части этих плоскостей,
высекаемые цилиндрической поверхностью,
называют основаниями цилиндра, а
расстояние между ними его высотой.

Лемма.
Цилиндр кубируем, если его основание
квадрируемо; его объём равен произведению
площади основания на высоту.

Доказательство.
Пусть
– высота, аоснование цилиндра ии– многоугольники такие, чтои.
Построим прямые призмы, основаниями
которых являютсяи.
Эти призмы будут вписанными и описанными
многогранниками. Из элементарной
геометрии известно, что объём призмы
равен произведению площади основания
на высоту. А так как площади оснований
(вписанных и описанных) – имеют равные
пределы, то и объёмы многогранников
будут иметь равные пределы. Это и означает
кубируемость цилиндра.

II Вычисление объёма тела по его поперечным сечениям

Теорема 1.
Пусть для данного тела известны площади
сечений, перпендикулярных некоторому
направлению, принятому за ось .
Тогда объём тела выражается формулой

(1)

где
– площадь сечения с абсциссойx,
a
и b
– абсциссы крайних сечений тела
(предполагается, что функция
– непрерывна).

Идея
доказательства.
Отрезок
разобьём на части точкамии, проведя плоскости,
разложим тело на слои. Рассмотримk-й
слой, расположенный между плоскостями
и.
На промежуткенепрерывная функциядостигает своего наименьшего и наибольшего
значений:исоответственно. Если на этих, наименьшем
и наибольшем сечениях построить цилиндры
с высотой,
то меньший цилиндр будет содержаться
вk-м
слое тела, а больший содержать в себе
этот слой. Наборы этих цилиндров
и дадут вписанные и описанные кубируемые
тела. Объёмы этих тел, очевидно, равны:

и
.

Но эти суммы – это
интегральные суммы для функции
,
которые стремятся к единому пределу –Теорема доказана.

Пример
1. Найти
объём эллипсоида

Решение.
Сечение эллипсоида плоскостью
– это эллипс

Его полуоси равны

и,
а площадь.
Итак, функция,
о которой идет речь в теореме 1, имеет
вид

и объём эллипсоида
дается интегралом

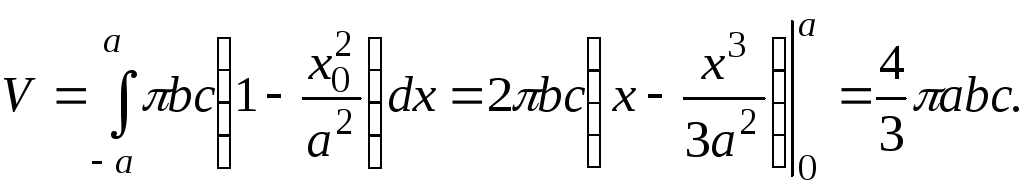
Пример
2. Найти
объём «цилиндрического отрезка», т.е.
части кругового цилиндра, отсекаемой
плоскостью, которая проходит через
диаметр основания.

Решение.
Пусть основания цилиндра – это круг
,
секущая плоскость проходит через ось
ординат и составляет уголс плоскостью основания – её уравнение.
Через точкупроведем плоскость, перпендикулярную
оси абсцисс. В сечении получим
прямоугольник. Его основание – хорда
круга, отстоящая от его центра на
расстоянии.
Её длина равна.
Высота прямоугольника – отрезок
образующей цилиндра между его основанием
и секущей плоскостью. Его длина.
Итак, площадь сечения с абсциссойимеет вид,
а искомый объём получим проинтегрировавпо промежутку:

Этот результат
можно записать в форме
,
где
– высота «цилиндрического отрезка».

Соседние файлы в папке MATANALIZ – 2

• #
• #
• #
• #
• #

Since I don’t know how much calculus you know, with a little intuition, you know all you really need to know if you just have some basic knowledge of integration, and substitution.

Consider the ellipse $$ frac{x^2}{a^2} + frac{y^2}{b^2} = 1$$ we have in particular $$ y = b sqrt{1 – frac{x^2}{a^2}}$$ so in particular the area of this ellipse is simply $$ A = 4int_0^a b sqrt{1 – frac{x^2}{a^2}} text{d}x $$ making the substitution $$ u = frac{x}{a} $$ we have $$ x = au Rightarrow text{d}x = a text{d}u$$ we get the area $$ A = 4ab int_0^1 sqrt{1-u^2} text{d}u $$ we now substitute $$ u = sin theta$$ so that $$text{d}u = cos theta text{d}theta $$ and we get $$ A = 4ab int_0^{pi/2} cos^2 theta text{d}theta $$ using the Pythagorean identity. With the substitution again $$ phi = frac{pi}{2} – theta$$ we get $$ A = – 4ab int_{frac{pi}{2}}^0 cos^2left( frac{pi}{2} – phiright) text{d}phi$$ adding these two expressions together, we get $$ 2A = (4ab) left(int_0^frac{pi}{2} cos^2(theta) text{d}theta + int_0^frac{pi}{2} sin^2(theta) text{d}theta right) = 4abint_{0}^{frac{pi}{2}} text{d}theta = 2pi ab Rightarrow A = pi ab$$

Okay, so the area of an ellipse is $pi ab$, where $a$ and $b$ are the lengths of the semi-minor and semi-major axes. Equipped with the formula, we’re going to use a double integral to find the volume, with the knowledge of how the inner integral evaluate, if you know what that means. If not, that’s totally fine, because you don’t really need that to understand what’s going on. Really, if we continuously add up all of the areas of all of the little ellipses we get slicing along the $x$ axis as we go along the ellipsoid, we get the area of the ellipsoid. So if we have the ellipsoid $$ frac{x^2}{a^2} + frac{y^2}{b^2} + frac{z^2}{c^2} = 1$$ If we pick some $x in [-a^2, a^2]$, we get the $y$–$z$ trace $$ frac{y^2}{displaystyleleft(b sqrt{1-frac{x^2}{a^2}} right)^2} + frac{z^2}{displaystyleleft(c sqrt{1-frac{x^2}{a^2}} right)^2} = 1$$ well, we recognize that as an ellipse, just like above. So, it’s area is just $$ pi left(b sqrt{1-frac{x^2}{a^2}} right) left(c sqrt{1-frac{x^2}{a^2}} right) = pi bc left( 1 – frac{x^2}{a^2}right) $$ and if we add up all of these little areas over all of our values of $x$, we get the volume of the ellipsoid. This is just the integral $$ V = int_{-a}^{a} pi b c left( 1 – frac{x^2}{a^2} right) text{d}x$$ we now can make the substitution $$ u = frac{x}{a}$$ when we have again that $$ text{d}x = a text{d}u $$ so that our volume becomes $$ V = pi abc int_{-1}^{1} 1 – u^2 text{d}u $$ we can just compute the anti-derivative using the inverse of the power rule to get $$ pi abc left. left[ u – frac{u^3}{3} right] right|_{-1}^{1} = pi abc left[ frac{2}{3} – left(- frac{2}{3} right) right] = frac{4}{3}pi abc$$ So the volume of this ellipsoid is just $$boxed{frac{4}{3}pi abc} $$

Понятие эллипсоида

Эллипсоид можно получить путем деформации сферы. Проще говоря, эллипсоид — это вытянутая либо сплюснутая сфера.

Онлайн-калькулятор объема эллипсоида

Эллипсоид обладает полуосями. Исходя из того, что эллипсоид — пространственное тело, то полуосей у него будет ровно на единицу больше, чем у эллипса, то есть, три.

Каноническое уравнение эллипсоида может быть записано так:

x2a2+y2b2+z2c2=1frac{x^2}{a^2}+frac{y^2}{b^2}+frac{z^2}{c^2}=1,

где a,b,ca, b, c — полуоси эллипсоида;
x,y,zx, y, z — координаты точек, принадлежащих эллипсоиду.

Полуоси эллипсоида – это положительные величины:

a>0,b>0,c>0a>0, b>0, c>0

Если:

a>b>ca>b>c,

то aa — это большая полуось, bb — средняя, а cc — малая.

Формула объема эллипсоида через его полуоси

Для вычисления объема эллипсоида существует такая формула:

Формула объема эллипсоида через его полуоси

V=43⋅π⋅a⋅b⋅cV=frac{4}{3}cdotpicdot acdot bcdot c

Полезно заметить, что эта формула переходит в формулу для объема шара, если положить:

a=b=c=Ra=b=c=R,

где RR — объем данного шара.

Рассмотрим несколько примеров.

Задача 1

Даны полуоси эллипсоида, численно равные 3 см3text{ см}, 4 см4text{ см}, 5 см5text{ см}. Определите его объем.

Решение

a=3a=3
b=4b=4
c=5c=5

По формуле вычисляем:

V=43⋅π⋅a⋅b⋅c=43⋅π⋅3⋅4⋅5≈251.2 см3V=frac{4}{3}cdotpicdot acdot bcdot c=frac{4}{3}cdotpicdot 3cdot 4cdot 5approx251.2text{ см}^3

Ответ

251.2 см3.251.2text{ см}^3.

Задача 2

Даны две полуоси эллипсоида – 6 см6text{ см} и 8 см8text{ см}. Найдите его объем, если известно, что третья полуось равна длине гипотенузы треугольника, катетами которого являются две вышеописанные полуоси.

Решение

Неважно, как обозначить данные полуоси, поэтому пусть:

b=8b=8
c=6c=6

Для нахождение неизвестной полуоси эллипсоида воспользуемся теоремой Пифагора для прямоугольного треугольника. По условию задачи, неизвестная полуось aa является гипотенузой прямоугольного треугольника, а полуоси bb и cc выступают катетами этого треугольника. Тогда:

a2=b2+c2a^2=b^2+c^2

a2=82+62a^2=8^2+6^2

a2=64+36a^2=64+36

a2=100a^2=100

a=10a=10

Теперь найдем объем эллипсоида по формуле:

V=43⋅π⋅a⋅b⋅c=43⋅π⋅10⋅8⋅6≈2009.6 см3V=frac{4}{3}cdotpicdot acdot bcdot c=frac{4}{3}cdotpicdot 10cdot 8cdot 6approx2009.6text{ см}^3

Ответ

2009.6 см3.2009.6text{ см}^3.

Не знаете, где можно заказать контрольную работу? Наши эксперты окажут вам оперативную помощь в решении контрольных работ по объемам фигур!

Тест по теме “Объем эллипсоида”