Физика.Как найти объём, если известна плотность вещества
Нося
Ученик
(86),
закрыт
11 лет назад
Как найти объём, если известна плотность вещества
Дополнен 13 лет назад
масса не известна
Лучший ответ
Жанна Мурзина
Знаток
(484)
13 лет назад
Масса равна объем * плотность, значитобъем равен масса / плотность
Остальные ответы
Angelina
Мастер
(1707)
13 лет назад
V=m/p (масса / плотность)
Ольга Цыкалова
Гуру
(3567)
13 лет назад
массу поделить на плотность
Vindigo
Мастер
(1793)
13 лет назад
p=m/v где p-плотность, кг/м3, m – масса тела, кг, V – объем тела, м3
Объем находится по формуле V=m/p
Лиечка
Профи
(905)
13 лет назад
масса/плотность
прими что нибудь за х
лина козленко
Знаток
(271)
5 лет назад
Массу делить на плотность
Григорий Коротаев
Ученик
(223)
5 лет назад
Масса не известна дебилы!
Найти массу, плотность или объем онлайн
На данной странице калькулятор поможет найти плотность, массу или объем вещества онлайн. Для расчета введите значения в калькулятор.
Объем, масса и плотность
Найти
Масса:
Объем:
Плотность:
Ответы:
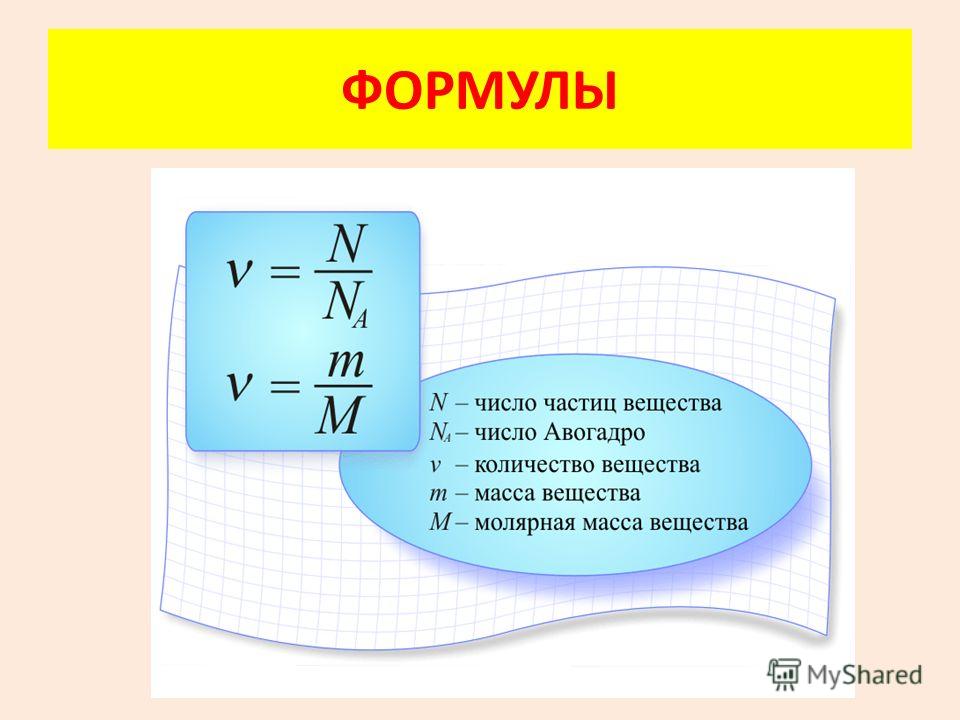
Формула для нахождения массы тела через плотность и объем:
m – масса; V – объем; p – плотность.
Формула для нахождения объема тела через плотность и массу:
m – масса; V – объем; p – плотность.
Формула для нахождения плотности тела через объем и массу:
m – масса; V – объем; p – плотность.
Калькулятор
Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
§ 3 Важно запомнить
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
На прошлом уроке мы познакомились с определением плотности тела, узнали формулу, по которой можно ее рассчитать: $rho = frac{m}{V}$.
Сейчас нам предстоит взглянуть на эту формулу с других сторон. Мы научимся находить объем и массу по известной плотности материала тела, решать задачи, используя полученные знания.
Расчет массы тела по его плотности
Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение — так они могут рассчитать массу будущего механизма или строения.
Как вычисляется масса тела по его плотности и объему?
Плотность определяется по формуле $rho = frac{m}{V}$. Выразим отсюда массу:
$m = rho V$.
Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.
Задача на расчет массы
Рассмотрим пример задачи на расчет массы.
Рассчитайте массу детали, изготовленной из латуни, объемом $0.15 space м^3$.
Из таблицы 1 предыдущего урока берем значение плотности латуни. Она равна $8500 frac{кг}{м^3}$.
Дано:
$rho = 8500 frac{кг}{м^3}$
$V = 0.15 space м^3$
$m -?$
Показать решение и ответ
Скрыть
Решение:
$m = rho cdot V$,
$m = 8500 frac{кг}{м^3} cdot 0.15 space м^3 = 1275 space кг approx 1.3 space т$.
Ответ: $m = 1275 space кг approx 1.3 space т$.
Расчет объема тела по его плотности
По какой формуле можно определить объем тела?
Подобным образом выразим из формулы плотности объем:
$V = frac{m}{rho}$.
Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.
Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.
Задача на расчет объема
Рассмотрим пример задачи на расчет объема.
Молоко в бутылке имеет массу $1.03 space кг$. Рассчитайте объем бутылки.
В таблице 2 прошлого параграфа находим молоко: его плотность равна $1030 frac{кг}{м^3}$.
Дано:
$rho = 1030 frac{кг}{м^3}$
$m = 1.03 space кг$
$V -?$
Решение:
$V = frac{m}{rho}$,
$V = frac{1.03 space кг}{1030 frac{кг}{м^3}} = 0.001 space м^3 = 1 space л$.
Ответ: $V = 1 space л$.
Дополнительные задачи
Задача №1
На рисунке 1 изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Масса одного куска 200 г. Масса брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Обозначим стороны упаковки как $a, b space и space с$, массу куска была $m_м$, массу куска мыла в упаковке — $m$, а общую массу мыла в упаковке — $m_{уп}$.
Объем куска мыла будем обозначать как $V_м$, а вместе с упаковкой — $V$.
Дано:
$a = 6 space см$
$b = 9 space см$
$c = 5.5 space см$
$m_м = 200 space г$
$m = 211 space г$
$V_м -?$
Показать решение и ответ
Срыть
Решение:
Найдем массу упаковки:
$m_{уп} = m — m_м$,
$m_{уп} = 211 space г — 200 space г = 11 space г$.
Общий объем упаковки и мыла:
$V = a cdot b cdot c$,
$V = 6 space см cdot 9 space см cdot 5.5 space см = 297 space см^3$.
Указано, что упаковка изготовлена из полиэтилена (из таблицы 1 предыдущего параграфа его плотность $rho_п$ равна $0.92 frac{г}{см^3}$).
Найдем объем упаковки $V_{уп}$:
$V_{уп} = frac{m_{уп}}{rho_{уп}}$,
$V_{уп} = frac{11 space г}{0.92 frac{г}{см^3}} approx 12 space см^3$.
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:
$V_м = V — V_{уп}$,
$V_м = 297 space см^3 — 12 space см^3 = 285 space см^3$.
Выразим в СИ:
$285 space см^3 = 285 cdot 1 space см cdot 1 space см cdot 1 space см = 285 cdot 0.01 space м cdot 0.01 space м cdot 0.01 space м = 285 cdot 0.000001 space м^3 = 0.000285 space м^3$.
Ответ: $V_м = 0.000285 space м^3$
Задача №2
Масса чугунного шара составляет 800 г. Его объем — $125 space см^3$. Будет ли этот шар сплошным (отлитым полностью из одного материала) или полым (иметь пространство внутри, заполненное, например, воздухом)?
Показать решение
Скрыть
Проверить это достаточно просто: рассчитаем плотность этого шара:
$rho = frac{m}{V}$,
$rho = frac{800 г}{125 space см^3} = 6.4 frac{г}{см^3}$.
Сравним полученное значение с табличной плотностью чугуна:
$rho = 7 frac{г}{см^3}$
Сколько бы тогда весил сплошной шар?
$m = rho V$,
$m = 7 frac{г}{см^3} cdot 125 space см^3 = 875 space г$.
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
Задача №3
В грузовой автомобиль загрузили 48 сосновых бревен. Масса каждого соснового бревна составляет $20 space дм^3$. На сколько увеличилась масса автомобиля после загрузки?
Из таблицы 1 предыдущего параграфа возьмем плотность сухой сосны ($400 frac{кг}{м^3}$). Переведем $20 space дм^3$ в $м^3$:
$20 space дм^3 = 20 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 20 cdot 0.001 space м^3 = 0.02 space м^3$.
Количество брусков — $n$.
Дано:
$V = 20 space дм^3$
$rho = 400 frac{кг}{м^3}$
$n = 48$
СИ:
$V = 0.02 space м^3$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем массу одного соснового бревна:
$m = rho cdot V$,
$m = 400 frac{кг}{м^3} cdot 0.02 space м^3 = 8 space кг$.
Масса всех сосновых бревен (M) будет равна:
$M = n cdot m$,
$M = 48 cdot 8 space кг = 384 space кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Упражнения
Упражнение №1
Какова масса $0.5 space л$ спирта, молока, ртути?
Дано:
$V = 0.5 space л$
$rho_1 = 800 frac{кг}{м^3}$
$rho_2 = 1030 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-4} space м^3$
$m_1 — ?$
$m_2 — ?$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Зная объем и плотность тела, мы может рассчитать его массу по формуле: $m = rho V$.
Рассчитаем массу спирта:
$m_1 = rho_1 V$,
$m_1 = 800 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.4 space кг$.
Рассчитаем массу молока:
$m_2 = rho_2 V$,
$m_2 = 1030 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.515 space кг$.
Рассчитаем массу ртути:
$m_3 = rho_3 V$,
$m_3 = 13600 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 6.8 space кг$.
Ответ: $m_1 = 0.4 space кг$, $m_2 = 0.515 space кг$, $m_3 = 6.8 space кг$.
Упражнение №2
Определите объем льдинки, масса которой $108 space г$.
Дано:
$m = 108 space г$
$rho = 900 frac{кг}{м^3}$
СИ:
$m = 0.108 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность льда, рассчитаем его объем:
$V = frac{m}{rho}$,
$V = frac{0.108 space кг}{900 frac{кг}{м^3}} = 0.00012 space м^3 = 120 space см^3$.
Ответ: $V = 120 space см^3$.
Упражнение №3
Сколько килограммов керосина входит в пятилитровую бутыль?
Дано:
$V = 5 space л$
$rho = 800 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Зная плотность и объем, найдем массу керосина:
$m = rho V$,
$m = 800 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 4 space кг$.
Ответ: $m = 4 space кг$.
Упражнение №4
Грузоподъемность лифта составляет $3 space т$. Сколько листов железа можно погрузить в лифт, если длина каждого листа равна $3 space м$, ширина — $60 space см$ и толщина — $4 space мм$?
Дано:
$M = 3 space т$
$a = 60 space см$
$b = 4 space мм$
$c = 3 space м$
$rho = 7800 frac{кг}{м^3}$
СИ:
$M = 3000 space кг$
$a = 0.6 space м$
$b = 0.004 space м$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем массу одного железного листа. Для этого нам нужно знать его объем (плотность мы взяли из таблицы). Объем мы может вычислить, перемножив друг на друга ширину, высоту и длину: $V = a cdot b cdot c$.
Масса железного листа:
$m = rho V = rho cdot a cdot b cdot c$,
$m = 7800 frac{кг}{м^3} cdot 0.6 space м cdot 0.004 space м cdot 3 space м = 56.16 space кг$.
Теперь разделим грузоподъемность лифта на массу одного лифта. Полученное целое число и будет ответом на вопрос задачи:
$n = frac{M}{m}$,
$n = frac{3000 space кг}{56.16 space кг} approx 53$.
Ответ: $n = 53$.
Упражнение №5
Кружка доверху наполнена молоком. Определите объем кружки, если масса молока в кружке $515 space г$, плотность молока найдите в таблице.
Дано:
$m = 515 space г$
$rho = 1030 frac{кг}{м^3}$
СИ:
$m = 0.515 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность молока, найдем объем, который оно занимает в кружке:
$V = frac{m}{rho}$,
$V = frac{0.515 space кг}{1030 frac{кг}{м^3}} = 0.0005 space м^3 = 0.5 space л$.
Ответ: $V = 0.5 space л$.
Задание
Возьмите баночку из-под меда. Рассмотрите внимательно этикетку. Найдите на ней, какова масса меда и объем баночки. Затем рассчитайте плотность меда. Полученный результат проверьте по таблице.
Дано:
$m = 800 space г$
$V = 500 space мл$
СИ:
$m = 0.8 space кг$
$V = 0.0005 space м^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем плотность меда:
$rho = frac{m}{V}$,
$rho = frac{0.8 space кг}{0.0005 space м^3} = 1600 frac{кг}{м^3}$.
По таблице плотность меда составляет $1350 frac{кг}{м^3}$. Существует множество различных сортов меда, плотность которых отличается друг от друга. Наше значение плотности не сильно отличается от табличного, поэтому можно сказать, что результат получен правильный.
Ответ: $rho = 1600 frac{кг}{м^3}$.
3}
Найти объем через
радиусдиаметрдлину окружностиплощадь поверхности
Радиус R
ммсмдммкмдюймы (in)футы (ft)
Результат в
кубические миллиметры (мм³)кубические сантиметры (см³)кубические дециметры (дм³)кубические метры (м³)кубические километры (км³)микролитры (мкл)миллилитры (мл)сентилитры (cl)децилитры (dl)декалитрылитры (л)столовая ложка (15мл)десертная ложка (10мл)чайная ложка (5мл)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности.
3
И снова в проверке ответа нам поможет калькулятор .
Конспект урока по теме «Плотность вещества. Косвенное измерение плотности вещества». 7 класс
Тема урока: «Плотность вещества. Косвенное измерение плотности вещества»
Цели урока.
Формирование
– представления о плотности вещества.
– знания формулы для расчета плотности вещества.
– умения анализировать связь между величинами, входящими в формулу.
– умения решать задачи с применением новых формул.
Развитие
– умения анализировать ситуацию,
– умения сравнивать результаты исследований,
– умения обобщать полученные данные,
– внимания, творческих способностей,
– умения работать в группах.
Воспитывать отношение к физике как элементу общечеловеческой культуры.
Оборудование.
- Доска с мелом.
-
Таблички с набором магнитов для фиксирования на доске.
- Презентация с заданиями на закрепление.
- Набор для лабораторных исследований: весы с разновесами, три тела раной массы и одинакового объема.
Ход урока
- Мотивация к учебной деятельности
«… Мир слишком удивителен, чтобы сидеть сложа руки». Ричард Бренсон, английский предприниматель и инвестор.
Учитель: Как вы понимаете эту фразу? (ответы учеников)
Эти слова известного английского предпринимателя Р.Бренсона будут эпиграфом нашего урока. Сегодня вам предстоит, используя накопленный багаж знаний, открыть для себя новые знания. Что для этого необходимо?
Ученики: Надо попробовать сделать что-то новое, и если нам не хватает нашего багажа знаний, попробовать найти пути решения получения новой информации, новых знаний, и пойти по выбранному пути.
- Актуализация знаний.
Учитель: С чего начинается изучение нового материала на любом уроке?
Ученики: С повторения того, что уже знаем.
Учитель: Вспомните, что вы узнали на предыдущих уроках. Что изучает физика?
Ученики: Физика изучает наиболее общие закономерности явлений природы, свойства и строение вещества и свойства физического поля.
Учитель: Каковы основные методы исследования природы?
Ученики: Эксперимент и моделирование.
Учитель: Что представляют собой объекты исследования физики?
Ученики: Объектами исследования в физике являются явления природы, различные тела, вещество, физическое поле.
Учитель: Что такое физическая величина?
Ученики: Количественная характеристика физических явлений, свойств тел, физических полей.
Учитель: Приведите примеры физических величин.
Ученики: Масса тела, время, длина и т. д.
Учитель: Что означает «измерить величину»?
Ученики: Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу.
Учитель: Назовите основные единицы Международной системы единиц (СИ).
Приведите примеры производных единиц СИ (ученики называют).
Учитель: Назовите две важнейшие характеристики измерительного прибора.
Ученики: Цена деления и предел измерения.
Учитель: Чем отличается прямое измерение от косвенного?
Ученики: Измерение физических величин с помощью измерительных приборов — прямые измерения, косвенные измерения осуществляют при расчете физической величины по формуле через величины, значения которых измерены приборами, т. е. сделаны прямыми измерениями.
Учитель: Возьмите набор № 1 трех цилиндров. Что можно сказать о телах при их рассмотрении?
Ученики: Эти тела имеют одинаковую форму, одинаковый объем, на них написано 20 см3, но, кажется, разную массу.
Учитель: Пользуясь рычажными весами и разновесами, определите, какой из цилиндров обладает наименьшей массой, наибольшей массой. Пронумеруйте цилиндры с помощью стикера в порядке убывания их массы. (Учащиеся выполняют задание в парах).
Учитель: Я вижу, что задание выполнено.
Что вы установили?
Ученики: Все три цилиндра имеют разную массу.
Учитель: Как вы думаете, почему?
Ученики: Потому что они изготовлены из разных веществ. Самый легкий цилиндр изготовлен из дерева, самый тяжелый — из одного металла, масса другого металлического цилиндра занимает промежуточное значение между массой деревянного и первого металлического цилиндра.
Учитель: Какой вывод из этого исследование мы можем сделать?
Ученики: Значит один и тот же объем разных веществ имеет разную массу.
Учитель: Действительно, это исследование показывает, что массы одинакового объема разных веществ различны. Все дело в веществе, из которого изготовлено тело. Оказывается, любое вещество характеризуется плотностью, которая показывает, чему равна масса единицы объема вещества. Как вы думаете, чему равна плотность веществ, из которых изготовлены цилиндры? Что это за вещества? Можете ли вы ответить на эти вопросы?
Ученики: Мы не знаем точно, что такое плотность и как ее найти.
Не знаем, как определить вещество. Мы затрудняемся ответить на эти вопросы.
- Объяснение нового материала (процесс получения новых знаний).
Учитель: Запишите тему нашего урока: «Плотность вещества. Косвенное измерение плотности вещества» (Ученики записывают тему в тетрадях, учитель на доске).
Учитель: Ребята, сформулируйте, пожалуйста, цели урока.
Ученики (с учетом корректировки учителя цели фиксируются на доске в виде табличек, прикрепленных магнитами к доске):
Учитель: Какими инструментами вы будете пользоваться для достижения этих целей?
Ученики: Нам, наверняка поможете вы, а также будем пользоваться учебником.
Учитель (объяснение учителя, запись основного материала на доске, запись опорного конспекта учениками в своих тетрадях): Как ранее было сказано,
(учитель прикрепляет табличку на доске).
В ваших исследованиях объемы цилиндров составляли 20 см3,единицей объема можно считать 1 м3 или 1 см3.
Что удобнее найти в вашем случае?
Ученики: Массу 1 см3 вещества, из которого изготовлены цилиндры.
Учитель: Почему?
Ученики: Мы знаем массу цилиндров объемом 20 см3, можно найти и массу 1 см3 вещества цилиндра.
Учитель: Как же это сделать?
Ученики: Надо массу цилиндра разделить на его объем, в нашем случае на 20 см3
Учитель: Действительно, что бы найти плотность вещества надо массу тела из этого вещества разделить на объем тела (прикрепляет очередную табличку к доске):
Учитель: В физике пользуются формулами, где физические величины вместо слов записывают буквами. Вы уже знаете, как обозначается масса и объем. А как же обозначается плотность? Плотность обозначается греческой буквой ρ (читается «ро»).
Попробуйте записать формулу для расчета плотности. Кто-нибудь готов проговорить ее вслух?
Ученики: Формула такова: ρ=m/V.
Учитель: Действительно, формула для расчета плотности тела:
Учитель: Теперь вернемся к массе наших цилиндров.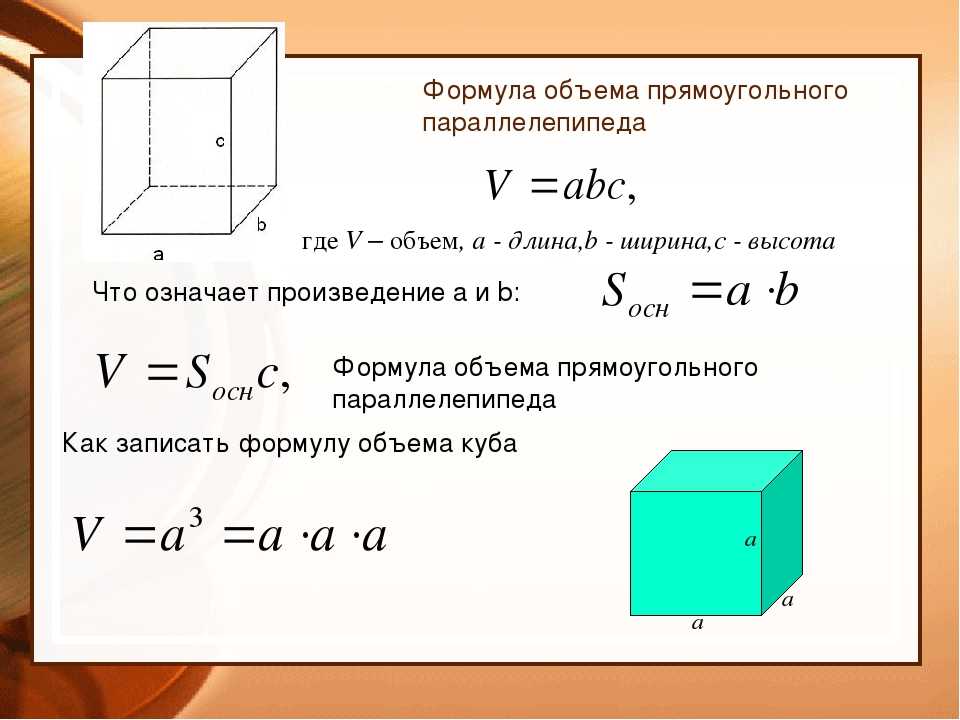
Чему она равна?
Ученики: 156 г, 54 г и 14 г соответственно.
Учитель: Ребята, единицей плотности вещества в СИ является. 1кг/м3. На практике используются другие единицы плотности: 1 г/см3 и 1т/м3. В вашем случае при нахождении плотности у нас получается, что она будет выражена в г/см3. Как же оформить решение трех задач: задач по нахождению плотности цилиндров? Оказывается, это надо делать следующим образом. Слева в тетрадях, а мне на доске, надо записать номер задания, а затем записать слово «Дано:», под ним исходные данные: в вашем случае это результаты прямых измерений массы и объема тела. А потом уже обозначение той величины, которую надо найти. Справа пишется формула, по которой рассчитывается неизвестная величина, на следующей строке непосредственные расчеты. А затем ответ. Получается так.
Можно оформить решение трех задач в одном примере:
Учитель: Вы нашли плотность трех веществ. Как это было сделано: прямым или косвенным измерением?
Ученики: Косвенным измерением, мы рассчитали плотность по формуле, а массу и объем нашли непосредственно измерением.
Учитель: Да, действительно при похожих ситуациях на практике массу измеряют на весах, для измерения объема тела можно также прибегнуть к формулам, если это правильная геометрическая фигура (куб, прямоугольный параллелепипед), или же найти объем с помощью мензурки — измерительного цилиндра.
Учитель: Как же определить, из какого вещества изготовлены цилиндры по найденной плотности?
Ученики: Затрудняемся ответить.
Учитель: Существуют справочные таблицы, где указаны плотности веществ. В нашем учебнике такая таблица находится на стр.21–22. В ней приведены плотности некоторых веществ. Обратите внимание, что там выражена плотность веществ в кг/ м3. Как же связаны между собой разные единицы плотности? Для этого надо вспомнить связь между различными единицами массы: 1 т, 1 кг и 1 г.
Ученики: 1 т = 1000 кг, а 1 кг =1000 г.
Учитель: На самом деле, плотность вещества, выраженная в единицах СИ, т. е. выраженная в кг/м3 будет отличаться в 1000 раз от плотности того же вещества, выраженной в г/см3.
Например, в столбце твердые вещества первым идет золото. Его плотность равна 19 300 кг/ м3. Это означает, что 1 м3 золота будет иметь массу 19300 кг.
С другой стороны, плотность золота равна 19,3 г/ см3. Это означает, что 1 см3 золота будет иметь массу 19,3 г (фиксирует равенство на доске).
Вы рассчитали плотности трех веществ. Определите по таблице, что это за вещества?
Ученики: Первый цилиндр железный, второй — алюминиевый, третий изготовлен из дуба.
Учитель: Что означает, что плотность каждого вещества равна определенному значению?
Ученики: Например, плотность железа равна 7,8 г/см3. Это означает, что 1 см3 железа имеет массу 7,8 г, а соответственно алюминия — 2, 7 г, дуба 0,7 г.
Учитель: Вспомните, какой из цилиндров самый тяжелый?
Ученики: Из железа.
Учитель: Что можно сказать о его плотности по отношению к плотностям других цилиндров?
Ученики: Она самая большая.
Учитель: Какой вывод можно сделать о связи массы тел с их плотностью при одинаковом объеме?
Ученики: Если тела имеют одинаковый объем, то чем больше масса тела, тем больше плотность вещества этого тела, или чем больше плотность вещества тела, тем больше будет масса этого тела.
Учитель: Как же из формулы для определения плотности найти массу тела?
Ученики: Чтобы найти массу тела, нужно плотность вещества тела умножить на объем этого тела, т. е. m= ρ*V.
Учитель: Действительно (закрепляет формулу на доске):
Учитель: А как их формулы для нахождения плотности найти объем?
Ученики: Чтобы найти объем тела, нужно массу тела разделить на плотность вещества этого тела, т. е. V = m/ ρ.
Учитель: Да, на самом деле
Учитель: Что можно сказать о телах одинаковой массы изготовленных из разных веществ?
Ученики: Из этой формулы видно, что если масса тел одинакова, то тело с большей плотностью вещества будет иметь меньший объем, а тело с меньшей плотностью вещества будет иметь больший объем.
- Первичное закрепление нового материала.
Учитель: Итак, вы познакомились с формулой для нахождения плотности вещества. Вы также узнали, как найти массу вещества и объем вещества по его плотности.
Перед вами задания, которые вам предстоит выполнить:
Задание 1 (выполняется фронтально). Определите объем твердого тела, если шкала мензурки проградуирована в см3.
Задание 2 (выполняется в парах).
Определите плотность вещества, из которого изготовлено тело.
Задание 3 (выполняется самостоятельно). Каков объем медного цилиндра массой 89 г.
Задание 4 (выполняется самостоятельно).
Войдет ли 4 кг меда в банку вместимостью 3 л?
(Подсказка: 3л = 3 дм3 = 0,003 м3)
(В ходе работы на уроке, в том числе и при решении задач можно выставлять хорошие отметки по желанию учащихся).
Учитель (после выполнения заданий 2–4 выводит решение задачи, по которому ученики себя проверяют). Ребята, у кого задания вызвали трудности при выполнении? Почему они у вас возникли? Что надо делать, что ошибок не было? Где могут пригодиться полученные знания? (получает ответы на вопросы).
5. Рефлексия учебной деятельности.
Учитель: Что нового вы узнали на уроке? Достигли ли мы поставленных целей? Какие личные качества вам помогли при достижении цели? (слушает ответы учеников).
Учитель: Оцените свою работу на уроке: поставьте свои руки локтями на парту, а ладонями изобразите чаши весов. В левой чаше-ладони представьте весь объем знаний и умений по сегодняшней теме, а в правой — полученный и усвоенный вами объем знаний и умений по этой теме. Покажите, в каком положении оказались ваши чаши-ладони. Проанализируйте это положение, а выводы мы сделаем вместе (анализ ситуации) и поставим новые цели.
(Учитель задает дифференцированное домашнее задание)
Учитель: Спасибо! До свидания.
Литература:
- Хижнякова Л. С., «Физика, 7 класс», М.:Вентана-Граф, 2014.
- http://koledj.ru/docs/index-6336.html
Основные термины (генерируются автоматически): учитель, ученик, плотность вещества, масса, вещество, масса тела, объем, плотность, тело, формула.
Плотность | Определение, символ, единицы измерения, формула и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы. - Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.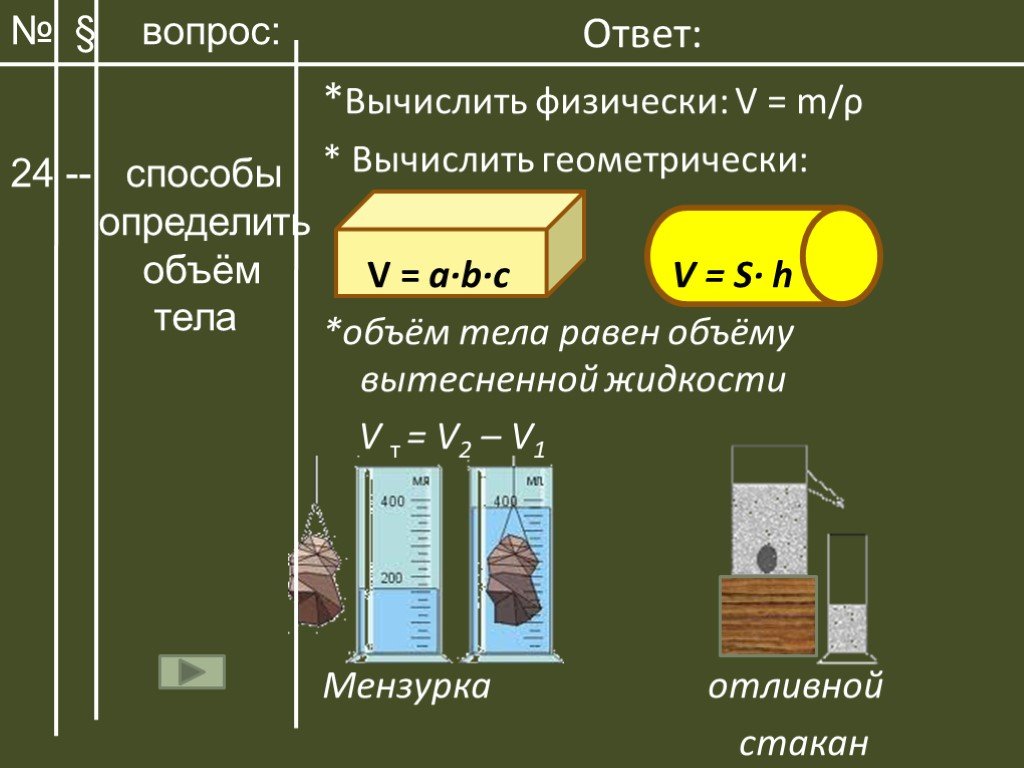 - Britannica Beyond
Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы изучаем широкий спектр тем, которые подпитывают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Связанный контент
Объяснение урока: Расчет плотности | Nagwa
В этом объяснении мы узнаем, как использовать формулу
𝜌=𝑀𝑉 для расчета
плотности различных материалов и предметов.
Плотность — это свойство материалов и объектов, которое измеряет, сколько массы находится в
заданное количество места.
Представьте себе две сферы одинакового размера: одна из железа, а другая из
полистирол. Интуитивно,
мы знаем, что железный шар будет намного тяжелее шара из полистирола.
Железный шар будет иметь большую массу, даже если он того же размера, поэтому мы можем
говорят, что он имеет большую плотность.
Вот почему, например, железный шар утонет в луже воды, а полистироловый
мяч будет плавать.
Несмотря на то, что две сферы имеют одинаковый размер, железный шар имеет большую плотность
чем вода, а значит, он утонет. Однако полистирольная сфера имеет гораздо более низкую
плотность выше, чем у воды, поэтому она будет плавать.
Это будет иметь место независимо от того, насколько велики сферы. Это плотность,
определяет, плавают ли они, а не размер. Итак, если бы у нас была очень большая полистироловая сфера, она все равно
плавать в воде.
Если бы у нас был очень маленький железный шар, он бы все равно утонул.
Плотность объекта обычно обозначается греческой буквой 𝜌 (которая имеет
имя «ро»). Эта буква выглядит как английская буква
𝑝, но если присмотреться, то видно, что он немного другой.
Мы определяем плотность 𝜌 объекта алгебраически как массу,
𝑀, деления объекта на его объем, 𝑉. В виде уравнения это выглядит так
𝜌=𝑀𝑉.
Определение: Плотность
Плотность — это мера массы на единицу объема объекта. Математическая формула для
плотность объекта, который обозначается 𝜌, равна
𝜌=𝑀𝑉,
где 𝑀 — масса объекта и
𝑉 — объем объекта.
Любой объект, сделанный исключительно из одного материала, будет иметь такую же плотность, как и любой другой
объект, сделанный исключительно из
тот же материал. Например, кусок железа объемом
1 м 3 имеет точную
такой же плотности, как
блок железный объемом 100 м 3 .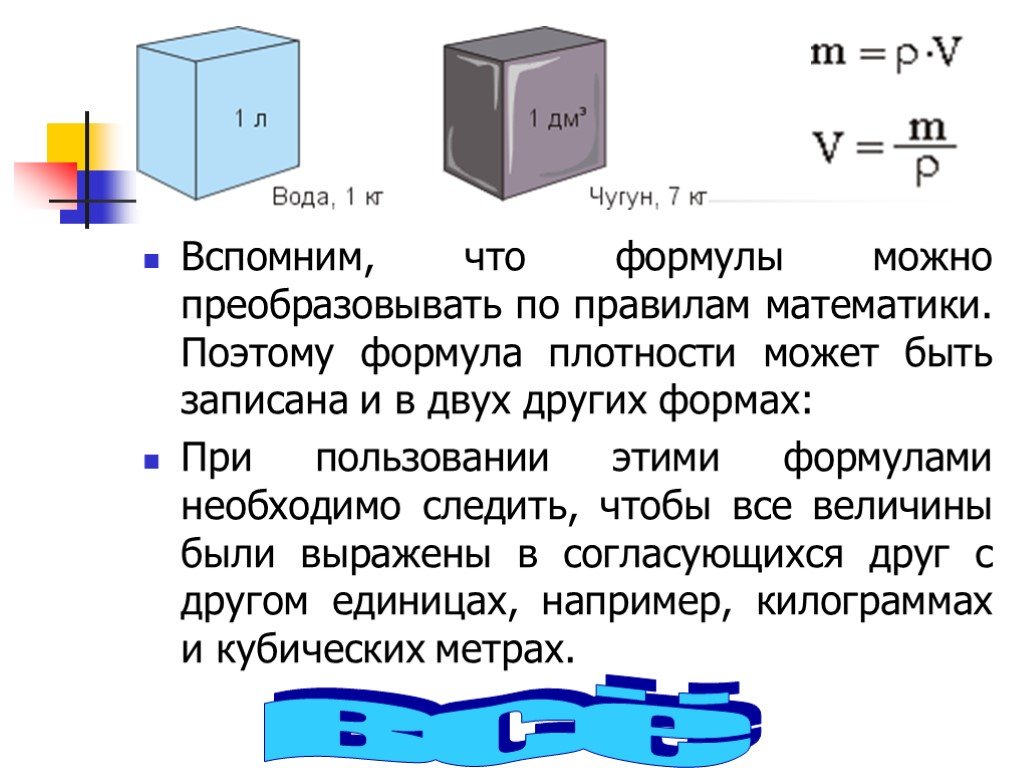
Массы и объемы двух блоков
очень разные, но
плотность блоков одинакова.
Это потому, что плотность блока — это отношение массы блока к
объем блока. Как
объем увеличивается, масса тоже, но соотношение этих двух
количества — плотность — остается неизменной.
Однако некоторые объекты состоят более чем из одного материала. Если каждый из этих
материалы имеют разный
плотность, то плотность всего объекта будет разной в разных частях
объекта.
Например, представьте себе сферу, сделанную частично из полистирола и частично из железа. Поперечное сечение
эта сфера показана на диаграмме ниже. Плотность в части шара из полистирола равна
много меньше, чем плотность части сферы, сделанной из железа.
Если 𝑀 — масса всей сферы и 𝑉
объем всей сферы, то 𝜌=𝑀𝑉 даст
средняя плотность шара. Эта плотность будет иметь значение, равное
между плотностью полистирола и плотностью железа.
Важно помнить об этой разнице.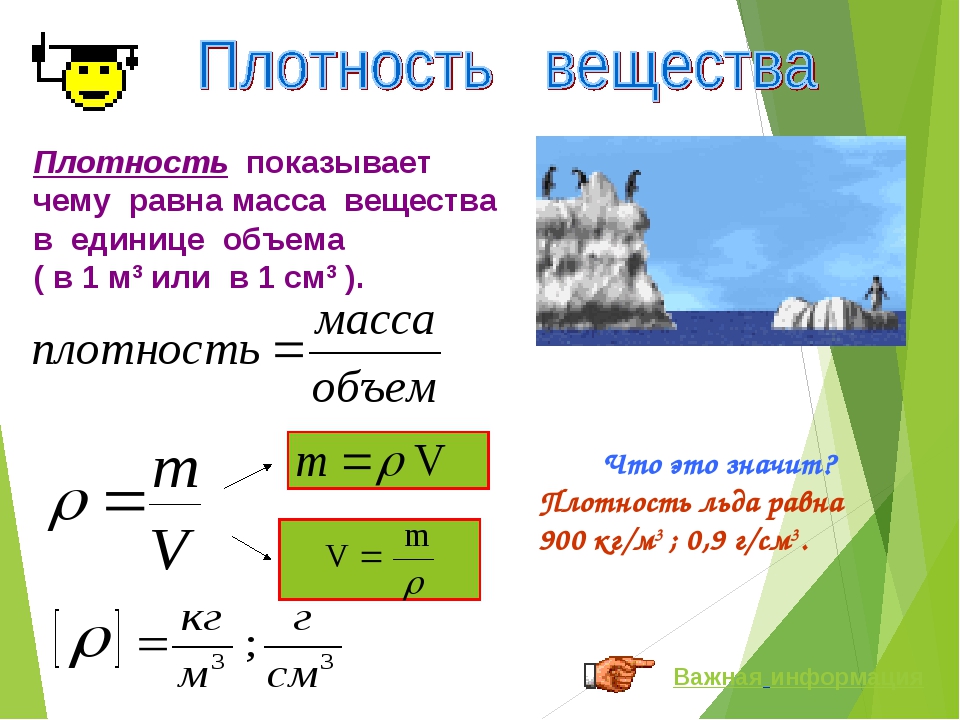
Для конкретного материала плотность
этот материал является собственностью
которую можно найти, и любой объект, сделанный исключительно из этого материала, будет иметь это
плотность.
Однако плотность объекта, состоящего из нескольких материалов, зависит от
этот объект. Мы можем использовать
𝜌=𝑀𝑉, где 𝑀 — масса
весь объект, а 𝑉 — объем всего объекта, чтобы найти
средняя плотность всего объекта.
Пример 1. Определение плотности объекта по его массе и объему
Куб имеет массу
30 кг. Если объем куба
0,02 м 3 ,
какова его плотность?
Ответ
Плотность объекта определяется выражением 𝜌=𝑀𝑉,
где 𝑀 – масса
объект, а 𝑉 — объем объекта.
В этом вопросе нам говорят, что масса куба равна
𝑀=30кг и объем
куб это
𝑉=0,02м.
Нам нужно подставить известные нам значения массы и объема куба
в уравнение
для плотности.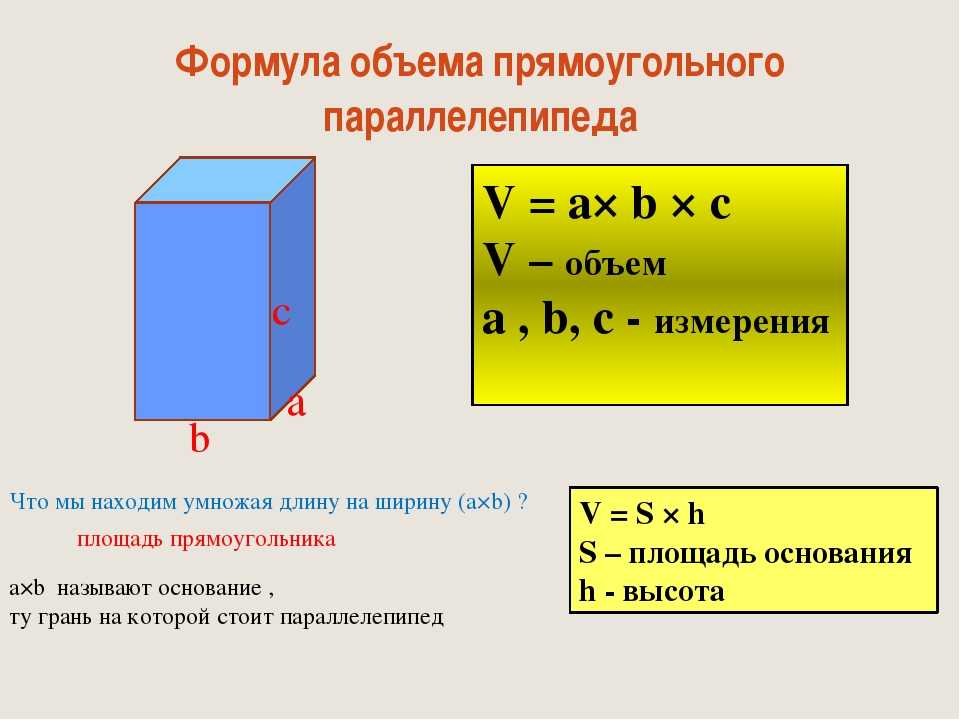
Это дает нам
𝜌=𝑀𝑉=300.02.kgm
Разобьем эту дробь на числовую часть и часть единиц. Мы можем рассчитать числовое значение
часть как 300,02=1500. Единицы в дроби можно просто оставить как
килограмм на кубический метр.
В результате наш окончательный ответ:
𝜌=1500.kgm
Если нам нужно вычислить плотность куба, мы можем это сделать, если знаем массу
куба и длину одной из его сторон.
Напомним, что объем куба со стороной 𝑙 определяется выражением
𝑉=𝑙.
Давайте рассмотрим несколько примеров использования формулы плотности.
Пример 2. Определение плотности объекта по его массе и размерам
Небольшой железный куб имеет длину стороны
0,15 м. Если масса куба
26,6 кг, что это такое
плотность? Дайте ответ ближайшему
килограмм на кубический метр.
Ответ
В этом вопросе нам дана масса,
𝑀=26,6 кг, железного куба, а также
его боковая длина,
𝑙=0,15м.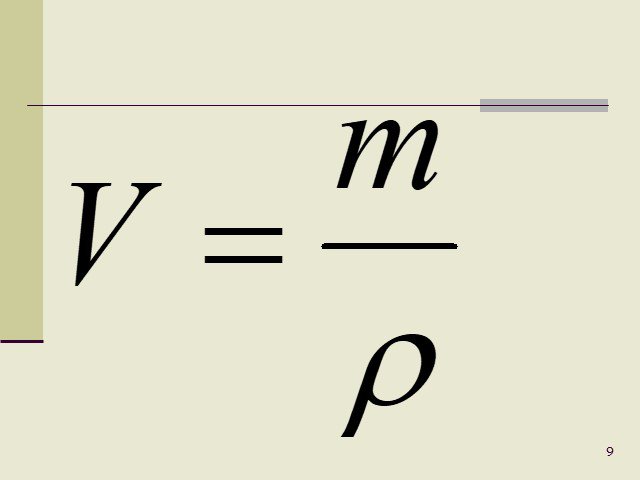
Учитывая это, нас просят найти плотность 𝜌 куба. Напомним, что
формула плотности
𝜌=𝑀𝑉.
Мы знаем массу куба, но не знаем объем куба. Мы можем отработать
объема по формуле объема куба, которая
𝑉=𝑙. Итак, здесь у нас есть
𝑉=(15)=0,15=0,003375.ммм
Теперь мы можем определить плотность железного куба. Нам нужно заменить
масса 𝑀=26,6 кг и объем
𝑉=0,003375m в наше уравнение плотности. Это дает
𝜌=𝑀𝑉=26.60.003375.kgm
Теперь мы можем упростить этот результат, вычислив сначала числовое значение
26,60,003375=7881,48148. Мы можем оставить единицы как есть, т.е.
килограмм на кубический метр. Это означает
𝜌=7881,48148.kgm
Вопрос просит нас дать наш ответ ближайшему
килограмм на кубический метр, что означает, что наш окончательный ответ
𝜌=7881.kgm
Пример 3. Нахождение объема объекта по его массе и плотности
Найдите объем алюминиевого блока массой 54 кг.
Используйте значение 2 700 кг/м 3
для плотности алюминия.
Ответ
В этом вопросе нам дают плотность блока алюминия и просят
найти объем
блокировать. Нам говорят, что блок имеет массу, которую мы назовем 𝑀, равной
54 кг. Нам также сообщают, что
плотность алюминия, из которого сделан блок, составляет
𝜌=2700/кгм.
Мы можем изменить нашу формулу для плотности, 𝜌=𝑀𝑉,
и использовать его для расчета объема этого блока. Если мы
умножаем обе части уравнения плотности на объем 𝑉, получаем
𝑉𝜌=𝑀.
Затем мы можем разделить обе части уравнения на плотность 𝜌, что дает нам
𝑉=𝑀𝜌.
Теперь нам нужно подставить известные нам значения для 𝑀 и
𝜌 в это уравнение. Это дает нам
𝑉=542700.kgkgm
Разобьем эту дробь на числовую часть и единицы. Мы можем вычислить числовую часть
быть 542700=0,02.
Для единиц измерения мы можем сначала разделить верх и низ дроби на
килограммов, и мы видим, что все
кг вычесть из дроби. Во-вторых,
если мы умножим верх и низ дроби на
кубометры,
мы видим, что m 3 отменяется на дне,
но у нас есть коэффициент m 3 сверху. Это означает, что
в общем у нас
𝑉=0.02.m
Таким образом, наш окончательный ответ состоит в том, что объем алюминиевого блока равен
0,02 м 3 .
Пример 4. Определение массы объекта по его объему и плотности
Выяснено, что корона из цельного золота имеет объем
150 см 3 . Найдите массу золотой короны,
используя значение
19 300 кг/м 3 для плотности золота. Дайте ответ с точностью до одного десятичного знака.
Ответ
В этом вопросе нам дан объем 𝑉 и плотность
𝜌 золотой короны и являются
попросили найти массу 𝑀 короны.
Давайте начнем с нашего уравнения для плотности,
𝜌=𝑀𝑉, и умножьте обе части на объем, 𝑉, чтобы получить
𝑀=𝜌𝑉.
Это говорит нам о том, что масса кроны — это просто плотность кроны, умноженная на объем
короны.
Однако, прежде чем мы вычислим массу, мы должны заметить, что плотность
корона дана нам
в килограммах на кубический метр,
тогда как объем короны дан нам в
кубических сантиметров.
Это означает, что прежде чем мы начнем объединять эти две величины, нам нужно
преобразовать их в
сопоставимые единицы. Здесь это означает, что мы должны преобразовать объем в
кубических метров.
Напомним, что 100=1см. Это значит, что
(100)=1см, и, таким образом,
1000000=1см.
Это означает, что нам нужно разделить объем на
кубических сантиметров на
1 000 000. Громкость
короны, в кубических метрах, тогда
𝑉=0,00015.м
Теперь мы можем заменить известные нам значения 𝜌 и
𝑉 найти массу
корона быть
𝑀=19300×0,00015=(19300×0,00015)×=2,895.
kgmmkgmmkg
Вопрос требует, чтобы наш ответ давался с точностью до одного десятичного знака, поэтому
наш окончательный ответ для массы
корона 2,9 кг.
Обратите внимание, что в этом вопросе нам не нужно было знать точную форму
корона. Пока мы
сообщив его объем, мы можем использовать уравнение для плотности, чтобы найти его массу.
Мы можем рассчитать плотность сферического объекта, если знаем массу шара,
𝑀 и радиус сферы 𝑟. Зная эти величины, мы можем использовать
уравнение для плотности, которое
𝜌=𝑀𝑉,
вместе с уравнением объема шара, которое
𝑉=43𝜋𝑟.
Если мы объединим эти два уравнения, подставив выражение для объема
сферу в
уравнение для плотности, то мы видим, что плотность сферы определяется выражением
𝜌=𝑀𝜋𝑟.
Если мы умножим верх и низ дроби на 3, то получим
𝜌=3𝑀4𝜋𝑟,
потому что множители 3 сокращаются в нижней части дроби.
Пример 5. Определение плотности сферы по ее массе и радиусу
Шар для боулинга имеет массу 5,5 кг.
Шар для боулинга представляет собой шар радиусом
7 см. Что
плотность шара для боулинга? Дайте ответ ближайшему
килограмм на кубический метр.
Ответ
В этом вопросе нам предлагается вычислить плотность 𝜌 сферического
объект с учетом его массы и радиуса.
Здесь масса шара для боулинга равна
𝑀=5,5 кг и радиус
шар для боулинга 𝑟=7см. Примечание
что вопрос просит нас дать плотность в килограммах на кубический метр, так что это будет полезно для нас
перевести радиус, данный нам в сантиметрах, в
метров, прежде чем мы начнем.
Это делается путем деления радиуса в сантиметрах на 100,
поэтому 𝑟=0,07 м.
Поскольку теперь мы знаем всю необходимую информацию, мы можем использовать уравнение для плотности сферы,
который
𝜌=3𝑀4𝜋𝑟.
Нам просто нужно подставить значения для 𝑀 и 𝑟 для этого вопроса. Если мы сделаем это,
мы нашли
𝜌=3×(5,5)4𝜋×(0,07).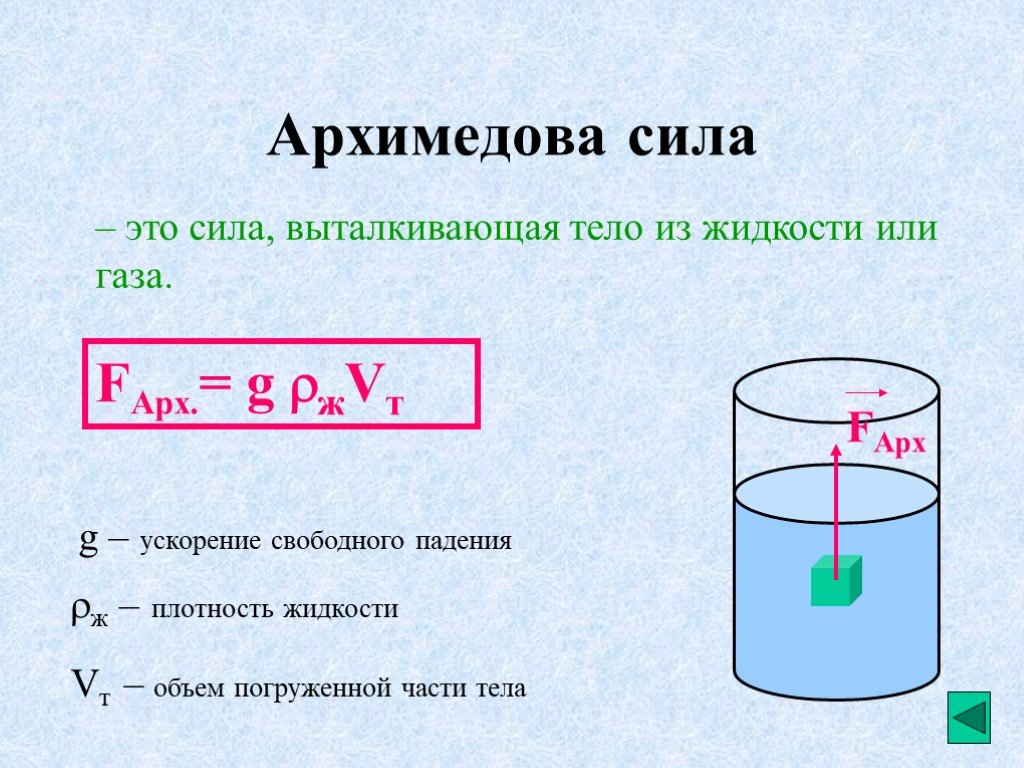
kgm
Если мы решим это, не забывая возводить в куб как число, так и единицы измерения
знаменатель, находим
𝜌=3828.07….kgm
Нас просят передать наш ответ ближайшему
килограмм на кубический метр,
так что наш окончательный ответ просто
𝜌=3828.кгм
Пример 6. Определение объема объекта по его массе и плотности
Стальной шарикоподшипник имеет массу 0,034 г. Найдите диаметр шарикоподшипника в
миллиметры,
округляется до ближайшего миллиметра. Используйте значение
8 000 кг/м 3
для плотности стали.
Ответ
В этом примере нам дана масса
𝑀=0,034 г сферического шара
подшипник, а также его плотность,
𝜌=8000/кгм. Учитывая это, нас просят найти диаметр шарикоподшипника.
Назовем диаметр шарикоподшипника 𝑑 и вспомним, что диаметр в два раза больше радиуса. Итак, если радиус шарикоподшипника равен 𝑟, то
𝑑=2𝑟.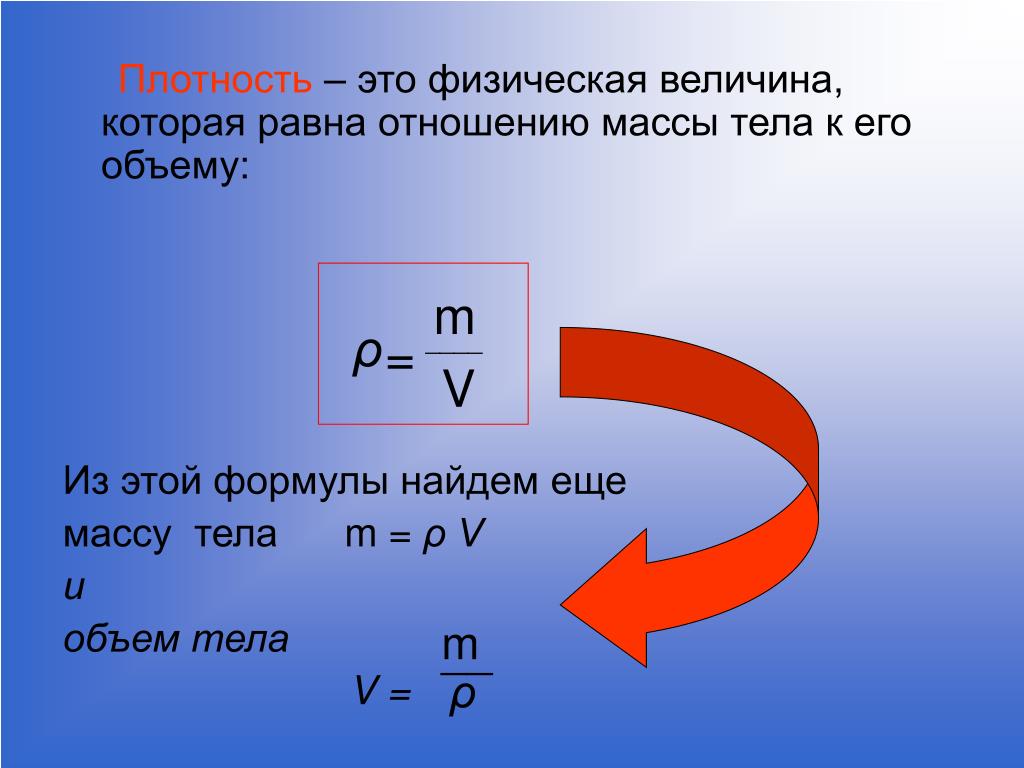
Имея это в виду, давайте сначала вычислим радиус
шарикоподшипника, используя уравнение плотности для сферы.
Давайте начнем с изменения уравнения плотности для сферы, чтобы мы могли его использовать
найти радиус 𝑟. Плотность сферы определяется выражением
𝜌=3𝑀4𝜋𝑟.
Сначала умножим обе части этого уравнения на 𝑟. Это дает нам
𝜌𝑟=3𝑀4𝜋.
Мы можем разделить обе части на 𝜌, чтобы получить
𝑟=3𝑀4𝜋𝜌.
Теперь правая часть этого уравнения включает только члены, которые мы знаем
значение.
Единственным дополнительным шагом здесь является преобразование массы шарикоподшипника, который
дается нам в граммах, в
килограммы. Мы хотим сделать это, потому что плотность стали дана нам в единицах
килограмм на кубический метр.
Мы делаем это, уменьшая массу в граммах на 1 000, поэтому масса шарикоподшипника равна
𝑀=0,000034.кг
С этим номером будет намного проще работать, если мы напишем его научным языком.
обозначение. Это дает нам
𝑀=3,4×10кг.
Мы можем заменить значения 𝑀 и
𝜌 что мы должны сейчас получить
𝑟=3×3,4×104𝜋(8000/).кгкгм
Обратите внимание, что единицы
кг отменить, и вообще,
единицы становятся m 3 . Мы также можем вычислить числовую часть этой дроби как
3×3,4×104×8000=1,0146×10,
Это означает, что мы нашли значение радиуса в кубе равным
𝑟=1,0146×10,m
Теперь нам нужно извлечь кубический корень из этого выражения, чтобы найти радиус
шариковый подшипник, который дает
𝑟=0,001004847…,м
где мы взяли кубический корень единиц, а также числа. Вопрос
просит нас дать
наш ответ в миллиметрах,
поэтому давайте преобразуем наш ответ (в метрах)
в миллиметры. Это делается путем умножения
на 1 000, и так
𝑟=1,004847….мм
Нам нужно удвоить радиус 𝑟, чтобы найти диаметр 𝑑 шарикоподшипника,
как задается вопрос.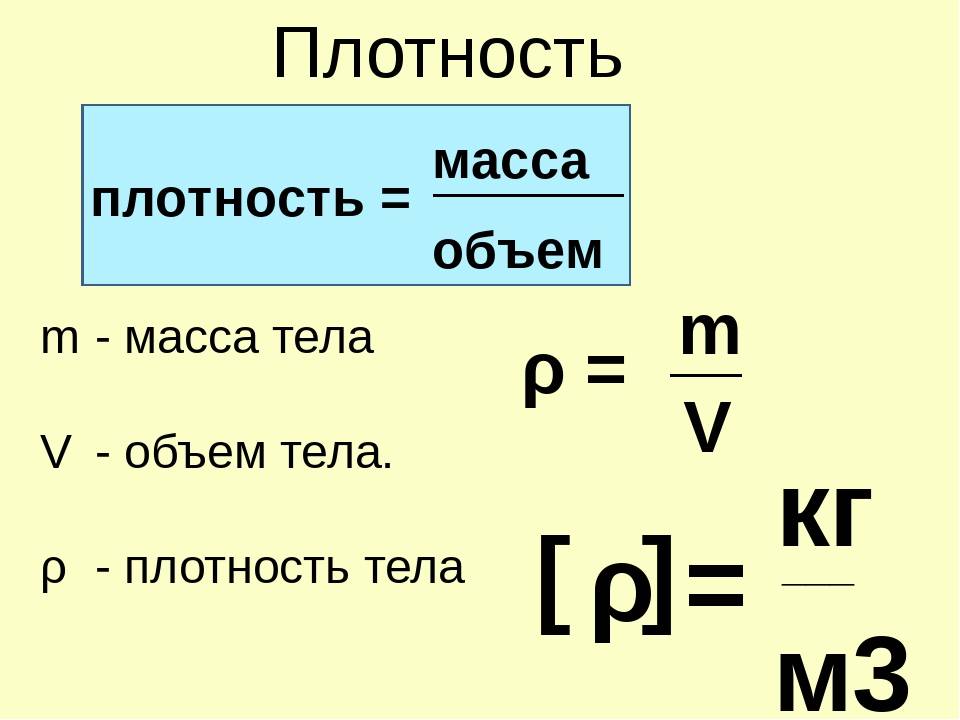
Это, до ближайшего
миллиметр, дает
𝑑=2𝑟=2,мм
Это наш окончательный ответ: диаметр шарикоподшипника
2 мм.
Мы также можем захотеть вычислить плотность объекта с менее правильными размерами,
например, прямоугольная призма длиной 𝑙, шириной
𝑤 и высота ℎ.
В этом случае объем 𝑉 прямоугольной призмы равен
𝑉=𝑙𝑤ℎ.
Это означает, что, объединив эту формулу объема с нашим уравнением для плотности
объекта, мы можем
говорят, что плотность прямоугольной призмы материала равна
𝜌=𝑀𝑉=𝑀𝑙𝑤ℎ.
Пример 7. Определение плотности объекта по его массе и размерам
Кирпич имеет массу 3,5 кг. Представляет собой прямоугольную призму со сторонами
23 см,
11 см и
7 см. Какова плотность кирпича? Дайте ответ ближайшему
килограмм на кубический метр.
Ответ
В этом вопросе нам даны размеры и масса прямоугольной призмы и
просят найти его плотность.
Неважно, какое из измерений мы называем длиной, высотой или шириной. Для этого примера давайте
говорят, что длина — это самое длинное измерение, поэтому
𝑙=23см. Скажем так
ширина — средняя длина,
значит 𝑤=11см. Окончательно,
скажем, что высота является наименьшей длиной, поэтому
ℎ=7см.
Обратите внимание, что все эти расстояния указаны в
сантиметров, но мы
просят рассчитать плотность в килограммах на кубический метр. Проще будет перевести расстояния в метры
прежде чем мы приступим к расчету
плотность. Это делается путем деления каждого расстояния на
сантиметров на 100,
и так, размеры кирпича можно записать как
𝑙=0,23,𝑤=0,11,ℎ=0,07.ммм
Это означает, что мы готовы рассчитать плотность кирпича. Мы используем эти размеры вместе с
масса кирпича, о которой нам говорят в вопросе, равна
3,5 кг. Это позволяет нам вычислить
𝜌=𝑀𝑙𝑤ℎ=3,5(0,23)(0,11)(0,07).
кгммм
Мы можем сначала упростить единицы, которые становятся
килограмм на кубический метр, а затем рассчитать числовое значение, которое будет
3,5(0,23)×(0,11)×(0,07)=1976,28….
Это означает, что с точностью до килограмма на кубический метр плотность кирпича равна
𝜌=1976,кгм
и это наш окончательный ответ.
Ключевые моменты
- Плотность — это свойство материалов, которое измеряет массу на единицу объема
материал, который может быть записан как
𝜌=𝑀𝑉,
где 𝜌 — плотность массы, 𝑀 — масса материала,
𝑉 — объем материала. - Для данного материала его плотность всегда одинакова
независимо от формы предмета, изготовленного из этого материала. - Мы можем объединить уравнение для плотности с уравнением для объема для
определенные формы предметов. В частности, для куба с длиной стороны
𝑙, его объем 𝑉=𝑙. - Для прямоугольной призмы длиной 𝑙,
ширина 𝑤 и высота ℎ, его объем
𝑉=𝑙𝑤ℎ.
