Аннотация
«Название программного продукта» «Объём. Объём прямоугольного параллелепипеда».
Номинация: точные науки
Предметная область: математика
Параллель: 5 класс
Вид программного продукта: презентация, составленная в программе Microsoft Power Point, 2007. Режим показа последовательный, управляемый пользователем.
Разработчик: учительница математики МОБУ СОШ д.Кужанак МР Зианчуринский район Республики Башкортостан Гафарова Рузиля Талгатовна.
Конспект урока с использованием информационно – коммуникативных технологий (ИКТ)
Предмет – математика. Урок изучения новой темы.
Тема урока: Объём. Объём прямоугольного параллелепипеда.
Продолжительность урока: 45 минут
Класс: 5 класс
Технологии: Компьютерная технология (как источник учебной информации, как наглядное пособие, как тренажер и как средство диагностики и контроля)
Аннотация: Данный урок проводится в 5 классе по учебнику Н.Я.Виленкина в конце 2 четверти, после изучения темы: «Прямоугольный параллелепипед», где изучались элементы прямоугольного параллелепипеда и площадь поверхности. ( По учебнику А.Г.Мордковича тема изучается в четвёртой четверти.) По программе на изучение темы «Объём. Объём прямоугольного параллелепипеда» отводится 3 часа. Это первый урок – изучение нового материала. Он начинается с проблемной темы, методом беседы, обучающиеся должны сами сформулировать тему урока, цели урока. Путем логического мышления, творческих способностей обучающихся, способностей самостоятельной работы, внимательности, сообразительности, математического моделирования, умений обобщать, делать выводы, сравнивать под руководством учителя, обучающиеся должны изучать и закреплять новую тему. На следующих уроках можно решать задачи практического содержания и рассматривать связи между единицами измерения объёмов. При работе применялись технологии: развивающего обучения, развития мыслительной деятельности и исследовательских навыков, личностно-ориентированного подхода в обучении. Данный урок можно проводить и в начальных классах на занятиях по интересам и в кружках.
Тема урока: Объём. Объём прямоугольного параллелепипеда.
Цели урока: 1)Ознакомление учащихся с понятием объёма, с единицами измерения объёма. Выведение формул для вычисления объёма прямоугольного параллелепипеда и куба. 2) Развитие логического мышления, творческих способностей обучающихся, способностей самостоятельной работы, внимательности, сообразительности, математического моделирования, умений обобщать, делать выводы, сравнивать, способностей применять полученные знания на практике. 3)Воспитание чувства коллективизма, привитие интереса к предмету и окружающему миру.
Оборудование: Таблицы: « Объём», «Формулы». Модели кубов 1 см3, 1дм3, модели фигур, составленные и склеенные из кубиков, раздаточный материал; модели прямоугольного параллелепипеда, других плоских и объёмных тел; компьютер, проекционный экран.
Ход урока
-Учитель: «Ребята, перед началом урока ответьте, пожалуйста, на такой вопрос – что тяжелее: 1кг железа или 1кг ваты?» – «Железо», – говорят обычно дети. ( После выясняется, что массы равны.) – Учитель: «Что же все- таки у них различно?» – Вата много места занимает… (прослушаю ответы до слова объём)
Запишем число, тему урока «Объём».
Совместно с обучающимися сформулируем цели урока. Сегодня мы ознакомимся с понятием объёма, единицами измерения объёма, формулой для вычисления объёма прямоугольного параллелепипеда. ( Слайд 1) Ваша работа будет успешной, если вы: ( Слайд 2) ● покажете знания изученных величин и единиц их измерения; ● будете активно участвовать в исследовании, выражать собственное мнение и давать высказываться другим; ●ваша деятельность на уроке покажет, что вы понимаете, что такое объем и можете его вычислить; ● сможете вывести формулу объема куба и прямоугольного параллелепипеда.
– Вы, слышали слово «объём»? Можете ли придумать синоним этому слову? Составьте предложения с этим словом. ( Вместимость) – В жизни нам приходится измерять вместимость сосудов, различных тел, т. е. измерять объём. Ребята приводят примеры: люди вычисляют объёмы деталей, комнат, стройматериалов, собранного урожая, стогов сена и т.д. – А все ли тела, все ли фигуры имеют объёмы? ( Слайд 3) На какие 2 группы можно разбить эти геометрические фигуры? (Какие из этих фигур имеют объёмы, какие нет?) (Слайд 4) -Какие виды фигур перед вами? (плоские, объёмные) – Как называется каждая фигура? – Чем они отличаются? (плоские: длина, ширина; объёмные: длина, ширина, высота.) – Сегодня наша задача, какая? – Научиться вычислять объёмы тел. – Работа, которую вы сейчас выполните, развивает очень важные для вас исследовательские навыки; такие как классификация данных и умение работать в паре. – Начертите таблицу «Величина», заполните её, обозначив единицы измерения данных величин. (Слайд 5)
ВЕЛИЧИНА
|
ДЛИНА |
МАССА |
ОБЪЕМ |
ПЛОЩАДЬ |
дм, м, га, стакан, ведро, км, г, кг, центнер, т, см², аршин, дм², м², км², мм, см, литр, столовая ложка, га. (Слайд 6) с правильными ответами. Взаимопроверка. Затруднения были? Где? Совершим мысленную экскурсию на кухню, мама делает салат на зиму. Она использует такие единицы объёмы: – Какие? ( Угадай мои мысли – стакан масла, чайную ложку соли, столовую ложку сахара)
– Сегодня на уроке мы узнаем, какие ещё существуют единицы измерения объёма. – Для того чтобы говорить об объёме фигуры, нужно ещё раз вспомнить известную нам единицу измерения объёма – литр. – Для чего литр используется? (для измерения объёма жидкости и вместимости сосудов). – Существуют и другие единицы измерения объёма. В математике принято за единицы измерения объёма – 1см³, 1дм³, 1м³, 1 мм3 ,1 км3 . (показать). Кубик с ребром 1см называется 1см³, с ребром 1 дм – 1дм³, с ребром 1м – 1м³ (показать грань). (Слайд 7)
Сравнить 1см3 и 1дм³. – Что значит измерить объём? – Значит нужно узнать, сколько внутри фигуры вмещается маленьких единичных кубиков. (Слайд 8) – Чему равны объёмы фигур? Есть ли фигуры, имеющие равные объемы? Равны ли сами эти фигуры?
Работа с раздаточным материалом. Из кубиков составлены разные фигуры, нужно определить, чему равен объём, и наоборот составить фигуры, например, объём которых равен 6 см³.
-Как вы думаете, почему взяли именно кубик в качестве мерки? (ребра куба равны между собой) – Любой ли кубик в математике служит единицей измерения объёма? – Нет. Только кубик с ребром 1см, который называется 1см³, с ребром 1 дм – 1дм³, … 1м³, 1 мм3, 1 км3 .
Пока ребята работают с раздаточным материалом строю из единичных кубиков прямоугольный параллелепипед. – Ребята, как быстро сосчитать, чему равен объём этой фигуры, т. е. сколько уместилось единичных кубиков? (Слайд 9) – Узнать сверху, сколько кубиков лежат. Затем умножить на число слоев. – Правильно, молодцы! А что за фигура у нас получилось? – Прямоугольный параллелепипед. Давайте, запишем это правило для вычисления объёма прямоугольного параллелепипеда в виде формулы. И у нас появится ещё одна формула. Объём обозначается большой буквой латинского алфавита – буквой V .
Сейчас каждая пара проводит исследование. Вывод запишите в опорной таблице: (1 кубик считается как 1см³) ● Основание состоит из ___ кубиков. ● S основания (дна) параллелепипеда равна ____см². ● По высоте параллелепипеда выложили ______ таких слоя. ● Объём равен ( □ • □ ) • □ = □ см³ (Слайд 9)
Выведение формулы: – Если три измерения обозначит буквами a, b, c, а объём буквой V, то, как можно записать этот вывод в виде формулы?
V = a • b • c можно пропустить знаки умножения V = a b c или V = S осн. • высота (Слайд 10) ● Сколько видов задач можно составить? – четыре, неизвестно V , неизвестно –a, неизвестно – b, неизвестно – c – А как будет выглядеть формула нахождения объёма куба V= a • a • a или V = a3. ● Сколько видов задач можно составить? – два, неизвестно – V , неизвестно –a . Прочитайте вывод по учебнику.
Физкультминутка.
Закрепление. Решение задач
1.Сформулировать и устно решить задачи по таблице (Слайд 11)
|
№ |
Длина – a |
Ширина – b |
Высота – c |
Объём – V |
|
1. |
5см |
2см |
6 см |
? |
|
2. |
5см |
? |
3 см |
60 см³ |
|
3. |
? |
2 м |
2м |
40 м³ |
|
4. |
15дм |
1дм |
? |
15 дм³ |
2. Пришли срочные телеграммы: 1) от завхоза школы – нужно узнать объём аквариума живого уголка с измерениями a = 4дм, b = 3дм, c = 2дм. ( Слайд 12)
2) от педиатра районной больницы – нужно узнать, сколько м³ воздуха приходится на одного обучающегося в помещении, размеры которого 7х6х3 , если там находится 14 человек. (Слайд 13)
3. Дан куб с объёмом 8 см³. Чему равна сторона куба?
4. Ребята, проявите творческие способности, способности самостоятельной работы, включите сообразительность, составьте свои задачи, разрешается из учебника. (Индивидуальная работа с обучающимися. Желающие 4-5 обучающихся работают у доски, кто-то самостоятельно. Всех проверяю. Самопроверка и взаимопроверка.)
(Слайд 14) (Слайд 15, 16) Для сильных обучающихся, и тех, кто закончил работу
Итоги, выводы.
– Что нового вы сегодня узнали? Имеет ли человек объём? Его сердце?
– Можно ли применять полученные сегодня знания на практике? – 1 дм³ = ? см³. – Как вы думаете, чем будем заниматься на следующем уроке? (Связь между единицами измерения объёма)
(Слайд 17) Самопроверка
Оценки. Из кубиков составьте прямоугольный параллелепипед, объём которого равен оценке, на какую вы усвоили тему урока. Можно нарисовать в тетрадях (Самооценка).
(Слайд 18)
Домашняя работа. 1)Выполнить измерения и вычислить объём твоей спальной комнаты или составить и решить задачу на тему « Объём»
2) узнать, ещё какие единицы измерения объёма существуют (например – баррель что означает). 3) Подумать какие существуют связи между единицами измерения объёма. (Д/з на листочках раздать)
Дополнительно при наличии времени. Можно рассказать легенду об Архимеде « Эврика», или легенду о матери «Сердце матери».
Уже известны единицы измерения длины, например:
— и другие.
Для фигур на плоскости измеряют площадь в соответствующих квадратных единицах измерения:
мм2,см2,дм2,м2,км2…
Для геометрических тел измеряют объём, и для этого необходимы единицы измерения.
Единицей измерения объёма служит объём куба, у которого все грани равны (1) единице измерения длины:

мм3,см3,дм3,м3,км3…
Это кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр или даже кубический километр:
1км3=1000000000м3;1м3=1000дм3=1000000см3;1дм3=1000см3;1см3=1000мм3.
Часто для измерения объёма жидкости используют единицу измерения (1) литр:
1 л =1000см3=1дм3
.
Если измерять объём прямоугольного параллелепипеда, то можно представить, как маленькие кубики перекрывают прямоугольник в основании прямоугольного параллелепипеда.
Длины сторон прямоугольника определяют, сколько кубиков в ряду и сколько рядов с кубиками будет.
|
|
|
Если стороны равны, например, (3) см и (4) см, то прямоугольник перекрывается (3·4 = 12) кубиками.
Высота параллелепипеда определяет, сколько таких слоёв с кубиками можно поставить.
 |
|
Если высота прямоугольного параллелепипеда равна (3) см, то всего получится (3) слоя с кубиками. Итак, всего (3·3·4 = 36) кубиков, или объём равен (36) см³.
Значит, три измерения прямоугольного параллелепипеда позволяют посчитать, сколько всего кубиков поместилось в геометрическом теле, то есть вычислить объём прямоугольного параллелепипеда.
Пусть измерения прямоугольного параллелепипеда будут a, b и c единиц измерения.
Тогда объём (V = a·b·c) кубических единиц измерения.

ОБЪЕМ ФИГУР В ПРОСТРАНСТВЕ
Объем – величина, аналогичная площади и сопоставляющая фигурам в пространстве неотрицательные действительные числа. За единицу объема принимается куб, ребро которого равно единице измерения длины.
Для объемов пространственных фигур справедливы свойства, аналогичные свойствам площадей плоских фигур, а именно:
1. Объем фигуры в пространстве является неотрицательным числом.
2. Равные фигуры имеют равные объемы.
3. Если фигура Ф составлена из двух неперекрывающихся фигур Ф 1 и Ф 2 , то объем фигуры Ф равен сумме объемов фигур Ф 1 и Ф 2 , т.е.
V ( Ф )= V ( Ф 1 )+ V ( Ф 2 ).
Две фигуры, имеющие равные объемы, называются равновеликими.
В режиме слайдов ответы и решения появляются после кликанья мышкой
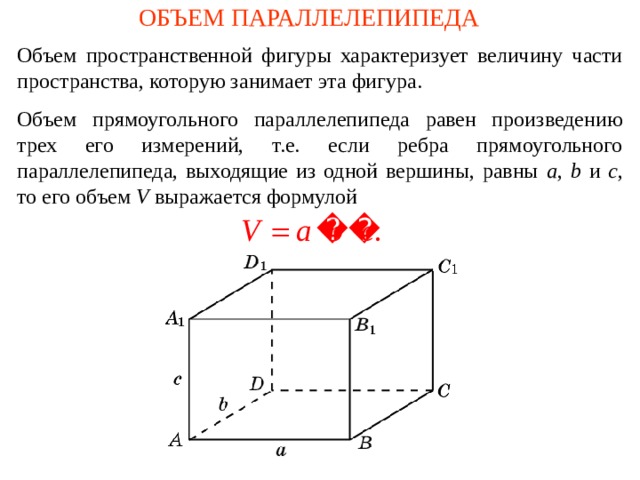
ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА
Объем пространственной фигуры характеризует величину части пространства, которую занимает эта фигура.
О бъем прямоугольного параллелепипеда равен произведению трех его измерений, т.е. если ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны a , b и c , то его объем V выражается формулой
В режиме слайдов формулировки появляются после кликанья мышкой
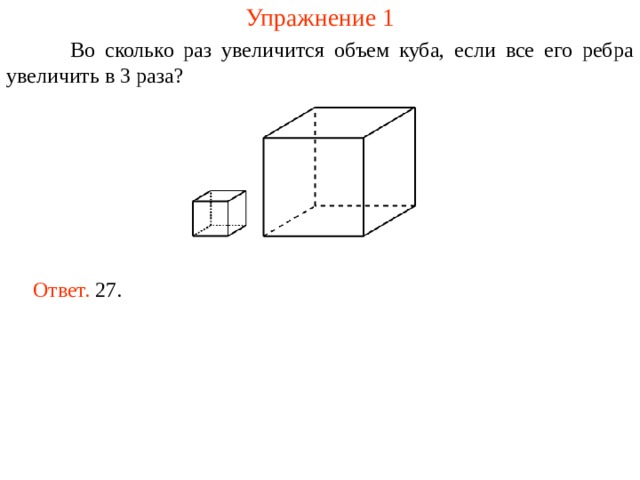
Упражнение 1
Во сколько раз увеличится объем куба, если все его ребра увеличить в 3 раза?
Ответ. 27.
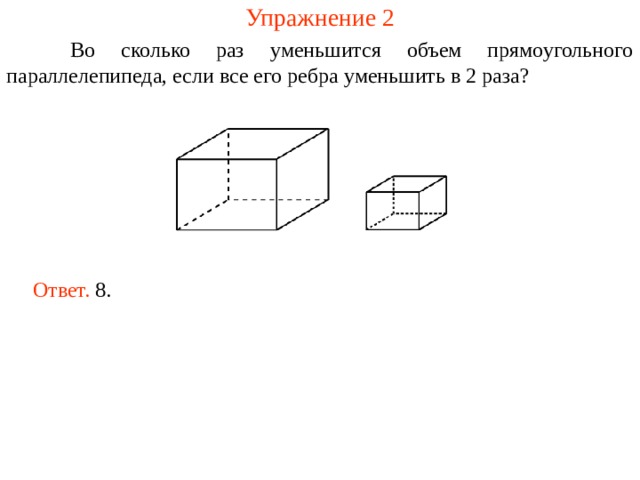
Упражнение 2
Во сколько раз уменьшится объем прямоугольного параллелепипеда, если все его ребра уменьшить в 2 раза?
Ответ. 8.

Упражнение 3
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 3. Каким должно быть третье ребро, выходящее из той же вершины, чтобы объем этого параллелепипеда равнялся 30?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 5.
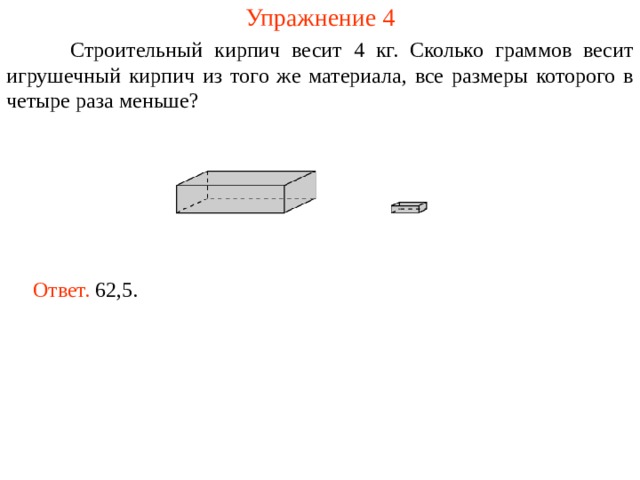
Упражнение 4
Строительный кирпич весит 4 кг. Сколько граммов весит игрушечный кирпич из того же материала, все размеры которого в четыре раза меньше?
Ответ. 62,5.
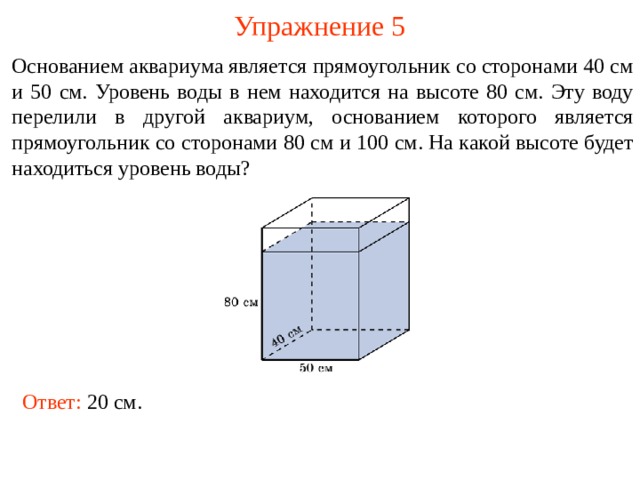
Упражнение 5
Основанием аквариума является прямоугольник со сторонами 40 см и 50 см. Уровень воды в нем находится на высоте 80 см. Эту воду перелили в другой аквариум, основанием которого является прямоугольник со сторонами 80 см и 100 см. На какой высоте будет находиться уровень воды?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 20 см .
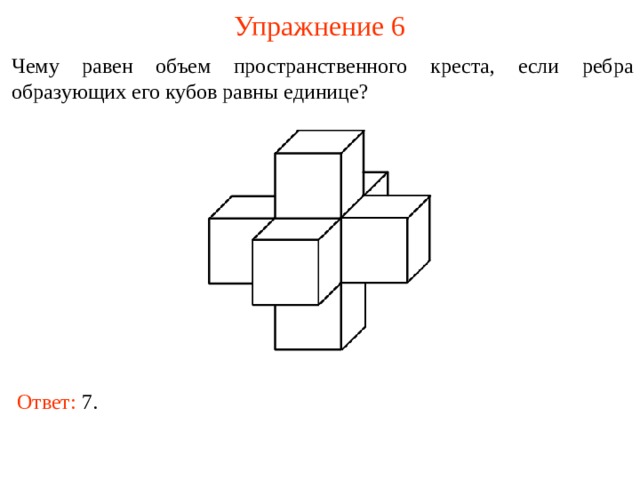
Упражнение 6
Чему равен объем пространственного креста, если ребра образующих его кубов равны единице?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 7 .
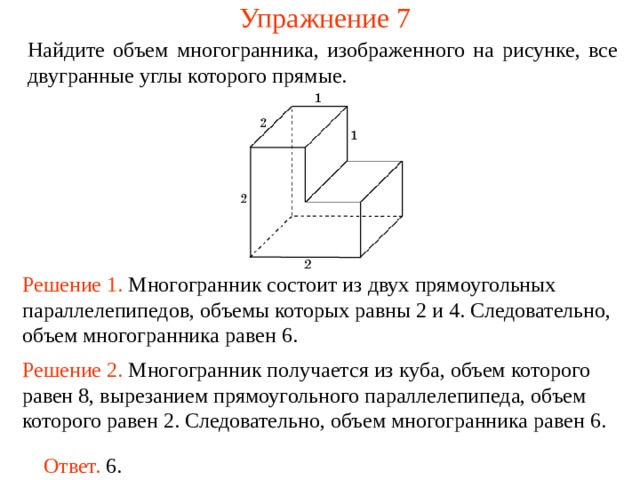
Упражнение 7
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
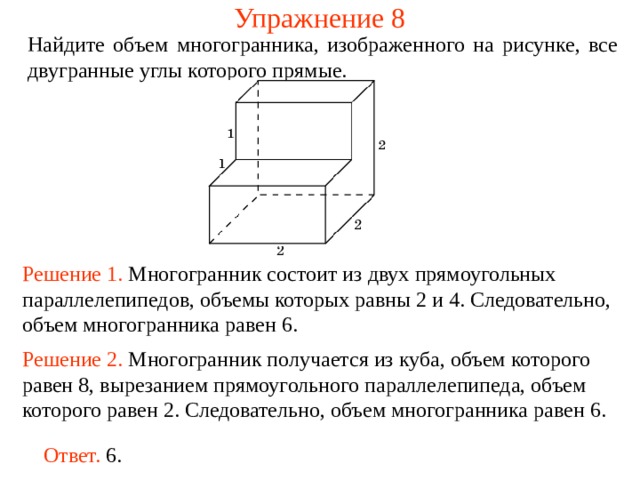
Упражнение 8
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
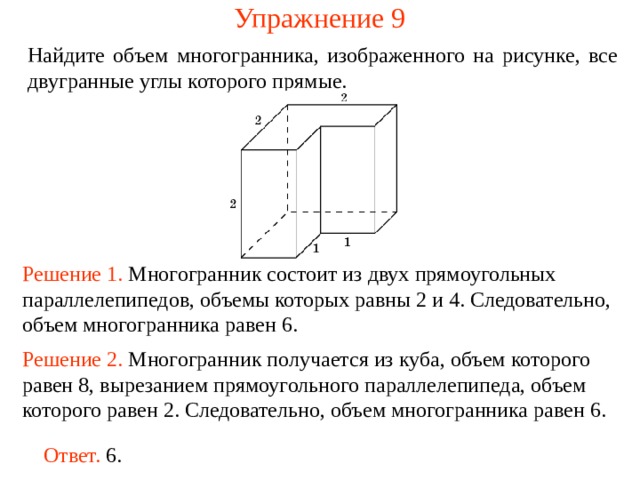
Упражнение 9
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
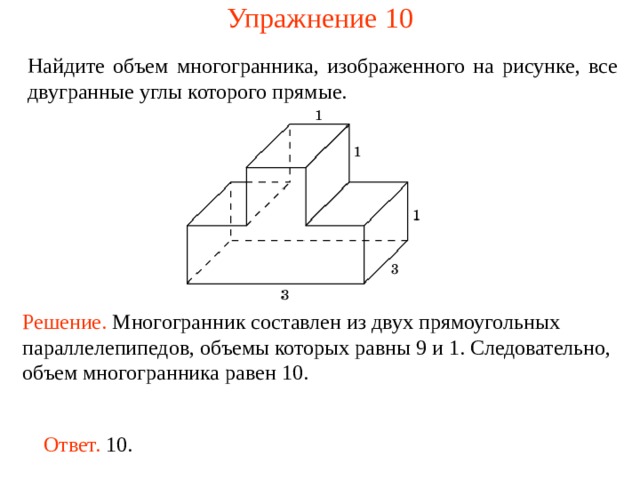
Упражнение 1 0
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник составлен из двух прямоугольных параллелепипедов, объемы которых равны 9 и 1. Следовательно, объем многогранника рав ен 10 .
Ответ. 10.

Упражнение 1 1
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник получается из куба, объем которого равен 8, вырезанием куба, объем которого равен 1. Следовательно, объем многогранника рав ен 7 .
Ответ. 7.

Упражнение 1 2
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник получается из прямоугольного параллелепипеда, объем которого равен 48, вырезанием прямоугольного параллелепипеда, объем которого равен 8. Следовательно, объем многогранника рав ен 40 .
Ответ. 48.
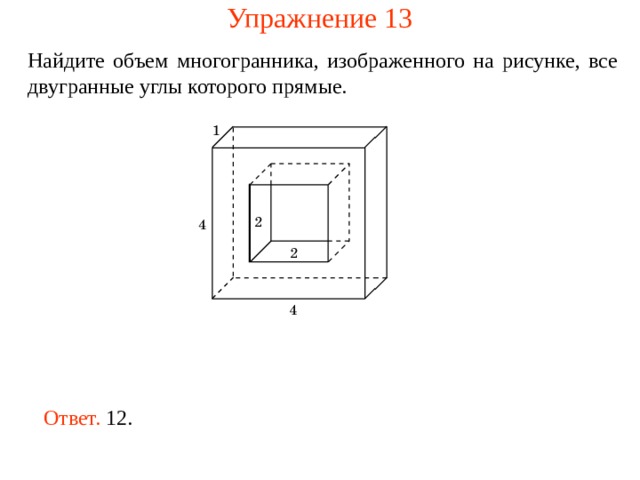
Упражнение 13
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 12.

Упражнение 14
Найдите объем детали, изображенной на рисунке (все углы – прямые).
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1 0 см 3 .
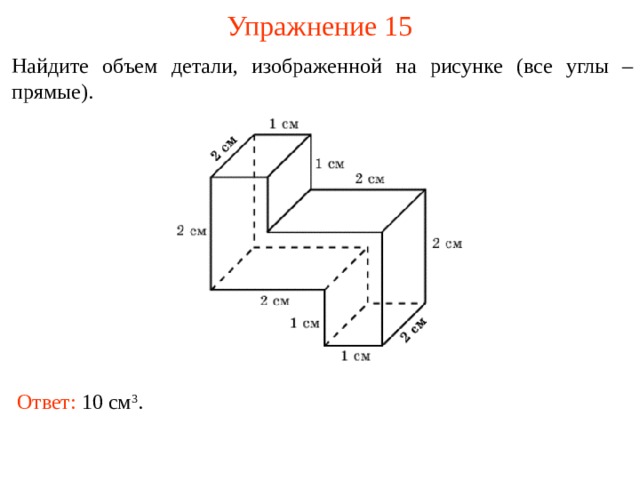
Упражнение 15
Найдите объем детали, изображенной на рисунке (все углы – прямые).
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1 0 см 3 .

Упражнение 16
Найдите объем детали, изображенной на рисунке (все углы – прямые).
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 5 см 3 .
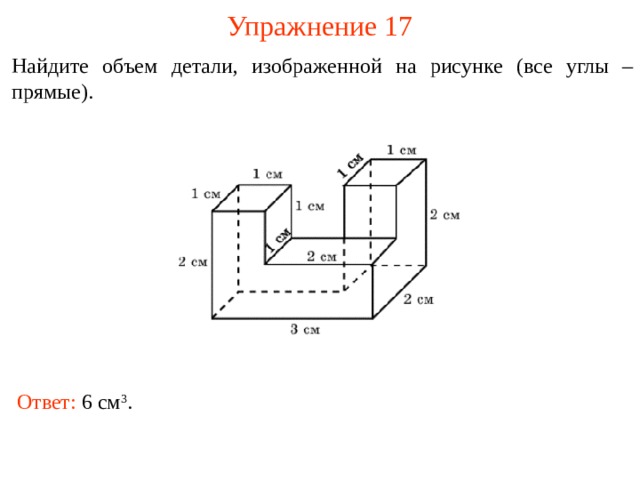
Упражнение 17
Найдите объем детали, изображенной на рисунке (все углы – прямые).
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 6 см 3 .
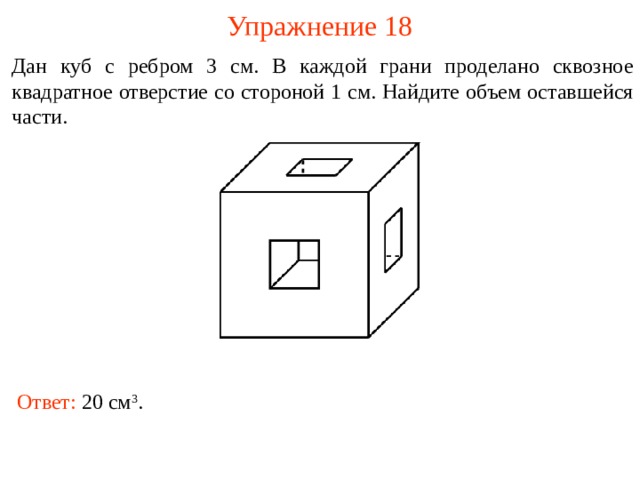
Упражнение 18
Дан куб с ребром 3 см. В каждой грани проделано сквозное квадратное отверстие со стороной 1 см. Найдите объем оставшейся части.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 20 см 3 .
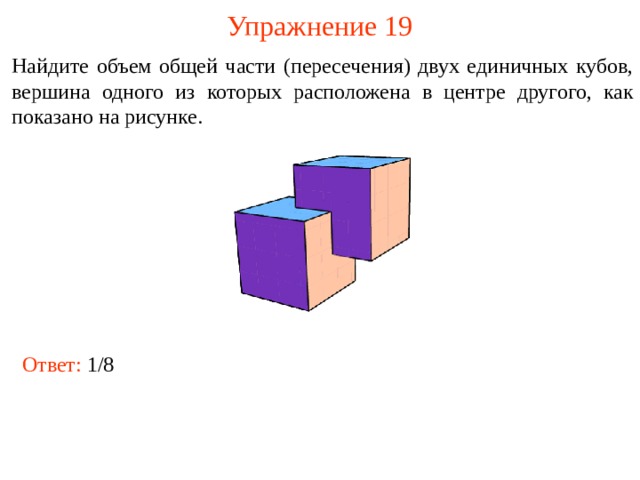
Упражнение 19
Найдите объем общей части (пересечения) двух единичных кубов, вершина одного из которых расположена в центре другого, как показано на рисунке.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1/8

Упражнение 20
Найдите объем фигуры, составленной из двух единичных кубов, две вершины одного из которых расположены в центрах граней другого.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1,75.
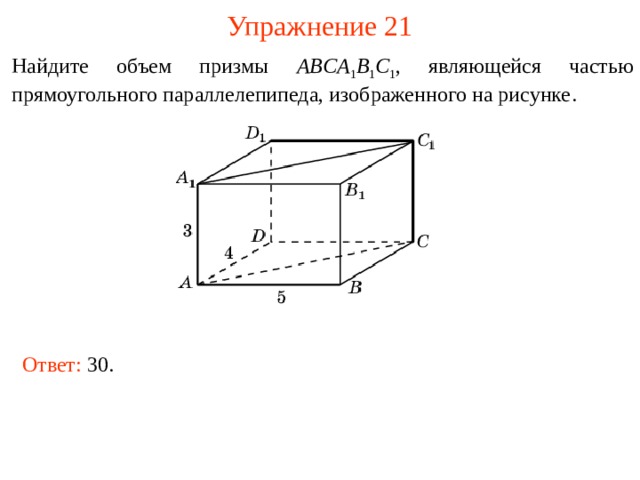
Упражнение 21
Найдите объем п ризмы ABCA 1 B 1 C 1 , являющейся частью прямоугольного параллелепипеда, изображенного на рисунке .
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 30 .
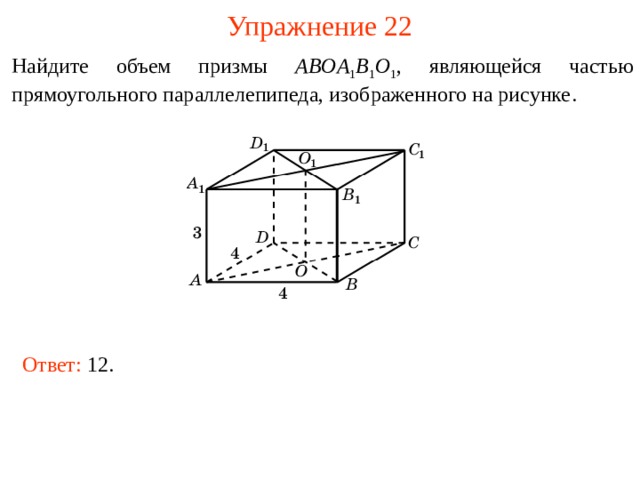
Упражнение 22
Найдите объем п ризмы ABOA 1 B 1 O 1 , являющейся частью прямоугольного параллелепипеда, изображенного на рисунке .
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 12.
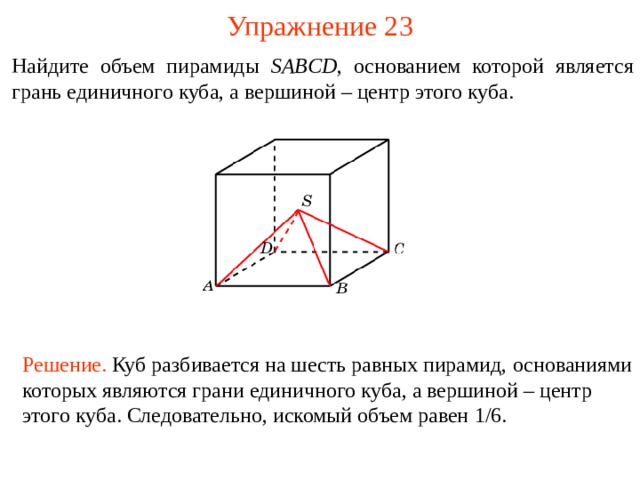
Упражнение 2 3
Найдите объем пирамиды SABCD , основанием которой является грань единичного куба, а вершиной – центр этого куба.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Решение. Куб разбивается на шесть равных пирамид, основани ями котор ых явля ю тся гран и единичного куба, а вершиной – центр этого куба . Следовательно, искомый объем равен 1/6.
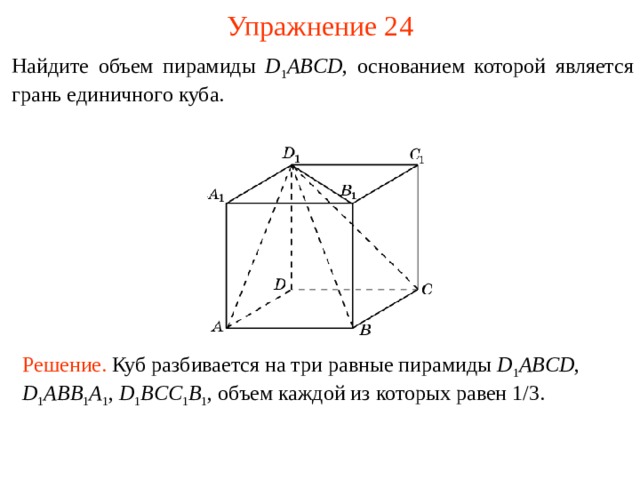
Упражнение 2 4
Найдите объем пирамиды D 1 ABCD , основанием которой является грань единичного куба.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Решение. Куб разбивается на три равные пирамиды D 1 ABCD , D 1 ABB 1 A 1 , D 1 BCC 1 B 1 , объем каждой из которых равен 1 /3.
26
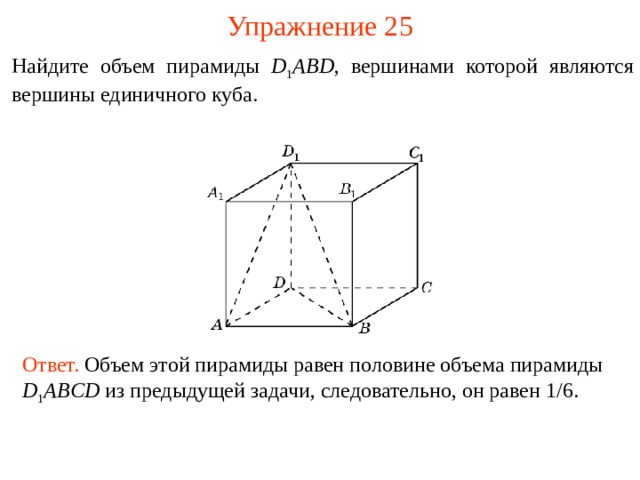
Упражнение 2 5
Найдите объем пирамиды D 1 ABD , вершинами которой явля ю тся вершины единичного куба.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ. Объем этой пирамиды равен половине объема пирамиды D 1 ABCD из предыдущей задачи, следовательно, он равен 1 / 6 .
ПЕРИМЕТР
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.
Чаще всего периметр обозначается буквой P.
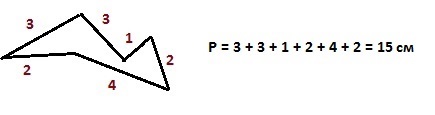
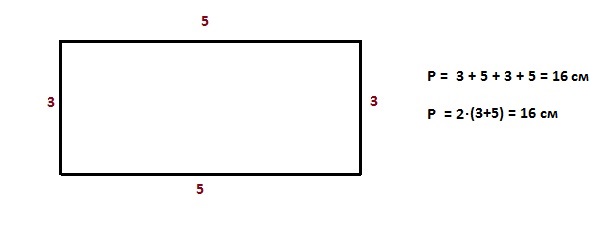
Периметр прямоугольника – удвоенная сумма длины и высоты – 2∙(a+b)
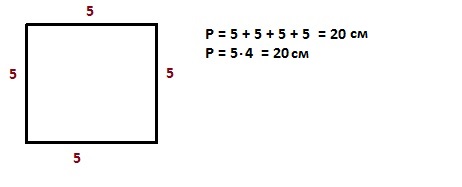
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.
ПЛОЩАДЬ
Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.
В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.
Чаще всего площадь обозначается буквой S.
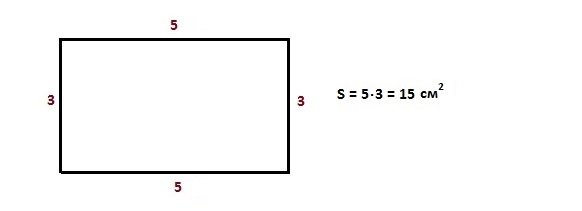
Площадь прямоугольника – произведение длины на высоту.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Разделим этот прямоугольник на квадраты
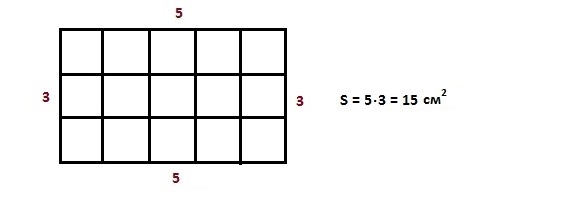
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.
Площадь квадрата – произведение длины стороны на саму себя.
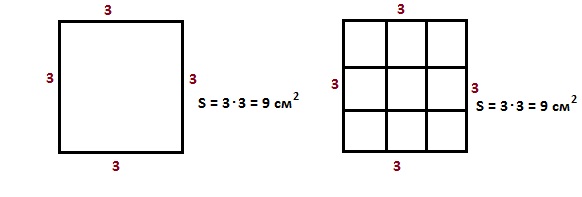
СОСТАВНЫЕ ФИГУРЫ
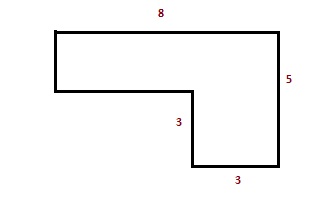
Разделим эту фигуру на прямоугольник и квадрат
Высота прямоугольника составит 5 – 3 = 2
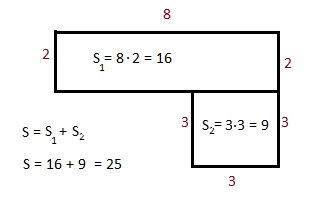
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА
Фигуры с одной и той же площадью могут иметь разный периметр
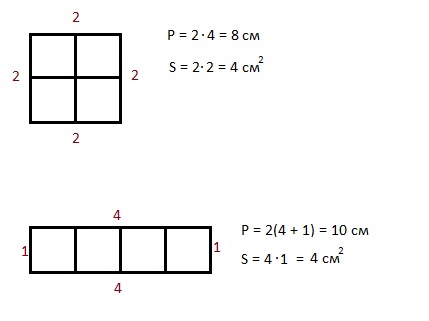
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?
Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.
Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.
ОБЪЁМ
Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.
1 л = 1 дм3
Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.
Чаще всего объём обозначается буквой V.
Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.
Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты

Зная объём и две стороны, мы можем найти третью сторону:
c = (V:a):b = V:S
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
ЗАДАЧИ
Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.
x = 10 см – ширина
1. Найдём длину
y = 10 + 6 = 16 см
2. Найдём периметр
P = 2∙(10+16) = 52 см
3. Найдём площадь
S = 10∙16 = 160 см2
Ответ: P = 52 см, S = 160 см2
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?
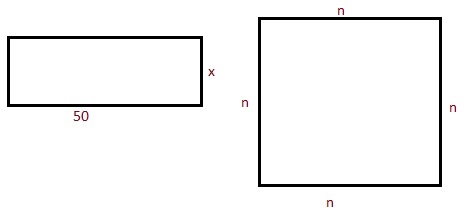
1. Вычислим сторону квадрата
4∙n = 80 – периметр
n = 20 см
2. Вычислим площадь квадрата
20∙20 = 400 см2
3. Вычислим ширину прямоугольника
50∙x = 400 см2
x = 8 см
Ответ: 8 см
Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?
1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм
1. Переведём длину прямоугольника в дм
x = 15∙10 = 150 дм
2. Найдём ширину прямоугольника
150∙y = 7500
y = 7500:150 = 50 дм
Ответ: 50 дм
Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.
1. Найдите площадь этого прямоугольника.
2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.
3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.
1. Найдём ширину прямоугольника
x = 60:3 = 20 см
2. Найдём площадь прямоугольника
S = 60∙20 = 1200 см
2. Найдём периметр прямоугольника
P = 2∙(60+20) = 160 см
3. Найдём сторону квадрата
y = 160:4 = 40 см
4. Найдём площадь квадрата
Sкв = 40∙40 = 1600 см2
5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:
Sкв2 = 1200:12 = 100 см2
6. Найдём сторону такого квадрата
Площадь квадрата = 100 см2
Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см
7. Найдём периметр такого квадрата
P = 10∙4 = 40 см
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.
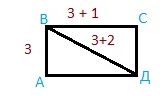
1. Найдём сторону ВС
ВС = 3+1 = 4
2. Найдём диагональ ВД
ВД = 3+2 = 5
3. Найдём периметр АВСД
P = 2∙(3+4) = 14 см
4. Найдём площадь АВСД
Sавсд = 3∙4 = 12 см2
5. Найдём периметр треугольника АВД
Pавд = 3 + 5 + 4 = 13 см
6. Найдём площадь треугольника АВД
Треугольник АВД занимает половину площади прямоугольника АВСД
Sавд = Sавсд:2
Sавд = 12:2 = 6 см2
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?
Решение
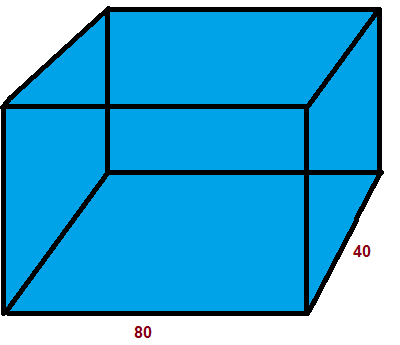
1. Переведём литры в кубические дециметры
1 л = 1 дм3, 160 л = 160 дм3
2. Переведём стороны аквариума в дециметры
1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм
3. Найдём высоту аквариума
V = a∙b∙c, a = 8, b = 4
c = (V:a):b
c = (160:8):4 = 5 дм
c = 5∙10 = 50 см
Ответ: 50 см



