Как найти объем фигуры ограниченной линиями онлайн

Как найти объем фигуры ограниченной линиями онлайн

Рассмотрим некоторую функцию
, непрерывную на отрезке
:

график некоторой функции f(x)

Если мы будем вращать данную функцию вокруг оси
, то образуется некоторое
тело вращения:

тело, полученное вращением функции f(x) вокруг оси х

Объём полученной фигуры можно посчитать, вычислив вот такой
интеграл:

Теперь рассмотрим некоторую функцию
, непрерывную на отрезке
:

график некоторой функции g(y)

На этот раз будем вращать данную функцию вокруг оси
. В результате получим следующее тело вращения:

тело, полученное вращением функции g(y) вокруг оси y

Его объём вычисляется по формуле:

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет вычислить объём тела вращения, заданного практически любой функцией. Для этого, в калькулятор нужно ввести саму функцию, границы в пределах которых будет вычисляться объём тела и выбрать ось вращения.

Источник

bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • объем:y=(3x+1)^{frac{1}{4}},:x=0,:x=8,:y=0

  • объем:y=sqrt{49-x^{2}},:y=0

  • объем:y=x+1,:y=0,:x=0,:x=2

  • объем:y=11e-x^{2},:y=0,:x=0,:x=1

  • объем:около:x=-1,:y=sqrt[3]{x},:y=1

  • Показать больше

Описание

Найдите объем тела вращения шаг за шагом

volume-calculator

объем y=(3x+1)^{frac{1}{4}}, x=0, x=8, y=0

ru

Блог-сообщения, имеющие отношение к Symbolab

  • My Notebook, the Symbolab way

    Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Вычислить объем тела, ограниченного поверхностями.

    Пример 1:

    Вычислить объем тела, ограниченного поверхностями (по площадям сечений).

    Решение от преподавателя:

    Строим графики функций:

    Тогда объем тела вращения вокруг оси будем находить по формуле:

    Ответ:.

    Пример 2:

    Найти объем тела, полученного вращением криволинейной трапеции вокруг оси ОХ.

    Решение от преподавателя:

    Пример 3:

    Решение от преподавателя:

    Пример 4:

    Вычислить объем тела, ограниченного поверхностями:

    Решение от преподавателя:

    Изобразим поверхность:

    то есть z меняется от

    Пример 5:

    Вычислить объемы тел, ограниченных поверхностями.

    Решение от преподавателя:

    Пример 6:

    Объем тела, ограниченного поверхностью, полученной от вращения дуги кривой  вокруг оси Ох.

    Решение от преподавателя:

    Объем фигуры, образованной в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной непрерывной кривой y = f(x) (a ≤ x ≤ b), Осью Ox и прямыми x= a и x = b, вычисляется по формуле:

    Построим график функции:

    Пример 7:

    Вычислить с помощью двойного интеграла объем тела, ограниченного указанными поверхностями:

    Решение от преподавателя:

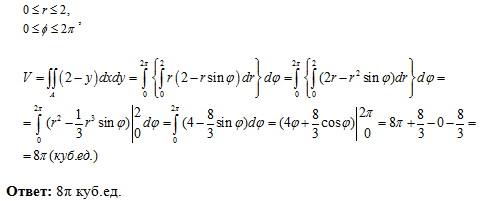
    Пример 8:

    Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми 

    Решение от преподавателя:

    Работа вам нужна срочно. Не волнуйтесь, уложимся!

    Заполните, пожалуйста, данные для автора:

    • 22423 авторов готовы помочь тебе.
    • 2402 онлайн
    Источник

    18:22

    Объем тела вращения

    Объем тела вращения

    Вычисление объема тела вращения вокруг оси Ох

    Пусть график функции y = f(x) вращается вокруг оси Ox, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями x = a, x = b.

    Объем тела вращения, образованного вращением графика y=f(x) вокруг оси Ox, может быть вычислен по формуле

    Пример 1. Вычислить объем тела, образованного вращением дуги кривой y=x2, x∈[1,3] вокруг оси Оx.

    Решение. Данные a=1, b=3,  f(x)=x2, подставляем в формулу, получаем

    С помощью калькулятора проверяем правильность вычисления объема , а также получаем рисунок тела вращения.

    Вычисление объема тела вращения вокруг оси Оy

    Пусть график функции x=φ(y) вращается вокруг оси Oy, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями y = c, y = d.

    Объем тела вращения, образованного вращением графика x=φ(y) вокруг оси Oy, может быть вычислен по формуле

    Пример 2. Вычислить объем тела, образованного вращением дуги кривой x=3y-y2, x∈[1,2] вокруг оси Оx.

    Решение. Данные c=1, d=2,  φ(y)=3y-y2, подставляем в формулу, получаем

    В калькулятор вставляем функцию x=3y-y2,  x меняем на y, границы  от 1 до 2, проверяем правильность вычисления объема , а также получаем рисунок тела вращения.

    Следующая тема: Вычислить длину кривой
    • 1
    • 2
    • 3
    • 4
    • 5

    Категория: Вычислить интеграл | Просмотров: 109978 | | Теги: приложение интегралов | Рейтинг: 3.6/17

    Источник

    Вычислить площадь фигуры, ограниченной линиями

    Данный калькулятор поможет найти площадь фигуры, ограниченной линиями.
    Для того чтобы вычислить площадь фигуры, ограниченной линиями, применяется одно из свойств интеграла. Это свойство аддитивности площадей, интегрируемых на одном и том же отрезке функции.

    Аддитивность означает, что площадь замкнутой области, составленных из нескольких фигур, не имеющих общих внутренних точек, равна сумме площадей этих фигур. Интеграл равен площади криволинейной трапеции, ограниченной графиками функций. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.
    Калькулятор поможет вычислить площадь фигуры ограниченной линиями онлайн.

    ×

    Пожалуйста напишите с чем связна такая низкая оценка:

    ×

    Для установки калькулятора на iPhone – просто добавьте страницу
    «На главный экран»

    Для установки калькулятора на Android – просто добавьте страницу
    «На главный экран»

    Источник

    Добавить комментарий