Как найти объем формуды - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Объём (значения).

Объём

Размерность	L³
Единицы измерения
СИ	м³
СГС	см³

Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей^[1].

Единица объёма в СИ — кубический метр; от неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.

В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

Вычисление объёма[править | править код]

На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.

Математически[править | править код]

Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром вычисляется с помощью выражения $V=a^{3}$ , а объём прямоугольного параллелепипеда — умножением его длины на ширину и на высоту.

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.

Сводка формул[править | править код]

Форма тела	Формула для вычисления объёма	Обозначения
Куб	${displaystyle V=a^{3};}$
Прямоугольный параллелепипед
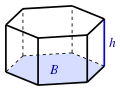
Призма (B: площадь основания)
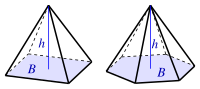
Пирамида (B: площадь основания)	${displaystyle V={frac {1}{3}}Bh}$
Параллелепипед	${displaystyle {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}}$
Тетраэдр	${displaystyle V={{sqrt {2}} over 12}a^{3},}$
Шар	${displaystyle V={frac {4}{3}}pi r^{3}}$
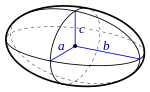
Эллипсоид	${displaystyle V={frac {4}{3}}pi abc}$
Прямой круговой цилиндр	${displaystyle V=pi r^{2}h}$
Конус	${displaystyle V={frac {1}{3}}pi r^{2}h}$
Тело вращения	${displaystyle V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x}$

Через плотность[править | править код]

Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: $V={frac {m}{rho }}$ .

Единицы объёма жидкости[править | править код]

1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона

Русские^[2][править | править код]

Ведро = 12,3 литра
Бочка = 40 вёдер = 492 литра

Английские[править | править код]

1 пинта = 0,568 литра
1 кварта (жидкостная) = 2 пинтам = 1,136 литра
1 галлон = 8 пинтам = 4,55 литра
1 галлон (амер.) = 3,785 литра

Античные[править | править код]

Котила = 0,275 литра

Немецкие[править | править код]

Шоппен

Древнееврейские^[3][править | править код]

Эйфа = 24,883 литра
Гин = 1/6 эйфы = 4,147 литра
Омер = 1/10 эйфы = 2,4883 литра
Кав = 1/3 гина = 1,382 литра

Единицы объёма сыпучих веществ[править | править код]

Русские[править | править код]

Четверик = 26,24 литра (1 пуд зерна)
Гарнец = 3,28 литра
Четверть = 1/4 ведра = 3,075 литра
Штоф = 1/8 ведра = 1,54 литра
Кружка = 1/10 ведра = 1,23 литра
Бутылка (винная) = 1/16 ведра = 0,77 литра
Бутылка (пивная) = 1/20 ведра = 0,61 литра
Чарка = 1/10 кружки = 0,123 литра
Шкалик (косушка) = 1/2 чарки = 0,0615 литра

Английские[править | править код]

1 бушель = 8 галлонов = 36,36872 литра
1 баррель = 163,65 литра

Прочие единицы[править | править код]

1 унция (англ.) = 2,841⋅10⁻⁵ м³
1 унция (амер.) = 2,957⋅10⁻⁵ м³
1 кубический дюйм = 1,63871⋅10⁻⁵ м³
1 кубический фут = 2,83168⋅10⁻² м³
1 кубический ярд = 0,76455 м³
1 кубическая астрономическая единица =3,348⋅10²⁴ км³
1 кубический световой год = 8,466⋅10³⁸ км³
1 кубический парсек = 2,938⋅10⁴⁰ км³
1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅10⁴⁹ км³

Примечания[править | править код]

↑ Математическая энциклопедия, 1982, с. 1149.
↑ Меры объёма в Древней Руси. Дата обращения: 17 ноября 2013. Архивировано 14 июля 2014 года.
↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4

Литература[править | править код]

Объём // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.

Объём // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Ссылки[править | править код]

Формулы объёма и программы для расчета объёма. Дата обращения: 26 ноября 2020. Архивировано 24 ноября 2020 года.

Источник

a – сторона куба

Формула объема куба, (V):

a, b, c – стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

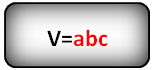
R – радиус шара

π ≈ 3.14

По формуле, если дан радиус, можно найти объема шара, (V):

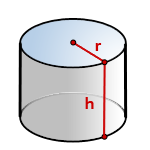
h – высота цилиндра

r – радиус основания

π ≈ 3.14

По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

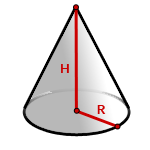
R – радиус основания

H – высота конуса

π ≈ 3.14

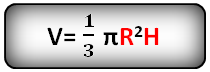
Формула объема конуса, если известны радиус и высота (V):

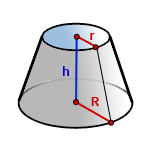
r – радиус верхнего основания

R – радиус нижнего основания

h – высота конуса

π ≈ 3.14

Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

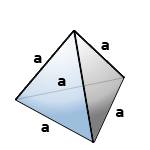
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.

а – ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

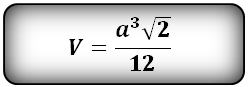
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

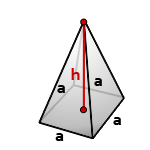
a – сторона основания

h – высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

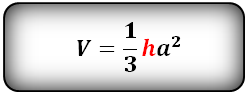
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

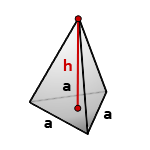
a – сторона основания

h – высота пирамиды

Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

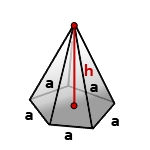
h – высота пирамиды

a – сторона основания пирамиды

n – количество сторон многоугольника в основании

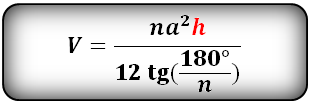
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

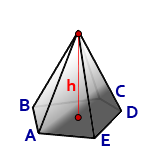
h – высота пирамиды

S – площадь основания ABCDE

Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):

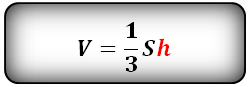
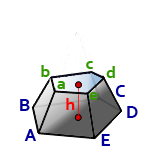
h – высота пирамиды

S_ниж – площадь нижнего основания, ABCDE

S_верх – площадь верхнего основания, abcde

Формула объема усеченной пирамиды, (V):

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара

h – высота сегмента

π ≈ 3.14

Формула для расчета объема шарового сегмента, (V):

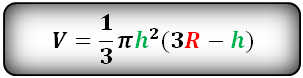
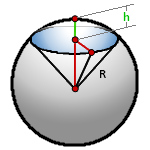
R – радиус шара

h – высота сегмента

π ≈ 3.14

Формула объема шарового сектора, (V):

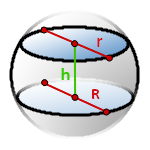
h – высота шарового слоя

R – радиус нижнего основания

r – радиус верхнего основания

π ≈ 3.14

Формула объема шарового слоя, (V):

Источник

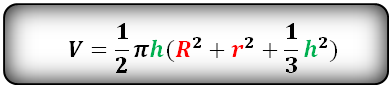
Формулы объема геометрических фигур

Объем геометрической фигуры

– количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Объем куба

Куб

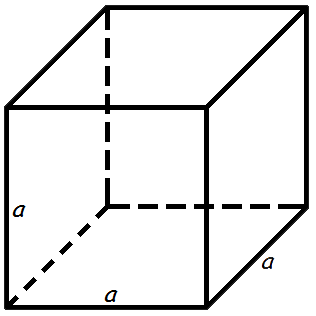
Объем куба равен кубу длины его грани.

Формула объема куба:

V = a³

где V – объем куба,

a – длина грани куба.

Объем призмы

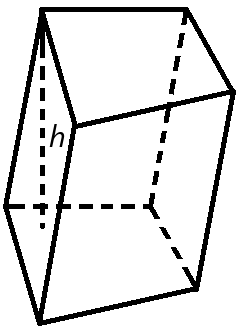
Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

V = S_o h

где V – объем призмы,

S_o – площадь основания призмы,

h – высота призмы.

Объем параллелепипеда

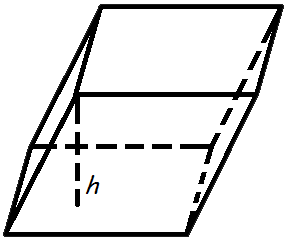
Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

V = S_o · h

где V – объем параллелепипеда,

S_o – площадь основания,

h – длина высоты.

Объем прямоугольного параллелепипеда

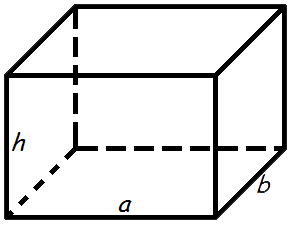
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

V = a · b · h

где V – объем прямоугольного параллелепипеда,

a – длина,

b – ширина,

h – высота.

Объем пирамиды

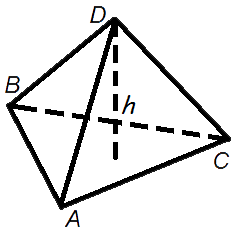
Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

где V – объем пирамиды,

S_o – площадь основания пирамиды,

h – длина высоты пирамиды.

Объем правильного тетраэдра

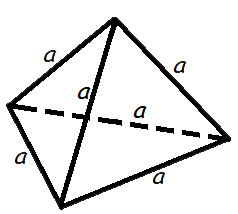
Формула объема правильного тетраэдра:

где V – объем правильного тетраэдра,

a – длина ребра правильного тетраэдра.

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра:

V = π R² h

V = S_o h

где V – объем цилиндра,

S_o – площадь основания цилиндра,

R – радиус цилиндра,

h – высота цилиндра,

π = 3.141592.

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

где V – объем конуса,

S_o – площадь основания конуса,

R – радиус основания конуса,

h – высота конуса,

π = 3.141592.

Объем шара

шар

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

Формула объема шара:

где V – объем шара,

R – радиус шара,

π = 3.141592.

Источник

Изучение объемных фигур начинается со школы. В это время происходит знакомство с цилиндром, параллелепипедом, шаром, конусом и другими геометрическими телами. Одна из главных задача, которая сопровождает учеников, это вычисление объема фигур. Оперируя формулами, удается произвести расчет и получить ответ в метрах кубических (м³).

Чтобы вычислить объем, применяйте следующее правило – длину, ширину и высоту нужно перемножить между собой. Объем для каждой фигуры рассчитывается по специальной формуле, о которых, мы расскажем ниже.

Подписывайтесь на наш Telegram — канал

Содержание:

Как найти объем трехмерных объектов
Как найти объем для фигур цилиндрической формы
Как рассчитать объем треугольной пирамиды
Как посчитать объем куба
Как найти объем прямоугольного параллелепипеда
Как найти объем цилиндра
Как найти объем пирамиды

Как найти объем трехмерных объектов

Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.

Измеряем длину предмета в сантиметрах – 9. Сантиметры приходят на помощь, когда невозможно получить целое число в метрах .
Замеряем ширину в сантиметрах – 17.
Умножаем между собой длину и ширину 9 * 17 = 152 см²– получили площадь основания
Производим замер высоты – 28 см.
Умножаем площадь основания на высоту 152 см²* 28 см = 4256.

Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м³/1000000 = 0,004256 м³

Как найти объем для фигур цилиндрической формы

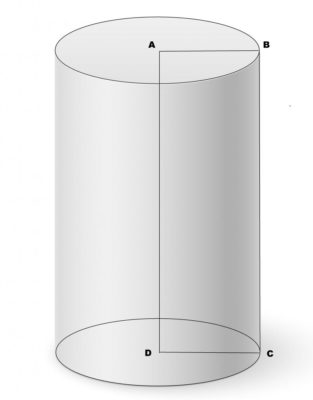
Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.

Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.

Производим расчеты: 30 см / 2 = 15 см. Половина диаметра круга ‒ радиус.
Возводим полученный радиус в квадрат или умножаем самого на себя: 15 * 15 = 225 см².
Полученное число 225 см² – это квадрат радиуса. Эту цифру умножаем на число ПИ — 3,14. Например: 225 см²* 3,14 = 706,5 см².
Проводим новый замер, чтобы узнать расстояние между круглыми основаниями, допустим, оно равно 12 см.
Это число умножаем на площадь круглого основания: 706,5 см²* 12 см = 8 478 см³
Полученное значение и будет искомым объемом. Для перевода в кубические метры необходимо конечное число поделить на один миллион. Как мы делали в предыдущем примере.

Как рассчитать объем треугольной пирамиды

Пирамида – это многогранник, где есть одна грань основания и боковые грани. Пирамиды бывают треугольные, четырехугольные и другие. Также есть правильная и усеченная пирамида. Объем для каждой фигуры рассчитывается по разным формулам.

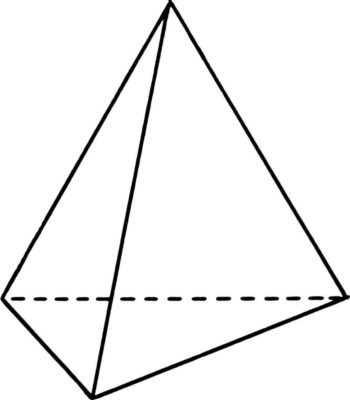
Чтобы найти объём пирамиды замеряем длину стороны треугольника в основании пирамиды, предположим, что он равен 10 см.
Затем повторим то же самое, но с высотой – 13 см.
Длину высоты и стороны необходимо перемножить между собой и разделить на 2: 10 *13 = 130 см²/ 2 =65 см².
Замеряем высоту пирамиды – 33 см.
Умножаем площадь треугольника у основания на высоту и делим на 3. Например: 65 см²* 33 см =2 145 см²/ 3 = 715 см³.
Для преобразования в кубические метры производим деление конечного числа на миллион.

Расчёт четырехгранной пирамиды производится тем же принципом. Потренируйтесь, используя разные задачи. Чтобы все замеры происходили правильно, не забудьте обзавестись хорошей линейкой, также на помощь придёт калькулятор, который поможет перемножать числа между собой.

В интернете представлено много онлайн-калькулятор, они дают подсказку и позволяют без лишних трудностей рассчитать объём куба, цилиндра и других фигур. Перед началом пользования таких подсказок, необходимо обладать базовыми знаниями, чтобы быстрее разобраться в полученном результате.

Как посчитать объем куба

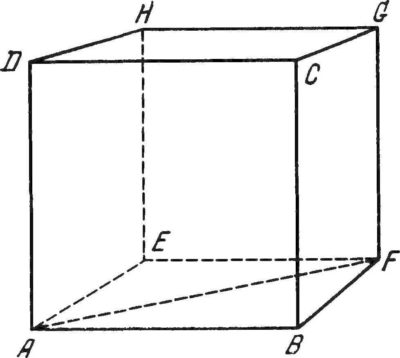
Параллелепипед складывается из шести граней, которые являются параллелограммом. Все противоположные грани попарно равны и параллельны. Фигура получилась 4 диагонали, и все они пересекаются в одной точке, разделяют эту точку пополам. Параллелепипед, грани которого являются квадратами, будет называться кубом.

Все рёбра куба всегда будут равны. Для проведения вычислений, воспользуйтесь следующей формулой V = H³, где H ‒ высота ребра куба. Например: высота куба равняется ‒ 3 см, получается, что объем равен 3³= 27 см³.

Как найти объем прямоугольного параллелепипеда

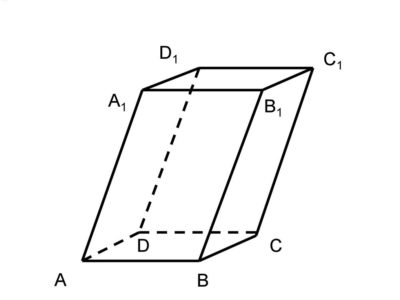
Прямоугольным параллелепипедом называется фигура, у которой все шесть граней прямоугольники. Для вычисления работает следующая формула:

V = SH = abc

Где H ‒ высота, S ‒ площадь основания, abc – ребра. Чтобы произвести расчеты и найти объём, необходимо узнать произведение площади основания на высоту. Например: 1 см * 2 см * 3 см = 6 см³

Советы по измерению:

Измерить стороны.
Каждая сторона параллелепипеда должна находиться в одинаковых единицах измерения.
Вычисляем площадь основания.
Умножаем площадь основания на высоту параллелепипеда.

Убедитесь, что перед вами параллелепипед, а не куб, так как в случае с кубом расчетная формула будет проще.

Как найти объем цилиндра

Цилиндр считать круглой фигурой, т.к. в его основании лежит круг. Чтобы произвести вычисления, необходимо узнать произведение площади основания на высоту. Для этого используется следующая формула:

V= π * r² * h

Где r ‒ радиус цилиндра, h – высота цилиндра. Чисто π – является константой и равно 3,14. Оно всегда одинаковое и не требует никаких измерений. Рассмотрим на примере:

3,14 * 2 см²* 5 см = 62.831853071796 = 63см³

Если вы не можете вычислить радиус, измерьте диаметр с помощью формулы преобразования.

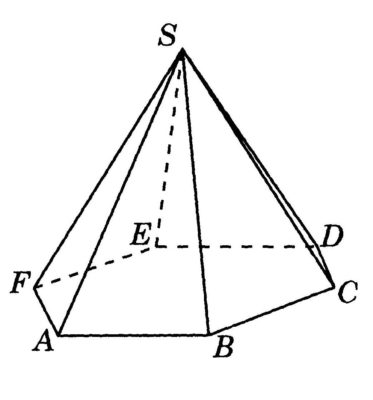
Как найти объем пирамиды

фото 6 — посчитать объём

Чтобы произвести расчет объема, нам нужно найти произведение площади основания на высоту. Для вычисления используется следующая формула:

V = S*h

Где S (A*B*C*D*E) – площадь основания пирамиды, а h ‒ высота пирамиды. Рассмотрим на примере:

V = 3 * 2 = 2 см³‒ это и будет являться объемом искомой геометрической фигуры.

Не забывайте, что пирамиды бывают усеченные, правильные, трех- и четырехугольные. Для каждого тела действуют свои расчеты, но важно начинать с основного и не упускать базовые знания, в дальнейшем все примеры будут базироваться именно на них.

Если какая-то формула осталась непонятной, лучше вернуться к этому и поупражняться ещё раз, доведя знание до автоматизма. Так решение задач не будет вызывать сложности. Постоянная практика ‒ это основа успешного результата.

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	$V=S_text{OCH}h, h -$ высота
Прямоугольный параллелепипед		$d=sqrt{a^2+b^2+c^2}$
Призма	$V=S_text{OCH}h$	$S = 2S_text{OCH}+$
Пирамида	$V=frac{1}{3}S_text{OCH}h$	$S = S_text{OCH}+$

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше – читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

$P_text{OCH}=8+6+6+2+2+4=28.$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник), $S_text{OCH}=36+8=44$

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

$P_text{OCH}=4+5+2+1+2+4=18.$

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), $S_text{OCH}=16+2=18$ (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда $angle{ABC}=120^{circ}$

Из по теореме косинусов найдем ребро АС:

$AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}$

$AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7$

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда h=5.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

$AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.$

Из прямоугольного имеем:

$DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.$

(по двум катетам), тогда $S_{ADB}=S_{ADC},$ следовательно

$=2S_{ADB}+S_{BDC},$ $=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.$

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани – равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h – апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

$h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35$

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен $V=S_{OCH}cdot h$ , а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

$S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.$

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен $V = S_{OCH}cdot h$

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды ABDA_1.

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

$=S_{ABCD}cdot A_1H$

$=frac{1}{3}S_{ABD}cdot A_1H$

Диагональ основания делит его на два равных треугольника, следовательно, $S_{ABD}=frac{1}{2}S_{ABCD}.$

Имеем:

$ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.$

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна $S_{OCH}=frac{a^2sqrt{3}}{4}.$

$S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.$

Объем пирамиды $V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.$

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда $S_{OCH}=x^2.$

Так как точки М и К – середины АD и DС соответственно, то $DM=DK=frac{x}{2}.$

$S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.$

Площадь треугольника MDK, лежащего в основании новой призмы, составляет $frac{1}{8}$ часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: $V=S_{OCH}cdot h$ , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

$S=P_{perp}cdot l.$

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Вычисление объёма[править | править код]

Математически[править | править код]

Сводка формул[править | править код]

Через плотность[править | править код]

Единицы объёма жидкости[править | править код]

Русские[2][править | править код]

Английские[править | править код]

Античные[править | править код]

Немецкие[править | править код]

Древнееврейские[3][править | править код]

Единицы объёма сыпучих веществ[править | править код]

Русские[править | править код]

Английские[править | править код]

Прочие единицы[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Формулы объема геометрических фигур

Объем куба

Объем призмы

Объем параллелепипеда

Объем прямоугольного параллелепипеда

Объем пирамиды

Объем правильного тетраэдра

Объем цилиндра

Объем конуса

Объем шара

Содержание:

Как найти объем трехмерных объектов

Как найти объем для фигур цилиндрической формы

Как рассчитать объем треугольной пирамиды

Как посчитать объем куба

Как найти объем прямоугольного параллелепипеда

Как найти объем цилиндра

Как найти объем пирамиды

Формулы объёма и площади поверхности. Многогранники.

Вам также может понравиться

Как можно исправить прокисший суп

Как составить анализ по заработной плате

Как найти сороку в лесу

Добавить комментарий Отменить ответ

Русские^[2][править | править код]

Древнееврейские^[3][править | править код]