Как найти объем газа по графику - Сайт, где вы сможете решить свои вопросы

Изопроцессы

Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
Изотермический процесс
Графики изотермического процесса
Изобарный процесс
Графики изобарного процесса
Изохорный процесс
Графики изохорного процесса

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.

На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:

• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;

• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).

Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.

Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).

Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.

Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.

1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .

Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.

к оглавлению ▴

Изотермический процесс

Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.

Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:

$p_1V_1=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT,$

$p_2V_2=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT.$

Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.

Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:

(1)

Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:

(2)

Данное утверждение называется законом Бойля — Мариотта.

Записав закон Бойля — Мариотта в виде

$p=frac{displaystyle const}{displaystyle V vphantom{1^a}},$ (3)

можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.

Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.

к оглавлению ▴

Графики изотермического процесса

Вообще, графики термодинамических процессов принято изображать в следующих системах координат:

• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .

График изотермического процесса называется изотермой.

Изотерма на -диаграмме — это график обратно пропорциональной зависимости $p=frac{displaystyle const}{displaystyle V vphantom{1^a}}$ .

Такой график является гиперболой (вспомните алгебру — график функции $y=frac{displaystyle k}{displaystyle x vphantom{1^a}}$ ). Изотерма-гипербола изображена на рис. 1.

Рис. 1. Изотерма на -диаграмме

Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на –диаграмме.

В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2). Первый процесс идёт при температуре T_1 , второй — при температуре T_2 .

Рис. 2. Чем выше температура, тем выше изотерма

Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление p_1 , на второй — . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, .

В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):

Рис. 3. Изотермы на и -диаграммах

к оглавлению ▴

Изобарный процесс

Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.

Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно

$p=p_0 + frac{displaystyle Mg}{displaystyle S vphantom{1^a}},$

где p_0 — атмосферное давление.

Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .

Выпишем уравнения состояния:

$pV_1=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_1,$

$pV_2=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_2.$

Поделив их друг на друга, получим:

$frac{displaystyle V_1}{displaystyle V_2 vphantom{1^a}}=frac{displaystyle T_1}{displaystyle T_2 vphantom{1^a}}.$

В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):

$frac{displaystyle V_1}{displaystyle T_1 vphantom{1^a}}=frac{displaystyle V_2}{displaystyle T_2 vphantom{1^a}}.$ (4)

А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:

$frac{displaystyle V}{displaystyle T vphantom{1^a}}=const.$ (5)

Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:

(6)

Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.

к оглавлению ▴

Графики изобарного процесса

График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4):

Рис. 4. Изобара на -диаграмме

Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.

Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на –диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями p_1 и p_2 (рис. 5):

Рис. 5. Чем ниже изобара, тем больше давление

Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).

Стало быть, .

В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):

Рис. 6. Изобары на и -диаграммах

к оглавлению ▴

Изохорный процесс

Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.

Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).

Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:

$p_1V=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_1,$

$p_2V=frac{displaystyle m}{displaystyle mu vphantom{1^a}}RT_2.$

Делим эти уравнения друг на друга:

$frac{displaystyle p_1}{displaystyle p_2 vphantom{1^a}}=frac{displaystyle T_1}{displaystyle T_2 vphantom{1^a}}.$

Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:

$frac{displaystyle p_1}{displaystyle T_1 vphantom{1^a}}=frac{displaystyle p_2}{displaystyle T_2 vphantom{1^a}}.$ (7)

Ввиду произвольности выбора состояний мы приходим к закону Шарля:

$frac{displaystyle p}{displaystyle T vphantom{1^a}}=const.$ (8)

Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:

(9)

Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.

к оглавлению ▴

Графики изохорного процесса

График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7):

Рис. 7. Изохора на -диаграмме

Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.

Далее, чем больше объём, тем ниже идёт изохора на –диаграмме (рис. 8):

Рис. 8. Чем ниже изохора, тем больше объём

Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, .

В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):

Рис. 9. Изохоры на и -диаграммах

Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.

Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Изопроцессы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На диаграмме представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?

На диаграмме (см. рис.) представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3?

Пройти тестирование по этим заданиям

Источник

М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург

Графические задачи на газовые
законы

Графические
задачи заслуживают особого внимания, ибо, как
показывает опыт, они представляют наибольшую
трудность для абитуриентов. Причина проста:
этому типу задач в школьном курсе уделяют
неоправданно мало внимания – решают одну-две
задачи, притом формально, не вникая в суть. Кроме
того, в школе ограничиваются изопроцессами,
когда масса газа постоянна. Именно поэтому на
вступительных экзаменах абитуриенты теряются и
не знают даже, с чего начать и каковы методы
решения.

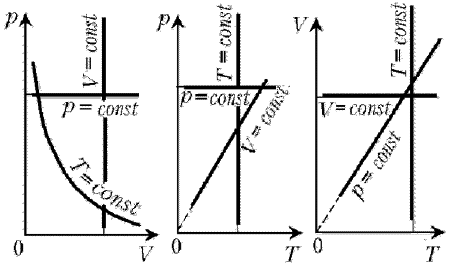
Напомним, как изображаются на диаграммах
изотерма, изобара и изохора идеального газа.

Можно выделить несколько типов графических
задач. В задачах первого типа графически
задается какой-то изопроцесс в явной или неявной
форме. Для решения таких задач можно предложить
следующий «план действий»:

1. Установить характер изображенного процесса
(если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из
изопроцессов и изобразить его графически
(провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с
линией (или с линиями) представленного процесса
(или процессов).
4. Спроецировать точку (или точки) пересечений
этих линий на одну из координатных осей (выбор
оси произволен).
5. Рассмотреть состояния данной массы газа,
которым соответствуют эти проекции, и, используя
известные газовые законы, ответить на
поставленный в задаче вопрос.

Проиллюстрируем этот алгоритм примерами.

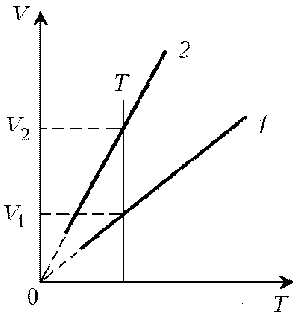Пример
1. Какая из двух линий графика соответствует
большему давлению данной массы идеального газа?

Решение. Прежде всего установим, что это за
линии. Эти линии выражают прямо пропорциональную
зависимость между объемом газа и его
температурой, а это возможно для идеального газа
только при изобарическом процессе,
следовательно, изображенные линии графика –
изобары.

Проведем изотерму до пересечения с обеими
изобарами, а точки их пересечения спроецируем на
ось ординат (объемов). Из построения видно, что V₂
> V₁. Поскольку при изотермическом
процессе газ подчиняется закону Бойля–Мариотта:
р₁V₁ = р₂V₂, то р₁ > р₂.
Напомним, что все точки, лежащие на одной изобаре,
соответствуют состояниям с одинаковым
давлением.

Читателю предоставляется возможность решить
эту задачу путем построения изохоры и
проецирования точек пересечения на ось
температур (еще раз стоит напомнить, что выбор
способа решения в задачах данного типа
произволен).

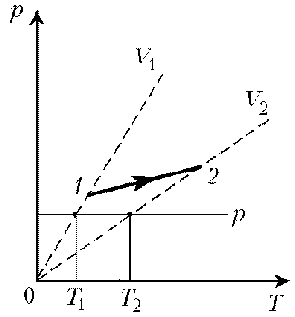
Пример
2. При нагревании идеального газа постоянной
массы получена зависимость р(T) при переходе из
состояния 1 в состояние 2. Как при этом переходе
менялась плотность газа?

Решение. Прежде всего обратим внимание на то,
что линия графика не описывается ни одним из
изопроцессов («неявная форма»).

Проведем через начальную и конечную точки
линии графика две изохоры.

Проведя еще изобару (или, как вариант, изотерму)
и, спроецировав точки ее пересечения с изохорами
на ось Т, убедимся, что Т₂ > Т₁. При
изобарическом процессе, по закону Гей-Люссака, V ~
T, следовательно, V₂ > V₁. А т.к.
плотность и объем связаны обратной зависимостью
(при данной массе), то r₁ > r₂, откуда следует, что газ
расширялся, а значит, его плотность уменьшилась.

В задачах второго типа в условии задан некий
цикл, совокупность процессов, в результате
которых данная масса газа возвращается в
исходное состояние. Этот цикл может быть задан на
разнообразных диаграммах: p, V; p, T; V, T и др. Как
правило, в таких задачах требуется представить
заданный цикл на других диаграммах. Эти задачи
важны при рассмотрении первого закона
термодинамики, когда совершается
макроскопическая работа и происходит процесс
теплообмена. Важно понимать, что цикл – это
замкнутый процесс, и он должен быть замкнутым на
любой диаграмме!

При решении предлагается следовать следующему
алгоритму:

1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между
собой величины).
4. По графику выяснить, как меняется каждая
величина.

Условимся для удобства обозначать ход процесса
стрелками: – увеличение величины, Ї –
уменьшение величины.

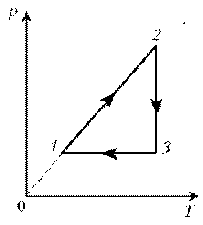
Пример
3. На диаграмме р, T изображен цикл идеального газа
постоянной массы. Изобразите его на диаграмме р,
V.

Решение. Проведем поэтапный анализ
представленного цикла:

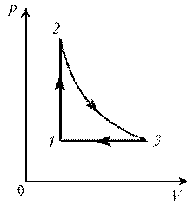1–2:
изохорический процесс; закон Шарля; р ~ T; р, T.

2–3: изотермический процесс; закон
Бойля–Мариотта; р ~ 1/V; рЇ; V

3–1: изобарический процесс; закон Гей-Люссака; V ~
T; TЇ; VЇ.

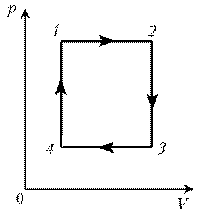
Теперь результаты поэтапного анализа
перенесем на диаграмму р, V.

Пример
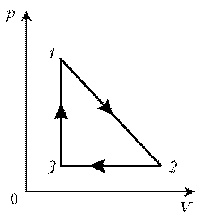
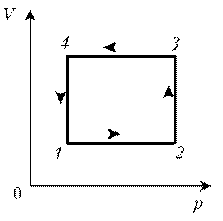
4. Для постоянной массы идеального газа
представлен цикл на диаграмме р, V. Изобразить
этот цикл на диаграмме V, T.

Решение. Проведем поэтапный анализ:

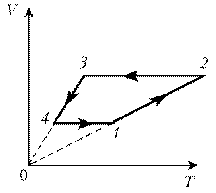1–2:
изобарический процесс; закон Гей-Люссака; V~ T; V; T.

2–3: изохорический процесс; закон Шарля; р~ T; рЇ; TЇ.

3–4: изобарический процесс; закон Гей-Люссака; V ~
T; VЇ; TЇ.

4–1: изохорический процесс; закон Шарля; р ~ T; р; T.

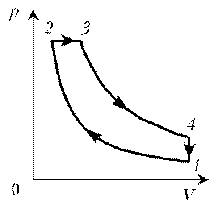Пример
5. Изобразите на диаграмме р, Т цикл постоянной
массы идеального газа, представленный на
диаграмме р, V.

Решение

1–2: изотермический процесс; закон
Бойля–Мариотта; р ~ 1/V; р; VЇ

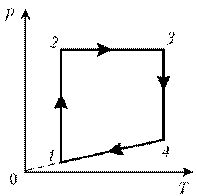2–3:
изобарический процесс; закон Гей-Люссака; V~T; V; T

3–4: изотермический процесс; закон
Бойля–Мариотта; р ~ 1/V; рЇ; V

4–1: изохорический процесс; закон Шарля; р ~ T; рЇ; TЇ.

А вот блок задач с необычной постановкой
условия. Впрочем, и они решаются достаточно
стандартными методами, а известные формулы
начинают играть новыми красками. Давайте
убедимся в этом.

Пример
6. Как менялась температура постоянной
идеального массы газа на протяжении цикла? Точки
1 и 2 лежат на одной изотерме.

Решение. Проведем изотермы через характерные
точки 1, 2, 3 и касательную к участку 1–2. Как
следует из теории, изотермы, более удаленные от
координатных осей, соответствуют более высоким
температурам. В этом можно убедиться, используя
методы, предложенные в предыдущих задачах.

Проходим по циклу:

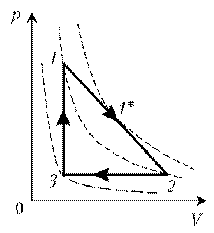1–1*:
переход на более «высокую» изотерму, значит,
температура растет.

1*–2: переход на более «низкую» изотерму,
следовательно, температура понижается.

2–3: переход на еще более «низкую» изотерму, это
означает дальнейшее понижение температуры.

3–1: переход на более «высокую» изотерму,
значит, температура повышается.

Как видим, ничего необычного в этой задаче нет,
при решении использованы известные факты.

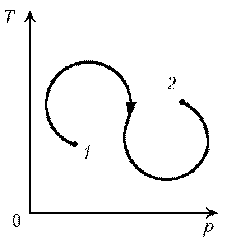Пример
7. Как менялась плотность идеального газа
постоянной массы при переходе 1–2?

Решение. Проведем изохоры через характерные
точки 1, А, В, 2. Проведем изотерму, пересекающую
все изохоры, и спроецируем эти точки пересечения
на ось р. Плотность r = m/V, т.е. плотность обратно
пропорциональна объему. При 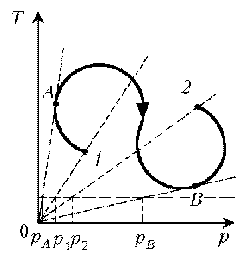изотермическом
процессе р ~ 1/V. Таким образом, задача сводится к
вопросу, каким изохорам соответствуют большие
или меньшие объемы. Обратимся к графику:

1–А: р₁ > р_A Ю V₁
< V_A Ю r₁
> r_А Ю rЇ.

А–В: р_В > р_А Ю V_В
< V_А Ю r_В
> r_А Ю r

В–2: р_В > р₂ Ю V_В
< V₂ Ю r_В
> r₂ Ю rЇ

Итак, сначала плотность уменьшается, затем
увеличивается и снова уменьшается.

А это уже пример задачи, в которой «играют»
формулы, позволяющие получить ответ, казалось бы,
без конкретных данных.

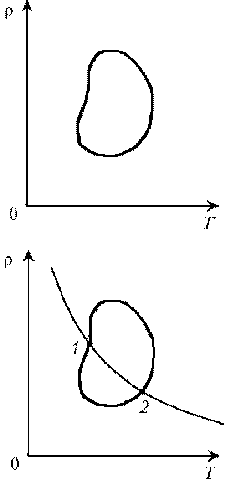Пример
8. Дан цикл идеального газa постоянной массы.
Указать в этом цикле пару точек равного давления.

Решение. В наших руках есть надежное «оружие» в
виде уравнения Клапейрона–Менделеева! Применим
его для двух произвольных состояний, учитывая,
что в этих состояниях, по условию, давления
одинаковы. Выразим объем через массу и плотность:
V = m/r. Тогда:

р₁V₁ = р₁m/r₁
= nRT₁;

р₂V₂ = p₂ m/r₂
= nRT₂.

Теперь остается разделить одно уравнение на
другое:

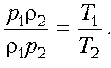
Но р₁ = р₂, значит, r₁T₁
= r₂T₂, или rT
= const, или r ~ 1/T.

Как известно, обратно пропорциональная
зависимость изображается гиперболой. Точки ее
пересечения с циклом и будут соответствовать
состояниям с одинаковым давлением. Заметим:
любые другие гиперболы, пересекаясь с линией
графика, будут давать пары состояний с
одинаковым (но уже другим) давлением.

И в заключение рассмотрим три примера, о
которых говорилось выше, – задачи, в которых
масса газа меняется. К сожалению, как правило,
подобные задачи в школьном курсе не
рассматриваются. Это и приводит к неприятностям
на вступительных экзаменах: срабатывает «фактор
неожиданности», и абитуриент теряется…

Пример
9. Идеальный газ с молярной массой М участвует в
изотермическом процессе. При этом получена
зависимость между объемом V и давлением р.
Представьте этот цикл на диаграмме V, m.

Решение. Запишем уравнение
Клапейрона–Менделеева:

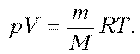
По
условию, T, M и R – постоянные, следовательно, m ~ рV.

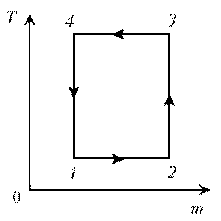
Рассмотрим процессы цикла поэтапно:

1–2: T = const, V = const; m ~ р; р; m

2–3: T = const, р = const; m ~ V; V; m

3–4: T = const, V = const; m ~ р; pЇ; mЇ

4–1: T = const, р = const; m ~ V; VЇ; mЇ

Пример
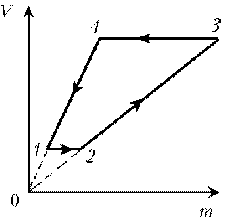
10. Идеальный газ с молярной массой М совершает
изобарический процесс, что отражено на
представленной диаграмме T, m. Изобразите этот
цикл на диаграмме V, m.

Решение. Запишем уравнение

Клапейрона–Менделеева: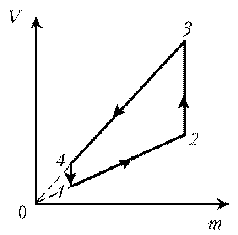

1–2: р = const; T = const; V ~ m; m; V.
2–3: р = const; m = const; V ~ T; T; V.
3–4: р = const; T = const; V ~ m; mЇ; VЇ
4–1: р = const; m = const; V ~ T; TЇ; VЇ.

Легко видеть, что ничего «необычного» в этих
задачах нет, они решаются все теми же методами,
которые рассматривались выше. Хочется надеяться,
что после знакомства с ними у школьников и
абитуриентов проблем уже не будет.

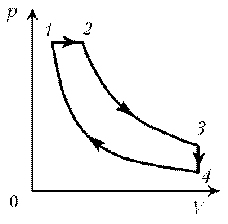Пример
11. Дан график зависимости р(V) для процессов,
проводимых с идеальным газом неизменного
химического состава при постоянной температуре.
Кривые 2–3 и 4–1 – гиперболы. Изобразите эти
процессы в координатах m, р.

Решение. Запишем уравнение
Клапейрона–Менделеева: .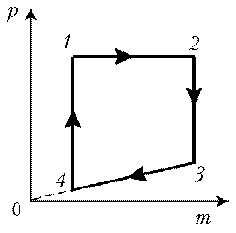

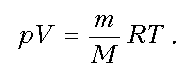
1–2: T = const, р = const; V ~ m; V; m

2–3: T = const, р ~ 1/V; m = const; рЇ

3–4: T = const, V = const; р ~ m; pЇ; mЇ

4–1: T = const, р ~ 1/V; m = const; р

Задачи для самостоятельного решения

1. Изобразите цикл постоянной массы идеального
газа на диаграммах V, T; р, V.

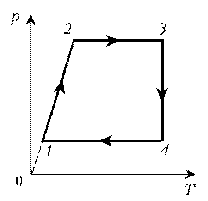
2. Изобразите цикл постоянной массы идеального
газа на диаграммах р, T; р, V.

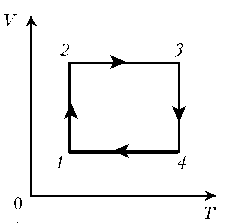
3. Как менялась плотность постоянной массы
идеального газа при переходе 1–2?

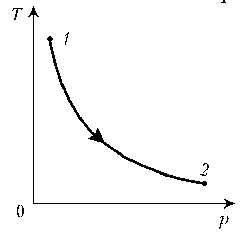
4. Изобразите цикл постоянной массы идеального
газа на диаграммах р, V и р, T.

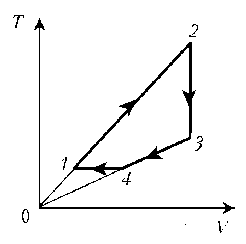
5. Идеальный газ постоянной массы расширяется по
закону рV² = const. Как при этом меняется
температура газа: повышается или понижается?

6. Как менялась температура постоянной массы
газа при переходе 1–2?

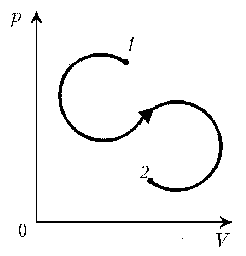
7. Дан цикл постоянной массы идеального газа.
Указать на линии графика состояния, которым
соответствуют экстремальные значения
температуры.

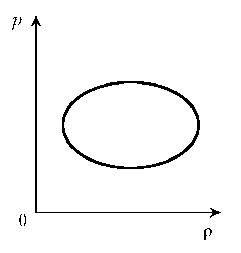
8. Над постоянной массой идеального газа
совершается работа по представленному циклу.
Найти отношение экстремальных значений объема в
цикле и изобразить цикл на диаграммах р, V; V, T.

Источник

Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»

Подробности: Обновлено 13.08.2018 14:05; Просмотров: 712

«Физика – 10 класс»

При решении многих задач на газовые законы требуется построение графиков, изображающих разного рода процессы. На графиках обозначаем точки, определяющие состояния системы. Имеем в виду, что можно изобразить только равновесные процессы, при которых каждое промежуточное состояние равновесное, т. е. температура и давление одинаковы во всех точках данного объёма.

Задача 1.

Постройте изобары для водорода массой 2 г при нормальном атмосферном давлении р₀ в координатах р, Т; р, V; V, Т.

Р е ш е н и е.

На графиках зависимости р от Т и р от V изобара представляет собой прямую, параллельную либо оси Т, либо оси V (рис. 10.5, а и б). Так как то графиком зависимости V от Т является прямая, проходящая через начало отсчёта. Учитывая, что m = 0,002 кг, М = 0,002 кг/моль, R = 8,31 Дж/(моль • К) и р₀ = 10⁵ Па, можно записать: V = ВТ, где В частности, при Т = 100 К V ≈ 8 • 10^-3 м³. График зависимости V от Т показан на рисунке (10.5, в).

Задача 2.

Выведите уравнение Клапейрона при переходе газа из состояния 1 (Р₁, V₁, Т₁) в состояние 2 (р₂, V₂, Т₂) (рис. 10.6, а).

Р е ш е н и е.

Переведём газ из состояния 1 в состояние 2, совершив два процесса: изотермический из состояния 1 в состояние 1′, поддерживая постоянную температуру T₁, и изобарный из состояния 1′ в состояние 2, поддерживая постоянным давление р₂ (рис. 10.6, б).

Согласно закону Бойля—Мариотта запишем: P₁V₁ = p₂V’, согласно закону Гей-Люссака Выразив из первого и второго уравнений V’ и приравняв правые части полученных равенств, запишем:
Перенеся параметры с индексом 1 в левую часть, а параметры с индексом 2 в правую, получим уравнение Клапейрона Для вывода уравнения мы использовали два экспериментально установленных закона: изотермический и изобарный.

Задача 3.

На графике (рис. 10.7) показан переход газа, взятого в количестве 2 моль, из состояния А в состояние В. Определите изменение температуры газа, а также максимальное значение температуры при этом переходе.

Р е ш е н и е.

По графику видно, что сначала газ нагревался при постоянном давлении, а затем давление уменьшалось при постоянном объёме, при этом температура уменьшалась. Обратим внимание на то, что произведение давления на объём в состояниях А и В одно и то же и равно 4000 Па • м³.

Согласно закону Менделеева—Клапейрона ΔТ = 0.

Начертим изотермы, проходящие через отмеченные состояния. Согласно графикам максимальная температура соответствует промежуточному состоянию 1′, для которого V = 4 л, а давление 4 • 10⁶ Па. Тогда Т = 962 К.

Задача 4.

На рисунке (10.8, а) изображён график перехода газа из состояния А в состояние В в координатах р, V. Постройте график этого перехода в координатах р, Т и V, Т.

Р е ш е н и е.

Сначала построим график перехода в координатах р, Т. Поставим точку, соответствующую состоянию А газа (рис. 10.8, б). Процесс А—1 изотермический. При этом давление газа уменьшается. Процесс 1—2 изобарный. Построим отрезок, параллельный оси абсцисс. Процесс 2—В изохорный, при этом температура газа уменьшается. Начертим изохору, проходящую через точку 2. Конечное состояние соответствует давлению р_B.

Аналогично строим переход в координатах V, Т (рис. 10.8, в). При процессе А—1 объём газа увеличивается при постоянной начальной температуре. При процессе 1—2 объём увеличивается при постоянном давлении. Изобара проходит через начало координат. Конечное состояние соответствует объёму V_B. Затем процесс изохорный, при этом температура газа понижается.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основные положения МКТ. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика

Почему тепловые явления изучаются в молекулярной физике —
Основные положения молекулярно-кинетической теории. Размеры молекул —
Примеры решения задач по теме «Основные положения МКТ» —
Броуновское движение —
Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел —
Идеальный газ в МКТ. Среднее значение квадрата скорости молекул —
Основное уравнение молекулярно-кинетической теории газов —
Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» —
Температура и тепловое равновесие —
Определение температуры. Энергия теплового движения молекул —
Абсолютная температура. Температура — мера средней кинетической энергии молекул —
Измерение скоростей молекул газа —
Примеры решения задач по теме «Энергия теплового движения молекул» —
Уравнение состояния идеального газа —
Примеры решения задач по теме «Уравнение состояния идеального газа» —
Газовые законы —
Примеры решения задач по теме «Газовые законы» —
Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»

Источник

Изопроцессы в МКТ — это процессы, протекающие в газах с каким-нибудь неизменным параметром. Рассмотрим, как решаются некоторые задачи, представленные в графиках, при наличии неизменных параметров.

Задача 1: Постоянная масса идеального газа участвует в процессе, указанном на рисунке. Где давление газа будет наибольшим?

Приступаем. Фраза «постоянная масса газа» означает, что мы имеем задачу с изопроцессом. Смотрим.

1-2: Температура не меняется (изотерма), но при этом увеличивается объем. В изотермическом процессе увеличение объема ведет к уменьшению давления и наоборот. Давление обратно пропорционально объему. Следовательно, в точке 2 давление ниже, чем в точке.

2-3: Не меняется объем (изохора), но при этом температура уменьшается. А в изохорном процессе давление прямо пропорционально температуре. То есть, в нашем случае — уменьшается.Давление в точке 3 будет меньше, чем в точке 2.

Ответ: Наибольшее давление будет в точке 1.

Задача 2: Зависимость объема идеального газа от температуры показана на V-P диаграмме. Масса газа постоянна. Выберите два верных утверждения о процессе, происходящем с газом:

Давление газа максимально в состоянии D.
При переходе из состояния D в состояние А средняя квадратичная скорость молекул увеличивается.
При переходе из состояния В в состояние С плотность газа возрастает.
Давление газа в состоянии С больше, чем в состоянии А
При переходе из состояния В в состояние С средняя кинетическая энергия молекул возрастает

Процесс, изображенный на диаграмме (окружность), конечно же не является изопроцессом в чистом виде. Но у нас есть газ постоянной массы, а следовательно, мы можем воспользоваться графиками изобар для сравнения давления в заданных точках диаграммы. Температуру и объем можно сравнить на диаграмме по осям. Изобары здесь уже нарисованы. Это красная, синяя и коричневая прямые, то есть в этих осях на каждой изохоре какое-то свое, но постоянное даление. Для сравнения давления в точках можно провести изотерму или изохору. Я провела изохору. Смотрим. При постоянном объеме температура газа увеличивается от точки 1 до точки 3. Соответственно наибольшее давление на коричневой изобаре, а наименьшее — на красной. В точках А и С давление одинаковое, т.к. они лежат на изобаре.

Максимальное давление соответствует точке D. Первое утверждение верно.

При рассмотрении уравнения состояния идеального газа было определено, что давление прямо пропорционально температуре и средней квадратичной скорости движения молекул

р ∼ Т ∼ v²

Максимальная скорость соответствует максимальному давлению, значит в точке А она , скорость, меньше, чем в точке В. Второе утверждение неверно

Теперь плотность. Плотность — это масса единицы объема. Масса у нас постоянная, а объем в точке С больше, чем в точке В. Значит, плотность будет меньше. Третье утверждение неверно.

В точках А и С давление одинаковое, т.к. они лежат на изобаре. Четвертое утверждение неверное.

При переходе из В в С давление увеличивается, следовательно, увеличивается средняя квадратичная скорость, а значит, увеличивается средняя кинетическая энергия. Пятое утверждение верное.

Ответ: 1 и 5

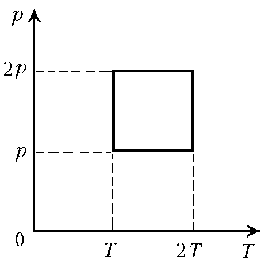
Задача 3: В сосуде находится идеальный газ, массу которого изменяют. На диаграмме показан процесс изохорного изменения состояния газа. В какой точке диаграммы масса газа наибольшая?