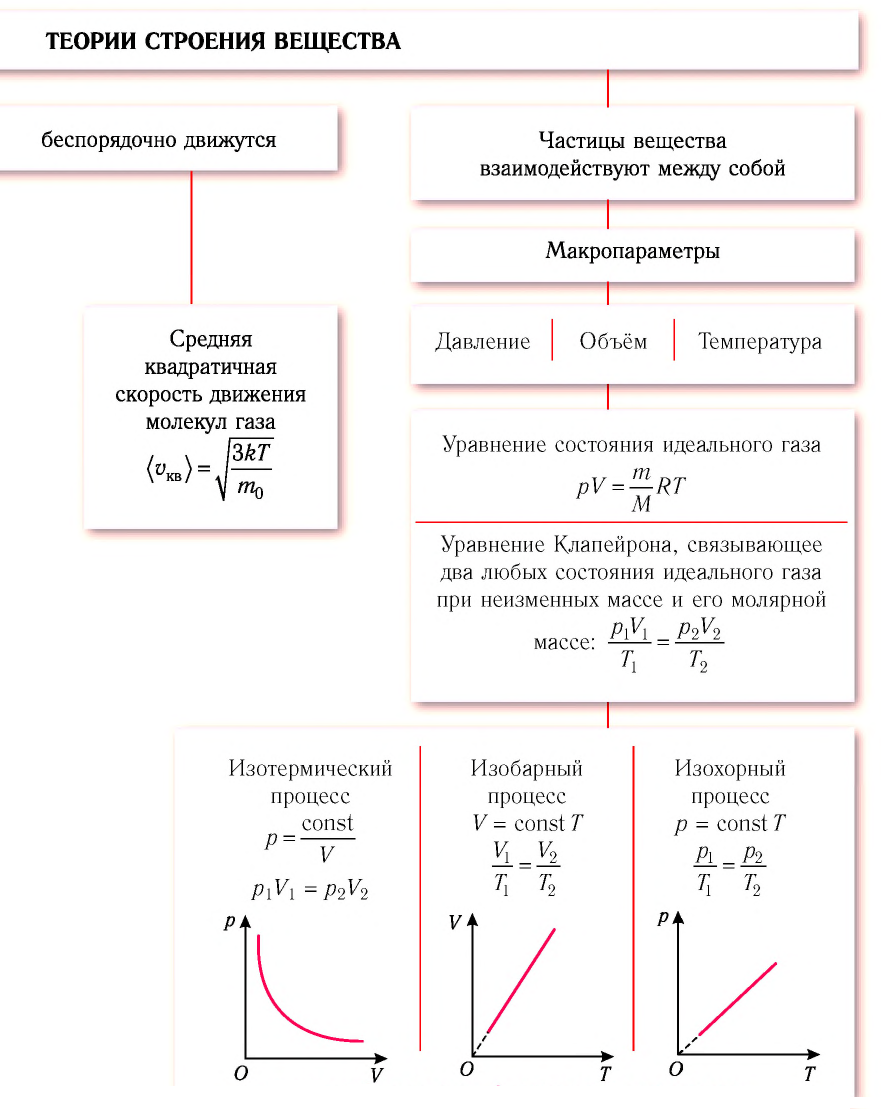
Изопроцессы
-
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
-
Изотермический процесс
-
Графики изотермического процесса
-
Изобарный процесс
-
Графики изобарного процесса
-
Изохорный процесс
-
Графики изохорного процесса
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• 
, то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• 
, то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: 
.
2. Изобарный процесс идёт при постоянном давлении газа: 
.
3. Изохорный процесс идёт при постоянном объёме газа: 
.
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
к оглавлению ▴
Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре 
. В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны 
, а во втором — 
. Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса 
и молярная масса 
предполагаются неизменными.
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
(1)
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
(2)
Данное утверждение называется законом Бойля — Мариотта.
Записав закон Бойля — Мариотта в виде
(3)
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
к оглавлению ▴
Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
• 
-диаграмма: ось абсцисс 
, ось ординат 
;
• 
-диаграмма: ось абсцисс , ось ординат ;
• 
-диаграмма: ось абсцисс , ось ординат .
График изотермического процесса называется изотермой.
Изотерма на -диаграмме — это график обратно пропорциональной зависимости 
.
Такой график является гиперболой (вспомните алгебру — график функции 
). Изотерма-гипербола изображена на рис. 1.
Рис. 1. Изотерма на -диаграмме
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на –диаграмме.
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2). Первый процесс идёт при температуре 
, второй — при температуре 
.
Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление 
, на второй — 
. Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, 
.
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):
Рис. 3. Изотермы на и -диаграммах
к оглавлению ▴
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня 
и поперечное сечение поршня 
, то давление газа всё время постоянно и равно
где 
— атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны 
и 
.
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
(4)
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
(5)
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:
(6)
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
к оглавлению ▴
Графики изобарного процесса
График изобарного процесса называется изобарой. На -диаграмме изобара 
является прямой линией (рис. 4):
Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на –диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и 
(рис. 5):
Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что 
. Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):
Рис. 6. Изобары на и -диаграммах
к оглавлению ▴
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами 
и 
. Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
(7)
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
(8)
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:
(9)
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
к оглавлению ▴
Графики изохорного процесса
График изохорного процесса называется изохорой. На -диаграмме изохора 
является прямой линией (рис. 7):
Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Далее, чем больше объём, тем ниже идёт изохора на –диаграмме (рис. 8):
Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что 
. Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, 
.
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):
Рис. 9. Изохоры на и -диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Изопроцессы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Содержание:
Изотермический, изобарный и изохорный процессы:
Свойство газов существенно изменять предоставленный им объём широко используют в тепловых двигателях. Анализируя процессы, происходящие с газом в этих устройствах, важно знать, каким законам подчиняются газы и каковы условия применимости этих законов.
Процессы в газах часто происходят так, что изменяются только два параметра из пяти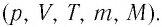 
Изотермический процесс
Процесс изменения состояния физической системы при постоянной температуре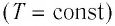 
называют изотермическим.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то из уравнения Клапейрона—Менделеева следует:
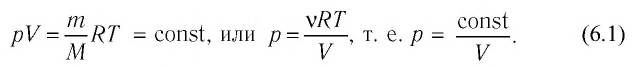
Давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму.
Это утверждение называют законом Бойля—Мариотта.
Справедливость закона Бойля—Мариотта можно продемонстрировать экспериментально, используя установку, представленную на рисунке 18 в § 5.
Если медленно изменять объём газа, находящегося в сосуде, то вследствие теплообмена с окружающей средой можно поддерживать температуру газа в сосуде практически постоянной. При этом уменьшение объёма газа при вращении винта 3 повлечёт за собой увеличение его давления и некоторое незначительное увеличение температуры. И наоборот, увеличение объёма приведёт к уменьшению давления и некоторому незначительному уменьшению температуры газа*.
* Незначительное изменение температуры газа принципиально необходимо для теплообмена с термостатом — передача тепла возможна только при разных температурах тел.
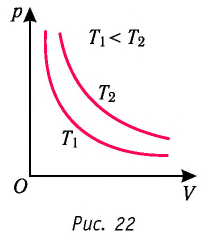
График изотермического процесса, совершаемого идеальным газом, в координатах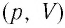 
представляет собой гиперболу (рис. 22). В физике такую кривую называют изотермой. Разным значениям температуры газа соответствуют разные изотермы. Согласно соотношениям (6.1) для одинаковых объёмов газов с одинаковыми количествами вещества и разными температурами чем больше давление, тем выше температура (рис. 22).
Многочисленные опыты показали, что исследованные газы подчиняются закону Бойля —Мариотта тем точнее, чем меньше их плотность. При значительном увеличении давления газа этот закон перестаёт выполняться.
Интересно знать:
Лёгкие расположены в грудной клетке, объём которой при дыхании периодически изменяется благодаря работе межрёберных мышц и диафрагмы. Когда грудная клетка расширяется, давление воздуха в лёгких становится меньше атмосферного, и воздух через воздухоносные пути устремляется в лёгкие — происходит вдох. При выдохе объём грудной клетки уменьшается, что вызывает уменьшение объёма лёгких. Давление воздуха в них становится выше атмосферного, и воздух из лёгких устремляется в окружающую среду.
Изобарный процесс
Процесс изменения состояния газа при постоянном давлении (р = const) называют изобарным.
В 1802 г. французский учёный Жозеф Гей-Люссак (1778-1850) рассмотрел этот процесс для воздуха, водорода, кислорода и азота.
Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона—Менделеева:
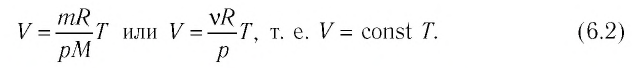
Объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре.
Это утверждение называют законом Гей-Люссака.
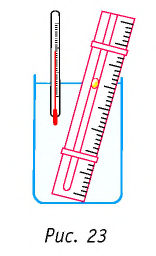
Справедливость закона Гей-Люссака можно продемонстрировать экспериментально, используя установку, представленную на рисунке 23. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым капелькой масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под капелькой масла, возрастает и капелька движется вверх. При уменьшении температуры объём воздуха уменьшается — и капелька движется вниз.
Поскольку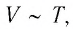 
то в координатах 
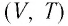график изобарного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 24). Эту линию называют изобарой.
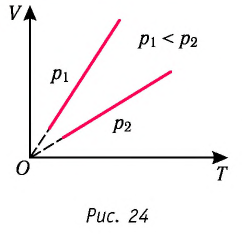
Изобара реальных газов не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы существенно отличаются от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости.
В одних и тех же координатах 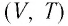можно построить несколько изобар, которые соответствуют разным давлениям данной массы идеального газа при неизменной молярной массе. Анализ соотношений (6.2) позволяет сделать вывод, что большему давлению соответствует меньший наклон изобары к оси температур (см. рис. 24).
Изохорный процесс
Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным.
Впервые этот процесс рассмотрел в 1787 г. французский учёный Жак Шарль (1746-1823)*.
* Несмотря на то что Шарль не опубликовал результаты своих исследований, история физики отдаёт приоритет открытия ему.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то давление газа, как следует из уравнения Клапейрона—Менделеева:
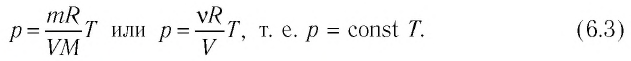
Давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре.
Это утверждение называют законом Шарля.
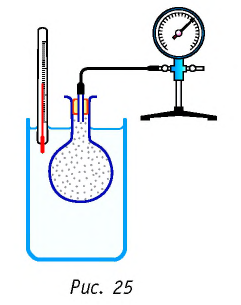
Справедливость закона Шарля можно продемонстрировать экспериментально, используя установку, представленную на рисунке 25. Колба, наполненная воздухом и соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры — давление воздуха уменьшается.
В координатах 
график изохорного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 26). Эту линию называют изохорой.
Как и в случае изобарного процесса, изохора реальных газов не может быть продлена до нулевого значения температуры.
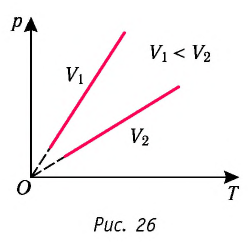
В одних и тех же координатах 
можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной моляр- О ной массе. Анализ соотношений (6.3) показывает, что большему объёму соответствует меньший наклон изохоры к оси температур (см. рис. 26).
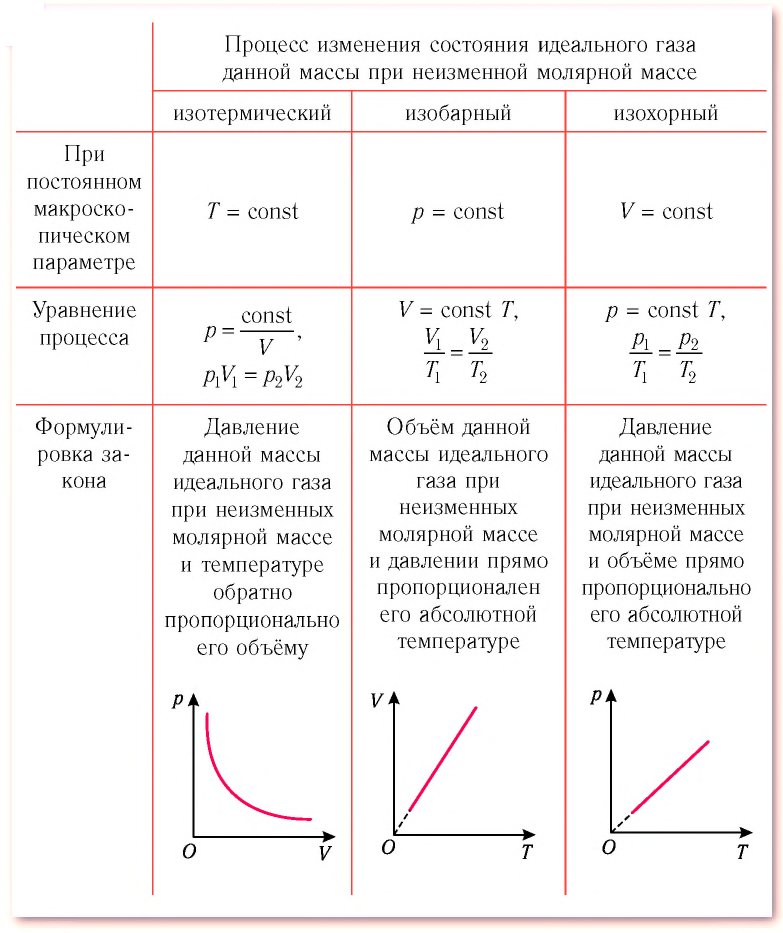
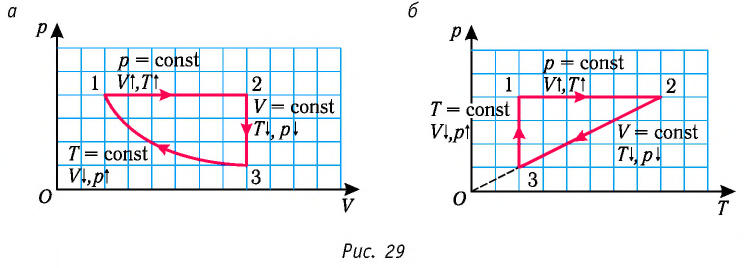
Пример №1
На рисунке 28 представлен график трёх процессов изменения состояния некоторой массы идеального газа. Как изменялись параметры газа на участках 
Изобразите эти процессы в координатах 
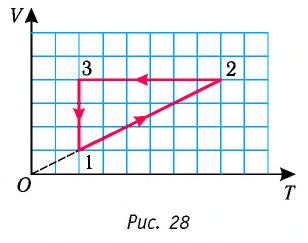
Решение. На участке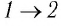 
объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:
переход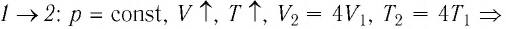 
происходит изобарное нагревание газа.
В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:
переход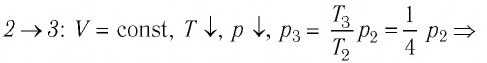 
происходит изохорное охлаждение газа.
Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля—Мариотта, увеличение давления газа в 4 раза:
- переход
происходит изотермическое сжатие газа.
происходит изотермическое сжатие газа.Опираясь на сделанные выводы, представим все три процесса в координатах 
(рис. 29, а, б).
Пример №2
При изотермическом расширении идеального газа определённой массы его объём увеличился от 
а давление уменьшилось на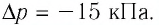 
Определите первоначальное давление газа.
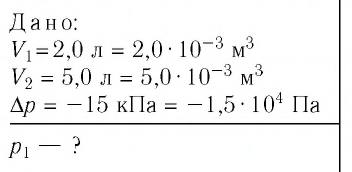
Решение. Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля—Мариотта, т. е.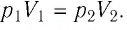 
С учётом того, что 
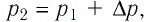получим:
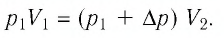
Откуда
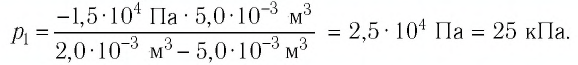
Ответ: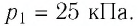 
Обобщение и систематизация определений:
- Твердые тела и их свойства в физике
- Строение и свойства жидкостей в физике
- Испарение и конденсация в физике
- Влажность воздуха в физике
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
Законы идеальных газов. Изопроцессы
Здесь рассматривается модель идеального газа, типичные процессы, которые с ней производятся: изотермический, изобарный, изохорный.
В статье рассматривается модель идеального газа и типичные процессы, которые с ней производятся: изотермический, изобарный, изохорный. Основную часть статьи представляют собой задачи с решениями, а в конце есть домашние задания.
Введение
В первую очередь хочется поговорить про идеальный газ. Что же он из себя представляет и почему он идеален?
Идеальный газ — теоретическая математическая модель газа, в которой пренебрегают размерами частиц и не учитывают силы взаимодействия между ними, предполагая, что их средняя кинетическая энергия много больше энергии их взаимодействия. Считается, что столкновения частиц газа между собой и со стенками сосуда абсолютно упругие.
Существует модель классического идеального газа, свойства которого описываются законами классической физики, и модель квантового идеального газа, подчиняющегося законам квантовой механики. Обе модели идеального газа справедливы для реальных классических и квантовых газов при достаточно высоких температурах и разряжениях.
В реальных же газах при некоторых расчетах мы не можем пренебрегать вышеуказанными приближениями. Например, вы можете столкнуться с газом Ван-дер-Ваальса, в уравнении которого есть поправка на объем и давление.
Какими величинами можно охарактеризовать состояние идеального газа?
Считая, что нам известен химический состав газа и его масса, для описания его состояния мы можем воспользоваться такими параметрами, как объем V, занимаемый газом, давление Р, температура Т. Связь между этими параметрами идеальных газов отражают четыре основных закона: закон Бойля — Мариотта, закон Гей-Люссака, закон Шарля и закон Клапейрона — Менделеева. Пользуясь уравнениями, описывающими эти законы, можно решать практически любые задачи, в которых нас интересует физическое состояние идеального газа.
Среди различных газовых процессов можно выделить такие, в которых одна из величин (T, P или V) поддерживается постоянной.
Изотерма
Изотермическими называются процессы, в которых температура постоянна: Т = const. Такие процессы, описывает закон Бойля — Мариотта:
P₁V₁ = P₂V₂,
где индексы 1 и 2 относятся к начальному и конечному состояниям газа.
Одним из основополагающих знаний про изопроцессы, в частности, для понимания темы и для решения задач, является вид графиков этих процессов в разных координатах.
Задача. Посредине узкой, запаянной с обоих концов горизонтальной трубки (рис. 2) находится столбик ртути длиной h = 25 см. Ртуть разделяет в трубке два столба воздуха длиной l₀ = 1 м каждый. Давление воздуха 76 см. рт. ст., температура остается постоянной. На какое расстояние х переместится столбик ртути, если трубку поставить вертикально?
Решение. Рассмотрим отдельно два столбика воздуха в стоящей вертикально трубке и применим закон Бойля — Мариотта к каждому из них (площадь сечения трубки S):
(1) P₀l₀S = P₁(l₀ + x)S,
(2) P₀l₀S = P₁(l₀ – x)S.
Из условия механического равновесия столбика ртути следует, что при вертикальном положении трубки давление в нижнем столбе воздуха равно
P₂ = P₁ + ρgh,
(ρ — плотность ртути). Подставив это значение P₂ в (2), получим квадратное уравнение, решив которое, найдем, что
(Отрицательное значение корня не имеет смысла).
Интересно отметить, что при вычислении неизвестного х нам не нужны сведения о плотности ртути ρ, а также о соотношениях между единицами давления. Дело в том, что по определению давление Р, которое создает 1 см. рт. ст., равно P = ρg · 1 см. Следовательно, P / ρg = 76 см без каких-либо дополнительных пересчетов.
Изобара
В изобарных процессах постоянно давление (P = const). Закон, описывающий этот процесс, называется законом Гей-Люсакка:
V₁ / T₁ = V₂ / T₂.
Графики при изобарном процессе:
Изохора
При изохорном процессах постоянным поддерживается объем газа (V = const), и закон, описывающий этот процесс, носит название закона Шарля:
P₁ / T₁ = P₂ / T₂.
Примеры
Рассмотрим теперь одну графическую задачу.
Задача. С идеальным газом происходит циклический процесс, график которого в координатах «давление-объем» приведен на рисунке (участок графика 2–3 — изотерма). Построить графики зависимости P(T) и V(T) для этого процесса.
Решение. Исследуем отдельно все участки процесса: 1–2, 2–3 и 3–1. Как видно из данного в условии графика, процесс 1–2 является изохорическим с ростом давления.
Поэтому на графиках P(T) и V(T) ему отвечают прямая, продолжение которой проходит через начало координат, и горизонтальная прямая соответственно, причем и давление, и температура в этом процессе растут (участки 1–2).
Процесс 2–3 является изотермическим (это говорится в условии) с ростом объема газа и убыванием давления. Поэтому на графиках P(T) и V(T) ему отвечают вертикальные прямые: убывающая на графике P(T) и растущая на графике V(T) (участки 2–3). Как следует из рисунка, процесс 3–1 является изобарическим, в нем объем газа убывает. Поэтому ему отвечают горизонтальная прямая на графике P(T) и прямая, продолжение которой проходит через начало координат, на графике V(T). Поскольку, совершив процесс 1–2–3–1, газ возвращается в первоначальное состояние, все графики должны быть замкнуты. Это значит, что соответствующие прямые должны попасть в начальную точку 1 (участки 3–1).
Рассмотрим еще несколько задач.
Задача. Определить температуру газа, находящегося в закрытом сосуде, если при нагревании газа на ΔT = 1 °С давление газа увеличивается на величину, составляющую α часть от первоначального давления (α = 0,004).
Решение. Так как объем сосуда в рассматриваемом процессе не меняется, то давление и температура газа в нем связаны законом Шарля. Из этого закона для начального и конечного состояния газа имеем:
Решая это уравнение, находим:
Задача. Во фляжке вместимостью 0,5 л находится 0,3 л воды. Турист пьет из неё воду, плотно прижав губы к горлышку так, что во фляжку не попадает наружный воздух. Сколько воды удастся выпить туристу, если он может понизить давление оставшегося во фляжке воздуха до 80 кПа.
Решение. Согласно условию задачи, исходный объем воздуха во фляжке V₁ = 0,2 л, а исходное давление равно атмосферному P₁ = 100 кПа. Если считать процесс поглощения воды туристам изотермическим, то, конечно, объем воздуха можно найти из закона Бойля-Мариотта:
Таким образом, объем воздуха во фляжке увеличится на 0,05 л = 50 см³ — именно такой объем воды и сможет выпить турист.
Из сказанного ясно, что параметры, определяющие состояние данной массы газа, неизменного химического состава (Р, V и Т) и связаны друг с другом. Если известны две величины, можно найти третью.
Уравнение, определяющее связь температуры, объема и давления, называют уравнением состояния газа, или, в честь открывших его ученых, уравнением Менделеева-Клапейрона. Подробнее о нем мы расскажем в следующей статье.
Задачи для самостоятельного решения
Задачи разделены на 3 уровня Л — легкий, С — средний, П — повышенный.
Задача 1. (Л). При увеличении давления в 1.5 раза объем газа уменьшился на 30 мл. Найти первоначальный объем газа. (90 мл)
Задача 2. (Л). Какой объем займет газ при температуре 77 ℃, если при температуре 27 ℃ его объем был 6л? (7 л)
Задача 3. (C). С идеальным газом происходит процесс, график которого в координатах «давление-объем» приведен на рисунке. Определить отношение максимальной и минимальной абсолютных температур газа в течение всего процесса. Все необходимые величины приведены на рисунке, k и n — известные числа. (T₃ / T₁ = nk)
Задача 4. (C). Построить эквивалентные графики в P(T) и V(T) координатах.
Задача 5. (П). Водяной паук Серебрянка строит в воде воздушный домик, перенося на лапках и брюшке пузырьки атмосферного воздуха и помещая их под купол паутины, прикрепленный концами к водяным растениям. Сколько рейсов надо сделать пауку, чтобы на глубине 50 см построить домик объемом 1 см³, если каждый раз он берет 5 мм³ воздуха под атмосферным давлением? (N = 210 раз)
А.Ю. Рудь
Список литературы
- Буховцев Б. Законы идеальных газов // Квант. №5. Квант. М., 1972.
- Гельфгат И.М. 1001 задача по физике с решениями. М., 1998.
- Савельев И.В. Курс общей физики. Т.1. Механика, колебания и волны, молекулярная физика. М., 1970.
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
Какой процесс называется изохорным, условия протекания
Определение
Изохорным процессом называют термодинамический процесс, протекающий при условии постоянного объема.
Изохорный процесс можно наблюдать опытным путем. Для этого необходимо повышать или понижать температуру вещества в газообразном или жидком состоянии, находящегося в сосуде и сохраняющего стабильность объема. В случае, когда манипуляции производят с идеальным газом, его давление и температура будут изменяться прямо пропорционально, согласно закону Шарля. Для реальных газов данная закономерность не применима.
История возникновения теории, кто открыл, формула
Изучение изохорного процесса связывают с Гийомом Амонтоном. Работа ученого под названием «Парижские мемуары», написанная в 1702 году, посвящена исследованию характеристик газообразного вещества, помещенного в фиксированный объем, который составляет часть «воздушного термометра». Равновесие жидкости в данных условиях объясняется воздействием на нее давления газа, находящегося в сосуде, и атмосферного давления. Если температура среды повышается, показатели давления в резервуаре возрастают. При этом определенный объем жидкости вытесняется в выступающую трубку. Зависимость между такими характеристиками процесса, как температура и давление, представлена на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В 1801 году были опубликованы два эссе исследователя Джона Дальтона с описанием эксперимента, результаты которого демонстрируют одинаковое расширение всех газов и паров при постоянном давлении и изменении температуры, когда начальная и конечная температура одинакова. В итоге был сформулирован закон Гей-Люссака. Ученый, в честь которого явление получило название, экспериментальным путем подтвердил одинаковое расширение различных газообразных веществ и вывел коэффициент, практически равный коэффициенту, полученному Дальтоном. Благодаря объединению данной закономерности с законом Бойля-Мариотта, был описан изохорный процесс.
График изохорного процесса в идеальном газе
Зависимость характеристик при изохорном процессе можно представить схематично. График на диаграмме в системе координат будет иметь следующий вид:
В случае идеального газа графически изохорные процессы будут изображены следующим образом:
Первый закон термодинамики для изохорного процесса
В условиях термодинамического процесса формула элементарной работы имеет следующий вид:
(delta A=PdV)
Преобразование данного выражения позволит рассчитать величину полной работы процесса:
(A=int_{V_{1}}^{V_{1}}{PdV})
В случае, когда объем сохраняет стабильность, то есть (dV=0), значение интеграла будет нулевым. Исходя из этого, в изохорном процессе работа газа не наблюдается:
(A=0)
Изменение внутренней энергии для идеального газа рассчитывается по формуле:
(Delta U=frac{i}{2}nu RDelta T)
где i представляет собой количество степеней свободы, зависящее от числа атомов, которыми обладает молекула газа. В качестве примера можно рассмотреть такие вещества:
- одноатомная молекула неона обладает тремя степенями;
- пять степеней характерно для двухатомной молекулы кислорода;
- в молекуле с тремя и более атомами, как у водяного пара, насчитывается 6 степеней.
Формула внутренней энергии выходит из понятия и уравнения теплоемкости, представляет собой следующее отношение:
(Delta U=nu c_{upsilon }^{mu }Delta T)
где (c_{upsilon }^{mu }) является молярной теплоемкостью в условиях постоянного объема.
Расчет количества теплоты выполняют с помощью первого начала термодинамики в условиях термодинамического процесса:
(Q=Delta U+A)
Следует учитывать, что в условиях изохорного процесса газообразное вещество не выполняет работу. Исходя из этого, можно вывести формулу:
(Q=Delta U=nu c_{upsilon }^{mu }Delta T)
Согласно уравнению, газ получает теплоту. Она полностью расходуется, чтобы изменять внутреннюю энергию газообразного вещества.
Изменения термодинамических параметров в изохорном процессе
В условиях изохорного процесса наблюдается теплообмен с внешней средой. Данное явление называют изменением энтропии. Из его понятия следует уравнение:
(dS=frac{delta Q}{T})
где (delta Q) является элементарным количеством теплоты.
Преобразуя уравнение для расчета количества теплоты в дифференциальный вид, получают следующую формулу:
(delta Q=nu c^{mu }_{upsilon }dT)
где (nu) является количеством вещества, а (nu c^{mu }_{upsilon }) обозначает молярную теплоемкость в условиях постоянного объема.
Формула микроскопического изменения энтропии в условиях протекания изохорного процесса имеет вид:
(dS=frac{nu c^{mu }_{upsilon }dT}{T}dy/dx dy/dx)
Если проинтегрировать последнюю формулу, то расчет полного изменения энтропии выполняют таким образом:
(int_{S_{1}}^{S_{2}}{dS}=nu int_{T_{1}}^{T_{2}}frac{c^{mu }_{upsilon }dT}{T}Rightarrow Delta S=nu int_{T_{1}}^{T_{2}}frac{c^{mu }_{upsilon }dT}{T})
В этой ситуации не представляется возможным вынести определение молярной теплоемкости в условиях стабильного объема за интеграл, так как оно представлено в виде функции, зависящей от температуры.
Применение эффекта изохорного процесса
Идеальный цикл Отто приближенно воспроизведен в конструкции мотора внутреннего сгорания, работающего на бензине. Такты 2-3 и 4-1 при его функционировании представляют собой изохорные процессы. На выходе двигателя совершается работа. Она рассчитывается, как разность работ. К одной из них относят работу, производимую газообразным веществом над поршнем в процессе третьего такта или рабочего хода, к другой – работу, затраченную поршнем во время сжатия газа при втором такте. Таким образом, на примере двигателя, функционирующего, согласно принципу Отто, в системе принудительного сжигания смеси, газообразное вещество сжимается до 7-12 раз.
На рисунке изображен классический двигатель Стирлинга с конструкцией бета-типа, для которой характерно расположение рабочего и вытеснительного поршня в одном цилиндре.
Динамику цикла Отто можно представить в следующем виде:
Цикл Стирлинга также характеризуется наличием двух изохорных тактов. Процесс протекает при дооснащении конструкции двигателя Стирлинга регенератором. Во время прохождения газообразного вещества в одном направлении через наполнитель осуществляется передача тепла от рабочего тела к регенератору. Если газ проходит в обратную сторону, то тепловая энергия передается на рабочее тело. Идеальный цикл Стирлинга достигает обратимости и характеризуется теми же параметрами КПД, что и цикл Карно.
