Молекулярная физика Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества

m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа

p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;
 — среднее значение квадрата скорости молекул.
— среднее значение квадрата скорости молекул.
1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта

p — давление;
V — объем газа.
1.7 Закон Шарля
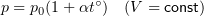
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака

V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа

ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV

p — давление газа.
При изменении объема от V1 до V2

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
Формулы молекулярной физики
Формула концентрации молекул
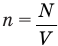
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
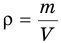
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
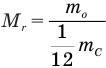
Здесь 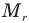 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 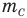 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
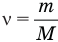
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
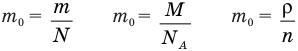
Здесь 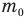 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 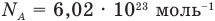 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
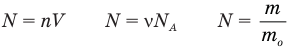
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 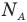 — число Авогадро
— число Авогадро 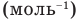 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
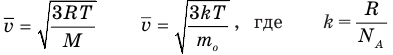
Здесь 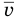 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 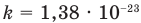 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 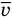 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
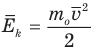
Здесь 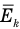 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 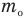 — масса одной молекулы (кг),
— масса одной молекулы (кг), 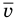 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
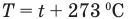
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
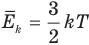
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
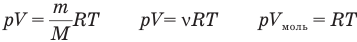
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 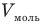 — объем моля
— объем моля 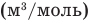 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 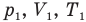 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 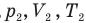 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 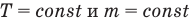
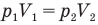
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 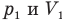 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 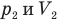 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 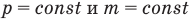
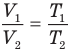
Здесь р — давление газа (Па), m — масса газа (кг), 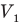 и
и 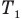 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 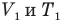 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 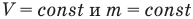
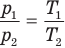
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 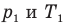 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 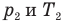 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
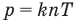
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
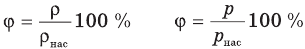
Здесь 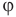 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 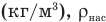 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 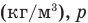 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 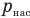 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
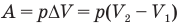
Здесь А — работа (Дж), р — давление газа (Па), 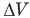 — изменение объема газа
— изменение объема газа 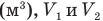 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
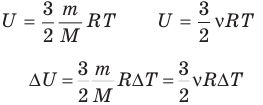
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 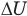 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 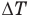 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
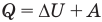
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 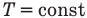
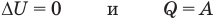
к изохорному: при V = const
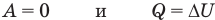
к изобарному: при р = const
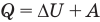
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем  , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
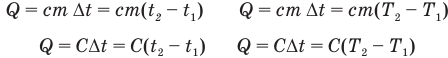
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 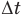 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 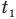 и
и 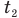 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 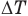 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 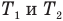 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 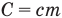 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
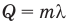
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 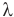 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
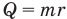
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
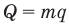
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
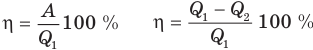
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 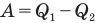 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 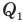 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 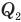 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
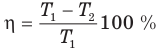
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 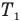 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 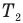 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

Как вычислить объем газа
Газ, как и вещества, находящиеся в других агрегатных состояниях, имеет ряд параметров, в число которых входит и объем. Объем газа находится на основании других его характеристик, которые приведены в условии задачи. Любой газ, независимо от вида и состава, имеет объем, который и требуется найти во многих задачах.
Инструкция
Газ, независимо от его состава, имеет три основных параметра: массу, объем и плотность. В большинстве задач оперируют так называемым идеальным газом, поэтому опираться в них необходимо лишь на приведенные в условии значения массы, давления, температуры. Например, в условии задачи может быть указан газ азот N2 с температурой в 60 градусов, давлением в 30 кПа и массой в 0,05 г. Зная эти три параметра и состав газа, по уравнению Менделеева-Клапейрона можно найти его объем. Для этого необходимо переделать данное уравнение следующим образом:
pV=mRT/M.
Осуществив дальнейшее преобразование формулы, найдите объем азота:
V =mRT/pM.
При этом молярную массу M можно найти по таблице Д.И. Менделеева. У азота она равна 12 г/моль. Тогда:
V=0,05*12*8,31*333/30*12≈4,61.
Если известны объем при нормальных условиях, а объем при других условиях является искомым, примените законы Бойля-Мариотта и Гей-Люссака:
pV/T=pнVн/Tн.
В таком случае преобразуйте формулу следующим образом:
pV*Tн=pнVн*T.
Отсюда объем V равен:
V=pнVн*T/p*Tн.
Индекс н означает величину того или иного параметра при нормальных условиях.
Если рассматривать объем газа с точки зрения термодинамики, можно заметить, что на газы могут действовать силы, за счет которых меняется объем. При этом давление газа постоянно, что характерно для изобарных процессов. В ходе таких процессов объем изменяется с одной величины на другую. Их можно обозначить как V1 и V2. В условиях ряда задач описывается некоторый газ, находящийся под поршнем в сосуде. При расширении этого газа поршень передвигается на некоторое расстояние dl, в результате чего осуществляется работа:
A=pdV=p(V2 -V1).
Эта формула связывает изменение объема газа и работу. Как известно, если дан конечный объем V2, то можно найти начальный объем V1:
V1=pV2-A/p.
Наконец, наиболее просто найти объем газа, исходя из двух других физических параметров – массы и плотности. Если в условиях задан газ с некоторой плотностью и массой, то его объем следует вычислять по формуле:
V=m/ρ.
У каждого газа имеется определенная плотность, как и у любого твердого или жидкого вещества. Поэтому, находя объем газа, в первую очередь необходимо учитывать именно этот параметр.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Молекулярная физика изучает свойства тел, руководствуясь поведением отдельных молекул. Все видимые процессы протекают на уровне взаимодействия мельчайших частиц, то, что мы видим невооруженным глазом — лишь следствие этих тонких глубинных связей….
Основные понятия
 Молекулярная физика иногда рассматривается как теоретическое дополнение термодинамики. Возникшая намного раньше, термодинамика занималась изучением перехода тепла в работу, преследуя чисто практические цели. Она не производила теоретического обоснования, описывая лишь результаты опытов. Основные понятия молекулярной физики возникли позже, в XIX веке.
Молекулярная физика иногда рассматривается как теоретическое дополнение термодинамики. Возникшая намного раньше, термодинамика занималась изучением перехода тепла в работу, преследуя чисто практические цели. Она не производила теоретического обоснования, описывая лишь результаты опытов. Основные понятия молекулярной физики возникли позже, в XIX веке.
Она изучает взаимодействие тел на молекулярном уровне, руководствуясь статистическим методом, который определяет закономерности в хаотических движениях минимальных частиц – молекул. Молекулярная физика и термодинамика дополняют друг друга, рассматривая процессы с разных точек зрения. При этом термодинамика не касается атомарных процессов, имея дело только с макроскопическими телами, а молекулярная физика, напротив, рассматривает любой процесс именно с точки зрения взаимодействия отдельных структурных единиц.
Все понятия и процессы имеют собственные обозначения и описываются специальными формулами, которые наиболее наглядно представляют взаимодействия и зависимости тех или иных параметров друг от друга. Процессы и явления пересекаются в своих проявлениях, разные формулы могут содержать одни и те же величины и быть выражены разными способами.
Количество вещества
Количество вещества определяет взаимосвязь между весом (массой) и количеством молекул, которые содержит эта масса. Дело в том, что разные вещества при одинаковой массе имеют разное число минимальных частиц. Процессы, проходящие на молекулярном уровне, могут быть поняты только при рассмотрении именно числа атомных единиц, участвующих во взаимодействиях. Единица измерения количества вещества, принятая в системе СИ, — моль.
Внимание! Один моль всегда содержит одинаковое количество минимальных частиц. Это число называется числом (или постоянной) Авогадро и равняется 6,02×1023.
Эта константа используется в случаях, когда для расчетов требуется учитывать микроскопическое строение данного вещества. Иметь дело с количеством молекул сложно, так как придется оперировать огромными числами, поэтому используется моль – число, определяющее количество частиц в единице массы.
Формула, определяющая количество вещества:

Расчет количества вещества производится в разных случаях, используется во многих формулах и является важным значением в молекулярной физике.
Давление газа
Давление газа — важная величина, имеющая не только теоретическое, но и практическое значение. Рассмотрим формулу давления газа, используемую в молекулярной физике, с пояснениями, необходимыми для лучшего понимания.
Для составления формулы придется сделать некоторые упрощения. Молекулы представляют собой сложные системы, имеющие многоступенчатое строение. Для простоты рассмотрим газовые частицы в определенном сосуде как упругие однородные шарики, не взаимодействующие друг с другом (идеальный газ).
Скорость движения минимальных частиц также будем считать одинаковой. Введя такие упрощения, не сильно меняющие истинное положение, можно вывести такое определение: давление газа — это сила, которую оказывают удары молекул газа на стенки сосудов.
При этом, учитывая трехмерность пространства и наличие двух направлений каждого измерения, можно ограничить количество структурных единиц, воздействующих на стенки, как 1/6 часть.
Таким образом, сведя воедино все эти условия и допущения, можем вывести формулу давления газа в идеальных условиях.
Формула выглядит так:
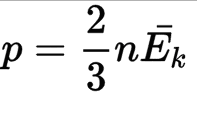
где P — давление газа,
n — концентрация молекул,
K — постоянная Больцмана (1,38×10-23),
Ek — кинетическая энергия молекул газа.
Существует еще один вариант формулы:
P = nkT,
где n — концентрация молекул,
T — абсолютная температура.
Формула объема газа
Объем газа — это пространство, которое занимает данное количество газа в определенных условиях. В отличие от твердых тел, имеющих постоянный объем, практически не зависящий от окружающих условий, газ может менять объем в зависимости от давления или температуры.
Формула объема газа – это уравнение Менделеева-Клапейрона, которое выглядит таким образом:
PV = nRT
где P — давление газа,
V — объем газа,
n — число молей газа,
R — универсальная газовая постоянная,
T — температура газа.
Путем простейших перестановок получаем формулу объема газа:
![]()
Важно! Согласно закону Авогадро равные объемы любых газов, помещенные в совершенно одинаковые условия — давление, температура — будут всегда содержать равное количество минимальных частиц.
Кристаллизация
Кристаллизация — это фазовый переход вещества из жидкого в твердое состояние, т.е. процесс, обратный плавлению. Процесс кристаллизации происходит с выделением теплоты, которую требуется отводить от вещества. Температура совпадает с точкой плавления, весь процесс описывается формулой:
Q = λm,
где Q — количество теплоты,
λ — теплота плавления,
M — масса.
Эта формула описывает как кристаллизацию, так и плавление, поскольку они, по сути, являются двумя сторонами одного процесса. Для того чтобы вещество кристаллизовалось, необходимо охладить его до температуры плавления, а затем отвести количество тепла, равное произведению массы на удельную теплоту плавления (λ). Во время кристаллизации температура не меняется.
Существует еще один вариант понимания этого термина — кристаллизация из перенасыщенных растворов. В этом случае причиной перехода становится не только достижение определенной температуры, но и степень насыщения раствора определенным веществом. На определенном этапе количество частиц растворенного вещества становится слишком большим, что вызывает образование мелких монокристалликов. Они присоединяют молекулы из раствора, производя послойный рост. В зависимости от условий роста кристаллы имеют различную форму.
Число молекул
Определить количество частиц, содержащееся в данной массе вещества, проще всего при помощи следующей формулы:
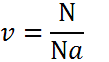
Отсюда выходит, что число молекул равняется:
![]()
То есть необходимо прежде всего определить количество вещества, приходящееся на определенную массу. Затем оно умножается на число Авогадро, в результате чего получаем количество структурных единиц. Для соединений подсчет ведется суммированием атомного веса компонентов. Рассмотрим простой пример:
Определим количество молекул воды в 3 граммах. Формула воды (H2O) содержит два атома водорода и один кислорода. Общий атомный вес минимальной частицы воды составит: 1+1+16 = 18 г/моль.
Количество вещества в 3 граммах воды:
3:18= 1/6.
Число молекул:
1/6 × 6 × 1023 = 1023.
Формула массы молекулы
Один моль всегда содержит одинаковое количество минимальных частиц. Следовательно, зная массу моля, можно разделить ее на количество молекул (число Авогадро), получив в результате массу системной единицы.
![]()
Следует учесть, что эта формула относится лишь к неорганическим молекулам. Размеры органических молекул намного больше, их величина или вес имеют совсем другие значения.
Молярная масса газа
Молярная масса — это масса в килограммах одного моля вещества. Поскольку в одном моле содержится одинаковое количество структурных единиц, формула молярной массы имеет такой вид:
M = κ × Mr
где k — коэффициент пропорциональности,
Mr — атомная масса вещества.
Молярная масса газа может быть рассчитана по уравнению Менделеева-Клапейрона:
pV = mRT / M,
из которой можно вывести:
M = mRT / pV
Таким образом, молярная масса газа прямо пропорциональна произведению массы газа на температуру и универсальную газовую постоянную и обратно пропорциональна произведению давления газа и его объема.
Внимание! Следует учесть, что молярная масса газа как элемента может отличаться от газа как вещества, например, молярная масса элемента кислорода (О) равна 16 г/моль, а масса кислорода как вещества (О2) равна 32 г/моль.
Основные положения МКТ.
Физика за 5 минут молекулярная физика
lt,span data-mce-type=bookmark style=display: inline-block, width: 0px, overflow: hidden, line-height: 0, class=mce_SELRES_startgt,lt,/spangt,
Вывод
Формулы, которые содержат молекулярная физика и термодинамика, позволяют вычислить количественные значения всех процессов, происходящих с твердыми веществами и газами. Такие расчеты необходимы как в теоретических изысканиях, так и на практике, поскольку они способствуют решению практических задач.
Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
,
где
Уравнение состояния идеального газа можно записать в виде:
,
где 


или в виде
,
где 


Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную 
Менделеев обнаружил, что 


Связь с другими законами состояния идеального газа[править | править код]
В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
— закон Бойля — Мариотта — Изотермический процесс.
— Закон Гей-Люссака — Изобарный процесс.
— закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс
В форме пропорции 
С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
.
- Закон Бойля — Мариотта
Закон Бойля — Мариотта
назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
где 

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение 

См. также[править | править код]
- Совершенный газ
- Реальный газ
- Уравнение состояния реального газа
Примечания[править | править код]
Литература[править | править код]
- Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.




