Урок 282
Тема урока: Задачи математической статистики.
Цели урока:
Обучающая:
Научить учащихся решать задачи по обработке
статистических данных, используя понятия:
объём измерения, размах измерения, мода
измерения, среднее арифметическое, медиана
измерения, варианта измерения, кратность
варианты, и составлять данные в виде таблиц,
диаграмм, графиков. Ввести понятия: частота
варианты, частота варианты (в процентах).
Развивающая:
Формировать умения
учащихся, решать задачи на
обработку статистических данных, используя
данные в виде таблиц, диаграмм, графиков.
Развивать логическое и математическое мышление.
Воспитывающая:
Воспитывать культуру речи,
построения плана
ответа, сознательной дисциплины, культуры
конструктивного мышления, активность на уроке,
аккуратность при выполнении записи на доске и в
тетради, положительный интерес к изучаемому
предмету.
Тип урока: Комбинированный.
Вид
урока: Урок
решения задач на обработку статистических
данных, используя данные в виде таблиц,
диаграмм, графиков.
Методы
обучения: Репродуктивный.
Материально-техническое
оснащение:
–Математика Учебник Общеобразовательные
дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва Издательский центр «Академия» 201
–Математика Учебник
Общеобразовательные дисциплины
для профессий и специальностей социально-экономического
профиля. Авторы В.А. Гусев, С.Г.Григорьев, С.В.Иволгина
Москва Издательский центр «Академия» 2011
– Математика Задачник Общеобразовательные
дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва
Издательский центр «Академия» 2012
– дидактический
раздаточный материал (карточки для
индивидуальной
работы)
Ход урока
1. Организационный момент урока
– сдача рапорта
2. Целевая ориентация
(
Преподаватель формулирует тему, цели и задачи урока. Мотивирует учащихся к
учебной деятельности. Разъясняет последовательность этапов урока, приводящих к
достижению цели)
3. Проверка
домашнего задания.
4. Вопросы для закрепления изученного
материала.
1). Перечислить
основные этапы простейшей статистической обработки данных.
2). Что называют
объемом измерения?
3). Что такое размах
измерения?
4). Что называют
модой измерения?
5). Что называют
средним арифметическим?
6). Что называют
вариантой измерения?
7). Что называют
медианой измерения?
5.
Формирование
навыков умственного труда
Решение задач у доски
Задача 1
В таблице распределения данных часть информации была утеряна.
Восстановить ее. Если известно, что объем измерения равен 20, размах измерения
равен 6, а мода равна 2.
|
|
Сумма |
|||||
|
– 1 |
0 |
3 |
||||
|
Кратность |
5 |
1 |
7 |
3 |
Решение
По определению. В графе «Сумма» должен стоять объём измерения, т.е. 20.
Этот объём равен сумме всех кратностей, значит, кратность варианты «0», равна
20 – (5+1+7+3) = 4.
Самая большая кратность равна 7. Значит, над ней и расположена мода
измерения, равная 2. Так как размах равен 6, а наибольшая варианта равна 3, то
наименьшая варианта равна 3 – 6 = – 3. эту варианту помещаем в последнюю
свободную графу над кратностью 5.
Ответ:
|
|
Сумма |
|||||
|
– 3 |
– 1 |
0 |
2 |
3 |
||
|
Кратность |
5 |
1 |
4 |
7 |
3 |
20 |
Задача 2
По приведённой гистограмме распределения данных найти: количество
вариант измерения, объем, размах. моду измерения, наиболее удалённую от моды
варианту и ее кратность. Составить таблицу распределения данных.
Решение.
Количество вариант – это количество столбиков в гистограмме, т.е. 7.
Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот
всех семи столбиков: 3+2+7+3+5+4+1 = 25. Таблица распределения выглядит так:
|
|
Сумма |
|||||||
|
2 |
4 |
5 |
6 |
7 |
9 |
10 |
||
|
Кратность |
3 |
2 |
7 |
3 |
5 |
4 |
1 |
25 |
1). Наибольшая варианта равна 10, а наименьшая равна 2.
2). Размах равен 8. (10 – 2) =8.
3). Мода измерения равна 5, так как она встречалась чаще других – 7
раз.
4). На наибольшем расстоянии от моды находится варианта 10, её
кратность равна 1.
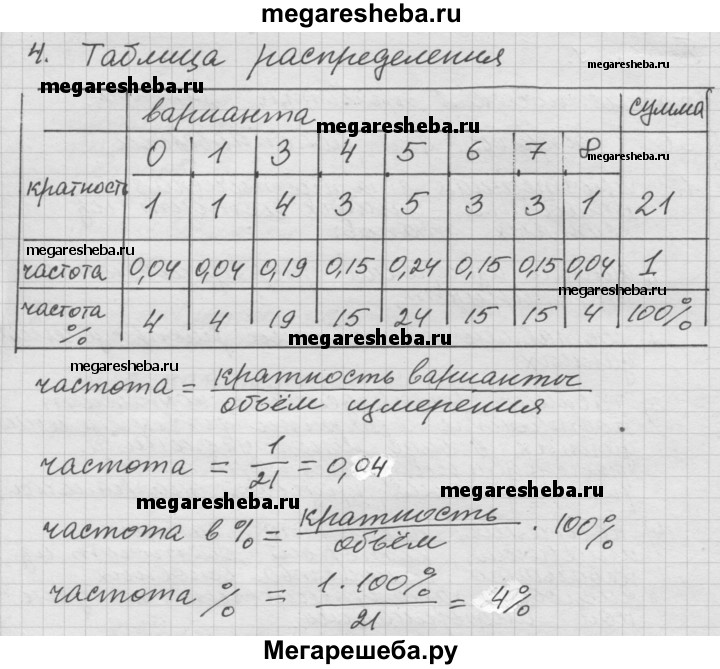
Определение: Если кратность варианты разделить на объем измерения,
то получится частота варианты. Это число показывает, какую
часть (долю) среди всех данных составляют данные, равные выбранной варианте.
Частоту варианты можно измерить и в процентах.
Частота варианты
(в процентах) =
Задача 3
В десятых классах трёх школ микрорайона провели проверочный диктант по
русскому языку. По их результатам изображена гистограмма распределения
полученных отметок.
а) Найти: общее
количество работ, частоту пятёрок, процентную частоту
двоек.
б) Заполнить сводную таблицу распределения данных.
в) Построить гистограмму распределения частот ( в процентах).
г) Построить круговую диаграмму распределения частот (в процентах).
Решение.
а) На гистограмме указано, что двоек было 40, троек – 50, четвёрок –
75, пятёрок – 35. значит. Всего было 200 работ. Это есть объём измерения.
Частота пятёрок равна , а частота (в процентах) двоек
равна
б) Так как все кратности известны, то можно заполнить всю таблицу
распределения:
|
|
Сумма |
||||
|
2 |
3 |
4 |
5 |
||
|
Кратность |
40 |
50 |
75 |
35 |
200 |
|
Частота |
0,2 |
0.25 |
0.375 |
0,175 |
1 |
|
Частота,% |
20 |
25 |
37,5 |
17,5 |
100 |
в) Для построения гистограммы распределения частот (в процентах)
используем первую и четвёртую строки. Получим четыре вертикальных столбика.
Основания которых соответствуют полученным отметкам, а высоты равны найденным
частотам ( в процентах).
г) разделим круг на четыре сектора. Центральный угол сектора двойки
составляет 20% от 3600. т.е. 720. Центральный угол
сектора тройки составляет 25% от 3600, это прямой угол. Центральные
углы секторов четвёрки и пятёрки равны соответственно 1350 и 630.

5. Вопросы для
закрепления изученного материала.
1). Что называют частотой
варианты?
2). По какой формуле
измеряют частоту варианты в процентах?
6. Итог урока.
Домашнее задание.
Задача.
По приведённой гистограмме распределения данных найти:
а) количество вариант и объем измерения;
б) размах и моду измерения;
в) таблицу распределения данных;
г) среднее результатов измерения.
Решение.
1) Количество вариант – это количество столбиков в гистограмме, т.е. 9.
Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот
всех девяти столбиков: 5+6+3+7+4+11+5+4+5 = 50. Таблица распределения выглядит
так:
|
|
Сумма |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
Кратность |
5 |
6 |
3 |
7 |
4 |
11 |
5 |
4 |
5 |
50 |
2). Наибольшая варианта равна 10, а наименьшая равна 2.
Размах равен 8. (10 – 2) = 8.
Мода измерения равна 7, так как она встречалась чаще других – 11 раз.
3). Таблица распределения выглядит так:
|
|
Сумма |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
Кратность |
5 |
6 |
3 |
7 |
4 |
11 |
5 |
4 |
5 |
50 |
4). Среднее арифметическое
– это частное от деления суммы всех результатов измерения на объём измерения.
Среднее удобно вычислять после того, как составлена таблица распределения. В
данном случае вычисления выглядят так:
Нормальное распределение: понимание гистограмм и вероятностей
Добавлено 14 августа 2020 в 19:41
В данной статье мы продолжаем исследование нормального распределения, рассматривая концепцию гистограмм и вводя функцию массы вероятности.
Данная статья является частью серии статей о статистике в электротехнике, которую мы начали с обсуждения статистического анализа и описательной статистики. Затем мы исследовали три описательных статистических показателя с точки зрения применения в обработке сигналов.
Затем мы коснулись стандартного отклонения (в частности, определения компенсации размера выборки при вычислении стандартного отклонения и понимания взаимосвязи между стандартным отклонением и среднеквадратичным значением).
В прошлой статье мы представили нормальное распределение в электротехнике, заложив основу для нашего текущего обсуждения: понимание вероятностей в измеренных данных.
Понимание гистограмм
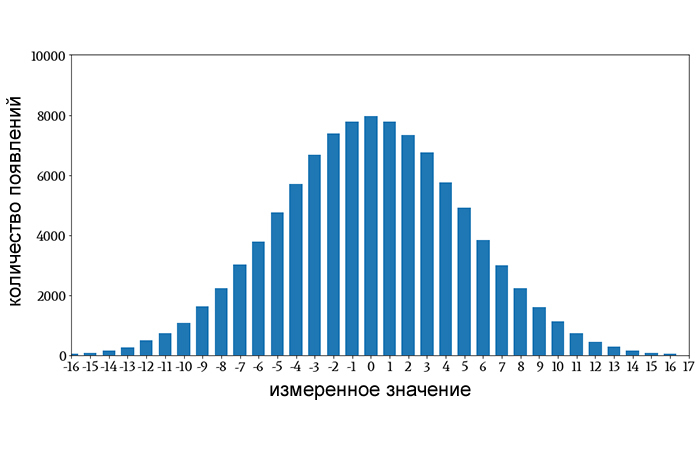
В предыдущей статье мы начали обсуждение нормального распределения, обратившись к форме этой гистограммы:
Я думаю, что большинство людей, работающих в области науки или техники, хотя бы смутно знакомы с гистограммами, но давайте сделаем шаг назад.
Что такое гистограмма?
Гистограммы – это визуальные представления 1) значений, присутствующих в наборе данных, и 2) частоты появления этих значений. Показанная выше гистограмма может представлять множество различных типов информации.
Представим, что она представляет собой распределение значений, полученных нами при измерении разницы, округленной до ближайшего милливольта, между номинальным и фактическим выходным напряжением линейного стабилизатора, который подвергался различным температурам и условиям эксплуатации. Так, например, примерно 8000 измерений показали разницу в 0 мВ между номинальным и фактическим выходными напряжениями, а примерно 1000 измерений показали разницу в 10 мВ.
Гистограммы – чрезвычайно эффективный способ обобщения больших объемов данных. Взглянув на гистограмму выше, мы можем быстро найти частоту отдельных значений в наборе данных и определить тенденции или закономерности, которые помогут нам понять взаимосвязь между измеренным значением и частотой.
Гистограммы с интервалами
Когда набор данных содержит так много разных значений, что мы не можем удобно связать их с отдельными столбцами гистограммы, мы используем объединение в интервалы (биннинг). То есть мы определяем диапазон значений как интервал, группируем результаты измерений в эти интервалы и создаем по одному столбцу для каждого интервала.
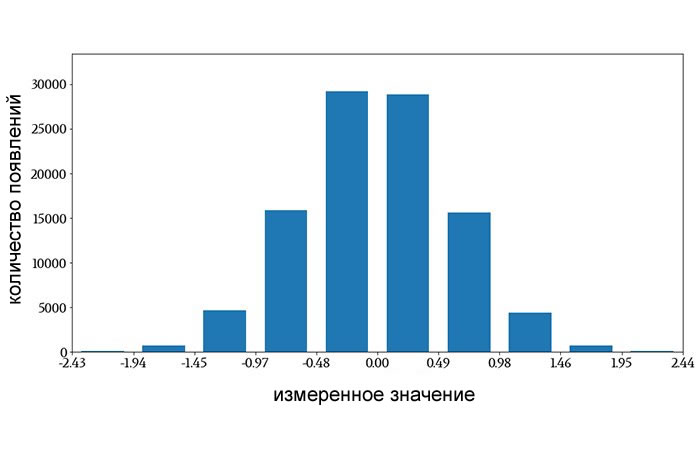
Следующая гистограмма, которая была сгенерирована из нормально распределенных данных со средним значением 0 и стандартным отклонением 0,6, использует интервалы вместо отдельных значений:
Горизонтальная ось разделена на десять интервалов одинаковой ширины, и каждому интервалу назначен один столбец. Все результаты измерений, попадающие в числовой интервал, влияют на высоту соответствующего столбца (метки на горизонтальной оси показывают, что интервалы не одинаковой ширины, но это просто потому, что значения меток округлены).
Гистограммы и вероятность
В некоторых ситуациях гистограмма не дает нужной нам информации. Мы можем посмотреть на гистограмму и легко определить частоту измеренного значения, но не можем легко определить вероятность измеренного значения.
Например, если я посмотрю на первую гистограмму, я знаю, что примерно 8000 измерений показали разницу в 0 В между номинальным и фактическим напряжениями стабилизатора, но я не знаю, какова вероятность того, что результат случайно выбранного измерения или нового измерения сообщит о разнице в 0 В.
Это серьезное ограничение, потому что вероятность отвечает на чрезвычайно распространенный вопрос: каковы шансы, что…?
Каковы шансы, что у моего линейного стабилизатора погрешность выходного напряжения будет менее 2 мВ? Какова вероятность того, что частота битовых ошибок моего канала передачи данных будет выше 10-3? Какова вероятность того, что из-за шума мой входной сигнал превысит порог срабатывания? И так далее.
Причина этого ограничения заключается в том, что гистограмма просто четко не передает размер выборки, то есть общее количество измерений (теоретически общее количество измерений можно определить, сложив значения всех столбцов гистограммы, но это было бы утомительно и неточно).
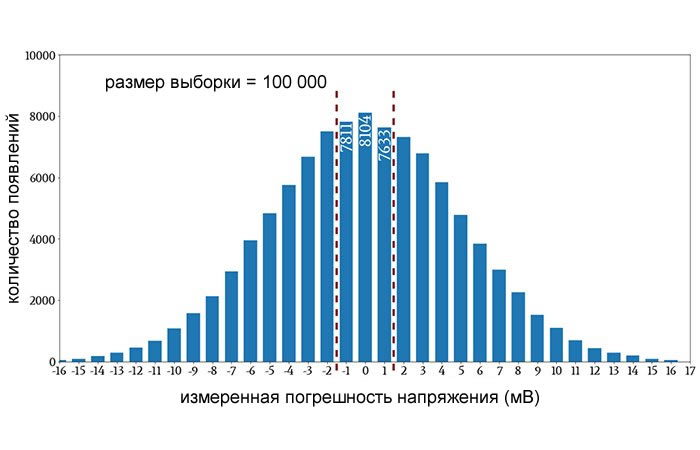
Если мы знаем размер выборки, мы можем разделить количество появлений на размер выборки и таким образом определить вероятность. Давайте рассмотрим пример.
Красные пунктирные линии заключают в себя столбцы, которые указывают на погрешности напряжения менее 2 мВ, а числа, написанные внутри столбцов, указывают точное количество появлений этих трех значений погрешности напряжения. Сумма этих трех чисел составляет 23 548. Таким образом, на основе этого примера по сбору данных вероятность получения погрешности менее 2 мВ составляет 23 548/100 000 ≈ 23,5%.
Функция массы вероятности
Если наша основная цель при создании гистограммы – передать информацию о вероятности, мы можем изменить всю гистограмму, разделив все счетчики вхождений на размер выборки.
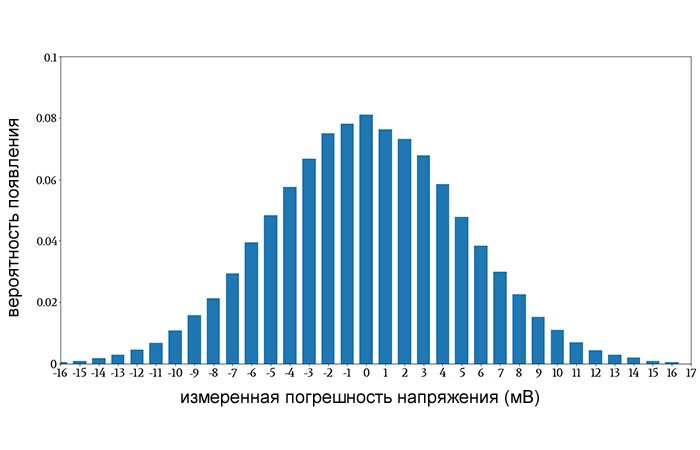
Полученный график является аппроксимацией функции массы вероятности. Например:
Всё, что мы на самом деле выполнили, это изменили числа на вертикальной оси. Тем не менее, теперь мы можем посмотреть на отдельное значение или на группу значений и легко определить вероятность появления.
Хочу прояснить следующую деталь: я сказал, что мы аппроксимируем функцию массы вероятности, когда берем гистограмму и делим значения на размер выборки. Истинная функция массы вероятности представляет собой идеализированное распределение вероятностей, что означает, что для этого потребуется бесконечное количество измерений.
Таким образом, когда мы работаем с реалистичными размерами выборки, гистограмма, созданная на основе измеренных данных, дает нам только приближение функции массы вероятности.
Масса вероятности против плотности вероятности
Стоит подчеркнуть, что функция массы вероятности является дискретным эквивалентом функции плотности вероятности (о которой мы говорили в предыдущей статье).
В то время как функция плотности вероятности является непрерывной и предоставляет значения вероятности, когда мы интегрируем функцию в указанном диапазоне, функция массы вероятности дискретизируется и дает нам вероятность, связанную с конкретным значением или интервалом.
Эти две функции передают одну и ту же общую статистическую информацию о переменной или о сигнале, но делают это по-разному.
Обратите внимание на разницу между двумя названиями: вертикальная ось функции массы вероятности указывает массу вероятности, как количественное значение. Вертикальная ось функции плотности вероятности указывает плотность вероятности относительно горизонтальной оси; чтобы определить количественное значение вероятности, мы должны интегрировать эту плотность по горизонтальной оси.
Заключение
Мы рассмотрели функции массы и плотности вероятности, и теперь мы готовы изучить кумулятивную функцию распределения и исследовать вероятности нормального распределения с точки зрения стандартного отклонения. Об этом мы поговорим в следующей статье.
Теги
ГистограммаМасса вероятностиНормальное распределение / Гауссово распределениеПлотность вероятностиСтатистикаФункция массы вероятностиФункция плотности вероятности
Авторы: , П. В. Семенов.
Издательство:
Мнемозина 2015-2020
Тип: Задачник, Базовый уровень
Подробный решебник (ГДЗ) по Алгебре за 10‐11 (десятый‐одиннадцатый) класс Учебник, Задачник – готовый ответ §50 – 4. Авторы учебника: Мордкович, Семенов, Базовый уровень. Издательство: Мнемозина 2015-2020.
Условие /
§50 / 4
50.4. По приведенной гистограмме распределения данных (рис. 76) найдите: а) количество вариант и объем измерения; б) размах и моду измерения; в) таблицу распределения данных; г) среднее результатов измерения.
Решебник №1 к задачнику / §50 / 4
Видеорешение к задачнику / §50 / 4
Решебник к учебнику / §50 / 4
Оцените решебник:
4.4/5
322
Параметры
технологического процесса, на которые
действуют множество факторов (человек,
оборудование, режущий инструмент,
материал, температура окружающей среды
и т.д.), не могут быть все время одинаковы
и изменяются в пределах, влияющих на
них погрешностей действующих факторов.
Так что неизбежно, что в любом заданном
множестве значений параметра будет
рассеивание. Но, хотя сами значения
параметра все время меняются, они
подчиняются определенной
закономерности,
которую называют распределением.
При
контроле качества изделий необходимо
на основе собранных данных выявить
реальное состояние показателей качества
изделия, по которым, сравнивая их с
требуемыми показателями, принимается
окончательное решение о годности
данного изделия. Если проверяются все
изделия, то вся их совокупность называется
генеральной популяцией или генеральной
совокупностью.
Одно
или несколько изделий, взятых из
генеральной совокупности, называется
выборкой.
Так
как выборка используется для оценивания
характеристик всей генеральной
совокупности, ее необходимо выбирать
таким образом, чтобы она отражала именно
эти характеристики. А для этого
выборка должна быть случайной. Данные,
полученные на выборках, служат основой
для решения о генеральной совокупности.
Очевидно, что чем больше объем выборки,
тем больше информации об этой
совокупности можно получить, тем
точнее она будет характеризовать всю
генеральную совокупность.
Для
оценки совокупности изделий по
случайной выборке применяют метод,
основанный на построении гистограммы
распределения.
Гистограмма
представляет собой столбчатый график
и применяется для наглядного изображения
распределения конкретных значений
параметра по частоте повторения за
некий период времени (неделя, месяц,
год).
При
нанесении на график допустимых значений
параметра определяется, как часто
этот параметр попадает в допустимый
диапазон или выходит за его границы.
Вид
гистограммы зависит от объема выборки,
количества интервалов, начала отсчета
первого интервала. Чем больше объем
выборки и меньше ширина интервала, тем
ближе гистограмма к непрерывной кривой.
Подготовка
данных для построения гистограммы.
Допустим, надо исследовать вероятность
достижения заданной точности диаметра
наружной поверхности оси, обрабатываемой
на токарном станке в размер 32,50 ±0,025. Для
этого из большого количества осей взята
выборка в количестве 90 штук. Имеется
банк измеренных диаметров осей, при
этом максимальный измеренный диаметр
равен 32,5455 мм, а минимальный-32,5005 мм.
Построим гистограмму по данным измерений
диаметров осей. Рассмотрим последовательно
этапы
подготовки данных для построения.
Этап
1–
вычислить размах выборки (R). Размах
выборки
равен разности наибольшего и наименьшего
значения измерений диаметров: R=0,045
мм.
Этап
2
– определить количество и размеры одного
интервала размаха выборки. Для
наглядности гистограммы рекомендуется
выбирать при ее
построении
от 5 до 20 интервалов равной ширины.
Для нашего случая можно принять
количество интервалов равным 9 при
ширине одного интервала 0,005 мм.
Этап
3
– подготовить бланк таблицы со
следующими графами: номер интервала,
границы интервала, среднее значение
интервала, количество измерений в
каждом интервале.
Этап
4
– определить границы интервалов. Нижняя
граница первого интервала равна
минимальному значению измерения в
выборке, а верхняя граница равна сумме
значения нижней границы и величины
интервала. Нижняя граница второго
интервала равна верхней границе первого.
И так далее до девятого интервала, у
которого верхняя граница равна
максимальному значению измеренного
диаметра.
Этап
5
-вычислить значение середины каждого
интервала. Очевидно, что средняя точка
каждого интервала имеет среднее
значение границ
интервала.
Этап
6
– заполнить таблицу на рис. ниже.
Рис.
Данные для построения гистограммы
распределения
Последовательность
шагов при построении гистограммы
такова.
Этап
1
– взять лист бумаги (лучше в клетку) и
нанести на него горизонтальную линию,
на которой будем откладывать значения
измерений диаметров осей. Масштаб по
оси выбирается из соотношения размера
листа и среднего значения размаха
выборки. Например, каждые 10 мм листа
соответствуют ширине одного интервала
0,005 мм. Нанести на горизонтальной оси
весь размах с разметкой каждого
интервала. Оставить при этом слева и
справа свободные места, равные ширине
одного интервала. Обозначить точками
середины каждого интервала.
Этап
2
– нанести на бумагу вертикальную ось.
Место пересечения с горизонтальной
осью – крайняя левая точка добавочного
(нулевого) интервала. Масштаб по оси
выбирается из соотношения размера
листа и максимального количества
измерений в одном интервале. Например,
на каждые 25 мм листа-5 измерений.
Этап
3
– построить в каждом интервале
прямоугольники, высота которых
соответствует количеству измерений
в интервале (рис. ). Построенная
столбчатая диаграмма и есть гистограмма
распределения. Нанесем на гистограмму
линию, состоящую из отрезков, соединяющих
точки середин интервалов на верхних
полках прямоугольников. Непрерывная
линия, соединяющая середины интервалов
по верхним полкам, называется полигоном
распределения.
При увеличении количества интервалов
и уменьшении их ширины полигон
распределения превращается в практическую
кривую распределения. Расстояние
между крайними точками первого и
последнего интервала называется
размахом
или полем рассеивания.
Рис.
Гистограмма: x‾
– среднее значение, s
– среднеквадратическое отклонение, 1
– полигон распределения.
Сравнение
гистограммы с границами допуска. При
сравнении и анализе величин и взаимного
положения полей допуска и рассеивания
можно выделить 5 типичных вариантов.
Первый
вариант.
Поле рассеивания значительно меньше
поля допуска, ω < Т (рис.10.11, а).
Технологический процесс протекает
нормально, требуется только поддерживать
существующее состояние.
Рис.
Сравнение гистограммы с границами
допуска (SL–SU):
а), б) – технологический процесс протекает
нормально, в),г),д) – технологический
процесс протекает ненормально.
Второй
вариант.
Поле рассеивания равно или немного
меньше поля допуска, ω = Т (рис. 10.11, б).
Технологический процесс протекает
нормально, но нет запаса надежности.
Можно провести мероприятия по уменьшению
поля рассеивания, если затраты на эти
мероприятия будут меньше, чем потери
от возможного брака.
Третий
вариант.
Поле рассеивания меньше поля допуска,
но смещено влево (или вправо) от границы
поля допуска (рис.10.11, в). Процесс
ненормальный. Необходимо добиться
смещения середины поля рассеивания
к центру поля допуска.
Четвертый
вариант.
Поле рассеивания больше поля допуска
(ω > Т) и размещено симметрично
относительно центра поля допуска (рис.
10.11, г). Процесс ненормальный. Необходимо
провести мероприятия по уменьшению
поля рассеивания.
Пятый
вариант.
Поле рассеивания больше поля допуска
и смещено относительно центра допуска
(рис.10.11, д). Процесс ненормальный. Это
худший вариант взаимного положения
полей, при котором количество
забракованных изделий возрастает.
Необходимо, прежде всего, добиться
симметричного расположения полей,
посчитать затраты от брака и принять
(или не принять) дополнительные мероприятия
по уменьшению поля рассеивания.
Для
нашего конкретного примера допуск на
диаметр составляет 0,05 мм, а поле
рассеивания 0,045 мм. Таким образом, поле
рассеивания меньше величины поля
допуска. Одновременно минимальное и
максимальное измеренные значения
диаметров меньше соответствующих
минимальной и максимальной границ
поля допуска. Можно сделать заключение,
что операция точения обеспечивает
необходимую точность диаметра наружной
поверхности оси. Однако разница между
величинами полей невелика, что при
малейшей неточности в настройке
технологической системы может привести
к появлению брака.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #