Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней

Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами ![]() . Последний
. Последний ![]() элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.

Обозначим элементы нашей выборки через переменные ![]()
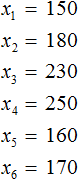
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
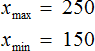
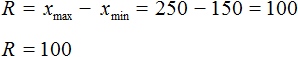
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
![]()
Вернемся к нашему примеру

Узнаем сколько в среднем мы тратили в каждом из шести дней:
![]()
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
![]()
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
![]()
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
![]()
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:
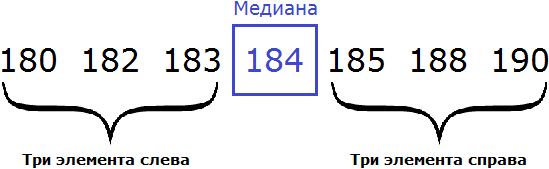
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186
![]()
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
![]()
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
![]()
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
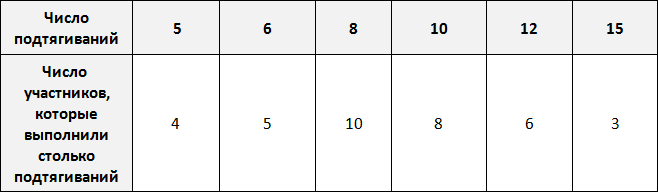
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Урок 282
Тема урока: Задачи математической статистики.
Цели урока:
Обучающая:
Научить учащихся решать задачи по обработке
статистических данных, используя понятия:
объём измерения, размах измерения, мода
измерения, среднее арифметическое, медиана
измерения, варианта измерения, кратность
варианты, и составлять данные в виде таблиц,
диаграмм, графиков. Ввести понятия: частота
варианты, частота варианты (в процентах).
Развивающая:
Формировать умения
учащихся, решать задачи на
обработку статистических данных, используя
данные в виде таблиц, диаграмм, графиков.
Развивать логическое и математическое мышление.
Воспитывающая:
Воспитывать культуру речи,
построения плана
ответа, сознательной дисциплины, культуры
конструктивного мышления, активность на уроке,
аккуратность при выполнении записи на доске и в
тетради, положительный интерес к изучаемому
предмету.
Тип урока: Комбинированный.
Вид
урока: Урок
решения задач на обработку статистических
данных, используя данные в виде таблиц,
диаграмм, графиков.
Методы
обучения: Репродуктивный.
Материально-техническое
оснащение:
–Математика Учебник Общеобразовательные
дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва Издательский центр «Академия» 201
–Математика Учебник
Общеобразовательные дисциплины
для профессий и специальностей социально-экономического
профиля. Авторы В.А. Гусев, С.Г.Григорьев, С.В.Иволгина
Москва Издательский центр «Академия» 2011
– Математика Задачник Общеобразовательные
дисциплины
Начальное и среднее профессиональное образование
Автор М.И. Башмаков.
Москва
Издательский центр «Академия» 2012
– дидактический
раздаточный материал (карточки для
индивидуальной
работы)
Ход урока
1. Организационный момент урока
– сдача рапорта
2. Целевая ориентация
(
Преподаватель формулирует тему, цели и задачи урока. Мотивирует учащихся к
учебной деятельности. Разъясняет последовательность этапов урока, приводящих к
достижению цели)
3. Проверка
домашнего задания.
4. Вопросы для закрепления изученного
материала.
1). Перечислить
основные этапы простейшей статистической обработки данных.
2). Что называют
объемом измерения?
3). Что такое размах
измерения?
4). Что называют
модой измерения?
5). Что называют
средним арифметическим?
6). Что называют
вариантой измерения?
7). Что называют
медианой измерения?
5.
Формирование
навыков умственного труда
Решение задач у доски
Задача 1
В таблице распределения данных часть информации была утеряна.
Восстановить ее. Если известно, что объем измерения равен 20, размах измерения
равен 6, а мода равна 2.
|
|
Сумма |
|||||
|
– 1 |
0 |
3 |
||||
|
Кратность |
5 |
1 |
7 |
3 |
Решение
По определению. В графе «Сумма» должен стоять объём измерения, т.е. 20.
Этот объём равен сумме всех кратностей, значит, кратность варианты «0», равна
20 – (5+1+7+3) = 4.
Самая большая кратность равна 7. Значит, над ней и расположена мода
измерения, равная 2. Так как размах равен 6, а наибольшая варианта равна 3, то
наименьшая варианта равна 3 – 6 = – 3. эту варианту помещаем в последнюю
свободную графу над кратностью 5.
Ответ:
|
|
Сумма |
|||||
|
– 3 |
– 1 |
0 |
2 |
3 |
||
|
Кратность |
5 |
1 |
4 |
7 |
3 |
20 |
Задача 2
По приведённой гистограмме распределения данных найти: количество
вариант измерения, объем, размах. моду измерения, наиболее удалённую от моды
варианту и ее кратность. Составить таблицу распределения данных.

Решение.
Количество вариант – это количество столбиков в гистограмме, т.е. 7.
Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот
всех семи столбиков: 3+2+7+3+5+4+1 = 25. Таблица распределения выглядит так:
|
|
Сумма |
|||||||
|
2 |
4 |
5 |
6 |
7 |
9 |
10 |
||
|
Кратность |
3 |
2 |
7 |
3 |
5 |
4 |
1 |
25 |
1). Наибольшая варианта равна 10, а наименьшая равна 2.
2). Размах равен 8. (10 – 2) =8.
3). Мода измерения равна 5, так как она встречалась чаще других – 7
раз.
4). На наибольшем расстоянии от моды находится варианта 10, её
кратность равна 1.
Определение: Если кратность варианты разделить на объем измерения,
то получится частота варианты. Это число показывает, какую
часть (долю) среди всех данных составляют данные, равные выбранной варианте.
Частоту варианты можно измерить и в процентах.
Частота варианты
(в процентах) =
Задача 3
В десятых классах трёх школ микрорайона провели проверочный диктант по
русскому языку. По их результатам изображена гистограмма распределения
полученных отметок.

а) Найти: общее
количество работ, частоту пятёрок, процентную частоту
двоек.
б) Заполнить сводную таблицу распределения данных.
в) Построить гистограмму распределения частот ( в процентах).
г) Построить круговую диаграмму распределения частот (в процентах).
Решение.
а) На гистограмме указано, что двоек было 40, троек – 50, четвёрок –
75, пятёрок – 35. значит. Всего было 200 работ. Это есть объём измерения.
Частота пятёрок равна ![]() , а частота (в процентах) двоек
, а частота (в процентах) двоек
равна ![]()
б) Так как все кратности известны, то можно заполнить всю таблицу
распределения:
|
|
Сумма |
||||
|
2 |
3 |
4 |
5 |
||
|
Кратность |
40 |
50 |
75 |
35 |
200 |
|
Частота |
0,2 |
0.25 |
0.375 |
0,175 |
1 |
|
Частота,% |
20 |
25 |
37,5 |
17,5 |
100 |
в) Для построения гистограммы распределения частот (в процентах)
используем первую и четвёртую строки. Получим четыре вертикальных столбика.
Основания которых соответствуют полученным отметкам, а высоты равны найденным
частотам ( в процентах).

г) разделим круг на четыре сектора. Центральный угол сектора двойки
составляет 20% от 3600. т.е. 720. Центральный угол
сектора тройки составляет 25% от 3600, это прямой угол. Центральные
углы секторов четвёрки и пятёрки равны соответственно 1350 и 630.

5. Вопросы для
закрепления изученного материала.
1). Что называют частотой
варианты?
2). По какой формуле
измеряют частоту варианты в процентах?
6. Итог урока.
Домашнее задание.
Задача.
По приведённой гистограмме распределения данных найти:
а) количество вариант и объем измерения;
б) размах и моду измерения;
в) таблицу распределения данных;
г) среднее результатов измерения.

Решение.
1) Количество вариант – это количество столбиков в гистограмме, т.е. 9.
Объем измерения равен сумме кратностей всех вариант, т.е. равен сумме высот
всех девяти столбиков: 5+6+3+7+4+11+5+4+5 = 50. Таблица распределения выглядит
так:
|
|
Сумма |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
Кратность |
5 |
6 |
3 |
7 |
4 |
11 |
5 |
4 |
5 |
50 |
2). Наибольшая варианта равна 10, а наименьшая равна 2.
Размах равен 8. (10 – 2) = 8.
Мода измерения равна 7, так как она встречалась чаще других – 11 раз.
3). Таблица распределения выглядит так:
|
|
Сумма |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
Кратность |
5 |
6 |
3 |
7 |
4 |
11 |
5 |
4 |
5 |
50 |
4). Среднее арифметическое
– это частное от деления суммы всех результатов измерения на объём измерения.
Среднее удобно вычислять после того, как составлена таблица распределения. В
данном случае вычисления выглядят так:

Дата публикации: 09 апреля 2017.
Урок и презентация на тему: “Математическая статистика, элементы статистики”
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Математическая статистика, элементы статистики (PPTX)
Статистика, введение
Темой сегодняшнего урока будет математическая статистика.
Этот предмет занимается статистикой, используя различные математические методы. Математическая статистика – это самостоятельно развивающийся раздел математики, в котором существуют и свои уникальные способы решения различных задач.
Так чем же занимается и для чего нужна математическая статистика?
Предположим, что у учеников девятых классов измерили рост. Как представить полученные данные? Можно записать их в строчку друг за другом, можно разделить данные по классам, можно попробовать создать таблицу. Все эти способы довольно громоздки и неудобны. Будет сложно извлечь информацию из такого набора чисел. А теперь представьте, что измерили рост учеников девятых классов всех школ в городе. Количество измерений может перевалить за тысячу.
Математическая статистика занимается обработкой данных и представлением их в виде удобном для восприятия. Это только одна из задач статистики. Построение прогнозов и оценок; применение различных методов исследования; достоверность проведенных испытаний и многое другое – вот чем занимается статистика.
Как же обрабатывает информацию статистика?
- Данные измерений упорядочивают и группируют.
- Составляют таблицы распределений данных.
- По таблицам строят графики распределений.
- В итоге создается паспорт измерений, в котором собраны числовые характеристики полученной информации.
Давайте рассмотрим эти пункты.
Упорядочивание и группировка данных
Первое, что необходимо сделать при анализе данных, определить рамки, в которых находится исследователь. Выбираются наименьшее и наибольшее допустимые значения, которые могут не совпадать с полученными данными. Например, при измерении роста учеников, шансов, что кто-то будет ниже 140 сантиметров и выше 200 сантиметров очень мало. Если найдется такой вариант, то данные статистики можно подкорректировать.
При измерении роста могут получиться числа: 140,150,160,170,180,190,200 – это общий ряд данных, которые принято располагать в порядке возрастания. Общий ряд данных может быть и другим, например: 140,145,150,155,160,…,190,195,200. Как представить общий ряд данных зависит от конкретной задачи.
Пример. Составить общий ряд данных, включающих:
а) месяцы рождения одноклассников,
б) годов рождения родственников и друзей,
в) буквы, с которых начинается слово.
Решение.
а) Всего месяцев 12, если их перечислить по цифрам, то получим общий ряд: 1,2,3,4,5,6,7,8,9,10,11,12.
б) Шанс, что кто-то из родственников старше 100 лет – мал, а что, кто-то родился в этом году – есть. Тогда общий ряд годов рождения можно составить так: 1910,1911,1912,…, 2009,2010,2011,2012,2013,2014.
в) Слово может начинаться с любой буквы алфавита, кроме ь, ы, ъ. Тогда возможны 30 вариантов, если их представить численным рядом, то получим: 1,2,3,4,…,28,29,30.
Понятие “общий ряд” не является строгим, в примере б) мы могли начать ряд с 1900 года, ряд так же назывался “общим”.
При проведении эксперимента данные из общего ряда могут не встретиться. Вернемся к нашему примеру б) и рассмотрим конкретный случай.
Вова назвал года рождения родственников: 1935,1937,1960,1965,1980,1981,1997,2005.
Общий ряд представлял собой последовательность: 1910,1911,1912,…,2009,2010,2011,2012,2013,2014.
У Вовы встретились конкретные измерения, которые называются “вариантой измерения”.
Варианта измерения – это возможный вариант проведенного измерения.
Если все варианты измерений перечислить по порядку, то получится ряд данных измерения.
Для нашего примера составим таблицу:

Пример. Выписать ряд, состоящий из букв, которые встречаются в словах: мама, папа, брат, сестра, бабушка, дедушка, тетя, дядя.
Решение. Ряд будет выглядеть так: а, б, д, е, к, м, п, р, с, т, у, ш, я. Встретились 13 букв из 33.
Некоторые буквы встречаются несколько раз, например, буква а – девять раз, другие – реже.
Определение. Если среди всех данных конкретного измерения одна из вариант встретилась ровно к раз, то число к называют кратностью измерения.
В этом примере буква а имеет кратность – 9.
Запишем кратности для каждой из букв:

Далее варианты нужно сгруппировать. Создадим сгруппированный ряд данных:
а,а,а,а,а,а,а,а,а,б,б,б,д,д,д,д,е,е,е,к,к,м,м,п,п,р,р,с,с,т,т,т,т,у,у,ш,шя,я,я.
Число повторений каждой варианты равно кратности варианты.
Составление таблицы распределения данных

Если сложить все кратности, получится количество всех данных измерения или объем измерения. Объем измерения равен количеству букв встречающихся в наших словах. Для проверки всегда складывают кратности, сумма должна равняться количеству элементов измерения.
Далее вычисляют частоту варианты.
Частота варианты=Кратность варианты/Объем измерения.
Составим таблицу частот измерений:

Сумма всех частот всегда равна единице, так как это сумма всех дробей с одинаковым знаменателем, а сумма всех числителей как раз и равна знаменателю. Для удобства, часто переводят частоты в проценты от объема измерения. Составим таблицу еще одну таблицу, каждую частоту в новой строке помножим на 100.

Графическое представление данных
Давайте построим графики функций распределения по таблицам. Договоримся, что вместо букв будем использовать цифры 1,2,3,…,13.
Тогда наша таблица примет вид:

По оси абсцисс отложим цифры, соответствующие буквам, а по оси ординат – значения частот появления варианта. Графическое изображение имеющейся информации – график распределения частот.
Таблица значений:

График распределения частот:

График распределения частот также называют полигоном распределения.
Давайте построим график распределения частот процентов. Его тоже называют полигоном распределения процентов.
Таблица значений.

Полигон распределения процентов:

Даже не большая по объему данных задача, представляет собой довольно таки утомительную процедуру подсчета и составления таблиц и графиков распределений.
Числовые характеристики данных измерения
Наши данные обладают уникальными числовыми характеристиками. Давайте определим некоторые из них.
Разность между максимальной и минимальной вариантой называют размахом измерения.
На наших графиках – это область определения (разность крайнего правого значения и крайнего левого значения на оси абсцисс). В нашем примере размах равен $13-1=12$.
Варианта, которая встречается чаще других, называется модой. В нашем примере это буква а или число 1, в зависимости от обозначения.
Если у нас есть таблица распределения частот, то в строчке частот ищем наибольшее число, и смотрим, какому варианту оно соответствует. На графике, это точка в которой достигается максимальное значение.
Наиболее важная характеристика – среднее значение (среднее арифметическое или просто среднее).
Чтобы найти среднее значение нужно:
а) Просуммировать все данные измерения.
б) Полученную сумму разделить на количество вариантов.
Для нашего примера найдем среднее значение:
$frac{1*9+2*3+3*4+4*3+5*2+6*2+7*2+8*2+9*2+10*4+11*2+12*2+13*3}{40}=5,775$.
Среднее значение можно найти другим способом:
а) Каждую варианту умножить на ее частоту.
б) Сложить получившиеся значения.
Подсчитаем этим способом:

1*0,225+2*0,075+3*0,1+4*0,075+5*0,05+6*0,05+7*0,05+8*0,05+9*0,05+10*0,1+11*0,05+12*0,05+13*0,075=5,775.
Давайте рассмотрим еще один пример.
На экзамене по математике 25 учеников 9 класса получили такие оценки:
5,4,3,3,5,4,3,3,4,4,5,5,2,2,5,5,5,3,3,4,5,5,4,3,2.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
Решение.
Возможны такие оценки: 1,2,3,4,5 – общий ряд данных.
В нашем примере встречаются оценки: 2,3,4,5 – ряд данных, все числа в ряде – варианты измерений.
Составим сгруппированный ряд: 2,2,2,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5.
б) Объем измерения равен 25, так как 25 оценок выставлено.
Составим таблицу:

в) Нарисуем графики:
Полигон распределения данных:

Полигон распределения частот:

Полигон распределения частот процентов:

Все графики похожи между собой, различия только в масштабе оси ординат.
г)Найдем среднее значение:
$2*0,12+3*0,28+4*0,24+5*0,36=0,24+0,84+0,96+1,8=3,81$.
Мода: чаще всего встречается оценка пять, она и будет модой.
Размах: $5-2=3$.
Задачи статистики для самостоятельного решения
1.На экзамене по математике 50 учеников 9 класса получили такие оценки:
5,3,4,4,5,4,3,2,4,3,5,1,2,3,5,4,5,3,3,4,5,5,4,3,1,3,4,5,4,3,2,2,1,4,4,5,5,4,4,5,3,3,3,2,1,5,4,3,2,5.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.

3. Графическое представление информации.Распределение данных измерения рационально задавать в табличном виде. Однако нам известно, что и для функций есть табличный способ их задания. Таблицы являются связующим звеном. С их помощью осуществляется переход от распределения данных к функциям и графикам.
График распределения выборки является графическим представлением информации. Согласно табличным сведениям из примеров выше отметим точки, у которых абсциссы — это номер варианта, а ординаты — кратность. Соединяем отрезками полученные точки:
Пример:

Получили многоугольник или полигон распределения данных. Собственно, polygon и переводится как «многоугольник».
Чтобы представить большой объём информации в графическом виде, можно использовать гистограммы или столбчатые диаграммы.
Пример:


4. Числовые характеристики данных измерения.
У любого из нас имеются не только данные о рождении, но и ряд иных свойств и качеств.
Такие измерения имеют свои числовые характеристики.
Размах измерения — это разность между максимальной и минимальной вариантами.
Мода измерения — вариант, который в измерении встречался чаще других.
Медиана — число, стоящее в середине сгруппированного ряда.
Среднее значение — среднее арифметическое, или просто среднее. Для нахождения среднего значения нужно:
1) вычислить сумму всех данных измерения;
2) полученную сумму разделить на количество данных.
Вопросы
занятия:
•
рассмотреть основные этапы статистической обработки данных;
•
познакомиться с понятием «дисперсия»;
•
рассмотреть примеры вычисления дисперсии с помощью специального алгоритма.
Материал
урока
Слово
статистика происходит от латинского «статус», означающего «состояние дел».
Этому
понятию можно дать следующее определение.
Статистика
–
отрасль знаний, в которой излагаются общие
вопросы сбора, измерения и анализа массовых статистических (количественных или
качественных) данных; изучение количественной
стороны массовых общественных явлений в числовой форме.
Рассмотрим
пример.
Анализируя
результаты написания контрольной работы по математике, учитель сгруппировал все
данные таким образом.
Только
1 человек получил двойку. Десять получили тройку. Пятеро человек написали
контрольную на 4. И только двое получили пятёрки.
Всю
эту информацию можно собрать в одной таблице.
Также
эти данные можно представить графически.
На
горизонтальной оси отметим все возможные результаты, а на вертикальной — их
количество.
Так
точки 2 1, 3 10, 4 5 и 5 2 будут соответствовать парам значений из таблицы.
Соединим их ломаной. Так мы с вами получили многоугольник распределений.
А
теперь для каждой пары значений изобразим соответствующий столбец и раздуем его
до ширины равной одному. Получаем столбчатую диаграмму — гистограмму
распределений.
Рассмотрим
ещё один способ.
Представим
все данные в виде круга.
Так
получается круговая диаграмма.
Сейчас
мы с вами на конкретном примере разобрали основные этапы статистической
обработки данных.
К
этим трём этапам обычно добавляют ещё один: получение паспорта данных
измерений, состоящий из нескольких числовых характеристик.
К
этим характеристикам относят объём, размах, моду и среднее измерение.
Объём
измерения в данном случае равен 18, так как обрабатывались
результаты восемнадцати учеников.
Размах
измерения равен 9. Это разница между наибольшим и наименьшим
результатами.
Мода
измерения — это самый популярный, «модный» результат. В
данном случае она равна 3.
Среднее
(или среднее арифметическое). Это частное суммы всех результатов
измерений на объём измерений.
Чаще
всего, как вы понимаете, результатами измерений являются числа. Каждое число,
встретившееся в конкретном измерении, называют вариантой измерения.
Если
записать все варианты измерений, то получится ряд данных измерения.
Если
записать их в порядке возрастания, то получим сгруппированный ряд данных.
Среднюю
варианту называют медианой измерения. Если их две, то медиана равна их среднему
арифметическому.
В
нашем примере средними вариантами являются варианты под номерами 9 и 10. Они
обе равны 3, значит, и медиана равна 3.
Определение.
Каждая
варианта встречается некоторое число раз, его называют кратностью данной
варианты.
Для
нашего примера таблица распределения данных примет такой вид.
Применим
полученные знания при решении задачи.
На
уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их
результаты. Получился такой ряд данных
Требуется
сгруппировать данные, составить таблицу их распределения, а также найти объём,
размах, моду, среднее и медиану измерения.
Для
начала сгруппируем данные, расположив их в порядке возрастания.
Это
позволит нам составить таблицу распределения данных.
Теперь
найдём объём измерения.
Размах
измерения равен разности наибольшей и наименьшей вариант.
Среднее
значение равно частному суммы всех полученных значений и объёма измерения.
Мода
измерения равна 125. Ведь это самый популярный результат.
Для
отыскания медианы нужно найти среднюю варианту в сгруппированном ряду данных.
Их две и обе равны 125. Значит, медиана равна 125. Так мы с вами составили
паспорт данных.
А
теперь, по полученной таблице распределения данных построим многоугольник
распределения и гистограмму распределения.
Мы
имеем 5 вариант: 110, 120, 125, 130 и 140.
Кратность
первой варианты равна 2, второй — 3, третьей — 5, четвёртой — 3, и пятой —1.
Соединив
полученные точки, получим многоугольник распределения данных.
Тогда
гистограмма примет такой вид.
Обратите
внимание, варианты могут располагаться неравномерно на оси Ox,
между ними могут быть пропуски.
Например,
значение 115 не встретилось ни разу, то есть её кратность равна 0. Очевидно,
что такое значение не может быть вариантой.
Для
построение гистограммы можно было использовать номинативную шкалу, то есть по
горизонтали распределить номинации, варианты, а на вертикальной оси оставить
значения их кратностей. Гистограмма примет такой вид.
В
этом случае вариантами могут быть не только числа.
Если
кратность варианты разделить на объём измерения, то получится частота варианты.
Найдём
частоту каждой варианты данной задачи. Обратите внимание, сумма частот
всегда равна единице.
Частоту
также можно выразить в процентах. Сумма частот в процентах, очевидно, всегда
равна 100.
Только
что с помощью таблицы распределения данных мы составили таблицу распределения
частот.
Выполним
задание.
А
теперь рассмотрим такой случай.
Пример.
Определение.
Числовую
характеристику данных измерения, отвечающую за разброс данных вокруг среднего
значения, называют дисперсией D.
Определение.
Средним
квадратическим отклонением называют:
Чем
меньше эти значения, тем плотнее группируются данные измерения вокруг среднего
значения.
Существует
алгоритм вычисления дисперсии данных.
Воспользуемся
этим алгоритмом и найдём значение дисперсии результатов отклонения для каждого
ружья.
Проведём
подсчёты для ружья А. Их удобно производить в таблице.
Найдём
их среднее значение. Получаем, что дисперсия равна:
А
среднее квадратическое отклонение равно:
Вычислим
значение дисперсии для ружья Б.
Можем
вычислить дисперсию как среднее квадратов отклонений.
Тогда
среднее квадратическое отклонение равно:
Видим,
что дисперсии отличаются практически в 7 раз, а средние квадратические
отклонения примерно в 3 раза.
Можно
сказать, что ружьё Б стреляет с разбросом в 3 раза большим, чем ружьё А.
Поэтому ружьё А точнее.
Подведём
итоги нашего урока.
Сегодня
вы познакомились и рассмотрели на примерах этапы статистической обработки
данных.
Каждое
значение, полученное в ходе измерений, мы договорились называть вариантой.
А число повторений данной варианты, называют её кратностью.
Вы
познакомились с формулой отыскания частоты варианты. И научились составлять
таблицу распределения частот.
Также
узнали, что числовую характеристику данных измерения, отвечающую за разброс
данных вокруг среднего значения, называют дисперсией.
А
ещё, рассмотрели примеры нахождения этих величин с помощью специального
алгоритма.
