В этой статье мы рассмотрим, как узнать размер словаря в Python .
Размер словаря может означать его длину или место, которое он занимает в памяти. Чтобы найти количество элементов, хранящихся в словаре, мы можем использовать функцию len()
Чтобы узнать размер словаря в байтах, мы можем использовать getsizeof() модуля sys
Чтобы подсчитать элементы вложенного словаря, мы можем использовать рекурсивную функцию.
Определение размера словаря
Функция len() широко используется для определения размера объектов в Python. В нашем случае передача объекта словаря этой функции вернет размер словаря, то есть количество пар ключ-значение, присутствующих в словаре.
Поскольку эти объекты отслеживают свою длину, эта операция имеет временную сложность O (1):
Приведенный выше фрагмент возвращает следующий результат:
Определение размера словаря в байтах
Размер памяти объекта словаря в байтах можно определить с помощью функции getsizeof() . Эта функция доступна из модуля sys Как и len() , его можно использовать для определения размера любого объекта Python.
Это особенно полезно, когда нам нужен код, который должен быть эффективным и / или требует регулярного мониторинга. Давайте возьмем наш предыдущий пример и получим размер словаря в байтах вместо количества элементов:
Определение размера вложенных словарей
Вложенный словарь — это словарь внутри словаря или словарь с несколькими уровнями пар ключ-значение. Эти вложенные словари помогают упростить сложные структуры, такие как ответы JSON от API.
Они выглядят примерно так:
Использование len() для подсчета всех пар ключ-значение не сработает, поскольку дает размер объекта только для первого уровня ключей. Чтобы найти количество всех вложенных ключей, мы можем написать специальную рекурсивную функцию для подсчета ключей. Эта функция принимает словарь и счетчик в качестве аргументов и выполняет итерацию по каждому ключу.
Для каждой итерации функция проверяет, является ли рассматриваемый экземпляр ключа словарем. Если это правда, функция снова рекурсивно вызывается путем добавления переменной counter+1 и передачи оцениваемого словаря в качестве аргументов.
Эта рекурсивная функция завершается после полной итерации, возвращая длину словаря как переменную: counter .
Если ключ не является экземпляром словаря, счетчик просто добавляется к counter+1 . Функция возвращает counter в результате итерации, которая дает размер оцениваемого словаря.
Следовательно, количество вложенных ключей оценивается с помощью этой функции, как показано ниже:
И когда фрагмент выполняется, мы получаем следующий вывод, соответствующий количеству ключей, присутствующих в словаре:
Заключение
В этой статье мы изучили методы расчета размера и длины словарей и вложенных словарей.
Эти функции могут быть очень полезны при обслуживании объектов JSON через API: существуют ограничения, налагаемые веб-серверами на размер объектов JSON, обслуживаемых через API, и эти функции могут использоваться для контроля длины и размера.
dict (словарь)
obj — Первым необязательным позиционным аргументом может являться отображение или итерирующийся объект (при этом каждый его элемент должен быть тоже итерирующемся и содержать ровно два объекта).
**kwargs — Поддерживаются также необязательные именованные аргументы. При использовании вкупе с позиционными аргументами и совпадении ключей значениями из именованных пользуются приоритетом.
Словари являются отображениями.
Словари являются изменяемыми объектами.
Объявление
В коде словари могут быть объявлены при помощи фигурных скобок — .
Кроме того, можно объявить их при помощи конструктора dict().
Ключи
Ключами словаря могут являться только объекты, поддерживающие хеширование. Таким образом, использовать в качестве ключей списки, словари и другие изменяемые типы не получится.
Если в словарь будут добавлены несколько значений с одним и тем же ключом, словарь сохранит последнее.
Порядок ключей
Данные в обычном словаре упорядочены по очередности добавления ключей, начиная с +py3.6 (в +py2.7 — не упорядочены, но последовательность детерминирована, воспроизводима; в +py3.5 — не упорядочены, последовательность не детерминирована, не воспроизводима между запусками).
Если требуется хранить порядок, в котором в словарь были добавлены элементы (например для обхода этих элементов), следует использовать collections.OrderedDict().
Значения
В качестве значений могут использоваться любые объекты.
Получение значений
Доступ к значениям производится при помощи ключей.
Если ключ отсутствует в словаре, возбуждается исключение KeyError.
+py2.5 Чтобы изменить это поведение можно в наследнике dict определить метод __missing__(key), в котором описать нужные действия при отсутствии ключа.
Установка значений
Кроме установки значений при создании словаря, можно дополнять его по мере надобности.
Определение наличия/отсутствия элемента
+py2.2 Определить, присутствует ли ключ в словаре можно при помощи конструкции in.
+py2.2 Определить, отсутствует ли ключ в словаре можно при помощи антонимичной конструкции not in.
Количество элементов в словаре
Количество элементов можно получить, используя функцию len().
Детали реализации CPython
Словари реализованы при помощи динамических хеш-таблиц. По сравнению с двоичными деревьями, это, в большинстве случаев, даёт выигрыш при получшении значений (наиболее часто используемая операция); кроме этого упрошается реализация.
Для каждого ключа при помощи функции hash() вычисляется хеш-код. Код этот широко варьируется в зависимости от ключа и данных процесса (например, хеш для «Python» может быть -539294296 , в то время как для «python» — отличается от первого одним битом — он будет 1142331976 ). Хеш используется для определения места (во внутреннем массиве), где хранится значение. В случае если все используемые вами ключи будут иметь различные хеши, для получения значения по ключу будет затрачено постоянное время — O(1).
Топ-10 методов словарей в Python
Словарь в Python используется для хранения наборов данных в виде пар ключ-значение. Он работает как ассоциативный массив, который встречается в других языках программирования. Для определения словаря используются фигурные скобки , а пара «ключ-значение» определяется при помощи двоеточия : . Содержимое ключа и значения может быть как числовым, так и строковым.
Для работы со словарями Python имеет множество встроенных методов. С их помощью решаются задачи добавления и удаления элементов, обновления, поиска, подсчета и т.д. В этой статье мы расскажем про десять самых важных, на наш взгляд, методов словарей в Python.
Метод items()
Метод items() используется для возврата списка кортежей с парами всех ключей и значений словаря.
Данный метод не принимает никаких аргументов.
Приведем пример использования данной функции.
Объявлен словарь с именем products . Ключи содержат названия продуктов, а значения — их цены. Используем для нашего словаря метод items() и сохраним в другой переменной с именем itemlist , а затем выведем на экран.
Выполнив данную программу, получим следующий результат:
Метод keys()
keys() используется для возврата списка со всеми ключами словаря.
Этот метод также не принимает никаких аргументов.
Давайте рассмотрим метод keys() на примере. В скрипте объявлен словарь с именем products . Как и в предыдущем примере, ключи содержат названия продуктов, а значения — их цену. Применим метод keys() , а возвращаемые значения сохраним в переменной с именем keylist , которую затем выведем на экран.
Если вам нужен список всех значений словаря, следует использовать метод values() , который работает аналогичным образом.
Метод setdefault()
setdefault() используется для получения значения любого конкретного ключа из словаря, если такой ключ существует. Этот метод можно использовать для установки значения по умолчанию, если указанного ключа в словаре нет.
Синтаксис: dictionary.setdefault(key_value [, default_value])
У этого метода два аргумента. Первый является обязательным и используется для указания ключа, по которому будет выполняться поиск в словаре. Второй аргумент опционален. Он используется для установки значения по умолчанию, если ключа, указанного в первом аргументе, не окажется в словаре. Если указанного ключа в словаре нет, а значение по умолчанию не определено, метод вернет «None».
Следующий пример показывает использование метода setdefault() в словаре. Возьмем все тот же словарь products . Для начала используем метод setdefault() с одним аргументом. Сохраним его в переменную с именем juice_price и выведем эту переменную на экран.
Ключ Mango Juice существует в словаре. Значение этого ключа 30, оно и выводится на экран.
А теперь давайте используем этот метод с двумя аргументами, сохраним в переменную с именем cake_price и выведем ее.
Выполним данный код и получим следующее:
Ключа Cake в словаре нет. Поэтому печатается значение по умолчанию для метода setdefault() , в нашем случае это 35.
Метод get()
Метод get() работает аналогично методу setdefault() , но между ними есть одно различие. Для метода get() оба аргумента являются обязательными, в то время как в методе setdefault() второй аргумент опционален.
Синтаксис: dictionary.get(key_value , default_value)
Данный метод возвращает значение, соответствующее указанному ключу (ключ задается в первом аргументе). Если же такого ключа в словаре не окажется, метод вернет значение по умолчанию, которое мы задаем во втором аргументе.
В следующем примере используется тот же словарь, что и во всех предыдущих. Здесь метод get() используется дважды, с двумя разными значениями ключа.
Первый ключ, переданный в метод get() , — Chocolate . Его нет в словаре, поэтому выводится значение по умолчанию.
Второй ключ, который мы передали в метод get() , — это Mango Juice . Такой ключ в словаре есть, поэтому на экран выводится его значение.
Метод len()
Метод len() используется для подсчета общего количества элементов в словаре (под элементом понимается пара ключ-значение).
Этот метод принимает словарь в качестве аргумента и возвращает общее количество элементов этого словаря.
Давайте рассмотрим данный метод на примере. Следующий скрипт подсчитывает общее количество элементов словаря products и выводит на экран это значение.
Выполнив данный код, получим, что наш словарь состоит из 4 элементов:
Метод pop()
Метод pop() используется для получения конкретного значения по ключу и удаления этого элемента из словаря на основе значения ключа.
Синтаксис: dictionary.pop(key [, value])
У этого метода два аргумента. Первый аргумент является обязательным и используется для указания ключа. Второй аргумент опционален. Он используется для установки значения по умолчанию, которое будет возвращено, если указанного в первом аргументе ключа не окажется в словаре.
Для лучшего понимания рассмотрим пример. Объявим словарь с именем dictvar , содержащий четыре элемента.
Сначала используем в качестве ключа Phone , а дополнительное значение указывать не будем.
Ключ Phone в словаре есть. Поэтому при использовании метода pop() возвращается его значение, после чего этот элемент удаляется из словаря.
А теперь давайте применим метод pop() с тем же первым аргументом ( Phone ), но к нему добавим и второй, необязательный аргумент.
При втором вызове метода pop() мы использовали тот же первый аргумент, но такой элемент уже был удален из словаря предыдущим pop() . Поэтому возвращается значение, заданное в опциональном аргументе метода pop() .
Метод update()
update() используется для двух словарей. Если какой-либо ключ второго словаря совпадает с любым ключом первого словаря, то значение ключа из первого словаря будет обновлено значением этого же ключа из второго словаря. Ключи второго словаря, не совпадающие ни с одним ключом из первого словаря, добавляются в конец первого словаря вместе со своими значениями.
В качестве аргумента метод принимает dictionary2 , который будет использоваться для обновления dictionary1 .
Рассмотрим пример. В следующем скрипте объявлены два словаря: dict1 и dict2 . dict2 используется для обновления dict1 с помощью метода update() . dict1 печатается до и после использования метода update() .
Запустим наш код. Вывод:
У словарей dict1 и dict2 есть один общий ключ, это 01113456 . Поэтому значение этого ключа в dict1 обновляется значением из dict2 . Второй ключ dict2 не существует в dict1 , поэтому этот элемент добавляется в конец dict1 .
Метод copy()
copy() используется для создания копии словаря. Это полезно, когда нам нужно сохранить исходную копию словаря перед изменением.
Этот метод не принимает никаких аргументов.
Рассмотрим пример. В следующем скрипте dict1 копируется в dict2 . Обе переменные используют разную память. Таким образом, если вы измените какое-либо значение одного словаря, это не повлияет на другую копию словаря. Изменим одно из значений dict2 и выведем оба словаря.
Запустим наш код. Можно заметить, что изменения в dict2 не вызывают никаких изменений в dict1 .
Метод sorted()
sorted() используется в словаре только для сортировки ключей.
Метод принимает любой словарь в качестве аргумента и возвращает отсортированные ключи этого словаря.
Рассмотрим на примере. Объявим словарь с именем dictvar . Затем используем метод sorted() для сортировки его ключей и сохраним в переменной с именем sorted_key . Выведем значения этой переменной на экран.
В результате запуска этого кода получим список отсортированных по возрастанию ключей.
Метод clear()
И финальный метод из нашей подборки топ-10 методов словарей в Python. Данный метод используется, чтобы убрать все элементы из словаря, очистить его.
clear() не принимает никакие аргументы и возвращает пустой словарь.
Как и в предыдущем примере, объявим словарь с именем dictvar . Затем применим к нему метод clear() . Для наглядности выведем на экран содержимое словаря до и после применения метода clear() .
Мы получили пустой словарь.
Заключение
В этой статье мы рассказали про топ-10 методов словарей в Python и показали их работу на простых примерах. Надеемся, это поможет вам более эффективно работать со словарями.
Английский для программистов
Наш телеграм канал с тестами по английскому языку для программистов. Английский это часть карьеры программиста. Поэтому полезно заняться им уже сейчас
Калькулятор объема цилиндра
Рассчитайте онлайн объем любого цилиндрического объекта: трубы, бочки, банки.
Что известно
Размерность
Радиус основания
см
Диаметр основания
см
Площадь основания
см2
Высота
см
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🛢️ Когда требуется знать объем цилиндра?
Знание объема цилиндра может потребоваться в различных ситуациях, к примеру:
- Расчет объема бака или резервуара: если вы планируете хранить жидкость или газ в баке или резервуаре, то может быть важно знать его объем, чтобы знать, сколько материала вы можете в него поместить.
- Расчет объема емкости для транспортировки: если вы занимаетесь перевозкой жидкостей или газов, то может потребоваться знать объем емкости, чтобы убедиться, что вы можете перевезти нужное количество материала.
- Расчет объема цилиндрических труб: если вы занимаетесь установкой трубопроводов или работой с другими цилиндрическими объектами, то может быть полезно знать их объем, чтобы правильно рассчитать количество материала, необходимого для работы.
- Расчет объема бутылки или бочки: если вы хотите знать, сколько жидкости вы можете вместить в определенную бутылку или бочку, то калькулятор объема цилиндра может помочь рассчитать объем емкости.
- Определение объема цилиндрических объектов, используемых в декоративных целях, например, колонн, скульптур и других элементов архитектуры и дизайна.
Также умение рассчитывать объем цилиндра пригодится в строительстве, химии и фармацевтике, механике и технике, производстве, учебе и творчестве.
📏 Как рассчитывается объем цилиндра?
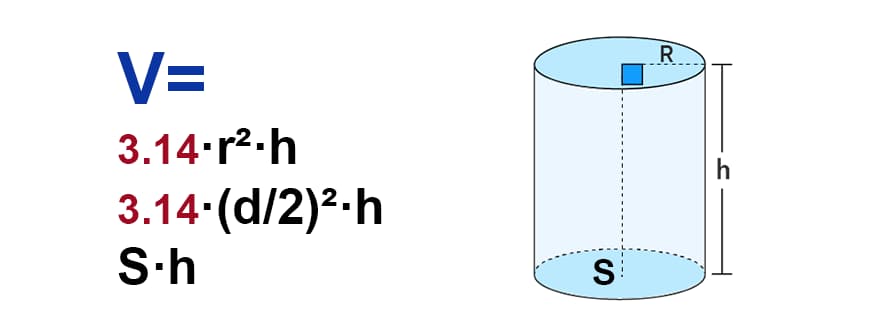
Объем цилиндра можно рассчитать по формуле:
V = πr²h
где V – объем цилиндра, r – радиус основания цилиндра, h – высота цилиндра, π (пи) – математическая константа, приблизительно равная 3,14.
Чтобы использовать эту формулу, необходимо знать значения радиуса основания и высоты цилиндра. Радиус основания – это расстояние от центра основания до края, высота цилиндра – это расстояние между основаниями цилиндра.
Например, если радиус основания цилиндра равен 5 см, а высота цилиндра составляет 10 см, то объем цилиндра можно рассчитать следующим образом:
V = 3,14 x 5² x 10 = 785 см3
Обратите внимание, что единицы измерения должны быть одинаковыми, чтобы получить правильный ответ. Если радиус основания и высота цилиндра измеряются в сантиметрах, то и объем цилиндра должен быть выражен в кубических сантиметрах.
🧮 Что такое калькулятор объема цилиндра?
Калькулятор объема цилиндра – это инструмент, который позволяет автоматически рассчитывать объем цилиндра по его размерам. Обычно калькулятор объема цилиндра предоставляет пользователю простую форму, где нужно ввести значение радиуса основания и высоты цилиндра, а затем нажать кнопку «Рассчитать». Калькулятор объема цилиндра может быть представлен в виде программы на компьютере или мобильном устройстве, а также в виде онлайн-сервиса на веб-сайте, как у нас.
Использование калькулятора объема цилиндра упрощает и ускоряет процесс расчета объема цилиндра, особенно если нужно рассчитать объем нескольких цилиндров или если значения радиуса и высоты цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, включая науку, технику, строительство, производство, учебу и домашнее хозяйство.
📏 Как работает калькулятор объема цилиндра?
Калькулятор объема цилиндра работает на основе математической формулы для расчета объема цилиндра, рассмотренной выше.
Чтобы рассчитать объем цилиндра, пользователь должен ввести значения радиуса основания и высоты цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и выводит результат в соответствующем поле на экране.
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.
🛢 Как использовать калькулятор объема цилиндра?
Для использования калькулятора объема цилиндра следуйте этим простым шагам:
- Откройте калькулятор объема цилиндра, который находится на компьютере, мобильном устройстве или на веб-сайте.
- Введите значение радиуса основания цилиндра в соответствующее поле калькулятора. Если вы используете калькулятор, который принимает во внимание диаметр, убедитесь, что вы выбрали правильную единицу измерения.
- Введите значение высоты цилиндра в соответствующее поле калькулятора. Убедитесь, что вы выбрали правильную единицу измерения.
- Нажмите кнопку «Рассчитать» или «Получить результат». Калькулятор выполнит расчеты и выведет объем цилиндра в соответствующем поле.
- Проверьте результаты и убедитесь, что все значения введены правильно и выбраны правильные единицы измерения.
- Если нужно рассчитать объем нескольких цилиндров, повторите шаги 2-5 для каждого цилиндра.
- Сохраните результаты или скопируйте их в буфер обмена, если нужно использовать их в другой программе или приложении.
В зависимости от функционала калькулятор может иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
В чем измеряется объем цилиндра?
Объем цилиндра измеряется в кубических единицах длины. Например, если размеры цилиндра измеряются в метрах, то его объем будет выражаться в кубических метрах (м³). Если размеры измеряются в сантиметрах, то объем будет выражаться в кубических сантиметрах (см³). Также можно использовать другие единицы измерения, такие как литры или галлоны, которые также выражают объем жидкости или газа, но они не являются кубическими единицами длины.
Несколько лайфхаков
Если вы хотите упростить расчет объема цилиндра, есть несколько лайфхаков, которые могут пригодиться:
- Используйте формулу площади основания цилиндра. Объем цилиндра можно вычислить, умножив площадь основания на высоту. Если вы знаете формулу площади основания цилиндра, то можете сначала вычислить ее, а затем умножить на высоту, чтобы найти объем.
- Используйте приближенное значение числа Пи. Число Пи является бесконечной десятичной дробью, но для большинства расчетов достаточно использовать его приближенное значение. Например, можно использовать значение 3,14 или 22/7 вместо точного значения числа Пи, которое равно примерно 3,14159265359.
- Используйте онлайн калькулятор. Наш онлайн калькулятор объема цилиндра поможет быстро выполнить расчеты за вас. Просто введите значения радиуса и высоты, и калькулятор автоматически вычислит объем.
- Используйте замены единиц измерения. Если вы хотите перевести объем из одной единицы измерения в другую, например, из кубических сантиметров в литры, можете также воспользоваться калькулятором на нашем сайте.
❓ Вопросы и ответы
Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.
Что такое цилиндр?
Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.
Как вычислить объем цилиндра?
Объем цилиндра можно вычислить, используя формулу:
V = πr²h
где V – объем цилиндра, π – число Пи (приблизительно равно 3.14), r – радиус основания цилиндра и h – высота цилиндра.
Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?
Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.
Как найти радиус или диаметр цилиндра, если они неизвестны?
Если известна площадь основания цилиндра, можно найти радиус, используя формулу:
r = √(A/π)
где A – площадь основания цилиндра.
Если известен объем цилиндра, можно найти радиус, используя формулу:
r = √(V/πh)
где V – объем цилиндра, h – высота цилиндра.
Диаметр можно найти, удваивая радиус.
Как найти объем трубы или канала?
Для трубы или канала формула для вычисления объема имеет немного другой вид:
V = πr²h
где V – объем, r – радиус, h – длина (высота) трубы или канала.
Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:
V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.
Как узнать, сколько литров вмещает бочка?
Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота – 1,5 метра, то ее объем будет:
V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.
Как узнать, сколько литров вмещает труба?
Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы – 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:
V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.
Какой тип калькулятора нужен для расчета объема цилиндра?
Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.
Какие значения нужно ввести в калькулятор объема цилиндра?
Для расчета объема цилиндра необходимо ввести значение радиуса основания цилиндра и высоты цилиндра.
Какие единицы измерения могут использоваться при вводе значений в калькулятор объема цилиндра?
Единицы измерения, которые могут использоваться при вводе значений в калькулятор объема цилиндра, это сантиметры, метры, дюймы и т.д.
Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
Где можно найти калькулятор объема цилиндра?
Калькулятор объема цилиндра можно найти в Интернете на специализированных сайтах, в приложениях для мобильных устройств и на компьютерах, а также в других программных приложениях, связанных с инженерными и научными расчетами.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Посчитать объём коробки
- Главная
- /
- Логистика
- /
- Посчитать объём коробки
Чтобы посчитать объем коробки или нескольких коробок воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
Расчет объема коробки
Длина коробки
Ширина коробки
Высота коробки
Объем коробки:
0
Просто введите длину, ширину и высоту коробки и узнаете её объём.
Расчет объема нескольких коробок
Количество коробок
шт
Длина коробки
Ширина коробки
Высота коробки
Объем одной коробки:
0
Общий объем всех коробок:
0
Теория
Коробка это прямоугольный параллелепипед, который имеет длину A, ширину B и высоту (глубину) C. Её объём считается по следующей формуле:
Формула
V = A⋅B⋅C
Пример
К примеру, возьмём коробку, у которой ширина равна 56 см, высота – 40 см, глубина – 32 см и посчитаем её объём:
V = 56⋅40⋅32 = 71680 см³
Если нам необходимо знать объём в кубометрах, нужно полученную цифру разделить на 1 000 000:
V = 71680/1000000 = 0.07168 ≈ 0.07 м³
См. также
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример – объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a – длина, b – ширина, c – высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще – достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³. Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед – фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула. Galina7v7 7 лет назад Если ваш вопрос трактовать так: “как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах. Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона – 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3 Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно – длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических. moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать. vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы – это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3. EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |
Загрузить PDF
Загрузить PDF
Объем фигуры представляет собой занимаемое этой фигурой трехмерное пространство.[1]
Представьте себе объем как количество жидкости (или воздуха, или песка), которым можно заполнить данную фигуру. Объем измеряется в кубических единицах (мм3, см3, м3).[2]
Эта статья расскажет вам, как вычислять объем шести трехмерных фигур. Вы можете заметить, что многие формулы для вычисления объема схожи, что упрощает их запоминание.
-
1
Куб – это трехмерная фигура, которая имеет шесть одинаковых квадратных граней, то есть все ее стороны (ребра) равны.[3]
- Например, игральная кость – это куб.
-
2
Формула нахождения объема куба: V = s3, где V – объем, а s – длина ребра.
- Возведение в куб аналогично следующему умножению: s3 = s * s * s
-
3
Найдите длину стороны (ребра) куба. Она будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой). Так как ребра куба равны, измеряйте любое ребро.
- Если вы не уверены, что ваша фигура является кубом, измерьте каждую сторону, чтобы убедиться, что они равны. Если они не равны, перейдите к следующему разделу.
-
4
Подставьте длину ребра куба в формулу V = s3. Например, если ребро куба равно 5 см, напишите формулу следующим образом: V = 53 = 5 * 5 * 5 = 125 см3 – это объем куба.
-
5
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребро куба измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах. Если, например, сторона куба равна 3 см, то V = 33 = 27см3.
Реклама
-
1
Прямоугольный параллелепипед или прямоугольная призма – это трехмерная фигура с шестью гранями, каждая из которых является прямоугольником (вспомните коробку из под обуви). [4]
- Куб – это частный случай прямоугольного параллелепипеда, у которого все ребра равны.
-
2
Формула нахождения объема прямоугольного параллелепипеда или прямоугольной призмы: V = l*w*h, где V = объем, l = длина, w = ширина, h = высота.[5]
-
3
Длина прямоугольного параллелепипеда – это самое длинное ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Длина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: длина прямоугольного параллелепипеда равна 4 см, то есть l = 4 см.
- Не беспокойтесь о том, какие ребра выбрать в качестве длины, ширины и высоты. В любом случае в итоге вы получите правильный ответ (только измерьте три ребра, перпендикулярные друг другу).
-
4
Ширина прямоугольного параллелепипеда – это самое короткое ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Ширина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: ширина прямоугольного параллелепипеда равна 3 см, то есть w = 3 см.
- Если вы измеряете ребра параллелепипеда линейкой или рулеткой, не забудьте измерить их в одинаковых единицах измерения. Не измеряйте одно ребро в миллиметрах, а другое в сантиметрах.
-
5
Высота прямоугольного параллелепипеда – это расстояние между его нижней и верхней гранями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: высота прямоугольного параллелепипеда равна 6 см, то есть h = 6 см.
-
6
Подставьте найденные значения в формулу V = l*w*h.
- В нашем примере l = 4, w = 3 и h = 6. Поэтому V = 4*3*6 = 72.
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребра измерялись в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 72 см3.
- Если в прямоугольной призме l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см3
Реклама
-
1
Цилиндр – это трехмерная фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.[6]
- Например, банка или батарейка АА имеют форму цилиндра.
-
2
Формула нахождения объема цилиндра: V = πr2h, где V – объем, h – высота, r – радиус основания и πr2 – площадь основания цилиндра.
- В некоторых задачах ответ требуется представить с пи, а в некоторых вместо пи подставить 3,14.
- Формула для нахождения объема цилиндра на самом деле очень похожа на формулу вычисления объема прямоугольной призмы, то есть вы перемножаете высоту и площадь основания. В прямоугольной призме площадь основания равна l*w, а в цилиндре она равна πr2.
-
3
Найдите радиус основания. Он, скорее всего, дан в задаче. Если дан диаметр, разделите его на 2, чтобы найти радиус (d = 2r).
-
4
Если радиус не дан, измерьте его. Для этого измерьте основание цилиндра при помощи линейки или рулетки. Измеряйте основание в его самой широкой части (то есть измерьте диаметр основания), а затем разделите полученное значение на 2, чтобы найти радиус.
- Другой вариант – измерьте длину окружности цилиндра (то есть измерьте обхват цилиндра) при помощи рулетки, а затем найдите радиус по формуле r = с/2π, где с – обхват (длина окружности) цилиндра (2π = 6,28).
- Например, если обхват цилиндра равен 8 см, то радиус будет равен 1,27 см.
- Если вам нужно точное измерение, вы можете использовать оба метода, чтобы убедиться, что значения радиуса совпадают (нахождение радиуса через длину окружности является более точным методом).
-
5
Вычислите площадь круглого основания. Для этого подставьте радиус в формулу πr2.
- Если радиус основания равен 4 см, то площадь основания равна π42.
- 42 = 4 * 4 = 16. 16*π = 16*3,14 = 50,24 см2
- Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус.
-
6
Найдите высоту цилиндра. Это расстояние между двумя круглыми основаниями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
-
7
Умножьте площадь основания на высоту цилиндра, чтобы найти его объем. Или же просто подставьте значения соответствующих величин в формулу V = πr2h. В нашем примере, когда радиус основания равен 4 см, а высота равна 10 см:
- V = π4210
- π42 = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 502,4 см3.
Реклама
-
1
Пирамида – это трехмерная фигура, в основании которой лежит многоугольник, а грани являются треугольниками, имеющими общую вершину. [7]
Правильная пирамида – это трехмерная фигура, в основании которой лежит правильный многоугольник (с равными сторонами), а вершина проецируется в центр основания.[8]
- Обычно мы представляем пирамиду, имеющую квадратное основание, но в основании пирамиды может лежать многоугольник с 5, 6 или даже со 100 сторонами!
- Пирамида с круглым основанием называется конусом, который будет обсуждаться в следующем разделе.
-
2
Формула нахождения объема правильной пирамиды: V = 1/3bh, где b – площадь основания пирамиды, h – высота пирамиды (перпендикуляр, соединяющий основание и вершину пирамиды).
- Эта формула для вычисления объема пирамиды одинаково годна как для правильных пирамид (в которых вершина проецируется в центр основания), так и для наклонных (в которых вершина не проецируется в центр основания).
-
3
Вычислите площадь основания. Формула будет зависеть от фигуры, лежащей в основании пирамиды. В нашем примере в основании пирамиды лежит квадрат со стороной 6 см. Площадь квадрата равна s2, где s – сторона квадрата. Таким образом, в нашем примере площадь основания пирамиды равна 62 = 36 см2
- Площадь треугольника равна 1/2bh, где h – высота треугольника, b – сторона, к которой проведена высота.
- Площадь любого правильного многоугольника можно вычислить по формуле: А = 1/2ра, где А – площадь, р – периметр фигуры, а – апофема (отрезок, соединяющий центр фигуры с серединой любой стороны фигуры). Для получения дополнительной информации о нахождении площади многоугольников прочитайте эту статью.[9]
-
4
Найдите высоту пирамиды. Высота будет дана в задаче. В нашем примере высота пирамиды равна 10 см.
-
5
Умножьте площадь основания пирамиды на ее высоту, а затем разделите полученный результат на 3, чтобы найти объем пирамиды. Формула для вычисления объема пирамиды: V = 1/3bh. В нашем примере площадь основания равна 36, а высота равна 10, поэтому объем: 36*10*1/3 = 120.
- Если, например, дана пирамида с пятиугольным основанием площадью 26, а высота пирамиды равна 8, то объем пирамиды: 1/3*26*8 = 69,33.
-
6
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 120 см3.
Реклама
-
1
Конус – это трехмерная фигура, которая имеет круглое основание и одну вершину. Или конус – это особый случай пирамиды с круглым основанием.[10]
- Если вершина конуса находится непосредственно над центром круглого основания, то конус называется прямым; в противном случае конус называется наклонным. Но формула для вычисления объема конуса одинаковая для обоих типов конуса.
-
2
Формула для вычисления объема конуса: V = 1/3πr2h, где r – радиус круглого основания, h – высота конуса.
- b = πr2 – это площадь круглого основания конуса. Таким образом, формулу для вычисления объема конуса можно записать так: V = 1/3bh, что совпадает с формулой нахождения объема пирамиды!
-
3
Вычислите площадь круглого основания. Радиус должен быть дан в задаче. Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Для вычисления площади круглого основания подставьте радиус в формулу πr2.
- Например, радиус круглого основания конуса равен 3 см. Тогда площадь этого основания равна π32.
- π32 = π(3*3) = 9π.
- = 28,27 см2
-
4
Найдите высоту конуса. Это перпендикуляр, опущенный из вершины к основанию пирамиды. В нашем примере высота конуса равна 5 см.
-
5
Перемножьте высоту конуса и площадь основания. В нашем примере площадь основания равна 28,27 см2, а высота равна 5 см, поэтому bh = 28,27 * 5 = 141,35.
-
6
Теперь умножьте полученный результат на 1/3 (или просто разделите его на 3), чтобы найти объем конуса. В описанном выше шаге вы нашли объем цилиндра, а объем конуса всегда в 3 раза меньше объема цилиндра.
- В нашем примере: 141,35 * 1/3 = 47,12 – это объем конуса.
- Или: 1/3π325 = 47,12
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 47,12 см3.
Реклама
-
1
Шар – это идеально круглая трехмерная фигура, каждая точка поверхности которой равноудалена от одной точки (центра шара). [11]
-
2
Формула для вычисления объема шара: V = 4/3πr3, где r – радиус шара.[12]
-
3
Найдите радиус шара. Радиус должен быть дан в задаче. Если дан диаметр шара, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Например, радиус шара равен 3 см.
-
4
Если радиус не дан, вычислите его. Для этого измерьте длину окружности шара (например, теннисного мяча) в его самой широкой части при помощи веревки, нити или другого подобного предмета. Затем измерьте длину веревки, чтобы найти длину окружности. Разделите полученное значение на 2π (или на 6,28), чтобы вычислить радиус шара.
- Например, если вы измерили мяч и нашли, что длина его окружности равна 18 см, разделите это число на 6,28 и получите, что радиус мяча равен 2,87 см.
- Проделайте 3 измерения окружности шара, а затем усредните полученные значения (для этого сложите их и сумму разделите на 3), чтобы убедиться, что вы получили значение, близкое к истинному.
- Например, в результате трех измерений длины окружности вы получили следующие результаты: 18 см, 17,75 см, 18,2 см. Сложите эти значения: 18 + 17,5 + 18,2 = 53,95, а затем разделите их на 3: 53,95/3 = 17,98. Используйте это среднее значение в расчетах объема шара.
-
5
Возведите радиус в куб (r3). То есть r3 = r*r*r. В нашем примере r = 3, поэтому r3 = 3 * 3 * 3 = 27.
-
6
Теперь умножьте полученный результат на 4/3. Вы можете использовать калькулятор или выполнить умножение вручную, а затем упростить дробь. В нашем примере: 27*4/3 = 108/3 = 36.
-
7
Умножьте полученный результат на π (3,14), чтобы найти объем шара.
- В нашем примере: 36*3,14 = 113,09.
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 113,09 см3.
Реклама
Об этой статье
Эту страницу просматривали 74 580 раз.