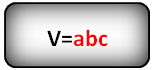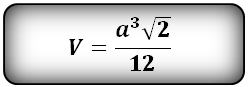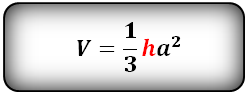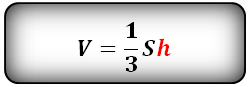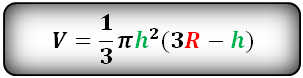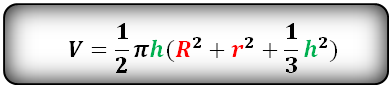Как найти объем колена - Сайт, где вы сможете решить свои вопросы

a – сторона куба

Формула объема куба, (V):

a, b, c – стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

R – радиус шара

π ≈ 3.14

По формуле, если дан радиус, можно найти объема шара, (V):

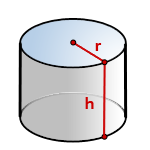
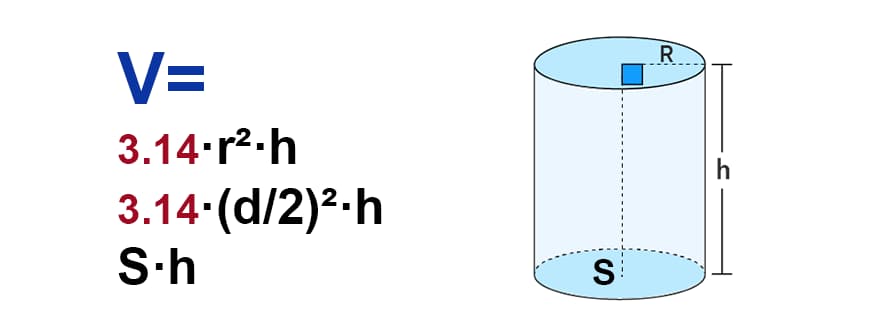
h – высота цилиндра

r – радиус основания

π ≈ 3.14

По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

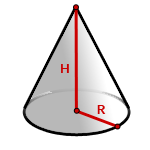
R – радиус основания

H – высота конуса

π ≈ 3.14

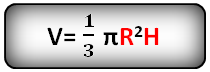
Формула объема конуса, если известны радиус и высота (V):

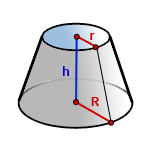
r – радиус верхнего основания

R – радиус нижнего основания

h – высота конуса

π ≈ 3.14

Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

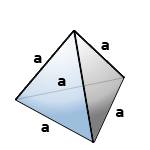
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.

а – ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

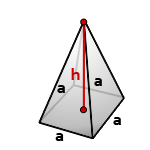
a – сторона основания

h – высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

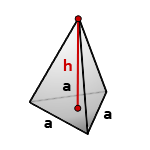
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

a – сторона основания

h – высота пирамиды

Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

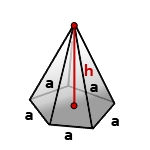
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h – высота пирамиды

a – сторона основания пирамиды

n – количество сторон многоугольника в основании

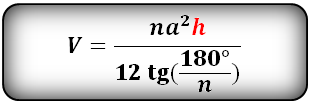
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

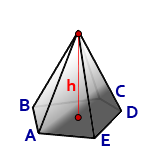
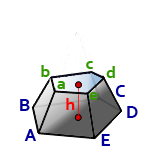
h – высота пирамиды

S – площадь основания ABCDE

Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):

h – высота пирамиды

S_ниж – площадь нижнего основания, ABCDE

S_верх – площадь верхнего основания, abcde

Формула объема усеченной пирамиды, (V):

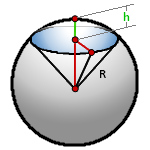
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара

h – высота сегмента

π ≈ 3.14

Формула для расчета объема шарового сегмента, (V):

R – радиус шара

h – высота сегмента

π ≈ 3.14

Формула объема шарового сектора, (V):

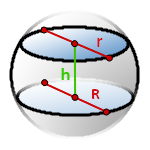
h – высота шарового слоя

R – радиус нижнего основания

r – радиус верхнего основания

π ≈ 3.14

Формула объема шарового слоя, (V):

Источник

Калькулятор объема цилиндра

Рассчитайте онлайн объем любого цилиндрического объекта: трубы, бочки, банки.

Что известно

Размерность

Радиус основания

см

Диаметр основания

см

Площадь основания

см²

Высота

см

Раcсчитать

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

🛢️ Когда требуется знать объем цилиндра?

Знание объема цилиндра может потребоваться в различных ситуациях, к примеру:

Расчет объема бака или резервуара: если вы планируете хранить жидкость или газ в баке или резервуаре, то может быть важно знать его объем, чтобы знать, сколько материала вы можете в него поместить.
Расчет объема емкости для транспортировки: если вы занимаетесь перевозкой жидкостей или газов, то может потребоваться знать объем емкости, чтобы убедиться, что вы можете перевезти нужное количество материала.
Расчет объема цилиндрических труб: если вы занимаетесь установкой трубопроводов или работой с другими цилиндрическими объектами, то может быть полезно знать их объем, чтобы правильно рассчитать количество материала, необходимого для работы.
Расчет объема бутылки или бочки: если вы хотите знать, сколько жидкости вы можете вместить в определенную бутылку или бочку, то калькулятор объема цилиндра может помочь рассчитать объем емкости.
Определение объема цилиндрических объектов, используемых в декоративных целях, например, колонн, скульптур и других элементов архитектуры и дизайна.

Также умение рассчитывать объем цилиндра пригодится в строительстве, химии и фармацевтике, механике и технике, производстве, учебе и творчестве.

📏 Как рассчитывается объем цилиндра?

Объем цилиндра можно рассчитать по формуле:

V = πr²h

где V – объем цилиндра, r – радиус основания цилиндра, h – высота цилиндра, π (пи) – математическая константа, приблизительно равная 3,14.

Чтобы использовать эту формулу, необходимо знать значения радиуса основания и высоты цилиндра. Радиус основания – это расстояние от центра основания до края, высота цилиндра – это расстояние между основаниями цилиндра.

Например, если радиус основания цилиндра равен 5 см, а высота цилиндра составляет 10 см, то объем цилиндра можно рассчитать следующим образом:

V = 3,14 x 5² x 10 = 785 см³

Обратите внимание, что единицы измерения должны быть одинаковыми, чтобы получить правильный ответ. Если радиус основания и высота цилиндра измеряются в сантиметрах, то и объем цилиндра должен быть выражен в кубических сантиметрах.

🧮 Что такое калькулятор объема цилиндра?

Калькулятор объема цилиндра – это инструмент, который позволяет автоматически рассчитывать объем цилиндра по его размерам. Обычно калькулятор объема цилиндра предоставляет пользователю простую форму, где нужно ввести значение радиуса основания и высоты цилиндра, а затем нажать кнопку «Рассчитать». Калькулятор объема цилиндра может быть представлен в виде программы на компьютере или мобильном устройстве, а также в виде онлайн-сервиса на веб-сайте, как у нас.

Использование калькулятора объема цилиндра упрощает и ускоряет процесс расчета объема цилиндра, особенно если нужно рассчитать объем нескольких цилиндров или если значения радиуса и высоты цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, включая науку, технику, строительство, производство, учебу и домашнее хозяйство.

📏 Как работает калькулятор объема цилиндра?

Калькулятор объема цилиндра работает на основе математической формулы для расчета объема цилиндра, рассмотренной выше.

Чтобы рассчитать объем цилиндра, пользователь должен ввести значения радиуса основания и высоты цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и выводит результат в соответствующем поле на экране.

Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.

🛢 Как использовать калькулятор объема цилиндра?

Для использования калькулятора объема цилиндра следуйте этим простым шагам:

Откройте калькулятор объема цилиндра, который находится на компьютере, мобильном устройстве или на веб-сайте.
Введите значение радиуса основания цилиндра в соответствующее поле калькулятора. Если вы используете калькулятор, который принимает во внимание диаметр, убедитесь, что вы выбрали правильную единицу измерения.
Введите значение высоты цилиндра в соответствующее поле калькулятора. Убедитесь, что вы выбрали правильную единицу измерения.
Нажмите кнопку «Рассчитать» или «Получить результат». Калькулятор выполнит расчеты и выведет объем цилиндра в соответствующем поле.
Проверьте результаты и убедитесь, что все значения введены правильно и выбраны правильные единицы измерения.
Если нужно рассчитать объем нескольких цилиндров, повторите шаги 2-5 для каждого цилиндра.
Сохраните результаты или скопируйте их в буфер обмена, если нужно использовать их в другой программе или приложении.

В зависимости от функционала калькулятор может иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.

В чем измеряется объем цилиндра?

Объем цилиндра измеряется в кубических единицах длины. Например, если размеры цилиндра измеряются в метрах, то его объем будет выражаться в кубических метрах (м³). Если размеры измеряются в сантиметрах, то объем будет выражаться в кубических сантиметрах (см³). Также можно использовать другие единицы измерения, такие как литры или галлоны, которые также выражают объем жидкости или газа, но они не являются кубическими единицами длины.

Несколько лайфхаков

Если вы хотите упростить расчет объема цилиндра, есть несколько лайфхаков, которые могут пригодиться:

Используйте формулу площади основания цилиндра. Объем цилиндра можно вычислить, умножив площадь основания на высоту. Если вы знаете формулу площади основания цилиндра, то можете сначала вычислить ее, а затем умножить на высоту, чтобы найти объем.
Используйте приближенное значение числа Пи. Число Пи является бесконечной десятичной дробью, но для большинства расчетов достаточно использовать его приближенное значение. Например, можно использовать значение 3,14 или 22/7 вместо точного значения числа Пи, которое равно примерно 3,14159265359.
Используйте онлайн калькулятор. Наш онлайн калькулятор объема цилиндра поможет быстро выполнить расчеты за вас. Просто введите значения радиуса и высоты, и калькулятор автоматически вычислит объем.
Используйте замены единиц измерения. Если вы хотите перевести объем из одной единицы измерения в другую, например, из кубических сантиметров в литры, можете также воспользоваться калькулятором на нашем сайте.

❓ Вопросы и ответы

Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.

Что такое цилиндр?

Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.

Как вычислить объем цилиндра?

Объем цилиндра можно вычислить, используя формулу:

V = πr²h

где V – объем цилиндра, π – число Пи (приблизительно равно 3.14), r – радиус основания цилиндра и h – высота цилиндра.

Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?

Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.

Как найти радиус или диаметр цилиндра, если они неизвестны?

Если известна площадь основания цилиндра, можно найти радиус, используя формулу:

r = √(A/π)

где A – площадь основания цилиндра.

Если известен объем цилиндра, можно найти радиус, используя формулу:

r = √(V/πh)

где V – объем цилиндра, h – высота цилиндра.

Диаметр можно найти, удваивая радиус.

Как найти объем трубы или канала?

Для трубы или канала формула для вычисления объема имеет немного другой вид:

V = πr²h

где V – объем, r – радиус, h – длина (высота) трубы или канала.

Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:

V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.

Как узнать, сколько литров вмещает бочка?

Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота – 1,5 метра, то ее объем будет:

V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.

Как узнать, сколько литров вмещает труба?

Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы – 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:

V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.

Какой тип калькулятора нужен для расчета объема цилиндра?

Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.

Какие значения нужно ввести в калькулятор объема цилиндра?

Для расчета объема цилиндра необходимо ввести значение радиуса основания цилиндра и высоты цилиндра.

Какие единицы измерения могут использоваться при вводе значений в калькулятор объема цилиндра?

Единицы измерения, которые могут использоваться при вводе значений в калькулятор объема цилиндра, это сантиметры, метры, дюймы и т.д.

Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?

Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.

Где можно найти калькулятор объема цилиндра?

Калькулятор объема цилиндра можно найти в Интернете на специализированных сайтах, в приложениях для мобильных устройств и на компьютерах, а также в других программных приложениях, связанных с инженерными и научными расчетами.

Расчет объема треугольника

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

Формула расчета объема треугольника:

V – объем треугольника;
S – площадь треугольника;
h – толщина треугольника.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета объема треугольника. С помощью этого онлайн калькулятора расчета объема треугольника вы сможете вычислить объем треугольника по площади и толщине.

Все формулы объемов геометрических тел

1. Расчет объема куба

a – сторона куба

Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a , b , c – стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

3. Формула для вычисления объема шара, сферы

R – радиус шара

По формуле, если дан радиус, можно найти объема шара, (V):

4. Как вычислить объем цилиндра ?

h – высота цилиндра

r – радиус основания

По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

5. Как найти объем конуса ?

R – радиус основания

H – высота конуса

Формула объема конуса, если известны радиус и высота (V):

7. Формула объема усеченного конуса

r – радиус верхнего основания

R – радиус нижнего основания

h – высота конуса

8. Объем правильного тетраэдра

Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.

а – ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

9. Объем правильной четырехугольной пирамиды

a – сторона основания

h – высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

10. Объем правильной треугольной пирамиды

a – сторона основания

h – высота пирамиды

Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

11. Найти объем правильной пирамиды

h – высота пирамиды

a – сторона основания пирамиды

n – количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

Объем геометрических фигур

Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

Размеры куба

[spoiler title=”источники:”]

http://www-formula.ru/2011-09-24-00-37-25

http://planetcalc.ru/131/

[/spoiler]

Источник

Калькуляторы объема от КАЛК.ПРО предоставляют возможность выполнить точный расчет кубатуры геометрических фигур и реальных предметов по базовым формулам тригонометрии, стереометрии, начертательной и Евклидовой геометрии. Инструменты будут полезны как в научной деятельности при определении объема цилиндра, пирамиды, конуса… так и в практической деятельности при необходимости рассчитать грузы, емкости, сооружения. Все расчеты сопровождаются подробным описанием алгоритма, формулами и примерами. Результаты предоставляются в условных единицах или в единицах СИ.

Единицы измерения объема (СИ)

1 мм³ (куб. миллиметр) = 0.000000001 м³;
1 см³ (куб. сантиметр) = 0.000001 м³;
1 дм³ (куб. дециметр / литр) = 0.001 м³;
1 км³ (куб. километр) = 1.000.000.000 м³.

Единицы измерения объема (внесистемные и имперские)

1 мл (миллилитр) = 0.001 л = 0.000001 м³;
1 л (литр) = 0.001 м³;
1 унция (англ.) = 28.413 мл = 0.028413 л = 0.000028413 м³;
1 унция (амер.) = 29.573 мл = 0.029573 л = 0.000029573 м³;
1 галлон (англ.) = 4.55 литра = 0.00455 м³;
1 галлон (амер.) = 3.785 литра = 0.00378541 м³;
1 дюйм³ = 0,0000163871 м³;
1 фут³ = 0.0283168 м³;
1 ярд³ = 0,76455 м³.

Для того чтобы начать расчет объема, выберите необходимый калькулятор:

Источник

Масса кольца, звена

Масса тела зависит от того, сколько это тело съело. Шутка. На самом деле нам надо его (тела) объем умножить на плотность материала, из которого оно сделано rho (см. таблицы плотностей):

Для вычисления объема кольца или круглого звена нужно площадь сечения проката или проволоки умножить на длину окружности кольца.
Площадь сечения различных профилей мы вычисляли в статье «Масса проволоки, прутка, проката». А длина окружности кольца вычисляется по одной из двух формул: или , где — внутренний диаметр кольца, — внешний диаметр кольца, — толщина проката или проволоки.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.