В сосуде, имеющем форму конуса, уровень жидкости достигает (displaystyle frac{3}{5}) высоты. Объём жидкости равен (108) мл. Найдите объём сосуда. Ответ дайте в миллилитрах.
Решение
Меньший конус подобен большему с коэффициентом (displaystyle frac{3}{5}). Объемы подобных тел относятся как куб коэффициента подобия. Значит, объем меньшего конуса с жидкостью в (displaystyle left(frac{3}{5}right)^3=frac{27}{125}) раза меньше объема большого конуса.
Значит, объем сосуда (большого конуса) равен (displaystyle V=frac{125}{27} cdot 108=500) мл.
Ответ: (500).
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 15) (Купить книгу)
как найти обьем налитой жидкости?
WAR
Знаток
(406),
на голосовании
7 лет назад
в сосуде имеющем форму конуса, уровень жидкости достигает 34 высоты, обьем сосуда равен 1680мл. чему равен обьем налитой жидкости?
Голосование за лучший ответ
Раиль Шарипов
Знаток
(428)
7 лет назад
Я принял, что сосуд находится основанием вниз.
Рассмотрим соотношение объема конического сосуда V к подобному ему конусу “воздуха” V2 – оно равно кубу коэффициента подобия их линейных величин, т. е.:
V/V2=(1/[1-3/4])^3, тогда
V2=V/(4^3)=1680/64=26,25 мл.
Объем искомого усеченого конуса налитой жидкости V1=V-V2=1680-26,25=1653,75 мл.
Костя Климов
Профи
(774)
6 лет назад
формула V= r^2pH* 1/3=1680
Новый обьем получается V=3/4r^2*3/4h*1/3 так как и радиус и высота стала 3/4 от начальной .
следовательно получается 9/16 r^2hp * 1/3, что в 9/16 раз больше изначального
Теперь домножаем на 9/16 1680 и получается 945 Вуаля
Pavel
Ученик
(222)
6 лет назад
В формуле объема коэффициент пропорциональности, относящийся к радиусу нового основания 3/4, должен возводиться в квадрат вместе с радиусом, т. е. V=1/3*3/4h*п (3/4r)^2, тогда общий коэффициент пропорциональности, показывающий во сколько раз новый объем меньше старого, равен не 9/16, а 27/64. В результате получаем 27/64*1680=708,75. Ответ 945 – ошибочный, он приведен в тренировочных заданиях базового уровня ЕГЭ 2016. В этом сборнике подобных ляпов в ответах многовато.
Online calculator to find the conical cylinder volume. This can be calculated by adding the volume of cylinder and cone. You will get the conical cylinder when the edge of the cylinder is cut off. The base of the cylinder is large circle and the top portion is smaller circle. The volume of a conical cylinder calculator would help you to find the total capacity that could be occupied inside the conical cylinder. Enter the radius, cylinder height and cone height to find the volume.
Online calculator to find the conical cylinder volume. This can be calculated by adding the volume of cylinder and cone. You will get the conical cylinder when the edge of the cylinder is cut off. The base of the cylinder is large circle and the top portion is smaller circle. The volume of a conical cylinder calculator would help you to find the total capacity that could be occupied inside the conical cylinder. Enter the radius, cylinder height and cone height to find the volume.
Code to add this calci to your website 
Formula:

Volume (V) = (π ×r × r × h) + ((1/3) × (π × r × r × c))
Where,
r = Radius
c = Cone Height
h =Cylinder Height
Example:
Calculate volume of conical cylinder having a radius of 5 cm,cone having height of 7 cm and cylinder having a height of 8 cm.
Solution:
V = (3.14 ×5 × 5 × 8) + ((1/3) × (3.14 × 5 × 5 × 7))
= 811.5781 cm3
Related Calculators:
- Right Cylinder Calc : Find A_L
- Sphere Calc : Find A
- Aquarium Glass Thickness Calculator
- Surface Area Of A Triangular Pyramid Calculator
- Lateral Surface Area Of Conical Cylinder Calculator
- How Many Months Since Calculator
Что такое вместимость сосуда
Вместимость сосуда — это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ — кубический метр, но в случае жидкости чаще используют литр.
Особенности расчета объема жидкости в сосуде
Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества — твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.
В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.
За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:
(h = frac{p}{rho times g}.)
(p) здесь — давление в паскалях, (rho) — плотность, (g) — ускорение свободного падения, константа.
Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.
При решении логических учебных задач на переливание жидкости из одного сосуда в другой может пригодиться понимание взаимосвязи объема жидкости и параметров сосуда. А для задач по физике часто требуется рассчитать объем, который занимает жидкость в сосуде, через ее массу. На практике это действительно один из самых удобных способов, не требующий ни специальных датчиков, ни сложных расчетов.
Задача
Найти объем керосина, зная массу одного и того же сосуда с ним, и без него. Масса пустого сосуда 440 грамм, полного — 600 грамм.
Решение:
Плотность керосина можно узнать из справочной таблицы — 800 (frac{кг}{м^{3}}.)
Вычислим массу керосина в сосуде: 600 – 440 = 160.
Подставим известные данные в формулу:
(V = frac{m}{rho} = frac{0,16}{800} = 0,0002 м^{3} = 200 см^{3}.)
Ответ: 200 (см^{3}.)
Как определить вместимость сосудов разных форм
Вычисление объема параллелепипеда
Параллелепипед — это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.
(V = S_{осн} times H. )
Прямоугольный параллелепипед — это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, — это куб.
Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:
(V = AB times AD times AA_{1} = abc.)
Объем куба равен кубу его стороны:
(V = a^{3}.)
Нахождение объема пирамиды
Пирамида — это многогранник, состоящий из основания — плоского многоугольника, вершины — точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды — это перпендикуляр, опущенный из вершины на плоскость основания.
(V = frac{1}{3} times S_{осн} times h.)
Чтобы определить объем усеченной пирамиды, надо знать площадь обоих оснований — (S_{1}) и (S_{2}).
(V = frac{1}{3} times h times (S_{1} + S_{2} + sqrt{S_{1} times S_{2}}). )
Как найти объем цилиндра
Цилиндр — это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
(R) — радиус основания цилиндра, (h) — его высота, равная образующей оси.
(V = S_{осн} times h = pi times R^{2} times h.)
Если нужно найти объем усеченного цилиндра, то понадобится не только R — радиус основания, но и наибольшая и наименьшая образующие. Они обозначаются буквой l — (l_{1}) и (l_{2}).
(V = pi times R^{2} times frac{l_{1} + l_{2}}{2}.)
Как высчитать объем конуса
Конус — это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.
(V = frac{1}{3} times S_{осн} times h = frac{1}{3} times pi times R^{2} times h.)
Чтобы найти объем усеченного конуса, понадобятся (R_{1}) и (R_{2}) — радиусы оснований, а также высота (h).
(V = frac{pi times h}{3} times (R_1^2 + R_2^2 + R_1 times R_2).)
Нахождение объема шара
Шар — это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.
(R) — радиус полукруга, равный радиусу шара.
(V = frac{4pi times R^{3}}{3}.)
Задание
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/3 высоты. Объем сосуда 540 мл. Чему равен объем налитой жидкости? Ответ дайте в миллиметрах.
Решение
- Объем конуса равен 1/3 произведения его высоты на площадь основания, а площадь основания — это площадь круга: V=1/3*h*Socн = 1/3*h*π*(D/2)2.
- Для решения данной задачи будем рассматривать объемы двух конусов:
- объем конуса, у которого уровень жидкости равен 1/3 высоты – V1/3,
- объем конуса, равный объему сосуда – Vсосуд
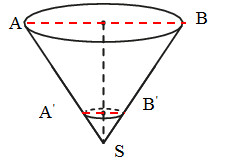
- Для удобства введем буквенные обозначения, как показано на рисунке, и рассмотрим треугольники АSВ и А‘SВ‘. Данные треугольники подобны. Из этого делаем вывод, что основание АВ больше основания А‘В‘ в 3 раза, так как высота треугольника АSВ в 3 раза больше высоты треугольника А‘SВ‘.
- АВ и А‘В‘ являются диаметрами оснований конусов.
- Запишем, чему равен объем большего конуса в буквенном виде:
Vсосуд = 1/3*h*π*(D/2)2
- Теперь запишем, чему равен объем меньшего конуса и преобразуем получившееся выражение:
V1/3 = 1/3*h/3*π*(D/2/3)2 = (1/3*h*π*(D/2)2)/(3*9) = Vсосуд / 27
- Осталось подставить объем сосуда в полученную формулу и найти объем налитой жидкости:
V1/3 = Vсосуд / 27 = 540 / 27 = 20 мл
Ответ: 20


