как найти объем конуса, если я знаю площадь осевого сечения?
Аня Алеева
Ученик
(125),
закрыт
8 лет назад
задача: осевым сечением служит равнобедренный прямоугольник, площадь которого 9 м? найти объем конуса
Дополнен 8 лет назад
треугольник а не прямоугольник
Лучший ответ
asa
Мудрец
(13083)
8 лет назад
Скорее всего в сечении равнобедренный прямоугольный тр-к, тогда H=R=3 м
V=ПR^2*H/3=9П куб. м
hugoИскусственный Интеллект (193131)
8 лет назад
на 3 забыл разделить
asa
Мудрец
(13083)
СПБ
Остальные ответы
Scarabey
Искусственный Интеллект
(110810)
8 лет назад
странная у вас фигура, равнобедренный ПРЯМОУГОЛЬНИК это вообще как???
Аня АлееваУченик (125)
8 лет назад
тоже думаю над этим вопросом
Аня АлееваУченик (125)
8 лет назад
видимо там треугольник
Scarabey
Искусственный Интеллект
(110810)
логично, а если точнее, этот гибрид вероятно равнобедренный прямоугольный треугольник, иначе решить не получится.
hugo
Искусственный Интеллект
(193131)
8 лет назад
ну так найди высоту и половину основания этого треугольника и подставь
они кстати равны будут
х*х/2=4,5
х^2=9
x=v9=3 это радиус и высота конуса
объём=1/3*Пи*3^2*3=9Пи м. куб
Похожие вопросы
Перед началом обращусь к вам с просьбой. Я пытаюсь помочь вам, а вы помогайте мне 🙂 Обязательно дочитывайте до конца, подписывайтесь на канал, задавайте свои вопросы по математике в комментарии или в соцсетях по ссылкам на канале. Помогайте мне продвинуть канал 🙂
Сейчас научимся решать задачи на объём конуса. Кстати, странно, что задачи заявлены на объём конуса, но представлены на площадь сечения. Но не будем спорить, им виднее.
Такие задачки решаются через коэффициент подобия. Находим, чему равен коэффициент подобия с помощью высот. Маленькая высота равна 1, большая 3, значит коэффициент равен 1/3. Как работать с коэффициентом подобия? Если сравниваем величины одномерные, то берём просто коэффициент подобия, если площади, то в квадрате, если объемы, то в кубе. В данном случае у нас площадь, значит 63 два раза умножаем на 1/3 и получаем 7. Значит площадь второго сечения равна 7.
Записывайтесь на семинар по базе ЕГЭ
Успейте записаться на интенсив ОГЭ
↓ ↓ ↓ ↓ ↓ За помощью обращайся сюда ↓ ↓ ↓ ↓ ↓
89174639366 (звонки, СМС) WA 89174639366 ВК Никита Тюрин
Задача 64135 Дано площадь осевого сечения конуса,…
Условие
![]()
Дано площадь осевого сечения конуса, найдите объем конуса
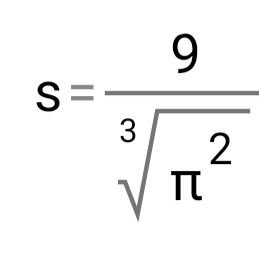
математика
212
Решение
![]()
★
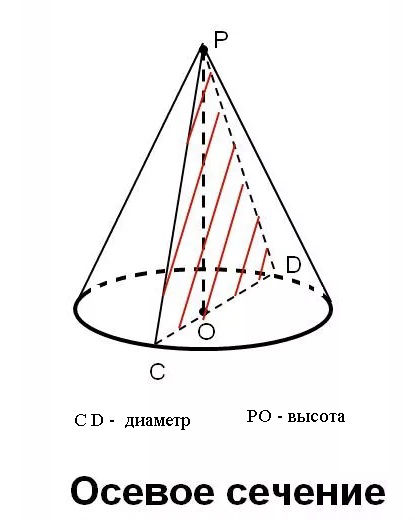
S_(осевого сечения)=(1/2)*2R*H
Осевое сечение равнобедренный прямоугольный треугольник ⇒ R=H
[m]frac{9}{sqrt[3]{π^2}}=cdot Rcdot H[/m] ⇒ [m]Rcdot H=frac{9}{sqrt[3]{π^2}}[/m][/m]
R=H
[m]Rcdot R=frac{9}{sqrt[3]{π^2}}[/m] ⇒ [m]R=sqrt{frac{9}{sqrt[3]{π^2}}}[/m]
[m]V=frac{1}{3}πR^2H=frac{1}{3}πcdot Rcdot RH=frac{1}{3}πcdot sqrt{frac{9}{sqrt[3]{π^2}}}cdot frac{9}{sqrt[3]{2π^2}}=[/m]
Написать комментарий
В данной публикации мы рассмотрим, каким образом можно посчитать объем прямого кругового конуса и разберем примеры решения задач.
-
Формула вычисления объема
- 1. Через площадь основания и высоту
- 2. Через радиус основания и высоту
- Примеры задач
Формула вычисления объема
1. Через площадь основания и высоту
Объем (V) конуса равняется одной третьей произведения его высоты на площадь основания:
![]()

2. Через радиус основания и высоту
Как мы знаем, основанием конуса является круг, площадь которого вычисляется по формуле: S = πR2.
Следовательно, формулу для вычисления объема конуса можно представить в виде:
![]()
Т.е. объем конуса равняется одной третьей произведения его высоты на число π и на радиус основания в квадрате.
Примечание: в расчетах значение числа π округляется до 3,14.
Формула для нахождения объема усеченного конуса представлена в отдельной публикации.
Примеры задач
Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см2, а также, высота – 9 см.
Решение:
Применим первую формулу, подставив в нее заданные значения:
![]()
Задание 2
Высота конуса равна 7 см, а его радиус – 3 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:![]()
Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.
Онлайн-калькулятор объема конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Формула объема прямого конуса
Объем прямого конуса можно рассчитать по следующей формуле:
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.
Рассмотрим несколько примеров.
Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.
Решение
l=5l=5
R=3R=3
Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:
l2=h2+R2l^2=h^2+R^2
Отсюда, hh:
h=l2−R2h=sqrt{l^2-R^2}
h=52−32h=sqrt{5^2-3^2}
h=25−9h=sqrt{25-9}
h=16h=sqrt{16}
h=4h=4
Затем находим площадь основания конуса. Это площадь круга радиуса RR:
Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26
Последние вычисления — нахождение объема конуса по формуле:
V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3
Ответ: 37.68 см3.37.68text{ см}^3.
Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.
Решение
D=8D=8
h=9h=9
Найдем радиус RR круга через его диаметр:
R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4
Площадь этого круга и есть основание нашего конуса:
Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24
Сам объем равен:
V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3
Ответ: 150.72 см3.150.72text{ см}^3.
Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!
