Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.
Онлайн-калькулятор объема конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
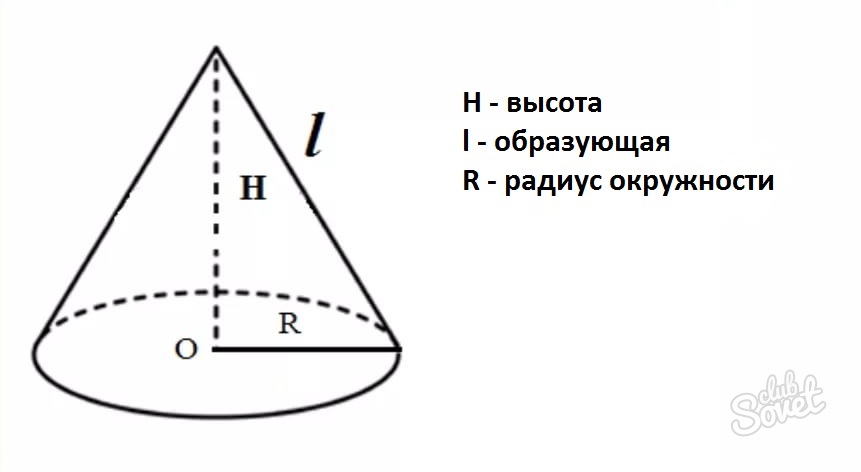
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
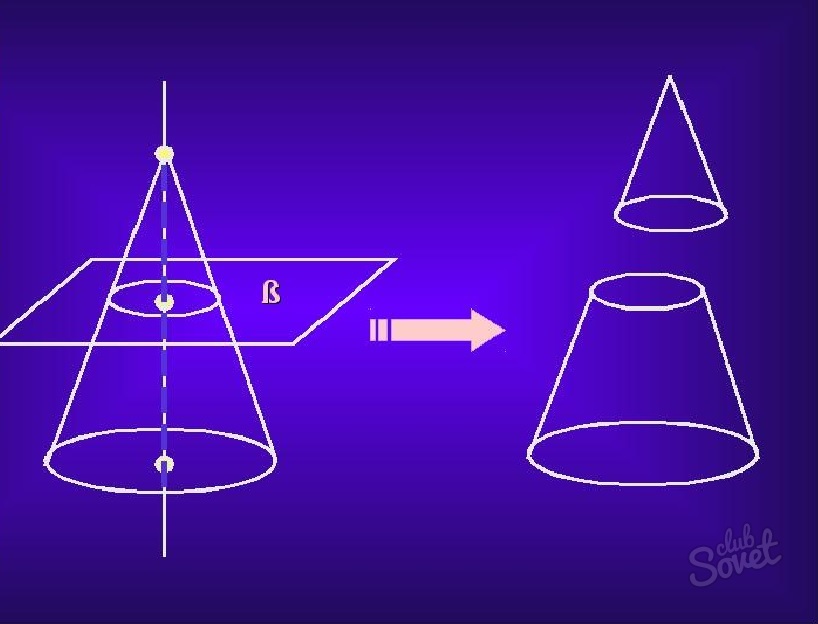
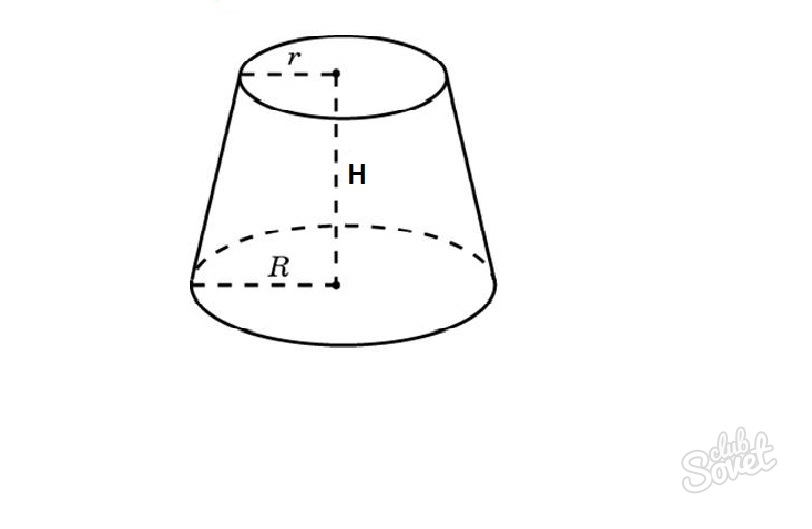
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
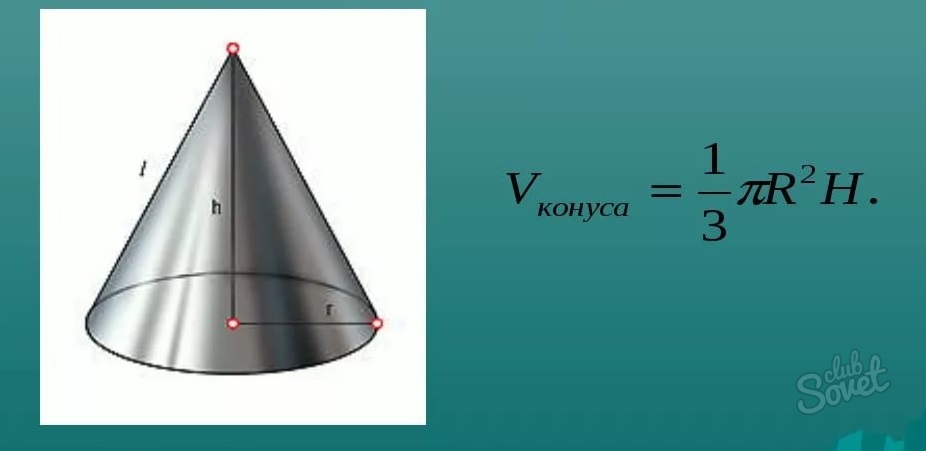
Формула объема прямого конуса
Объем прямого конуса можно рассчитать по следующей формуле:
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.
Рассмотрим несколько примеров.
Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.
Решение
l=5l=5
R=3R=3
Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:
l2=h2+R2l^2=h^2+R^2
Отсюда, hh:
h=l2−R2h=sqrt{l^2-R^2}
h=52−32h=sqrt{5^2-3^2}
h=25−9h=sqrt{25-9}
h=16h=sqrt{16}
h=4h=4
Затем находим площадь основания конуса. Это площадь круга радиуса RR:
Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26
Последние вычисления — нахождение объема конуса по формуле:
V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3
Ответ: 37.68 см3.37.68text{ см}^3.
Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.
Решение
D=8D=8
h=9h=9
Найдем радиус RR круга через его диаметр:
R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4
Площадь этого круга и есть основание нашего конуса:
Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24
Сам объем равен:
V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3
Ответ: 150.72 см3.150.72text{ см}^3.
Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!
Тест на тему “Объем конуса”
Объём конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём конуса
Для того чтобы посчитать объём конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Через площадь основания и высоту
Площадь основания Sосн =
Высота h =
V =
0
Округление ответа:
Через радиус и другие параметры
=
=
V =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Объём конуса через площадь основания и высоту
Чему равен объём конуса V, если площадь его основания Sосн, а высота h:
Формула
V = ⅓ ⋅ Sосн ⋅ h
Пример
Для примера посчитаем, чему равен объём конуса, у которого площадь основания Sосн = 3 см², а высота h = 5 см :
V = ⅓ ⋅ 3 ⋅ 5 = 15⁄3 = 5 см³
Объём конуса через образующую и радиус
Чему равен объём конуса V, если его образующая l, радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r² ⋅ √l² – r²
через диаметр:
V = ⅓ ⋅ π ⋅ (d/2)² ⋅ √l² – (d/2)²
Пример
Для примера посчитаем, чему равен объём конуса, у которого образующая l = 5 см, а радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2² ⋅ √5² – 2² = ⅓ ⋅ 12.56 ⋅ √21 ≈ 4.19 ⋅ 4.58 ≈ 19.19 см³
Объём конуса через радиус и высоту
Чему равен объём конуса V, если радиус его основания r, а высота h?
Формула
V = ⅓ ⋅ π ⋅ r² ⋅ h
через диаметр:
V = ⅓ ⋅ π ⋅ (d/2)² ⋅ h
Пример
Для примера посчитаем объём конуса, у которого высота h = 6 см, а радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3² ⋅ 6 = 169.56/3 = 56.52 см³
Объём конуса через угол раствора (α) и радиус
Чему равен объём конуса V, если угол раствора α, а радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³/tg (α/2)
Пример
Для примера посчитаем объём конуса, имеющего угол раствора α = 30° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³/tg(30/2) ≈ 1,0467 ⋅ 8 / 0.2679 ≈ 31.25 см³
Объём конуса через угол β и радиус
Чему равен объём конуса V, если известны угол β и радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³/tg β
Пример
Для примера посчитаем объём конуса, имеющего угол β = 20° и радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3³/tg 20 ≈ 1,0467 ⋅ 27 / 0.36397 ≈ 77.64 см³
Объём конуса через угол γ и радиус
Чему равен объём конуса V, если известны угол γ и радиус основания r?
Формула
V = ⅓ ⋅ π ⋅ r³ ⋅ tg γ
Пример
Для примера посчитаем объём конуса, имеющего угол γ = 45° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³ ⋅ tg 45 ≈ 1,0467 ⋅ 8 ⋅ 1 ≈ 8.37 см³
См. также
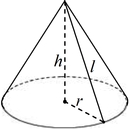
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.
Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.
Радиус конуса – это радиус его основания.
Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Формула объема конуса
Объем конуса можно вычислить, зная его высоту H и площадь основания:
V = 1/3 ⋅ Sосн ⋅ H = 1/3πR2H
Как найти объем конуса
Среди многообразия геометрических тел одним из самых интересных является конус. Образуется он путем вращения прямоугольного треугольника вокруг одного из своих катетов.
1
Как найти объем конуса – основные понятия
Перед тем, как начать вычисления объема конуса, стоит ознакомиться с основными понятиями.
- Круговой конус – основанием такого конуса является круг. Если в основании лежит эллипс, парабола или гипербола, то фигуры называются эллиптическим, параболическим или гиперболическим конусом. Стоит помнить, что два последних вида конуса имеют бесконечный объем.
- Усеченный конус – часть конуса, расположенная между основанием и плоскостью, параллельной этому основанию, находящейся между вершиной и основанием.
- Высота – перпендикулярный основанию отрезок, выпущенный из вершины.
- Образующая конуса – отрезок, соединяющий границу основания и вершину.
2
Объем конуса
Для расчета объема конуса применяется формула V=1/3*S*H, где S – площадь основания, H – высота. Так как основание конуса – круг, то его площадь находится по формуле S= nR^2, где n = 3,14, R – радиус окружности.
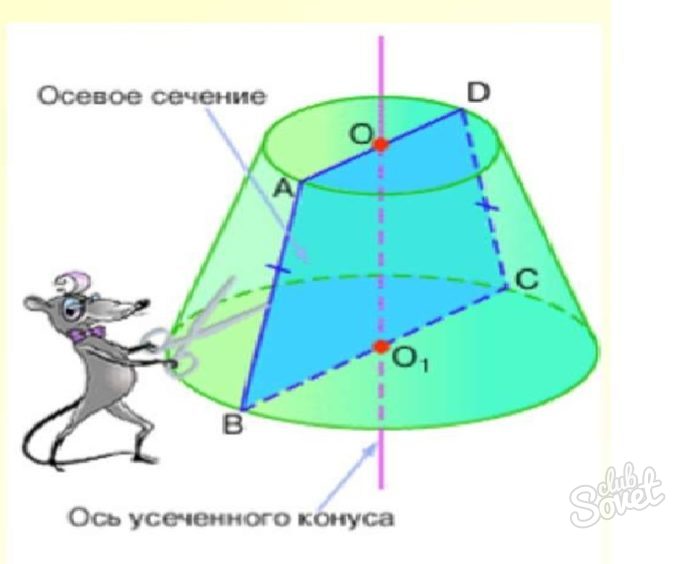
Бывает ситуация, когда неизвестны какие-то из параметров: высота, радиус или образующая. В таком случае стоит прибегнуть к теореме Пифагора. Осевым сечением конуса является равнобедренный треугольник, состоящий из двух прямоугольных треугольника, где l – гипотенуза, а H и R – катеты. Тогда l=(H^2+R^2)^1/2.
3
Объем усеченного конуса
Усеченный конус представляет собой конус с обрезанной верхушкой.
Чтобы найти объем такого конуса понадобится формула:
V=1/3*n*H*(r^2+rR+R^2),
где n=3.14, r – радиус окружности сечения, R – радиус большого основания, H – высота.
Осевым сечением усеченного конуса будет равнобедренная трапеция. Поэтому, если необходимо найти длину образующей конуса или радиуса одной из окружностей, стоит применять формулы для нахождения боковых сторон и оснований трапеции.
Пример:
Найти объем конуса, если его высота равна 8 см, радиус основания 3 см.
Дано: H=8 см, R=3 см.
Сначала найдем площадь основания, применив формулу S=nR^2.
S=3.14*3^2=28.26 см^2
Теперь по формуле V=1/3*S*H находим объем конуса.
V=1/3*28.26*8=75.36 см^3
Фигуры в форме конуса встречаются повсюду: парковочные конусы, башни строений, абажур светильника. Поэтому знание, как найти объем конуса, порой может пригодиться как в профессиональной, так и в повседневной жизни.
Типология урока: Урок общеметодологической
направленности;
Цели урока:
- Содержательная: Расширение понятийной
базы по теме конус и его элементы за счет
включения в нее новых элементов знаний: формул
для вычисления объема конуса; - Деятельностная: Формирование у студентов
умений организовывать свою учебную
деятельность, пользоваться умением
самопроверки, реализации новых способов
действий через связь с задачами математического
анализа на применение интеграла и первообразной
и умений применения новых знаний для решения
задач на вычисление объема конуса;
Базовые знания:
- Понятие конуса и его элементов;
- Вычисление площади круга через радиус и
диаметр; - Вычисление интеграла;
- Вписанные и описанные окружности;
Формы учебной работы:
- Индивидуальная, коллективная (группами и
парами);
Оборудование:
- компьютер, презентация;
- проектор;
- макеты конуса;
- рабочая карточка;
- экран;
- рабочие тетради;
Структура урока
- Мобилизационный этап.
- Целеполагание.
- Повторение опорных знаний и момент осознания
недостаточности имеющихся знаний. - Реализация проекта урока.
- Домашнее задание.
- Рефлексия.
Ход урока
1. Мобилизационный этап.
Здравствуйте, уважаемые преподаватели,
студенты! Я очень рада всех вас видеть, на моем
уроке. Уважаемые, гости, студенты! Тема нашего
открытого урока: “Объем конуса”.
Разобьемся на три команды. Задача каждой
команды – показать свои знания и приобрести
новые, взаимовыручка и отличные оценки. Интрига
сегодняшнего урока: разыгрывается домашнее
задание. Победитель его не получает.
Мы сегодня должны будем применить знания тем
прошлых уроков. В тетрадях записываем дату, номер
урока и тему занятия. И сразу вопрос: “Как
связано изображение на слайде №1и название темы
урока?” Ответ запишите в рабочую карточку
(приложение 1), где необходимо указать и ваши
инициалы. (слайды 1, 2). Немного истории: разбираем,
что оказывается “конус” – в переводе с
латыни это сосновая шишка. Разбираем примеры
конуса из жизни, подводя студентов к важности
знаний о конусе. (слайд 3-5).
2. Целеполагание.
Цели урока: Формирование умений
организовывать учебную деятельность,
пользоваться умением самопроверки, реализации
новых способов действий через связь с задачами
математического анализа на применение интеграла
и первообразной и умений применения новых знаний
для решения задач на вычисление объема конуса.
(слайд 6).
3. Повторение опорных знаний и момент осознания
недостаточности имеющихся знаний.
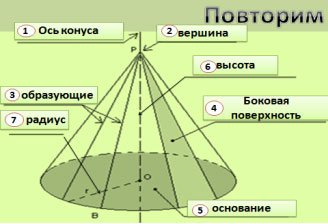
Устно разбираем чертеж конуса и повторяем его
основные элементы: (слайд 8)
- ось конуса
- вершина
- образующие
- боковая поверхность
- основание
- высота
- радиус основания
За каждый правильный ответ команды набирают
баллы.
Повторяем площадь круга через радиус и выводим
формулу площади круга через диаметр.
Закрепляем умение находить площадь круга:
решением трех заданий (каждой команде по одному
заданию) на вычисление площади круга, зная радиус
и диаметр. Работаем самостоятельно, результат
оформляем в рабочую карточку
(приложение 1). По окончании работы
проверяем, ставим оценку – балл. (слайд 9)
На слайде № 10 изображена картинка: рожок с
мороженым в виде конуса. Попробуем
сформулировать вопрос: “Если 100 мл. мороженого
стоит 100 рублей, а у нас в кармане меньше, то какую
величину необходимо высчитать, чтобы все- таки
купить мороженое?”.
4. Реализация проекта урока.
Проект дальнейшего урока разделяем на 4 этапа.
4.1. Выводим формулу вычисления объема
конуса. Применяем знания из урока по теме:
“Практическое применение интеграла и
производной”. . Вывод формулы предлагается желающему
студенту. (слайд 11,12)
4.2. Рассуждаем. (слайд 13)
Отвечаем самостоятельно на предложенные
вопросы, записываем результат в карточку (приложение 1).
1. Что необходимо измерить у конуса для
нахождения его объема?
2. Зная радиус основания и объем, что можно найти
у конуса?
3. Зная высоту и объем, что можно определить у
конуса?
4. Если известна образующая и радиус основания,
можно ли определить объем конуса?
5. С формулой, вычисления объема, какого
многогранника можно сравнить общую формулу
вычисления объема конуса?
6. Что общего и отличительного в этих формулах?
7. Формула вычисления площади круга через
радиус?
8. Формула вычисления площади круга через
диаметр?
9.Формула вычисления объема конуса?
После окончания задания команды защищают свое
право на правильный ответ, при этом набирают за
правильный ответ баллы.
Этап “Рассуждаем” я включила с целью
научить ребят рассуждать логически и уметь
систематизировать, полученные знания и делать
выводы, также с проверкой умственных
способностей к запоминанию формул, разбираемых
ранее.
4.3. Этот этап урока рассчитан на умение
студентом самому сформулировать вопрос к задаче
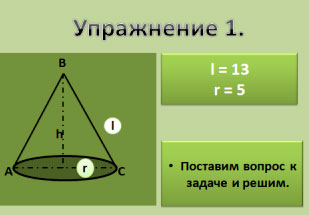
и ответить на него. Поставим вопрос к задаче
и решим, если известно, что дан конус с
образующей, равной 13 и радиусом, равным 5.
На данном этапе работы из всех предложенных
вопросов выбираются наиболее интересные,
например такие как:
– вычислить высоту конуса
– вычислит площадь основания конуса
– вычислить объем конуса
– вычислить площадь осевого сечения конуса;
Каждой команде предоставляется решить задачу,
с поставленным вопросом и объяснить свое
решение, за что команды получают балл. Результат
оформляем в рабочую карточку
(приложение 1), (слайд 14).
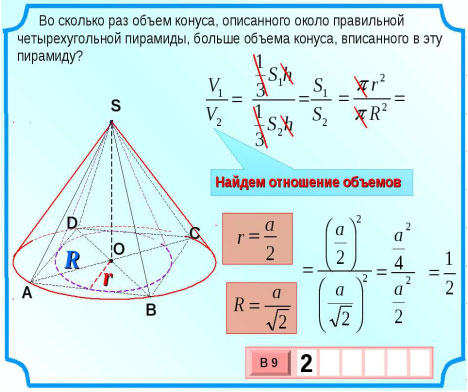
4.4. На последнем этапе рассмотрим
вариативную задачу: (слайд 15)
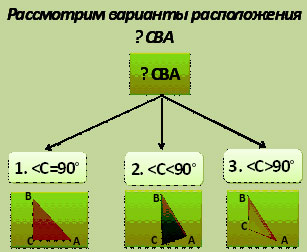
Условие: Доказать, что если треугольник
АВС вращать вокруг стороны ВС = а, то V полученного
тела можно вычислить по формуле: , где Q – площадь
треугольника АВС.
Здесь необходим при анализе задачи перебор
вариантов, то есть надо рассмотреть каким может
быть угол С, прилежащий к стороне ВС. Тут три
варианта: угол прямой, угол острый и угол тупой,
по варианту для команды. (слайд 16-20).
Вырабатываем общую стратегию решения:
1. Определим полученное геометрическое тело.
2. Определим, из каких тел складывается
полученное геометрическое тело?
V = ?
1 случай (треугольник прямоугольный):
2 случай (треугольник остроугольный):
3 случай (треугольник тупоугольный):
3. Из формулы, вычисления площади треугольника:
“Площадь треугольника равна половине
произведения основания на высоту, проведенную к
этому основанию”, определим r и r2: ;
4. Подставим r2 в формулу объема V.
;
5. Формула доказана.
Разбираем и решаем. Результат заносим в рабочую
карту (приложение 1).
5. Домашнее задание. (слайд 21)
6. Рефлексия.
Подведем итоги и попытаемся ответить
на вопросы: (слайд 22)
1. Что означает “конус”?
2. Площадь круга через r?
3. Площадь круга через d?
4. Объем конуса?
5. Какие задания вызвали затруднения, а какие
нет?
Ваша оценка уроку?
Соответственно из подсчитанных балов
формируется оценка работавшим студентам на
уроке.
- “5” получают студенты из команды, занявшей
первое место. - “4” получают студенты, занявшие второе и третье
места.