Как найти объем конуса если увеличить основание - Сайт, где вы сможете решить свои вопросы

Определение конуса

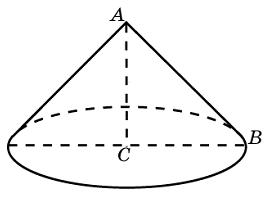
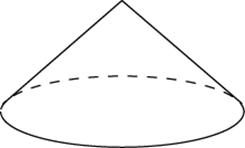
Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.

Онлайн-калькулятор объема конуса

Общее определение конуса

Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.

Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.

Рассмотрим некоторые важные понятия.

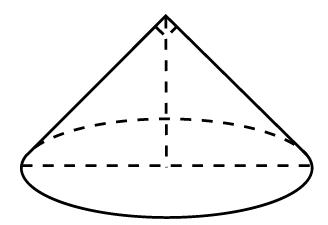
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.

Конус бывает нескольких типов:

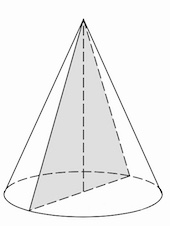
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.

Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.

Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.

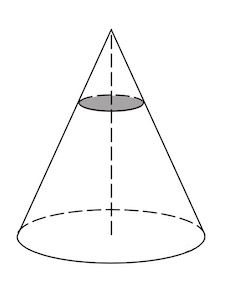
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.

Формула объема прямого конуса

Объем прямого конуса можно рассчитать по следующей формуле:

V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h

где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.

Рассмотрим несколько примеров.

Задача 1

Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.

Решение

l=5l=5
R=3R=3

Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:

l2=h2+R2l^2=h^2+R^2

Отсюда, hh:

h=l2−R2h=sqrt{l^2-R^2}

h=52−32h=sqrt{5^2-3^2}

h=25−9h=sqrt{25-9}

h=16h=sqrt{16}

h=4h=4

Затем находим площадь основания конуса. Это площадь круга радиуса RR:

Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26

Последние вычисления — нахождение объема конуса по формуле:

V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3

Ответ: 37.68 см3.37.68text{ см}^3.

Задача 2

Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.

Решение

D=8D=8
h=9h=9

Найдем радиус RR круга через его диаметр:

R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4

Площадь этого круга и есть основание нашего конуса:

Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24

Сам объем равен:

V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3

Ответ: 150.72 см3.150.72text{ см}^3.

Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!

Тест на тему “Объем конуса”

Источник

Версия для печати и копирования в MS Word

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 22 раза, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 17 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 26 раз, а высота останется прежней?

Во сколько раз увеличится объём конуса, если радиус его основания увеличится в 4 раза, а высота останется прежней?

Во сколько раз увеличится объём конуса, если радиус его основания увеличится в 3 раза, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 40 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 14 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 4,5 раза, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 3 раза, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 9 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 33 раза, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 30 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 27 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 15 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 41 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 36 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 39 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 13 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 11 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 25 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 32 раза, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 16 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 38 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 31 раз, а высота останется прежней?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 45 раз, а высота останется прежней?

Источник

Здравствуйте, Дорогие друзья! В этой статье рассмотрим пару задач, в которых речь идёт об объёме конуса. В прошлой статье мы уже рассмотрели несколько заданий. Суть простая – стоит условие об уменьшении (увеличении) высоты конуса или радиуса в определённое. Ставится вопрос о том, как изменился объём. Ещё раз формула объёма конуса:

Сначала рассмотрим задачи, а затем изложу пару рекомендаций к решению.

27094. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?

Объём конуса:

Очевидно, что если мы уменьшим высоту в три раза, то объём уменьшиться также в три раза (зависимость прямолинейная). Формально это можно записать так:

Ответ: 3

27095. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?

Объём конуса:

Увеличим радиус в 1,5 раза:

Объём увеличится в 2,25 раза.

Ответ: 2,25

*То есть можно сделать вывод:

Если радиус основания конуса изменить (увеличить или уменьшить) в n раз, то его объём соответственно увеличится или уменьшится в n² раз. Посмотрите формальную запись:

Поставим такую задачу. Как изменится объём конуса, если его высоту увеличить в 10 раз, а радиус уменьшить в 4 раза.

Объём конуса равен:

Увеличим высоту в 10 раз и уменьшим радиус в 4:

По величине 0,625 видно, что объём уменьшится. То есть объём полученного конуса составит 0,625 от объёма исходного конуса.

Ещё это изменение можно выразить следующим образом.

Объём исходного конуса разделить на объём полученного и определить во сколько раз произойдёт уменьшение:

То есть объём конуса уменьшится в 1,6 раза.

Можно сказать так – объём полученного конуса в 1,6 меньше исходного.

Небольшой итог!

Как видите, задачи очень простые. Суть процесса решения сводится к тому, чтобы формулу объёма полученного конуса «привести» к такому виду:

*То есть, чтобы полученный объём выражался через объём исходного конуса.

Разумеется, если будет идти речь только об изменении высоты, то такую задачу можно решить устно (прямая зависимость).

Вторую задачу (где изменяется только радиус) при наличии опыта тоже можно решить устно, но лучше подробно записать процесс вычисления.

Задач, где речь идёт об изменении обеих величин на экзамене не предполагается, но будьте готовы на всякий случай.

В будущем обязательно рассмотрим приём, которым очень удобно пользоваться при решении подобных заданий. Речь пойдёт не только о конусах, но и о других телах, не пропустите, подпишитесь на рассылку.

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Скачать материал

без ожидания

Скачать материал

без ожидания

Сейчас обучается 140 человек из 50 регионов

Сейчас обучается 176 человек из 50 регионов

Описание презентации по отдельным слайдам:

1 слайд

Задачи по теме Конус
2 слайд

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 9, а второго — 6 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?

Решение: Т.к. площадь боковой поверхности конуса: S=πrl.
Значит S1= π·3·9= 27π,
S2= π·6·9= 54π, тогда S2: S1= 54π : 27π = 2
3 слайд

1) Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого? Ответ: 6
Решить самостоятельно
4 слайд

Объём конуса равен 160., Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Решение:
Отношение объемов конусов равно кубу их коэффициента подобия. Высоты конусов относятся как 1:2, поэтому их объемы относятся как 1:8.
Следовательно, объем отсекаемого конуса равен 160 : 8 = 20
5 слайд

Решить самостоятельно
Объём конуса равен 135. Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью. Ответ:5
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Ответ:2
Объем конуса равен 128. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Ответ:16
6 слайд

Объём конуса равен 150π а его высота равна 6 . Найдите радиус основания конуса.
Решение: Найдём радиус основания конуса по формуле: V=1/3·πR²h
Откуда R²=3V:πh => R²= 150π : 6π = 25. Тогда R=5
7 слайд

Решить самостоятельно
Объём конуса равен 9π, а его высота равна 3 . Найдите радиус основания конуса. Ответ:3
Объём конуса равен 25π, а его высота равна 3 . Найдите радиус основания конуса. Ответ:5
8 слайд

Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?
Решение: Объем конуса вычисляется по формуле V=1/3·Socн·h .
Значит, если высоту уменьшить в 3 раза, то и объём уменьшится в 3 раза
9 слайд

Решить самостоятельно
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 18,5 раза?
2) Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 24 раза?
3) Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 10 раз?
10 слайд

Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
Решение: Объем конуса вычисляется по формуле
V=1/3·Soc.·h = 1/3·πR²·h.
Значит, если радиус основания увеличить в 1,5 раза, то объём конуса увеличится в 2,25 раза
11 слайд

Решить самостоятельно
Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 40 раз?
2) Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 22 раза?
3) Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 31 раз?
12 слайд

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
Решение: Площадь боковой поверхности конуса вычисляется по формуле
S= πR·L, где L-образующая.
Значит если увеличить L в 3 раза, то площадь боковой поверхности конуса тоже увеличится в 3 раза.
13 слайд

Решить самостоятельно
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз?
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 11 раз?
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 1,5 раза?
14 слайд

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?

Решение: Площадь боковой поверхности конуса вычисляется по формуле S= πR·L.
Значит, если радиус основания уменьшится в 1,5 раза, то площадь боковой поверхности конуса тоже уменьшится в 1,5 раза.
15 слайд

Решить самостоятельно
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 8 раз, а образующая останется прежней?
2) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 36 раз, а образующая останется прежней?
3) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 21 раз, а образующая останется прежней?
16 слайд

Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Решение: По теореме Пифагора
𝑳= 𝑯 𝟐 + 𝒅 𝟐 𝟐 = 𝟏𝟔+ 𝟑𝟔 𝟒 = 𝟐𝟓 =𝟓
17 слайд

Решить самостоятельно
Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса. Ответ: 17
2) Высота конуса равна 5, а диаметр основания — 24. Найдите образующую конуса. Ответ: 13
3) Высота конуса равна 6, а диаметр основания — 16. Найдите образующую конуса. Ответ: 10
18 слайд

Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Решение: По теореме Пифагора
𝑹= 𝑳 𝟐 − 𝑯 𝟐 = 𝟐𝟓−𝟏𝟔 = 𝟗 =3;
2R = 6
19 слайд

Решить самостоятельно
Высота конуса равна 72, а длина образующей — 90. Найдите диаметр основания конуса.
Ответ:108
2) Высота конуса равна 21, а длина образующей — 75. Найдите диаметр основания конуса. Ответ: 54

3) Высота конуса равна 57, а длина образующей — 95. Найдите диаметр основания конуса. Ответ: 76
20 слайд

Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
Решение: По теореме Пифагора
𝑯= 𝑳 𝟐 − 𝒅 𝟐 𝟐 = 𝟐𝟓− 𝟑𝟔 𝟒 = 𝟏𝟔 =𝟒;
21 слайд

Решить самостоятельно
Диаметр основания конуса равен 108, а длина образующей — 90. Найдите высоту конуса. Ответ: 72
2) Диаметр основания конуса равен 42, а длина образующей — 75. Найдите высоту конуса. Ответ: 72
3) Диаметр основания конуса равен 24, а длина образующей — 13. Найдите высоту конуса. Ответ: 5
22 слайд

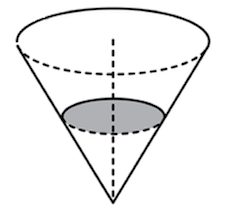
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение: Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 70 ∙ 8 = 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости.
23 слайд

В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
Решение: Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса. Объем налитой жидкости равен 1600 : 8 = 200 мл.
24 слайд

Решить самостоятельно
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/3 высоты. Объём жидкости равен 14 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Ответ: 364
2) В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 40 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Ответ: 280
3) В сосуде, имеющем форму конуса, уровень жидкости достигает 1/4 высоты. Сколько миллилитров жидкости налито в сосуд, если объем всего сосуда равен 384? Ответ: 6
25 слайд

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 𝟑 𝟐 . Найдите площадь боковой поверхности конуса.
Решение: Так как цилиндр имеет высоту, равную радиусу основания, то площадь боковой поверхности цилиндра равна 𝑺 бц =𝟐𝝅𝑹𝑯=𝟐𝝅 𝑹 𝟐 =𝟑 𝟐 , следовательно

𝝅 𝑹 𝟐 = 𝟑 𝟐 𝟐

Площадь боковой поверхности конуса равна
𝑺 бк =𝝅𝑹𝑳, так как 𝑳= 𝑯 𝟐 + 𝑹 𝟐 = 𝟐 𝑹 𝟐 =𝑹 𝟐 ;

𝑺 бк =𝝅𝑹𝑳=𝝅𝑹∙𝑹 𝟐 = 𝟐 𝝅 𝑹 𝟐 = 𝟑 𝟐 𝟐 ∙ 𝟐 =𝟑
26 слайд

Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Решение: Осевым сечением конуса является равнобедренный треугольник, основание которого —это диаметр основания конуса, а высота совпадает с высотой конуса. Так как R = 6, то
𝑯= 𝑳 𝟐 − 𝑹 𝟐 = 𝟏𝟎𝟎−𝟑𝟔 =𝟖;
Следовательно, площадь осевого сечения
𝑺 сеч = 𝟏 𝟐 ∙𝑯∙𝟐𝑹= 𝟏 𝟐 ∙𝟖∙𝟏𝟐=𝟒𝟖
27 слайд

1) Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса. Ответ: 48
Решить самостоятельно
28 слайд

Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью
Решение: Сечение плоскостью, параллельной основанию, представляет собой круг, радиус которого относится к радиусу основания конуса как 3 : 9. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому площадь сечения в 9 раз меньше площади основания. Тем самым, она равна 2.
29 слайд

Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.
Решение: Осевым сечением конуса является равнобедренный треугольник, высота которого совпадает с высотой конуса, а основание является диаметром основания конуса. Поэтому площадь осевого сечения равна половине произведения высоты конуса на диаметр его основания или произведению высоты конуса на радиус основания R. Поскольку по условию πR²=16π, то радиус основания конуса равен 4, а тогда искомая площадь осевого сечения равна 24.
30 слайд

Решить самостоятельно
Площадь основания конуса равна 36π, высота —10. Найдите площадь осевого сечения конуса. Ответ:60
31 слайд

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 𝟏𝟎 𝟐 . Найдите образующую конуса.
Решение: Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем:

𝑳= 𝑹 𝟐 + 𝑹 𝟐 =𝑹 𝟐 ;

𝑳=𝟏𝟎 𝟐 ∙ 𝟐 =𝟐𝟎
32 слайд

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Решение: Формулу для объёма шара: 𝑽= 𝟒 𝟑 𝝅 𝑹 𝟑 , а формула объёма конуса: 𝑽= 𝟏 𝟑 𝝅 𝑹 𝟑 .
Значит объём конуса в 4 раза меньше объёма шара. Тогда объём конуса равен V = 28 : 4 = 7
33 слайд

Решить самостоятельно
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 116. Найдите объем конуса. Ответ: 29
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 160. Найдите объем конуса. Ответ: 40
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 132. Найдите объем конуса. Ответ: 33
34 слайд

Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение: 𝑺 бок =𝟐 𝑺 осн ; 𝝅𝑹𝑳=𝟐𝝅 𝑹 𝟐 ;
𝑳=𝟐𝑹
Значит, в прямоугольном треугольнике, образованном высотой, образующей и радиусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Следовательно, угол между образующей конуса и плоскостью основания равен 60°.
35 слайд

Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π .
Решение: По теореме Пифагора
𝑳= 𝑯 𝟐 + 𝑹 𝟐 = 𝟏𝟔+𝟗 = 𝟐𝟓 =𝟓;
Площадь полной поверхности конуса

𝑺=𝝅 𝑹 𝟐 +𝝅𝑹𝑳=𝝅𝑹 𝑳+𝑹 =𝝅∙𝟑∙𝟖=𝟐𝟒𝝅;
𝑺 𝝅 =𝟐𝟒
36 слайд

Решить самостоятельно
Радиус основания конуса равен 12, высота равна 16. Найдите площадь полной поверхности конуса, деленную на π . Ответ: 264
2) Радиус основания конуса равен 28, высота равна 21. Найдите площадь полной поверхности конуса, деленную на π . Ответ: 1764
3) Радиус основания конуса равен 15, высота равна 36. Найдите площадь полной поверхности конуса, деленную на π . Ответ: 810
37 слайд

Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Решение: Длина окружности: 𝑪=𝟐𝝅𝑹=𝟑;
𝝅𝑹= 𝟑 𝟐
Площадь боковой поверхности конуса 𝑺=𝝅𝑹𝑳= 𝟑 𝟐 ∙𝟐=𝟑
38 слайд

Решить самостоятельно
Длина окружности основания конуса равна 6, образующая равна 2. Найдите площадь боковой поверхности конуса. Ответ: 6
Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса. Ответ: 20
Длина окружности основания конуса равна 8, образующая равна 6. Найдите площадь боковой поверхности конуса. Ответ: 24
39 слайд

Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного H = 6. Найдите объем конуса, деленный на π .
Решение: Радиус основания равен высоте конуса и равен 6, тогда объем конуса равен:
𝑽= 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟏 𝟑 𝝅 𝑹 𝟑 = 𝟏 𝟑 𝝅∙ 𝟔 𝟑 =𝟕𝟐𝝅;

𝑽 𝝅 = 𝟕𝟐𝝅 𝝅 =𝟕𝟐
40 слайд

Решить самостоятельно
Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 15. Найдите его объем, деленный на π . Ответ: 1125
2) Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 120. Найдите его объем, деленный на π . Ответ: 576000
3) Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 60. Найдите его объем, деленный на π . Ответ: 72000
41 слайд

Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
Решение: В равнобедренном прямоугольном треугольнике высота, проведенная из вершины прямого угла равна половине гипотенузы, т.е. радиусу основания конуса: H = R = 3. Тогда объем конуса вычисляется следующим образом:
𝑽= 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟏 𝟑 𝝅 𝑹 𝟑 = 𝟏 𝟑 𝝅∙ 𝟑 𝟑 =𝟗𝝅;

𝑽 𝝅 = 𝟗𝝅 𝝅 =𝟗
42 слайд

Решить самостоятельно
Диаметр основания конуса равен 66, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
Ответ: 11979
Диаметр основания конуса равен 12, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
Ответ: 72
Диаметр основания конуса равен 36, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
Ответ: 1944
43 слайд

Найдите объем конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30° . В ответе укажите V/π.
Решение: Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в 30° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. H = 1
Радиус основания найдем по теореме Пифагора: 𝑹= 𝑳 𝟐 − 𝑯 𝟐 = 𝟒−𝟏 = 𝟑
𝑽= 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟏 𝟑 𝝅∙ 𝟑 𝟐 ∙𝟏=𝝅;

𝑽 𝝅 = 𝝅 𝝅 =𝟏
44 слайд

Решить самостоятельно
Найдите объем конуса, образующая которого равна 44 и наклонена к плоскости основания под углом 30° . В ответе укажите V/π. Ответ: 10 648
Найдите объем конуса, образующая которого равна 52 и наклонена к плоскости основания под углом 30° . В ответе укажите V/π. Ответ: 17576
Найдите объем конуса, образующая которого равна 34 и наклонена к плоскости основания под углом 30° . В ответе укажите V/π. Ответ: 4913
45 слайд

Решение: Радиус основания конуса R равен половине диагонали квадрата ABCD:
𝑹= 𝟏 𝟐 𝑨𝑪= 𝟏 𝟐 ∙𝟒 𝟐 =𝟐 𝟐
Тогда объем конуса равен:
𝑽= 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟏 𝟑 𝝅 𝟐 𝟐 𝟐 ∙𝟔=𝟏𝟔𝝅;

𝑽 𝝅 = 𝟏𝟔𝝅 𝝅 =𝟏𝟔
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.
46 слайд

Решить самостоятельно
Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 13. Найдите его объем, деленный на π. Ответ: 19,5
Конус описан около правильной четырехугольной пирамиды со стороной основания 8 и высотой 12. Найдите его объем, деленный на π. Ответ: 128
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 9. Найдите его объем, деленный на π. Ответ: 24
47 слайд

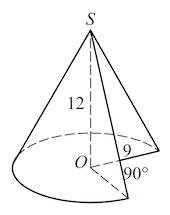
Решение: Объем данной части конуса равен

𝑽= 𝟗𝟎° 𝟑𝟔𝟎° ∙ 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟏 𝟒 ∙ 𝟏 𝟑 𝝅∙ 𝟗 𝟐 ∙𝟏𝟐=𝟖𝟏𝝅;

𝑽 𝝅 = 𝟖𝟏𝝅 𝝅 =𝟖𝟏
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .
S
90°
12
9
48 слайд

Решить самостоятельно
1) Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .

S
90°
14
6
S
90°
18
12
S
90°
24
9
Ответ: 126
Ответ: 486
Ответ: 648
49 слайд

Решение: Объем данной части конуса равен

𝑽= 𝟔𝟎° 𝟑𝟔𝟎° ∙ 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟏 𝟔 ∙ 𝟏 𝟑 𝝅∙ 𝟏𝟐 𝟐 ∙𝟐𝟕=𝟐𝟏𝟔𝝅;

𝑽 𝝅 = 𝟐𝟏𝟔𝝅 𝝅 =𝟐𝟏𝟔
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .
S
60°
27
12
50 слайд

Решить самостоятельно
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .

S
60°
21
12
S
60°
33
12
S
60°
36
18
Ответ: 504
Ответ: 1944
Ответ: 792
51 слайд

Решение: Объем данной части конуса равен

𝑽= 𝟐𝟕𝟎° 𝟑𝟔𝟎° ∙ 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟑 𝟒 ∙ 𝟏 𝟑 𝝅∙ 𝟏𝟐 𝟐 ∙𝟏𝟓=𝟓𝟒𝟎𝝅;

𝑽 𝝅 = 𝟓𝟒𝟎𝝅 𝝅 =𝟓𝟒𝟎
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .
O
S
90°
15
12
52 слайд

Решить самостоятельно
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .
O
S
90°
14
12
O
S
90°
13
6
O
S
90°
12
9
Ответ: 504
Ответ: 117
Ответ: 243
53 слайд

Решение: Объем данной части конуса равен

𝑽= 𝟑𝟎𝟎° 𝟑𝟔𝟎° ∙ 𝟏 𝟑 𝝅 𝑹 𝟐 𝑯= 𝟓 𝟔 ∙ 𝟏 𝟑 𝝅∙ 𝟗 𝟐 ∙𝟐𝟕=𝟏𝟖𝟐𝟐,𝟓𝝅;

𝑽 𝝅 = 𝟏𝟖𝟐𝟐,𝟓𝝅 𝝅 =𝟏𝟖𝟐𝟐,𝟓
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .
O
S
60°
27
9
54 слайд

Решить самостоятельно
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π .
O
S
60°
14
12
O
S
60°
13
6
O
S
60°
11
9
Ответ: 1680
Ответ: 390
Ответ: 742,5

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 257 271 материал в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

Контрольная работа по геометрии 10 класс

Учебник: «Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
Тема: § 3. Двугранный угол. Перпендикулярность плоскостей

28.03.2018
822
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
Курс повышения квалификации «Основы построения коммуникаций в организации»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Основы менеджмента в туризме»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
Курс профессиональной переподготовки «Организация маркетинговой деятельности»
Курс профессиональной переподготовки «Стандартизация и метрология»

Источник

09
Сен 2013

Категория: 02 Стереометрия

02. Конус

2013-09-09
2022-09-11

Задача 1. Высота конуса равна , образующая равна Найдите его объем, деленный на .

Решение: + показать

Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного Найдите его объем, деленный на .

Решение: + показать

Задача 3. Высота конуса равна а диаметр основания – Найдите образующую конуса.

Решение: + показать

Задача 4. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом В ответе укажите $frac{V}{pi}.$

Решение: + показать

Задача 5. Длина окружности основания конуса равна образующая равна Найдите площадь боковой поверхности конуса.

Решение: + показать

Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?

Решение: + показать

Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в раз?

Решение: + показать

Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в раз, а высота останется прежней?

Решение: + показать

Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Решение: + показать

Задача 10. Объем конуса равен Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решение: + показать

Задача 11. Площадь полной поверхности конуса равна Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Решение: + показать

Задача 12. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом $30^{circ}.$ В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 13. Диаметр основания конуса равен а угол при вершине осевого сечения равен °. Вычислите объем конуса, деленный на .

Решение: + показать

Задача 14. Площадь основания конуса равна , высота — Найдите площадь осевого сечения конуса.

Решение: + показать

Задача 15. Площадь основания конуса равна Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной и считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Решение: + показать

Задача 16. Найдите объем части конуса, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 17. Найдите объем части конуса, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает $frac{1}{2}$ высоты. Объём жидкости равен мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?