В этой статье для вас представлены задачи по стереометрии с комбинацией тел – правильной четырёхугольной пирамидой и конусом, который около неё описан (или вписан в неё). Ставятся вопросы о вычислении объёма.
Необходимая теория: формула объёма конуса, теорема Пифагора. Понятно, что если речь идёт о конусе, который описан или вписан в пирамиду, то их высоты будут равны (высота у них общая). Объём конуса:
Рассмотрим задачи:
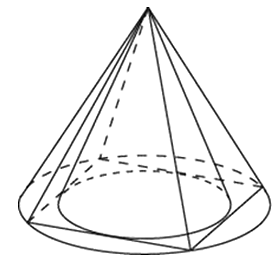
Конус описан около правильной четырехугольной пирамиды со стороной основания 12 и высотой 10. Найдите его объем, деленный на Пи.
Объём конуса равен произведению одной трети его основания и высоты:
Высота нам известна, необходимо найти радиус основания конуса. Он равен половине диагонали квадрата ABCD. По теореме Пифагора мы можем её вычислить:
Значит радиус основания конуса будет равен:
Таким образом, объем конуса:
Результат разделим на Пи и запишем ответ.
Ответ: 240
Объём конуса, описанного около правильной четырёхугольной пирамиды, равен 64. Найдите объём конуса, вписанного в эту пирамиду.
Объём конуса равен произведению одной трети площади его основания и высоты:
Высоты конусов равны. Получается, что единственная величина от которой зависят объёмы конусов это площади их оснований. Если мы определим как они взаимосвязаны, то тогда без труда ответим на поставленный вопрос.
Пусть радиус основания вписанного конуса равен r. Тогда площадь основания вписанного конуса равна:
Радиус основания описанного конуса будет равен:
*Подробнее о связи радиусов вписанной и описанной около квадрата окружности можете посмотреть информацию здесь.
Мы получили, что площадь основания описанного конуса в 2 раза больше площади основания вписанного конуса.
Вывод: объём конуса описанного около правильной четырёхугольной пирамиды будет в 2 раза больше объёма вписанного конуса.
Таким образом, объём конуса вписанного в пирамиду будет равен 32.
Разберём второй подход к решению:
Нам известен объём описанного конуса, нет никаких других данных. Необходимо установить как взаимосвязаны объёмы конусов.
Обозначим сторону квадрата в основании пирамиды как а, запишем чему будет равен объём вписанного конуса:
Диаметр основания описанного конуса – это диагональ квадрата. По теореме Пифагора она будет равна:
Значит объем описанного конуса будет равен:
Найдём отношение объёмов:
Таким образом, объем описанного конуса больше объема вписанного конуса в 2 раза, и исходя из условия искомый объём будет равен 32.
Ответ: 32
27123. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на Пи.
Посмотреть решение
27124. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Делитесь информацией в социальных сетях.
Чтобы найти объем конуса необходимо произвести дополнительные построения.
Построим вписанную в конус правильную n-угольную пирамиду и опишем вокруг данного конуса правильную n-угольную пирамиду.
Вписанная пирамида содержится в конусе. Из этого следует, что ее объем не больше объема конуса.
Описанная пирамида содержит конус, а это значит, что ее объем не меньше объема конуса.
Впишем в основание вписанной пирамиды окружность.
Если радиус вписанного правильного n-угольника равен R, то радиус вписанной в него окружности будет равен:
Объем вписанной пирамиды вычисляется по формуле:
где S – основание пирамиды.
Площадь данного круга вычисляется по формуле:
Площадь основания вписанной пирамиды не меньше площади круга, содержащегося в ней
Поэтому утверждение, что объем вписанной в конус пирамиды не меньше 
А следовательно, мы может утверждать, что объем конуса, содержащий эту пирамиду будет больше или равен
V≥
Теперь опишем окружность вокруг основания описанной вокруг конуса пирамиды.
Радиус этой окружности будет равен:
Площадь данного круга вычисляется по формуле:
Основание описанной пирамиды содержится в круге описанном вокруг него. Поэтому площадь основания пирамиды не больше
Поэтому утверждение,что объем описанной пирамиды не больше 
А следовательно, мы может утверждать, что объем конуса, содержащий в эту пирамиду будет меньше или равен
Два полученных неравенства равны при любом n. Если 
Тогда из первого неравенства следует, что V≥
Из второго неравенства
Отсюда следует, что
Объем конуса равен одной трети произведения радиуса на высоту.
Пример расчета объема конуса
Найти объем конуса, если его радиус основания равен 3 см, а образующая 5 см.
Объем конуса вычисляется по формуле:
Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и радиус основания образуют прямоугольный треугольник. Воспользовавшись теоремой Пифагора имеем:
Отсюда:
Подставим значение радиуса и высоты в формулу объема конуса.
Имеем:
Как найти объём конуса, вписанного в пирамиду?
Чёрная Кнопка
Мудрец
(13032),
на голосовании
10 лет назад
Двугранный угол при основании правильной четырехугольной пирамиды равен α. Высота пирамиды равна H. Найдите объем конуса, вписанного в пирамиду.
Дополнен 10 лет назад
Помогите пожалуйста с решением
Голосование за лучший ответ
Ирина Тонина
Профи
(523)
10 лет назад
объем равен 1/3*пи*р^2*Н (Н-извесна) , нужно найти радиус р.
Найдем половину диагонали квадрата: д=Н/танг альфа
по теореме пифагора находим сторону квадрата
а^2+а^2=(2Н/танг альфа) ^2
а=Н*кор из 2/танг альфа
радиус вписанной окружности равен половине стороны а! все, подставляй и готово!
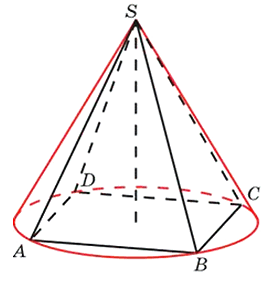
Конус вписан в пирамиду, если его основание вписано в основание пирамиды, а вершина совпадает с вершиной пирамиды. Соответственно, в этом случае пирамида описана около конуса.
Конус может быть вписан в пирамиду, если основание пирамиды — многоугольник, в который можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности. Другой вариант: конус можно вписать в пирамиду, если высоты ее боковых граней равны между собой. Отсюда, в частности, следует, что в любую правильную пирамиду можно вписать конус.
Каждая из плоскостей, содержащих боковую грань описанной пирамиды, является касательной к конусу плоскостью (то есть плоскостью, проходящей через образующую конуса перпендикулярно осевому сечению конуса, проведенному через эту образующую). Высоты боковых граней пирамиды есть образующие конуса. Высота вписанного конуса совпадает с высотой пирамиды. Радиус конуса равен радиусу вписанной в основание пирамиды окружности.
Найдем отношение объема вписанного конуса к объему пирамиды:
В частности, отношение объема вписанного конуса к объему правильной пирамиды для правильной треугольной пирамиды равно
для правильной четырехугольной пирамиды —
для правильной шестиугольной пирамиды —
(Формулу площади правильного треугольника и формулу площади правильного шестиугольника легко запомнить с помощью ассоциаций).
Теперь найдем отношение площади боковой поверхности вписанного конуса к боковой поверхности правильной пирамиды. Так как апофема пирамиды m равна образующей конуса l, имеем:
В частности, отношение боковой поверхности вписанного конуса к боковой поверхности правильной треугольной пирамиды
для правильной четырехугольной пирамиды —
для правильной шестиугольной пирамиды —
Ответ:
Объем конуса равен 576√3π см³.
Объяснение:
Конус вписан в пирамиду, значит его радиус – радиус окружности, вписанной в основание пирамиды. Высота равна высоте пирамиды.
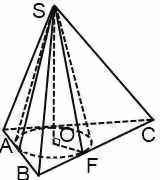
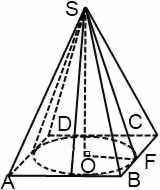
Проведем SO – высоту пирамиды.
Из точки О проведем перпендикуляры к сторонам ромба:
OK⊥AB, OL⊥BC, OM⊥CD, ON⊥AD.
Эти отрезки – проекции наклонных SK, SL, SM и SN на плоскость основания, тогда наклонные перпендикулярны сторонам ромба по теореме о трех перпендикулярах.
Значит, ∠SKO = ∠SLO = ∠SMO = ∠SNO = 60° – линейные углы двугранных углов наклона боковых граней к плоскости основания.
ΔSKO = ΔSLO = ΔSMO = ΔSNO по катету и противолежащему острому углу:
- треугольники прямоугольные, так как SO высота пирамиды;
- SO – общий катет;
- противолежащий угол 60°.
Тогда OK = OL = OM = ON, то есть точка О равноудалена от сторон ромба, значит О – центр окружности, вписанной в ромб – точка пересечения диагоналей ромба.
- Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.
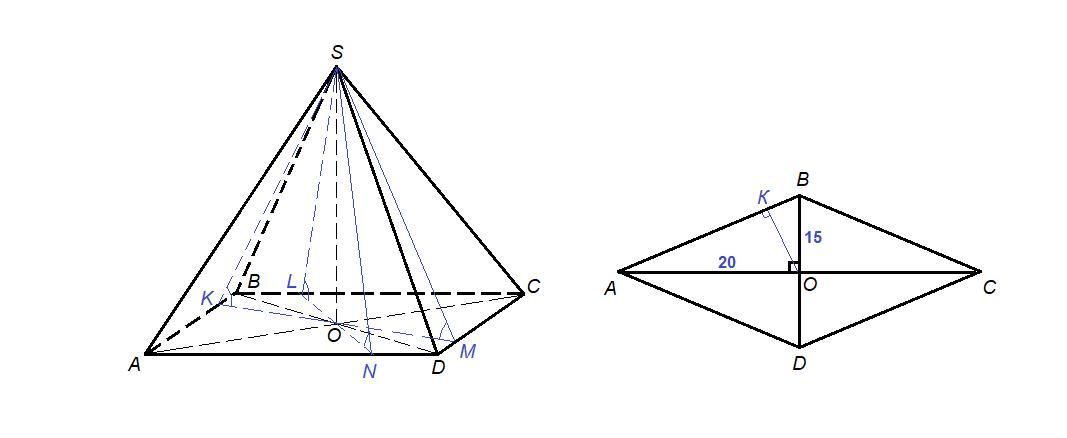
АО = 0,5 АС = 20 см
ВО = 0,5 BD = 15 см
ΔАОВ: ∠АОВ = 90°, по теореме Пифагора
АВ = √(АО² + ВО²) = √(20² + 15²) = √(400 + 225) = √625 = 25 см
ОК – высота прямоугольного треугольника, значит
OK = 12 см
ΔSOK: ∠SOK = 90°,
SO = 12√3 см
Итак, радиус основания конуса:
R = OK = 12 см
Высота:
h = SO = 12√3 см
Объем конуса:
V = 576√3π см³
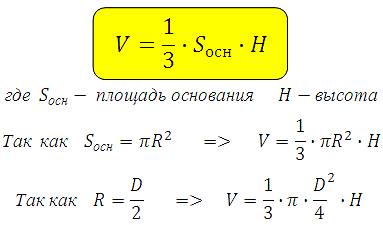

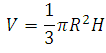
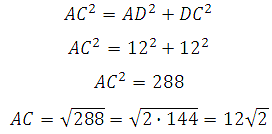
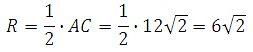
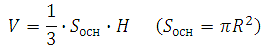
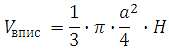
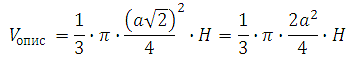
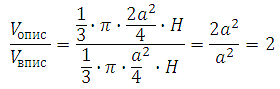


















![Rendered by QuickLaTeX.com [frac{{{V_k}}}{{{V_n}}} = frac{{pi {{(frac{a}{{2sqrt 3 }})}^2}}}{{frac{{{a^2}sqrt 3 }}{4}}} = frac{{4pi {a^2}}}{{12sqrt 3 {a^2}}} = frac{pi }{{3sqrt 3 }},]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-76cab72674870293f9e38d31ac9ac2e2_l3.png)
![Rendered by QuickLaTeX.com [frac{{{V_k}}}{{{V_n}}} = frac{{pi {{(frac{{asqrt 3 }}{2})}^2}}}{{frac{{3{a^2}sqrt 3 }}{2}}} = frac{pi }{{2sqrt 3 }}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-33cb683aba61338a176d27283f2fbd2f_l3.png)
![Rendered by QuickLaTeX.com [frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = frac{{pi cdot frac{{asqrt 3 }}{2}}}{{3a}} = frac{pi }{{2sqrt 3 }}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-a4393cd5dfc80fea40b6d86ec301e09b_l3.png)
